一種基于多維交替方向乘子法的多輸入多輸出逆合成孔徑雷達成像方法
鄧理康 張雙輝張 弛 劉永祥
(國防科技大學電子科學學院 長沙 410073)
1 引言
逆合成孔徑雷達(Inverse Syntheic Aperture Radar,ISAR)可以生成目標的二維圖像,通常用于目標識別和分類[1,2]。與二維圖像相比,三維圖像能夠獲得更多的目標信息,更便于目標識別。因此,近年來得到了越來越多學者的關注。文獻[3]研究了干涉逆合成孔徑雷達(Interferometric Inverse Synthetic Aperture Radar,InISAR)技術提取目標三維特征,但是需要面臨復雜的運動補償問題。文獻[4]提出了多輸入多輸出(Multiple-Input Multiple-Output,MIMO)的三維成像方法,該方法采用十字交叉陣列分別獲得2個維度的分辨,發射寬帶雷達信號獲得距離分辨,因此可以在單次快拍下獲得三維圖像從而避免了運動補償。但是需要的陣元數量大,硬件成本高。文獻[5]采用窄帶MIMO雷達獲得三維圖像,陣型采用接收面陣和發射線陣的設計,發射窄帶信號對目標進行單次快拍成像。但是為了獲得高分辨的三維圖像,需要的陣元數較多。文獻[6]將ISAR技術與MIMO雷達相結合,在有限成像時間內,能夠提高圖像分辨率,并且用時間采樣替代空間采樣,降低了硬件成本。但是以上方法面臨的共同特點就是需處理的數據量大,實現的硬件成本高,因此需要一種通過有限數據和硬件就能得到高分辨圖像的方法。
壓縮感知(Compressed Sensing,CS)理論[7–8]利用圖像的稀疏性,用少量采樣數據就能恢復出高分辨圖像。因此,在圖像處理領域獲得了廣泛應用。文獻[9]利用克羅內克壓縮感知(Kronecker Compressed Sensing,KCS)方法構建感知矩陣,并將多維信號轉化為一維向量,從而實現了從多維CS到一維CS的轉換。然而KCS存在的問題是測量矩陣和信號的維數過大,導致了存儲和計算負擔急劇增加,影響了KCS算法進一步應用。為了降低測量矩陣和信號維數,文獻[10]首先將三維數據切片,再沿著一維疊加,將三維張量轉換為二維矩陣。然后利用降維二維平滑l0范數(Dimension Reduction2D Smoothedl0-norm,DR-2D-SL0)重構方法求解稀疏優化問題,得到散射體的二維圖像。最后,通過將得到的二維圖像重新還原成三維張量來得到三維圖像。文獻[11,12]首先將信號表示為張量和矩陣的模態積形式,然后采用一種稀疏多維度平滑l0算法(MultiDimensional Smoothedl0-norm,MD-SL0)恢復三維圖像,由于該算法能夠直接處理三維圖像,所以具有較低的計算復雜度和內存消耗,能夠有效地進行三維重建。但是該方法需要調整的參數較多,并且在低信噪比條件下圖像恢復效果一般。文獻[13]將ADMM算法融入稀疏孔徑成像ISAR自聚焦中,利用部分傅里葉矩陣字典將矩陣求逆轉化為元素除法,并將二維ISAR圖像的距離單元更新變為整體更新,在數秒內就能獲得聚焦良好的圖像。
受文獻[13]的啟發,本文基于ADMM算法提出了一種MIMO-ISAR成像方法。首先建立多維回波欠采樣模型,然后利用ADMM算法解決欠采樣數據的稀疏約束欠定問題。為了提高計算效率、降低存儲消耗,該方法將高維的測量矩陣分解為張量的模態積,用張量元素除法替代計算效率低的矩陣求逆。仿真和實測數據都驗證了所提方法的有效性。下面給出本文的符號定義,?表示兩個矩陣的克羅內克積;×n(n=1,2,3)表示張量和矩陣的n模態積;張量用大寫花體字母表示,如A。
2 信號模型
圖1為成像場景圖,其中X軸沿著收發陣列方向,選取一發射節點為坐標原點O,Y軸和Z軸分別按照右手定則確定。飛機以速度為v0作勻速直線運動,且速度方向與陣列方向相垂直。
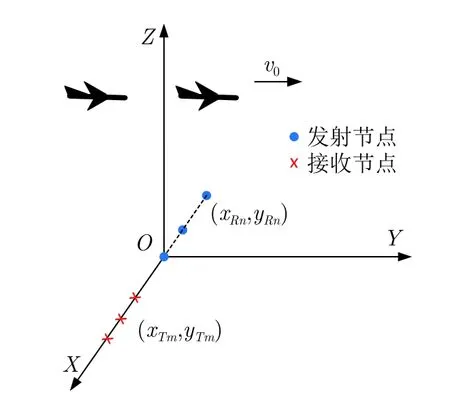
圖1 成像場景圖Fig.1 Geometry of imaging
圖1的線性收發陣元如圖2所示,假設有M1個發射陣元和N1個接收陣元,其中發射陣元的間距為2N1d,接收陣元的間距為 2d。根據文獻[14],上述收發陣列可以等效成A=M1N1個等效收發陣元,且等效收發陣元成線性均勻排列,陣元間距為d。
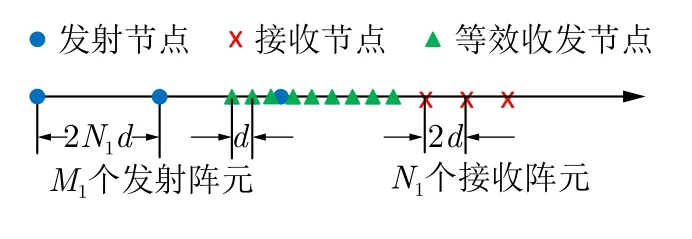
圖2 線性收發陣元的等效收發陣元示意圖Fig.2 The equivalent transceiver array element for linear receiving and transmitting array elements
假設發射陣列發射步進頻信號,發射頻率fb=fc+(b ?1)Δf,其中fc為發射信號中心頻率,Δf為頻率步長。經過信號分選后,第a個等效收發陣元在第p個快拍時刻的接收信號可以表示為
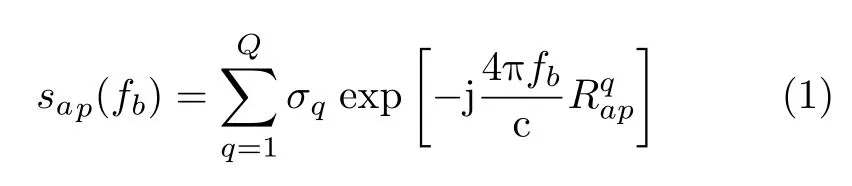
其中,a=1,2,···,A表示等效收發陣元序號,A為等效陣元總數;q=1,2,···,Q表示散射點序號,Q為散射點總數;p=1,2,···,P表示快拍序號,P為快拍數;c為光速;σq為第q個散射點的散射強度;表示第a個等效收發陣元在第p個脈沖時刻到第q個散射點的距離。
如圖3所示,目標在ZOY面沿著Y軸方向以速度v0作勻速直線運動,假設初始快拍時刻,目標參考點位于O0,第p個快拍時刻參考點位于Op,φa ≈(a ?1)d/R0+α0為第a個等效陣元與Z軸夾角,θp ≈ω(p ?1)Tp為OOp與Z軸夾角。其中d為等效陣元間的距離,ω為目標運動等效轉速,Tp為脈沖重復時間,R0為等效收發陣元中心到目標的距離,ω ≈v/R0,α0為第1個等效收發陣元與Z軸夾角。則在第p個快拍時刻,坐標系中q點坐標轉變為坐標系中的坐標其中軸由O和O0的連線確定,軸和軸分別由右手定則確定;軸由第a個等效陣元和Op的連線確定,分別由右手定則確定。則經過平動補償后,式(1)中的回波信號可以表示為
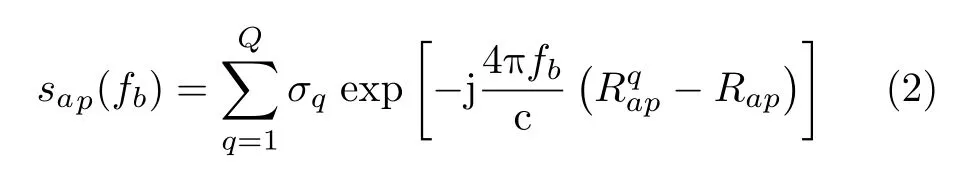
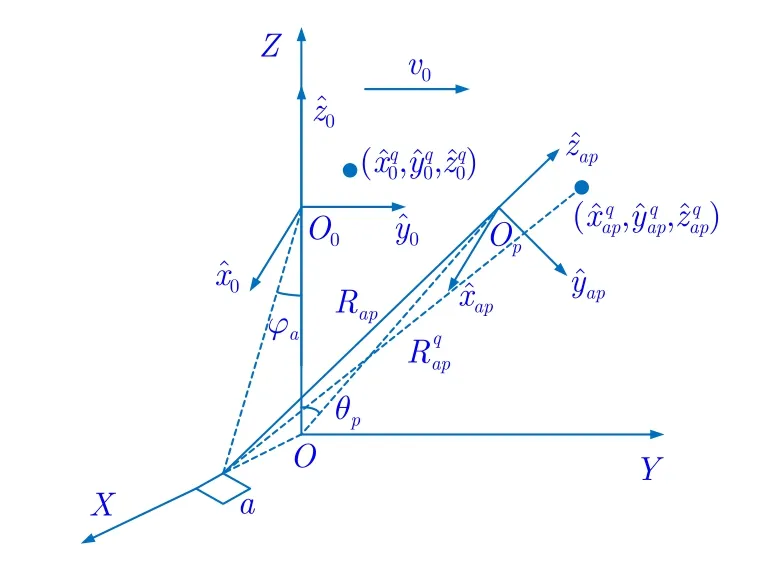
圖3 目標移動示意圖Fig.3 Motion of the target
其中,Rap表示第a個等效陣元到轉動中心Op的距離。則

將式(4)代入式(2)可得
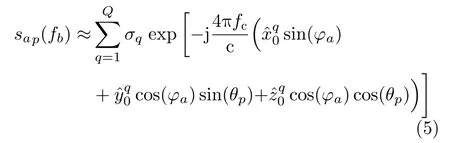
當發射信號帶寬遠小于中心頻率fc時,可近似認為fb/c≈fc/c,假設α0≈0,在遠場條件下且觀測時間較短時,則d ?R0,φa ≈0,θp ≈0。則式(5)可以近似為
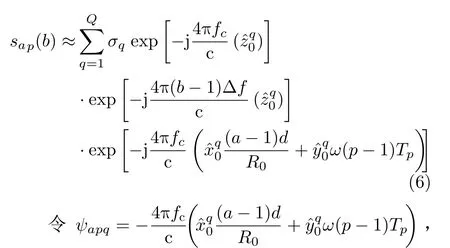
則通過對x方向的相位求偏導數,可以得到沿x方向相位變化為
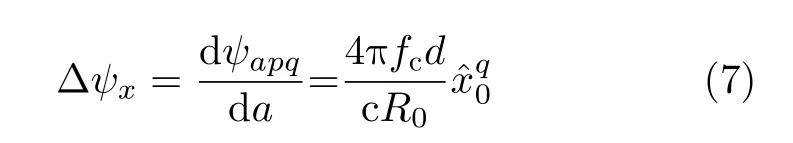
假設兩個散射中心在x方向上的距離為 Δx,則總相位差可表示為
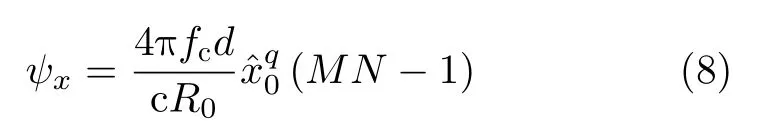
當滿足ψx ≥2π時,兩個散射點在x方向才能被分辨,所以x方向上的分辨率為
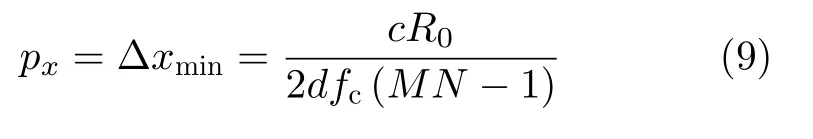
同理可得y方向的分辨率為
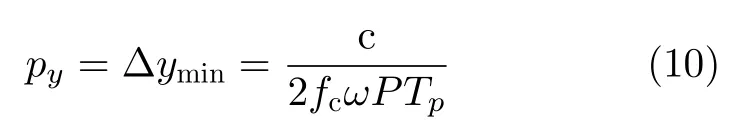
而z方向的分辨率為pz=c/(2Bw),其中Bw為信號帶寬。所以對a,b,p3個維度分別做傅里葉變換就能得到三維圖像。所以信號的張量模型可以表示為
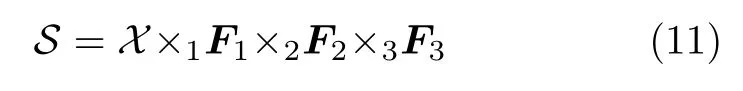
其中,×n(n=1,2,3),表示張量和矩陣的n模態積,S ∈CA×P×B表示三維信號,X ∈CA×P×B表示三維圖像。F1∈CA×A,F2∈CP×P,F3∈CB×B表示全傅里葉變換矩陣。
當陣元數目減少,或由于噪聲或硬件原因導致完整回波出現缺失時(相當于對回波的3個維度做稀疏采樣),如果繼續采用傅里葉變換將會導致圖像質量嚴重下降。因此我們利用圖像的稀疏性,引入壓縮感知方法對回波信號進行處理,用較少的數據就能恢復圖像。但是傳統的壓縮感知算法需要將三維數據展開成一維形式。將式(11)展開成一維形式為
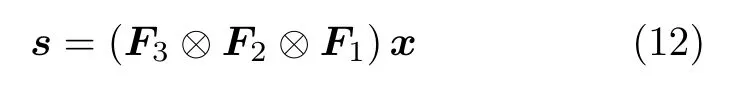
其中,符號?表示克羅內克積,s=vec(S),x=vec(X)。假設三維信號的維度為60×60×60,當轉化為一維信號后,感知矩陣的維度為21600×21600,這需要消耗巨大的內存和存儲容量,限制了算法的進一步使用。所以針對上述問題,本文采用多維ADMM(MultiDimensional ADMM,MD-ADMM)算法對圖像進行稀疏重構。
3 多維ADMM稀疏成像方法
3.1 多維ADMM算法
下面以ADMM算法為基礎,推導MD-ADMM算法,首先推導算法的三維張量形式,再推廣到多維情形。當完整回波出現缺失時,式(11)可以表示為
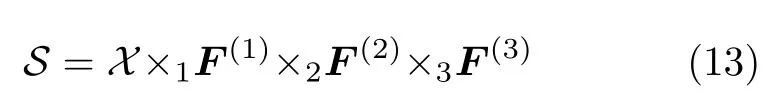
其中,S ∈CM×N×K表示降采樣信號,X ∈CU×V×W為待恢復圖像。設完整信號維數為U ×V ×W,M,N,K分別為對信號3個維度的采樣數。F(1)∈CM×U,F(2)∈CN×V,F(3)∈CK×W,分別為3個維度的部分傅里葉變換矩陣。令F(1)=T1F1,F(2)=T2F2,F(3)=T3F3,其中F1,F2,F3分別為維數為U ×U,V ×V,W ×W的全傅里葉矩陣。T1∈CM×U,T2∈CN×V,T3∈CK×W為傅里葉采樣矩陣。令G,H,J分別表示對張量S3個維度的采樣序列,其中,G ∈[1,2,···,U]T,H ∈[1,2,···,V]T,J ∈[1,2,···,W]T其序列長度分別為M,N,K。則
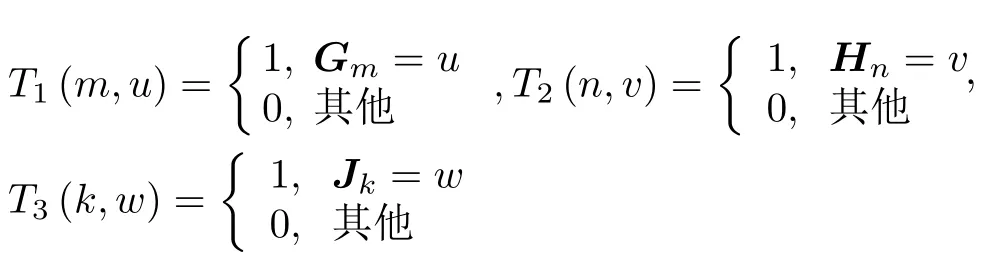
將式(13)展開成一維形式為
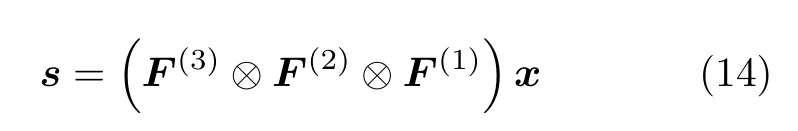
其中,s=vec(S),x=vec(X),其中vec(·)表示將張量向量化。在式(14)的信號模型中,直接從已知信號s中重構出x將有無窮多組解,屬于病態問題,因此需要引入額外條件,壓縮感知理論可以利用待恢復信號的稀疏性從無窮多組解中找出最稀疏的解。雷達圖像通常由若干強散射點組成,因此待恢復信號x的稀疏性一般情況下是成立的。理想情況下通常用l0范數表示信號的稀疏性,但是基于l0范數最小化的稀疏恢復問題不易求解,屬于NP難問題。因此,一般采用l1范數替代l0范數,并且l1范數最小化問題通常可以轉化為凸問題。本文采用ADMM算法[15]解決基于l1范數的最小化問題,該方法可以將高維的測量矩陣分解為張量的模態積,用張量元素除法替代了計算效率低的矩陣求逆,提高了計算效率。因此式(14)中,基于l1范數最小化優化問題可以表示為
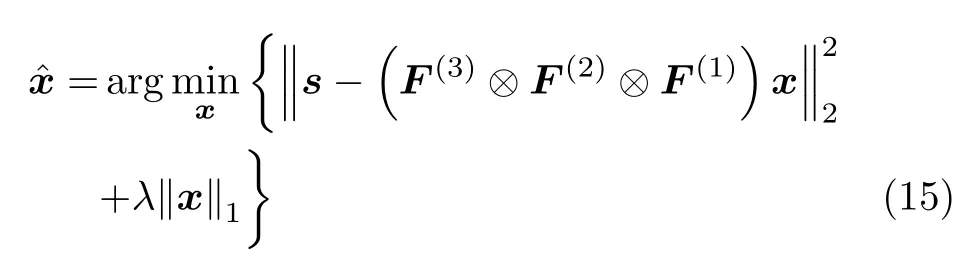
引入輔助變量z,則原基于l1范數的最小化問題可以等價于以下帶等式約束的優化問題
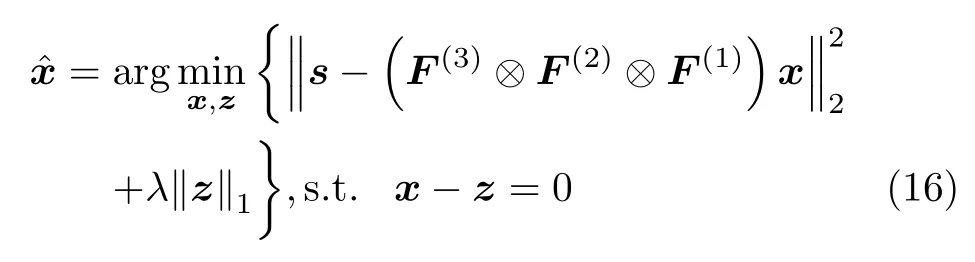
其增廣拉格朗日函數可以寫為
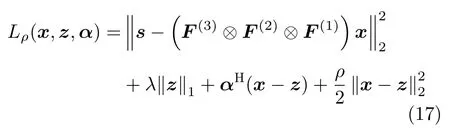
其中,α為對偶變量,ρ為懲罰系數,ADMM算法將式(15)中的問題分解為如式(18)的3個子問題
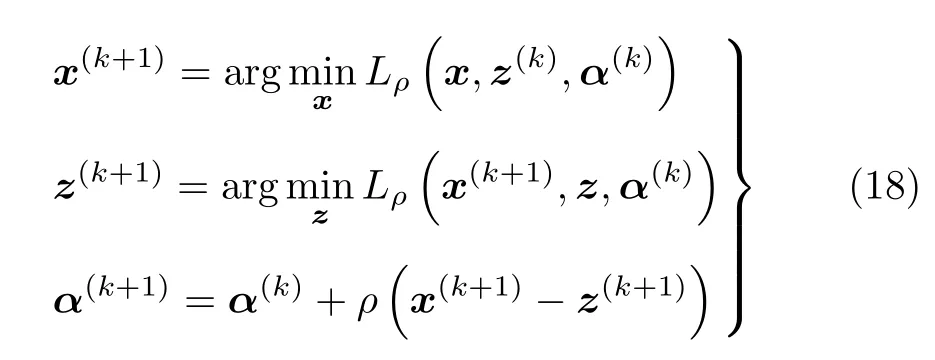
其中,上標k表示第k次迭代,式(18)中前兩個子問題可以通過對函數Lρ(x,z,α)中的x和z分別求導并令導數為0求得,經求解式(18)中x,z以及α的迭代式為
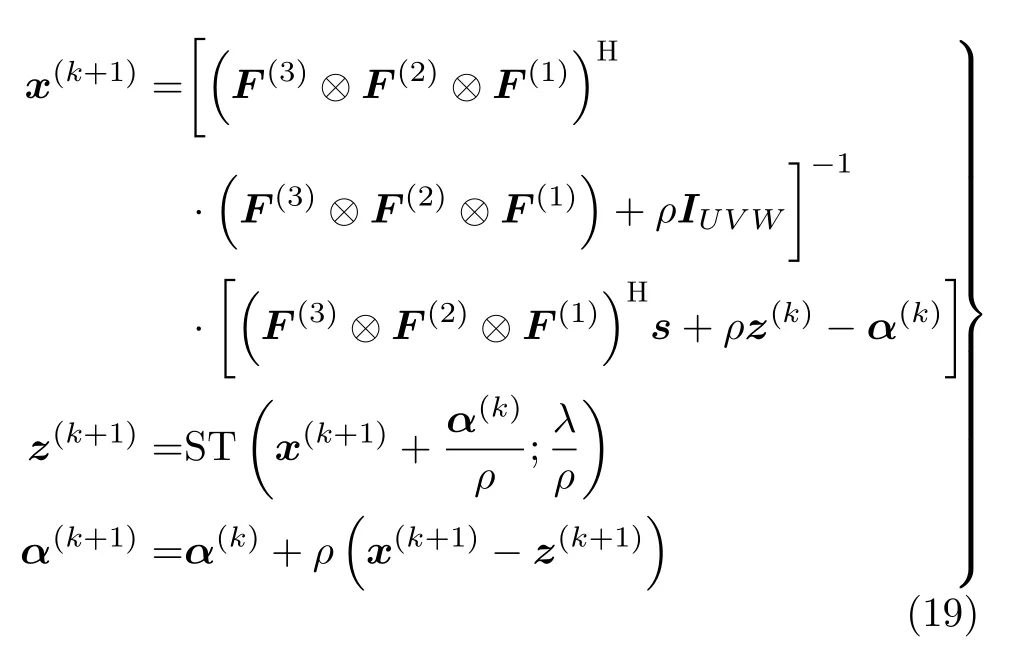
其中,ST為軟閾值(Soft Threshold)函數,其表達式為ST(x,a)=(x/|x|)max(|x|?x,0)。將F(1)=T1·F1,F(2)=T2F2,F(3)=T3F3代入式(19)可得
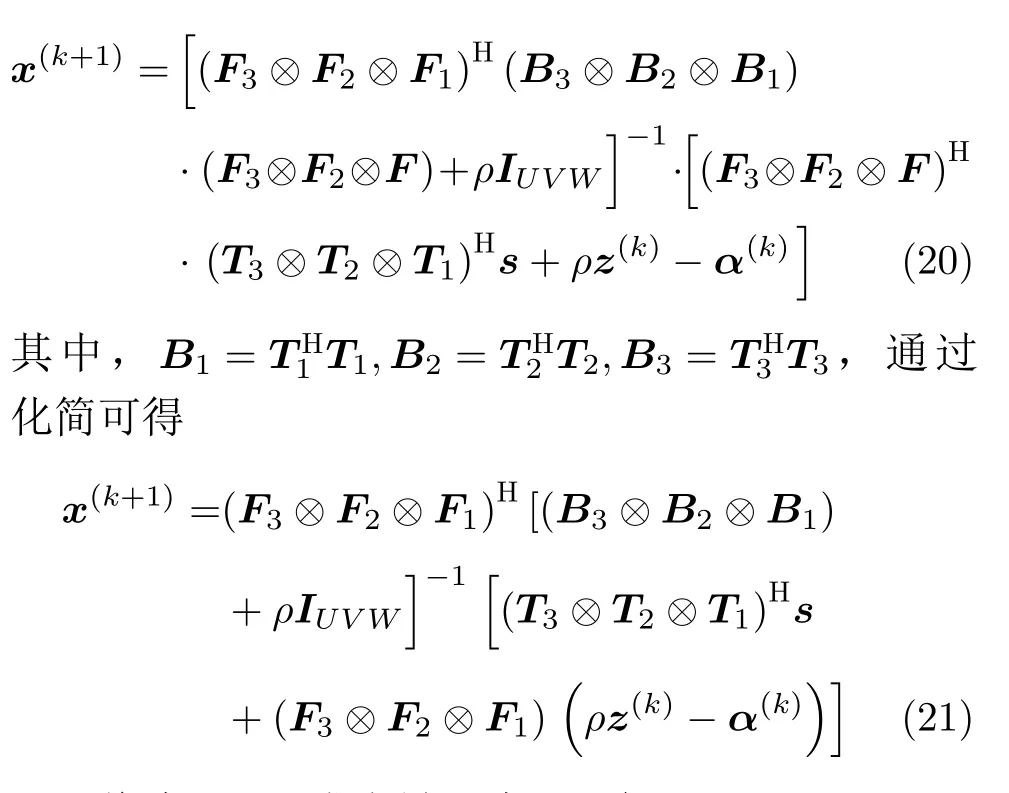
將式(21)寫成張量形式,可得
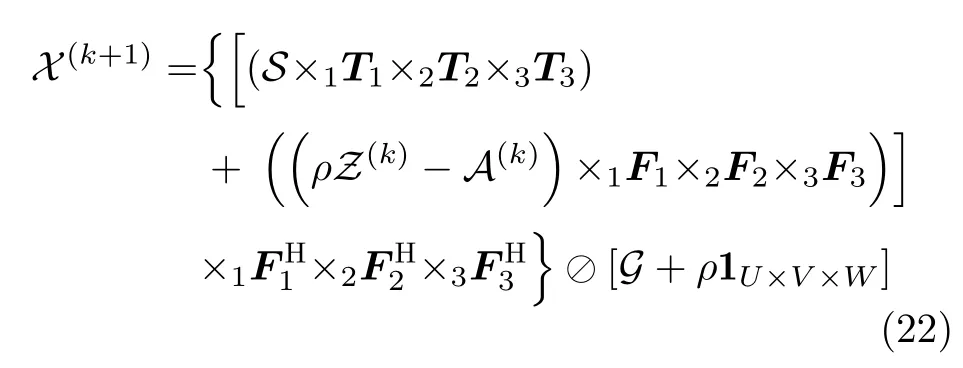
其中,1U×V×W表示元素全為1、維數為U ×V ×W的三維張量,?表示張量的元素除法,G表示對接收回波三維方向的采樣,其值設為0或1,分別表示是否被采樣到。同理式(19)中z(k+1)和α(k+1)的迭代式同樣可以寫成如式(23)和式(24)的張量形式
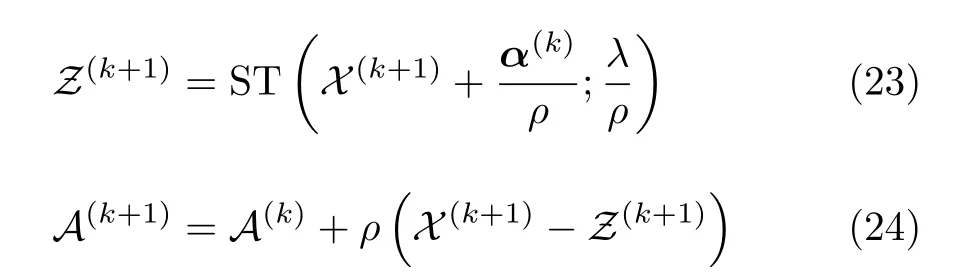
聯合迭代式(22)—式(24),就可得到圖像X。初始參數設置如下:Z和A的初值設定為0,λ的值根據數據進行調整,ρ的值取1。
將三維形式進一步推廣,假設多維張量的維數為U1×U2×···×Ui,則張量X(k+1)的更新表達式為
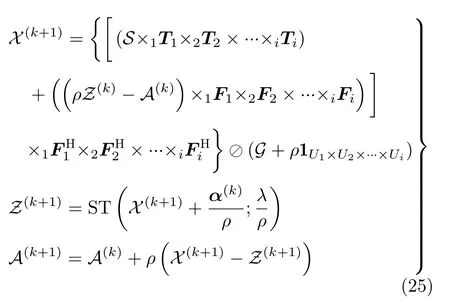
3.2 計算復雜度分析
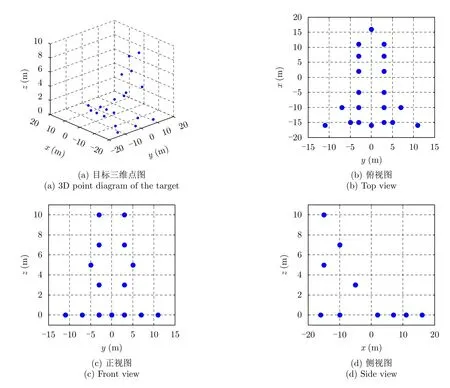
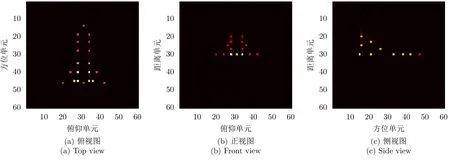
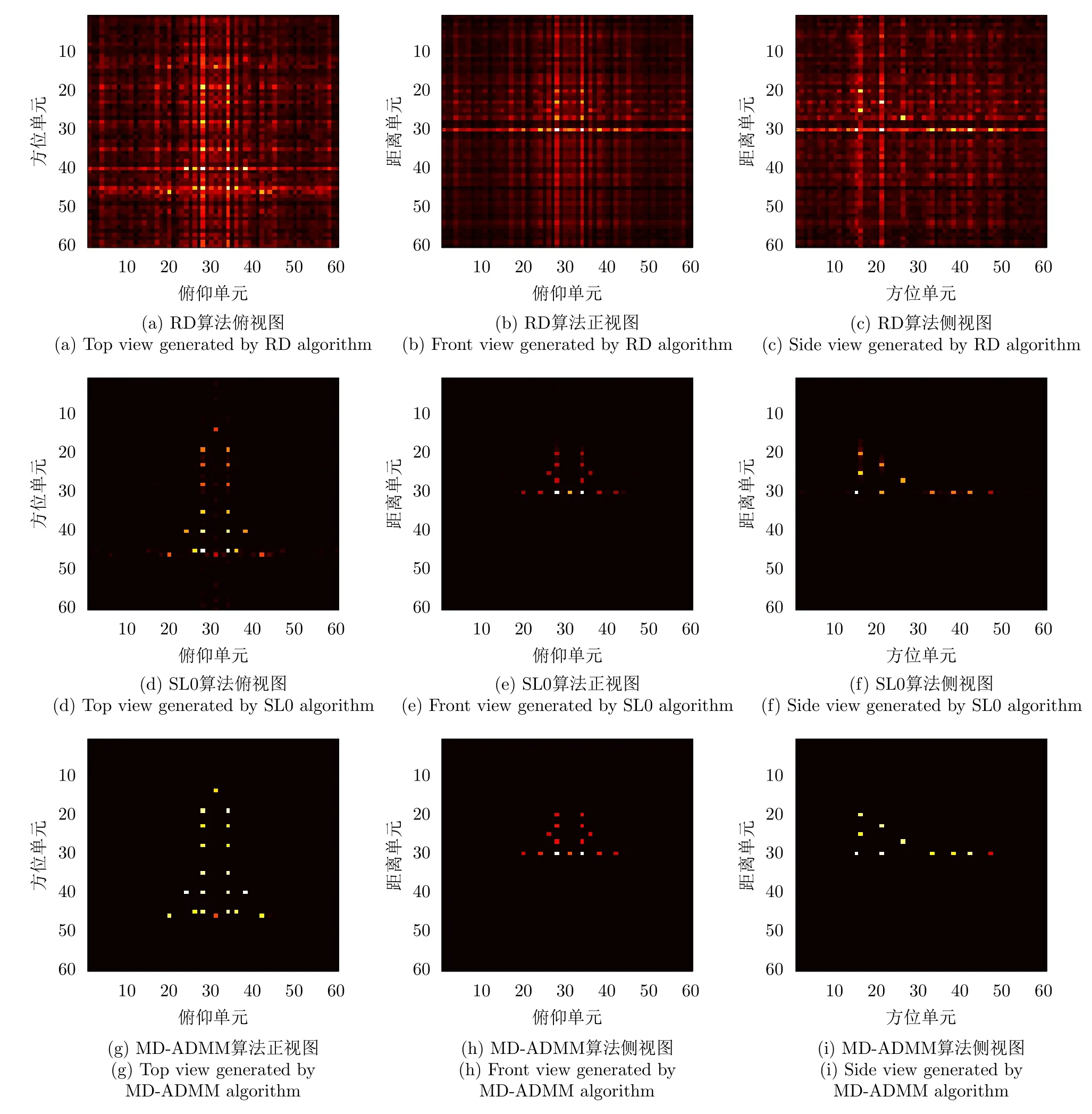
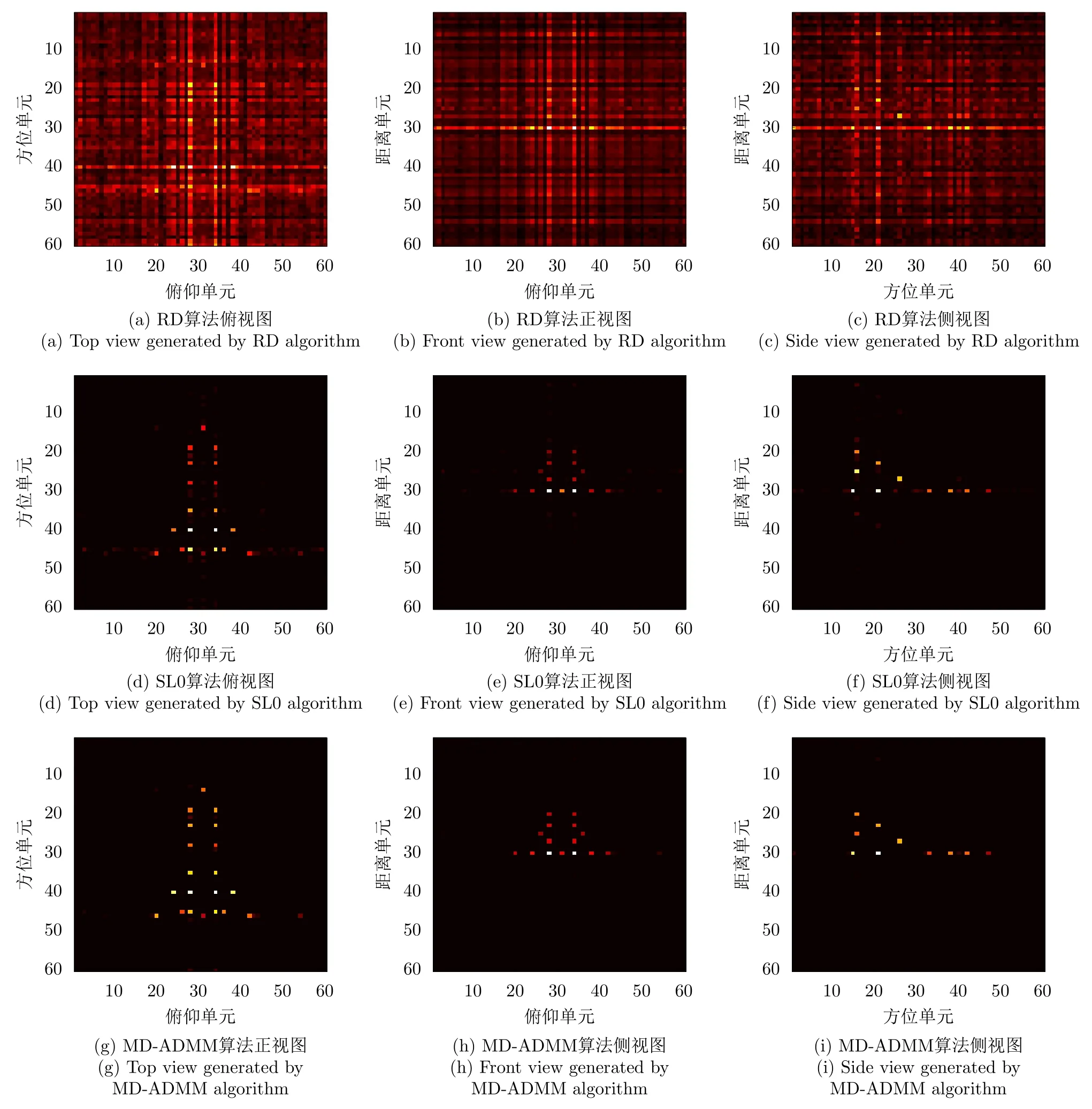
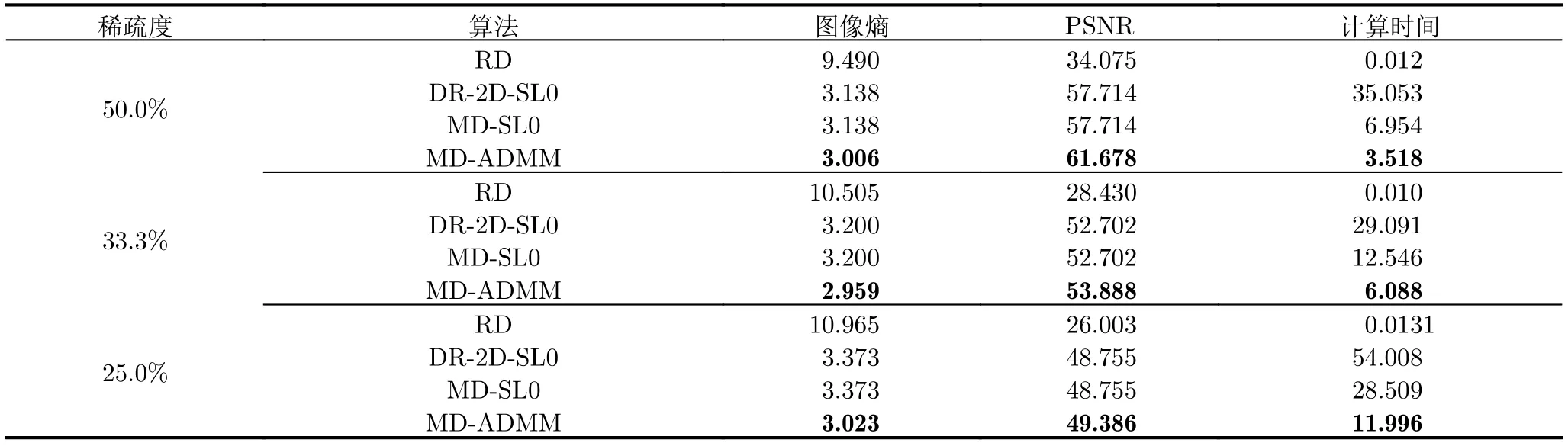
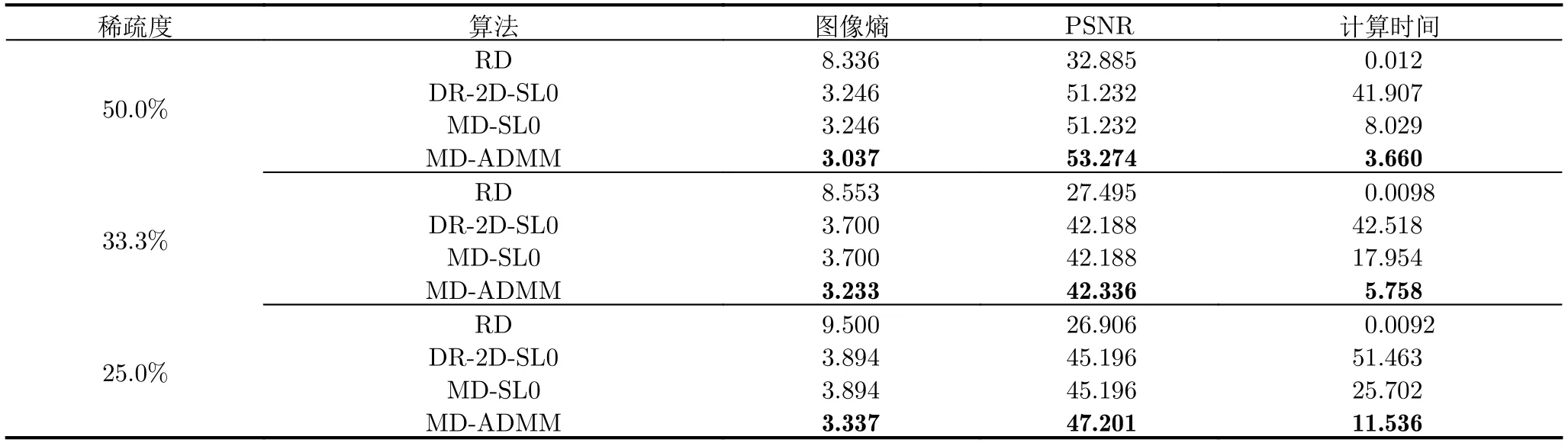
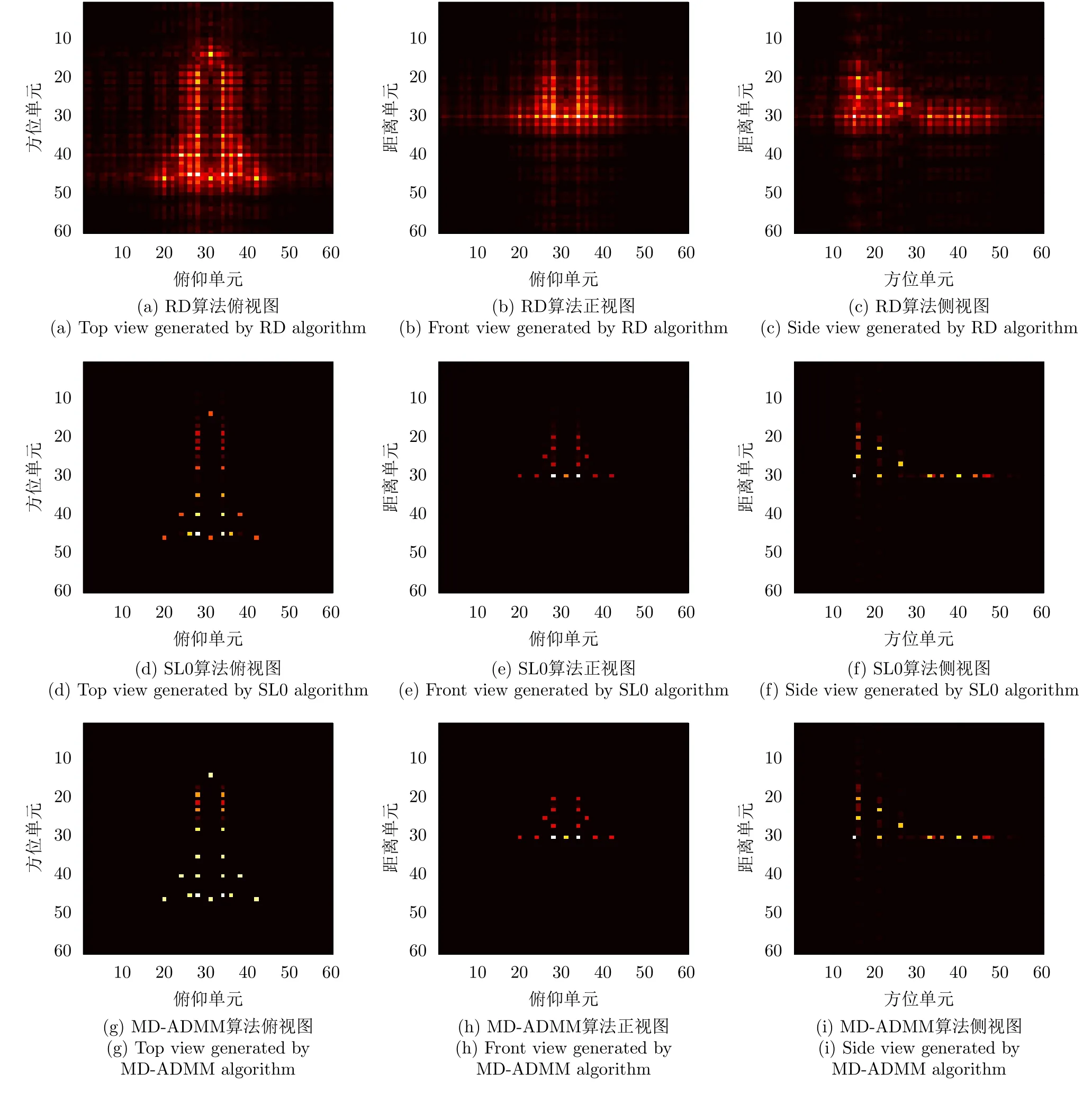
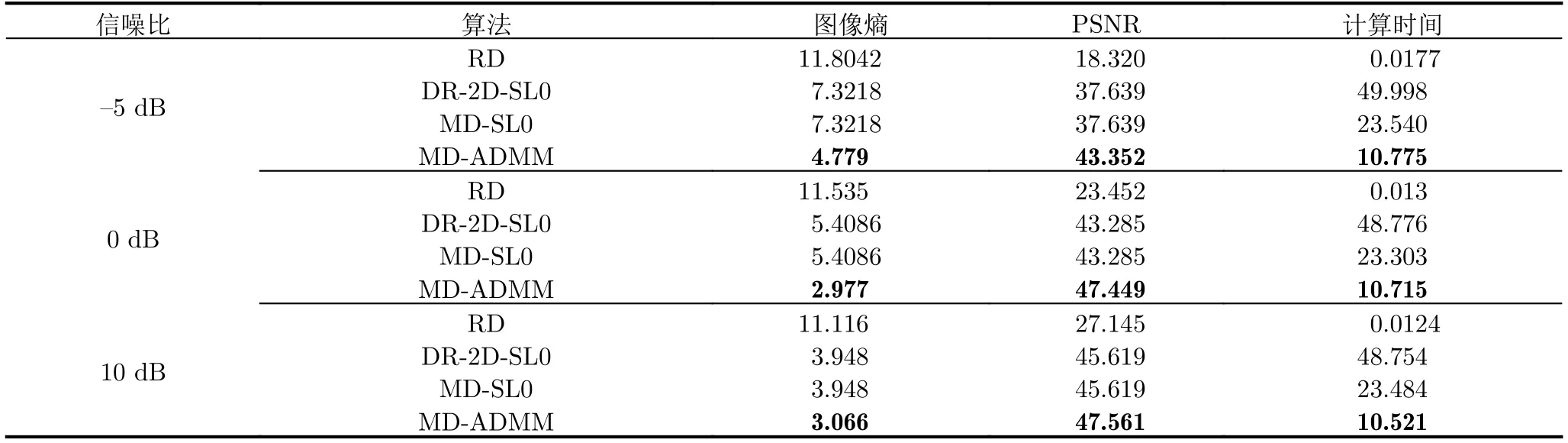
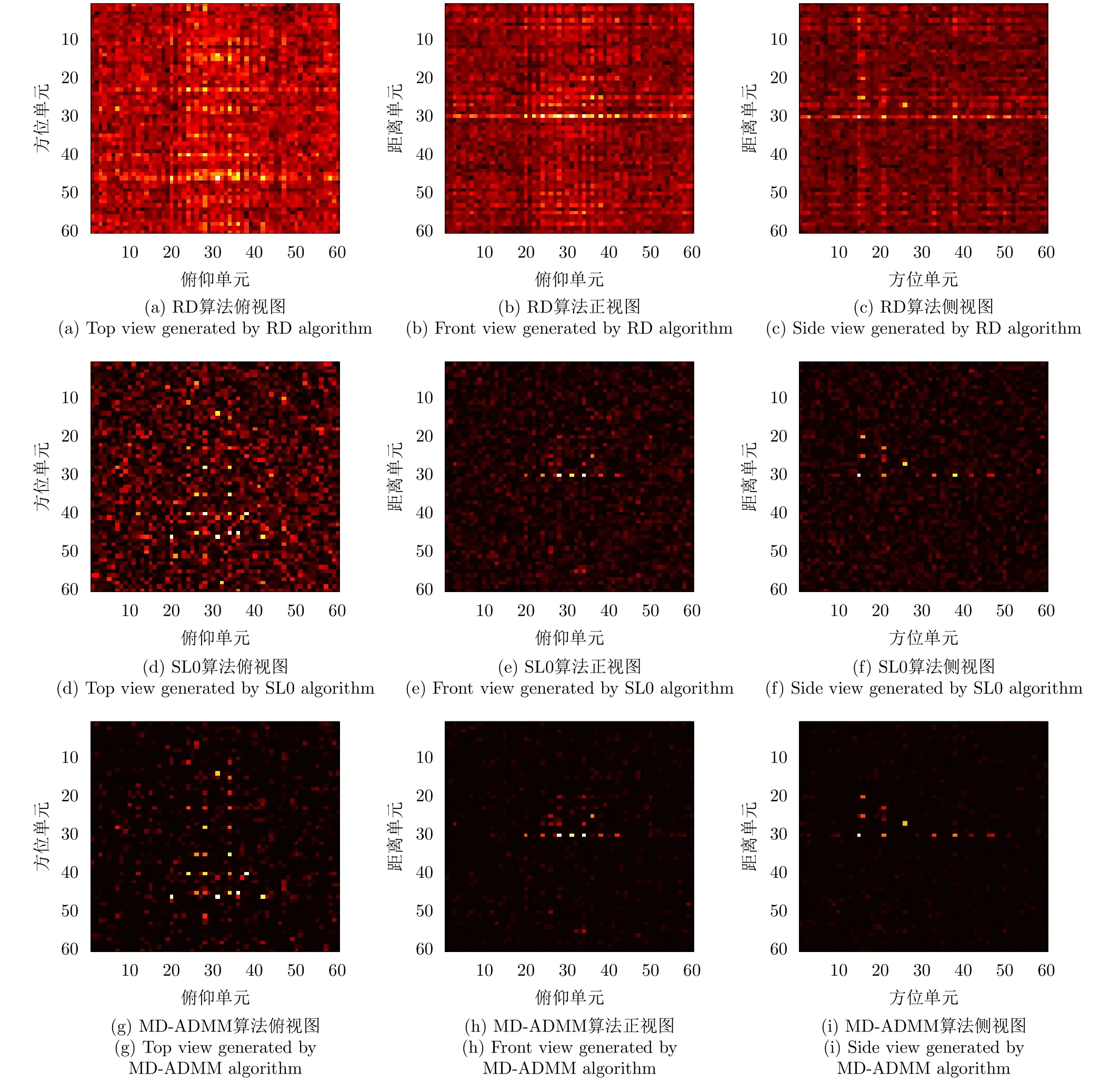
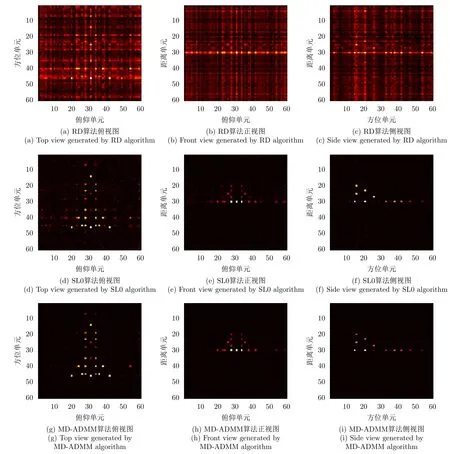
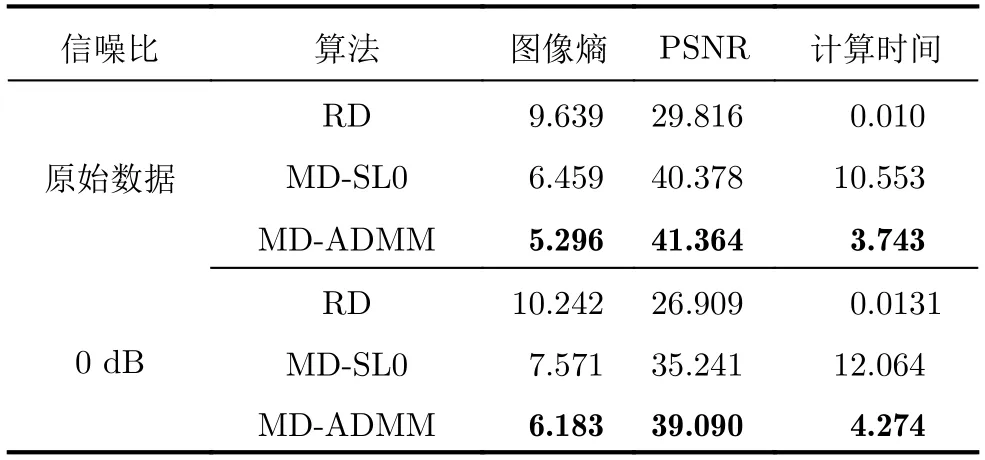
MD-ADMM算法中圖像X更新表達式(22)的計算復雜度為:O{[MNKU+UVNK+UVKW+2(U2VW+V2UW+W2UV)]假設經過L1次迭代后算法停止,則總的算法復雜度可以表示為:O{[MNKU+UVNK+UVKW+2(U2VW+V2UW+W2UV)]L1}。根據文獻[10],算法DR-2D-SL0的計算復雜度為O{(UVMNK+MNUVW+MNWK+UVKW)L2L3},其中L2和L3分別為第1層循環和第2層循環的迭代次數。根據文獻[5],算法MD-SL0的計算復雜度為O[(MNKU+UVNK+UVKW+UVWM+MNVW+MNKW)L2L3]。在本實驗中,迭代次數L2L3?L1,且算法DR-2D-SL0的單次迭代計算復雜度最高,因此3種算法的計算復雜度排序為:MD-ADMM 實驗仿真數據設置如下:目標飛行速度v0=200m/s,雷達距目標中心的距離R0=10000m,發射信號中心頻率fc=10GHz,帶寬Bw=150MHz,發射步進頻信號個數B=60。設收發陣列為10發6收MIMO線陣,等效收發陣元個數A=60,等效收發陣元間距d=2.5m。脈沖重復頻率PRF=80Hz,快拍數P=60。仿真中使用的點散射模型如圖4所示。 圖4 仿真目標三維散點圖Fig.43 D scatter of simulation target 當回波數據完整時,對3個維度直接進行傅里葉變換后得到的圖像如圖5所示。由圖5可知當回波數據完整時,直接對3個維度做傅里葉變換可以得到質量較高的三維圖像。本文提取圖5中的三維散點坐標,將散射點所在位置幅值設為1,圖像中其余位置幅值設為0,形成參考三維圖像H。下面對稀疏采樣回波進行成像,為了獲得三維稀疏回波,對回波進行稀疏采樣,具體采樣方式如圖6所示。 圖5 完整回波數據圖像三視圖Fig.5 Three views of image with the complete echo 圖6 回波采樣形式Fig.6 Undersampling masks of random sampling and block sampling 首先采用隨機采樣方式,對稀疏度(每個維度的稀疏度相同)分別為50.0%,33.3%,25.0%的回波進行三維成像處理,其中信號添加信噪比為20dB的高斯白噪聲。分別采用RD,MD-SL0,DR-2D-SL0,MD-ADMM4種算法對目標進行三維成像(其中算法MD-SL0和算法DR-2D-SL0統稱為SL0算法),并采用三視圖進行展示。在實驗中本文調整參數讓每一種算法都達到其最佳成像效果。圖7—圖9分別為稀疏度為50.0%,33.3%,25.0%的不同算法成像結果。由圖7—圖9可知,當回波稀疏時,由于受到旁瓣干擾,傳統RD算法將會失效,得到的圖像分辨率較低。由于利用了圖像的稀疏性,采用了壓縮感知方法,算法DR-2D-SL0,MD-SL0,MD-ADMM都得到了質量較高的圖像。 圖7 稀疏度為50.0%時圖像Fig.7 Image when sparsity is50.0% 圖8 稀疏度為33.3%時的圖像Fig.8 Image when sparsity is33.3% 圖9 稀疏度為25.0%時的圖像Fig.9 Image when sparsity is25.0% 為了進一步定量比較4種算法,表1給出了隨機稀疏采樣條件下4種算法數值結果,其中包括圖像熵、峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)以及計算時間。在圖像處理領域,圖像熵和PSNR可以一定程度上反映圖像質量。在三維圖像中圖像熵的定義為式(26) 其中,Sum(·)表示張量的所有元素之和,C=U,V,W分別為張量X的維數。假設對X進行了歸一化,則X相對于參考圖像H的均方誤差可以表示為 其中,huvw為參考三維圖像H的元素。定義PSNR為 由表1以及圖7—圖9可知,雖然RD算法計算效率最高,但是圖像質量最差。由于參數設置一致,算法DR-2D-SL0和MD-SL0圖像熵與PSNR相同,但是MD-SL0算法直接對三維張量進行處理,而DR-2D-SL0要將三維張量展開成二維矩陣,這增加了計算量,所以MD-SL0的計算時間更短,計算效率更高。與其余基于壓縮感知算法相比,所提MDADMM算法在不同稀疏度下的圖像熵最小,峰值信噪比最大,并且計算時間最短,這驗證了所提算法的有效性。 表1 隨機稀疏采樣條件下數值結果Tab.1 Numerical results under random sparse sampling condition 接著采用塊稀疏采樣方式,對稀疏度(每個維度的稀疏度相同)為50.0%,33.3%,25.0%的回波進行成像處理。圖10為采用不同算法對信噪比為20dB,稀疏度為50.0%的回波進行處理后得到的圖像。表2為塊稀疏采樣條件下不同算法的數值結果,由圖10和表2可知,所提MD-ADMM算法在不同稀疏度的塊稀疏采樣條件下得到的圖像熵最小,峰值信噪比最大,并且計算時間最短,這驗證了所提算法的有效性。 表2 塊稀疏采樣條件下數值結果Tab.2 Numerical results under block sparse sampling condition 圖10 稀疏度為50.0%的塊稀疏采樣圖像Fig.10 The image of a sparsity of50.0%by block sampling 下面比較不同算法在相同稀疏度(3個維度的稀疏度相同),不同信噪比下的成像性能,其中回波信號采用隨機采樣方式,每個維度的稀疏度均為25.0%,并添加均值為0的高斯白噪聲。圖11—圖13分別為在信噪比為–5,0,10dB條件下不同算法得到的目標三視圖。表3為不同信噪比條件下的數值結果。由圖11—圖13和表3可知,在稀疏孔徑條件下RD算法基本失效。在不同信噪比條件下,所提MD-ADMM算法圖像熵最小,PSNR最大,并且計算時間最短,這證明了所提算法對噪聲的魯棒性最強。 表3 不同信噪比條件下數值結果Tab.3 Numerical results under different SNR conditions 圖11 稀疏度為25.0%信噪比為–5dB的圖像Fig.11 The image when sparsity is25.0%and SNR=–5dB 圖12 稀疏度為25.0%信噪比為0dB圖像Fig.12 The image when sparsity is25.0%and SNR=0dB 圖13 稀疏度為25.0%信噪比為10dB的圖像Fig.13 The image when sparsity is25.0%and SNR=10dB MIMO雷達實驗系統目前還在搭建中,還存在發射信號帶寬過窄、收發陣列同步性差等問題,導致MIMO-ISAR回波目前還難以獲取,也是下一步要著重解決的問題。因此采用二維Yak-42飛機ISAR實測數據,以驗證所提MD-ADMM算法在有限采樣數據條件下的有效性。實驗數據參數設置如下:雷達發射信號的載頻為5520MHz,信號帶寬為400MHz,快時間采樣頻率為10MHz,脈沖寬度為25.6μs,觀測目標為Yak-42飛機。假設接收信號已經做了包絡對齊、平動補償以及自聚焦,共接收到256個脈沖,每個脈沖信號包含256個快時間采樣。本文采樣稀疏采樣方式,抽取96個脈沖,以及128個快時間信號。圖14為不同算法對二維稀疏信號成像結果。圖15為圖14信號中添加0dB的高斯白噪聲的結果。表4為不同算法在不同信噪比條件下的數值結果。由圖14、圖15以及表4可知,RD算法基本失效,算法MD-SL0,MD-ADMM在二維稀疏采樣條件下依然能夠得到清晰圖像,但相比MDSL0算法,MD-ADMM算法得到的圖像熵最小,峰值信噪比最大,并且計算時間最短,進一步驗證了所提算法的有效性。 圖14 實測數據結果Fig.14 Measured ISAR data results 圖15 信噪比為0dB實測數據結果Fig.15 Measured ISAR data results under SNR=0dB 表4 實測數據不同信噪比條件下的數值結果Tab.4 Numerical results of measured data for different signal-to-noise ratio conditions 本文提出一種多維ADMM稀疏恢復算法,本算法可以用于恢復多維稀疏信號,而無需將多維信號轉換為一維,這極大地減少了存儲量和計算量。通過該算法,實現了一種實用的MIMO-ISAR成像。與其他算法相比,本算法具有存儲容量小、計算效率高、成像質量好的優點。仿真和實測數據結果均證明了本算法的有效性。4 實驗仿真
4.1 仿真數據分析


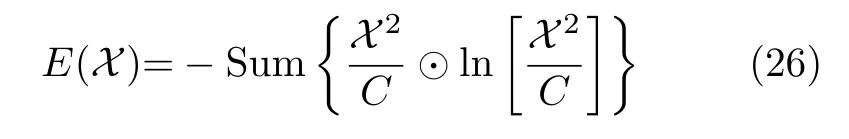
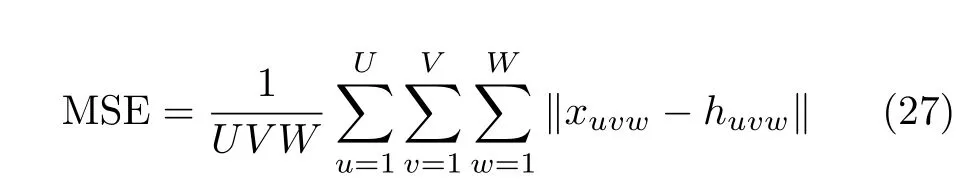
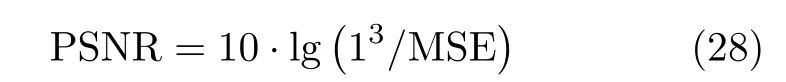

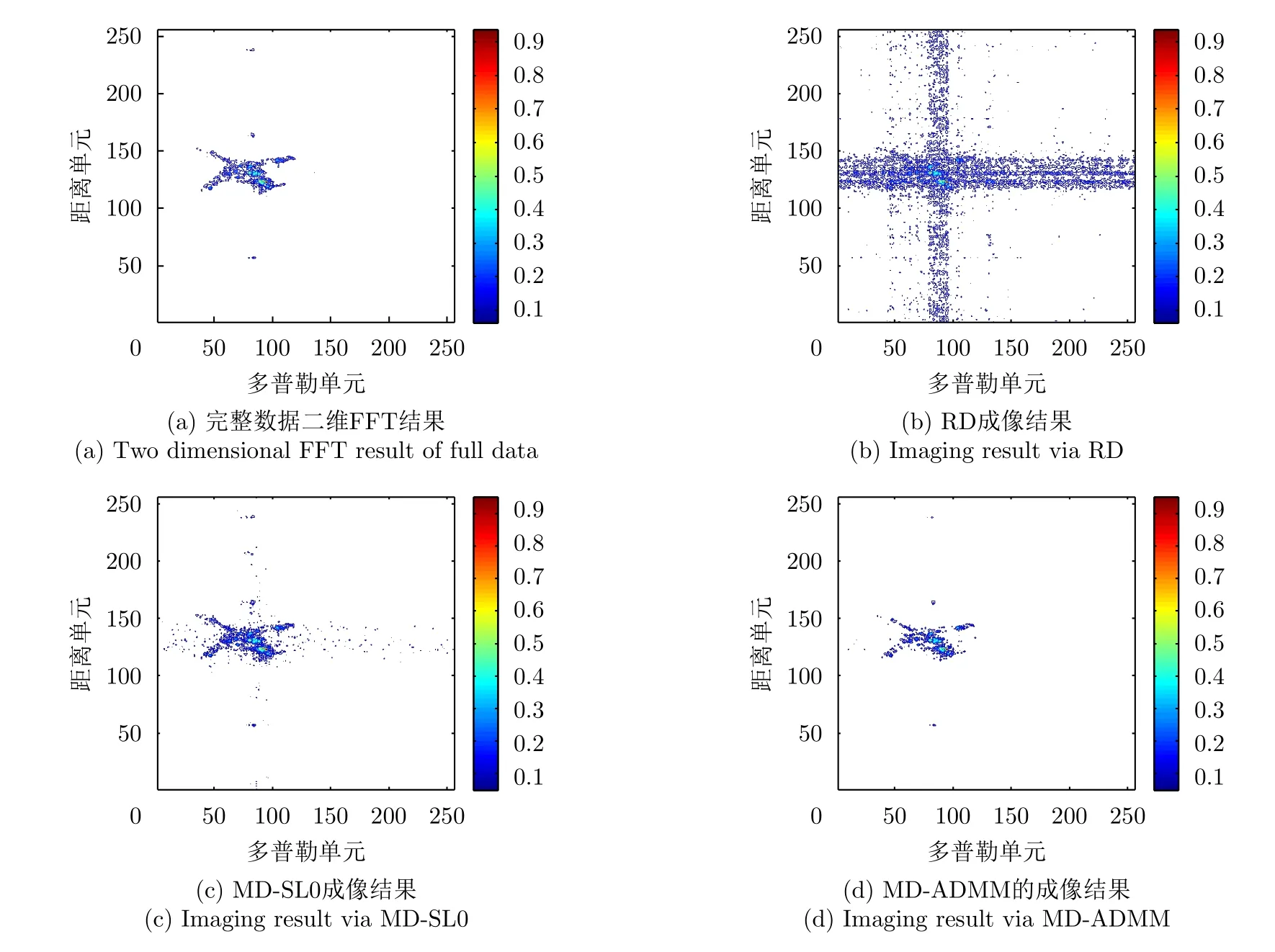
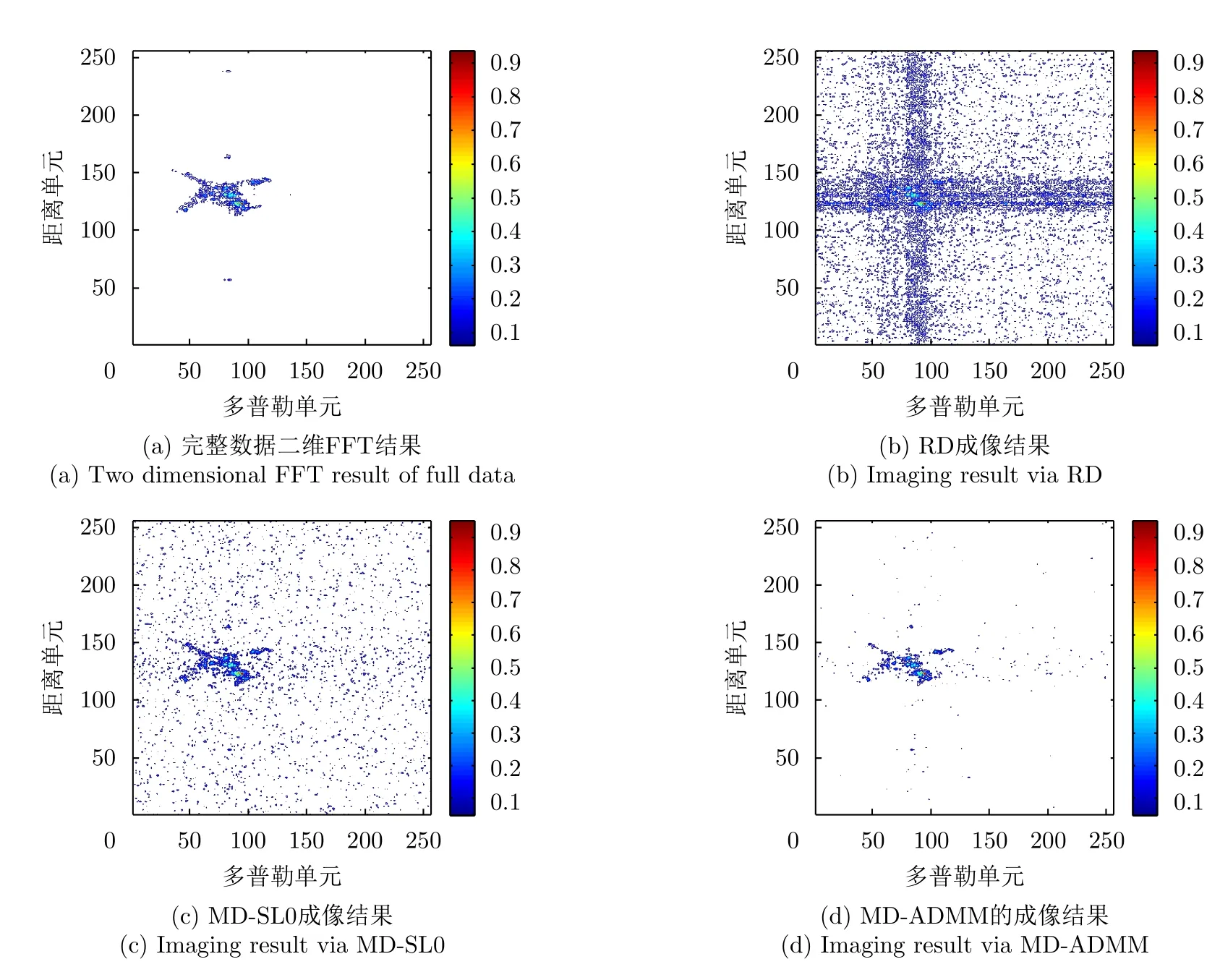
4.2 實測數據分析
5 結論

