基于校車數量的無混載校車路線問題模型優化實現
高 巍,陳澤穎,李大舟
(沈陽化工大學 計算機科學與技術學院, 遼寧 沈陽 110142)
隨著中國義務教育水平的不斷提高,為中小學生提供合理的校車服務成為對學校和教育部門的新要求.對地方教育局而言,正確規劃校車路線并盡可能降低校車運營成本是一個難題[1].校車路徑問題主要是為一個校車車隊規劃路線,使校車沿路線將學生送至學校或放學時送回乘車站點,并使特定的目標達到最優.校車不僅可以很大程度上提高道路利用率,而且還能節省大量的能源.相對于其他的出行行為,上下學出行行為在時間上和空間上都具有一定的確定性,這在一定程度上不僅影響人們的日常活動,而且還對城市交通有著不可忽視的影響[2].
文獻[3-6]表明通過校車路徑優化能夠顯著減少校車數量或校車行駛距離,從而降低校車運營成本.文獻[3]分析紐約市路徑問題的各個方面,包括在曼哈頓區建立路線,并提供一種解決方案,方案的校車數量遠遠少于目前使用的校車數量.文獻[4]開發了一個解決方案程序,分別考慮每個目標并搜索一組有效的解決方案,而不是單一的最優解決方案.文獻[5]以車輛數為優化目標,設計了一個“后啟發”算法進行求解,求解過程中對不同車型的校車進行分配,并不考慮不同車型的固定成本和可變成本的差異.孟凡超等[6]利用禁忌搜索進行求解,主要采用插入法和交換法獲取鄰域解.以上算法僅考慮了車輛容量約束,優化目標是最小化車輛行駛距離,主要利用已有求解VRP(vehicle routing problem)的算法框架,通過引入需求拆分算子進行求解.
本文側重于校車的最少運營數問題,對校車問題進行定義和描述,將問題分為極限情況和一般情況,針對不同情況設計了SBLS(school bus limit situation)算法和SBGS(school bus general situation)算法,并在沈陽市某校進行實驗驗證,達到了運營成本降低的預期效果.
1 上下學時校車的最少運營數量問題
1.1 問題定義
校車無混載指的是一輛校車只為一所學校服務,一輛校車只負責一個學校學生的上下學接送[7].將一所學校全部乘校車的學生作為一個優化的目標,對校車乘降站、校車行駛路徑、校車數量和每輛校車負責接送哪些學生進行優化.由于高額的運營費用以及不同于公交客運的運營模式,因此減少校車的數量即從源頭上降低了校車的運營成本.若只考慮成本而無限減少校車數量將會造成行程路徑的增加和時間的延長,導致學生可能上學遲到、家長滿意度下降等問題.解決該問題就是在確保學生正常上下學的基礎上,將運營成本降到最低.
1.2 問題描述
具體分為兩種情況描述上下學校車的最少運營數量問題,即極限情況和一般情況.
極限情況:U學校只有1輛校車,要完成送S個學生上學.該情況下校車的數量最少,校車的利用率最高,空載率最低,校車公司收益最大,但是每個學生的到校時間最晚,最早上車的學生乘車時間最長.
該問題可以抽象為在m個乘降站中選擇某一個特定的乘降站作為起點,將學校作為終點,選擇一條能夠遍歷所有乘降站的最短的校車行駛路線.考慮到該情況下路線具有雙向性,該情況下上學的最優路線也是放學送學生回家的最優路線.因此時這個問題就是一個單源點的頂點遍歷最短路徑問題,可以采用本文提出的SBLS算法求解.解題時將其源點和終點互換,避免m個乘降站作為源節點時的m個方案之間的比較,使得運算時間降低m倍.
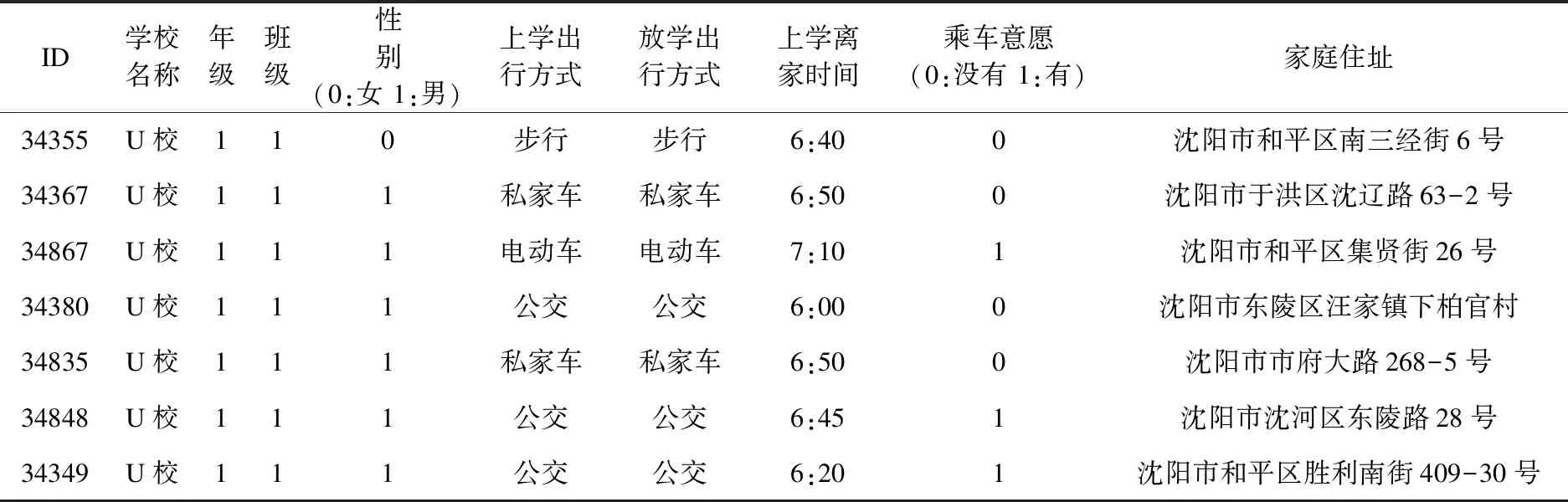
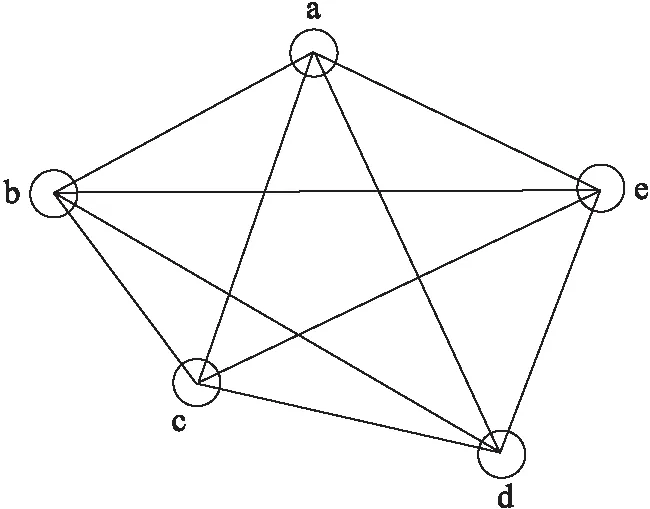
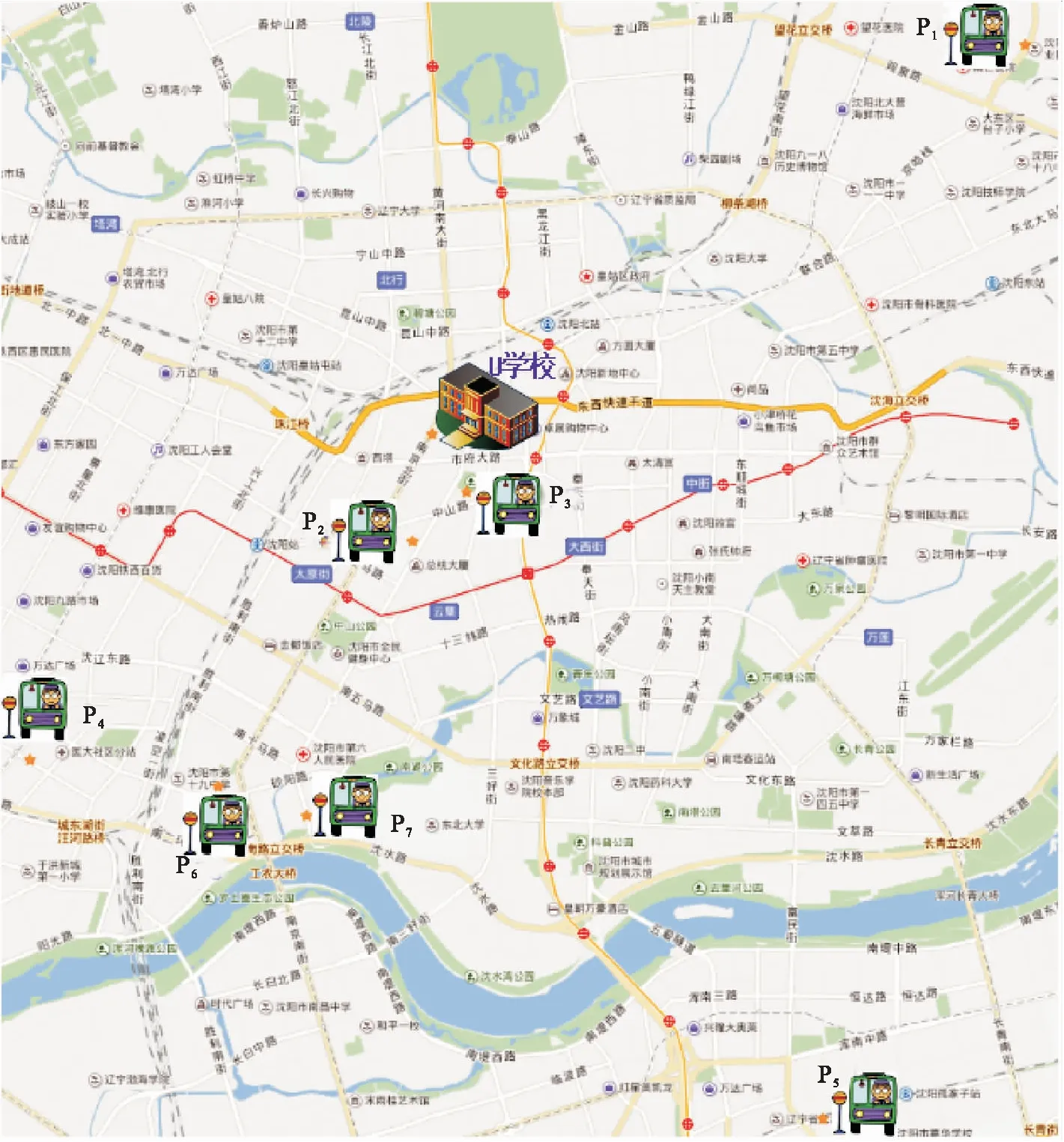
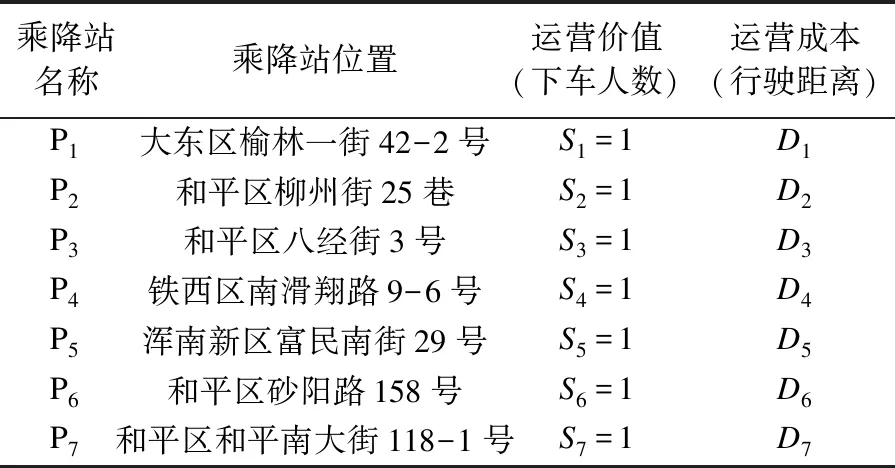
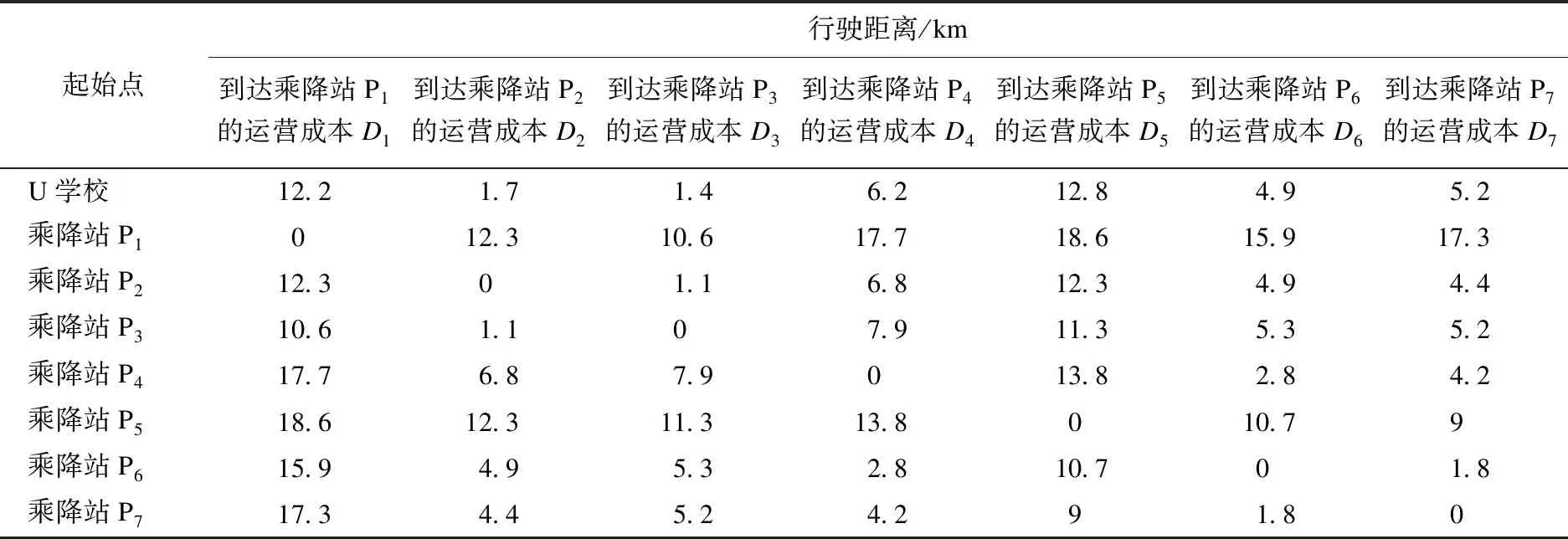
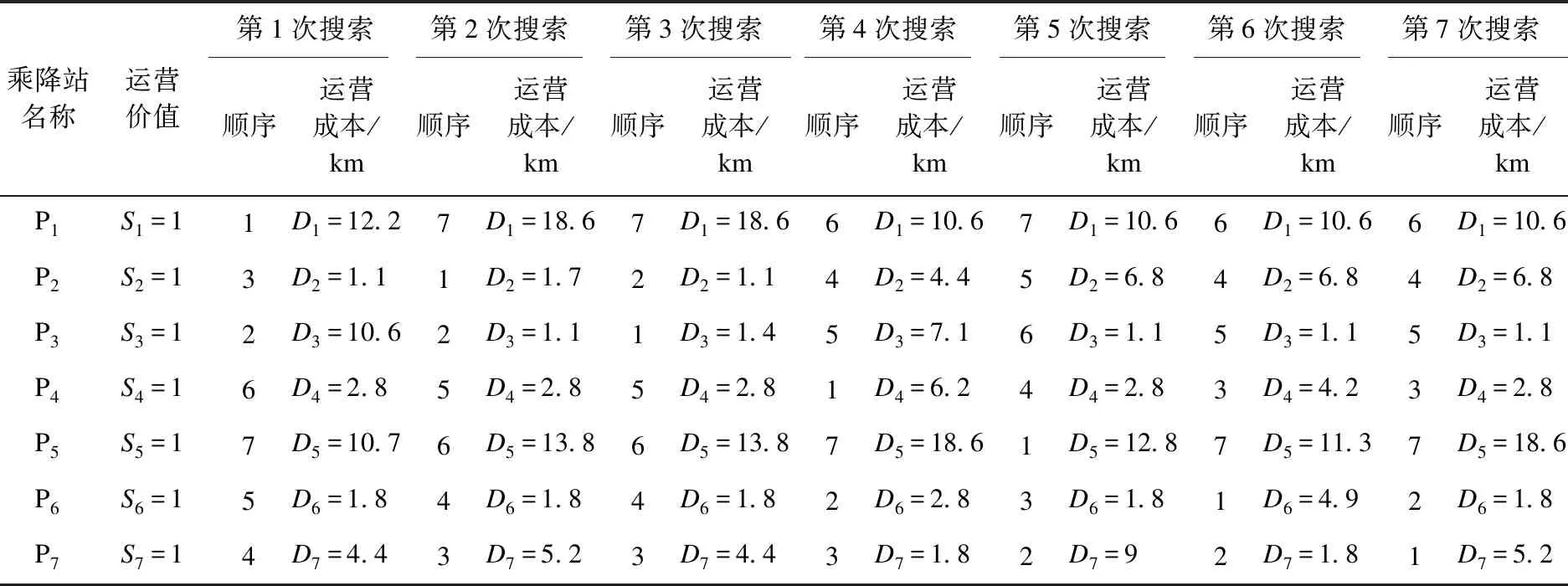
一般情況:U學校有n輛校車,接送S個學生放學上學,此時n 該問題首先需要在m個乘降站中選擇n個乘降站作為n輛校車的起始出發點.考慮到每個乘降站都有可能成為校車的出發點,這使得計算復雜度增加m!/((m-n)!n!).該情況下路線仍然具有雙向性,上學時的最優解也是放學時的最優解,可以將上學問題轉化為放學問題,將學校作為起點,將m個乘降站中的n個乘降站作為終點. 此時該問題可以抽象為:每輛校車都有一個最遠的行駛距離,保證最后下車學生能夠在給定時間內按時到家;每輛校車最多載學生30人;第1輛校車選擇運送某個學生時,該校車的座位數量和剩余行駛距離都會減少,第1輛校車要在保證運載人數和最遠的行駛距離都不超標的條件下,盡可能的多挑選學生乘坐該校車.此時問題就變成了一個0-1的背包問題[8],下面采用SBGS算法來解決該問題. 第1輛校車采用SBGS算法挑選完其運載的學生之后,第2輛校車從剩余的沒被第一輛校車選走的學生中再次采用SBGS算法挑選第2輛校車要運載的學生.以此類推,直到第n輛校車挑選完最后一個學生為止.此時n就是所需的最少的校車數量. 通過SBGS算法可以有效地確定出每輛校車應該運送的學生是誰,再根據這些學生到達的乘降站,采用SBLS算法獲得該校車遍歷這些乘降站的最短行駛路徑. 上學時校車的最少運營數量問題是放學校車最少運營數的等價反問題,其采用放學校車最少運營數給出的求解方法. SBLS算法用來確定地圖上學校為起點某個乘降站為終點的最短路徑,并且該路徑必經過特定的其他頂點. SBLS算法解決的問題是基于圖論的,但是并不是圖論中的經典問題.乘降站和學校都被視為一個圖G的頂點V,連接乘降站和學校道路被看成是該圖G的邊E.每條邊無方向但是有權重W,權重W就是該路徑的長度.該圖G上任意兩個頂點V有邊E,地理因素決定所有頂點V都是相鄰頂點,例如:所有的乘降站之間、學校和乘降站之間在地理上都會有一條可以行使的路線,即地理上任何兩個地點之間都會有至少一條道路連通[9]. 綜上,圖G可以看成是一個無向有權重全連通圖,SBLS算法就是在圖G中找到一條以學校為起點,能夠遍歷所有其他頂點的最短路徑. SBLS算法解決的問題就是一個單源點的遍歷最短路徑問題,求得從學校途經指定的所有乘降站的一條最短的遍歷路徑. U學校需要n輛校車完成學生放學后送學生回家的任務.第一輛校車C1要在U學校的m個乘降站選擇e1個乘降站作為校車C1負責到達的乘降站.校車C1一旦選擇了m個乘降站中的e1個乘降站,則選擇的e1個乘降站分別是:P1,P2,P3,…,Pi,…,Pe1-1,Pe1. 校車C1創造的總的運營價值(下車人數)V1=S1+S2+S3+…+Si+…+Se1-1+Se1. 校車C1消耗的總的運營成本(行駛距離)G1=D1+D2+D3+…+Di+…+De1-1+De1. 校車C1要在m個乘降站選擇e1個乘降站使校車C1創造的總的運營價值V1盡可能的大.V1越大表示校車C1裝載的學生人數越多,即充分利用了每輛校車,但是V1一般要≤20人或者≤30人. 同時,校車C1要在m個乘降站選擇e1個乘降站,使消耗的總的運營成本G1≤L.L是一輛校車的一次行駛最大距離,規定校車一次行駛最大距離L是為了保證家距離學校很遠的學生也能夠在放學后的1 h內到家.L的具體設定取決于實際情況,由家長和學校共同商討確定. 問題簡化:1個學校,n輛校車,m個乘降站. 校車C1要在m個乘降站選擇e1個乘降站,使校車C1消耗的總的運營成本G1≤L,同時創造的總的運營價值V1盡可能的大. 校車C2要在m-e1個乘降站選擇e2個乘降站,使校車C2消耗的總的運營成本G2≤L,同時創造的總的運營價值V2盡可能的大. 校車C3要在m-e1-e2個乘降站選擇e3個乘降站,使校車C3消耗的總的運營成本G3≤L,同時創造的總的運營價值V3盡可能的大. 以此類推,校車Ci要在m-e1-e2-e3-…-ei-1個乘降站選擇ei個乘降站,使校車Ci消耗的總的運營成本Gi≤L,同時創造的總的運營價值Vi盡可能的大. 以此類推,校車Cn要在m-e1-e2-e3-…-en-1個乘降站選擇en個乘降站,使校車Cn消耗的總的運營成本Gn≤L,同時創造的總的運營價值Vn盡可能的大. 該問題本質上屬于0-1背包問題,可以采用動態規劃的方法求解. 實驗選取沈陽市某校 U為例,學生數據為該學校周邊范圍內就讀于該校的學生信息.所獲得的數據信息見表1.信息包括10個屬性:學生的ID(5位數字)、學校名稱(本實驗以U 校為例)、年級、班級、性別、上學出行方式、放學出行方式,上學離家時間、乘校車意愿、家庭住址.其中乘校車意愿中 0 表示不愿意乘坐校車,1 表示愿意乘坐校車,后續數據對其統計篩選. 表1 U校學生信息表Table 1 Student information of U school 3.2.1 SBLS算法 如圖1所示,假設學校U是圖G的頂點a,4個乘降站分別是圖G的4個頂點b、c、d、e.圖G是全連通圖,5個頂點之間都有連通的路徑,原因是地理上任意兩個點之間都有道路的連通. 每條路徑都有權重,例如連接頂點a和頂點b之間的邊Eab的權值可以通過使用SBLS算法獲得,即SBLS中每條邊的權值都是通過最短路徑算法計算出來的,表示兩個頂點之間的最短路徑的長度.校車從頂點a出發,遍歷4個頂點b、c、d、e. 如圖2所示,全連通圖G中有5個頂點,因此圖G中有10條邊.抽象圖G中邊的幾何長度不表示權重,每條邊的權重可以通過前面的SBLS算法求出,結果如表2所示,例如邊Eba的權重為1.1 km. 圖2 U學校和4個乘降站在圖G中抽象位置關系Fig.2 Abstract positional relationship in figure G of U school and 4 boarding and landing stations 表2 全連通圖G中每條邊的權重Table 2 Weights of each edge in the fully connected graph G km 圖G中以頂點a為源點,遍歷頂點b、c、d、e的路徑共有(5-1)!=24條(見圖3). SBLS算法基于Branch Bounding思想以廣度優先的方式搜索圖3中的樹,找到最優路徑所在的分支,即權重之和最小的分支[10].在實現SBLS的過程中可以引入堆棧存儲的方式來增加SBLS的運行效率.把搜索過程看作是對一棵樹的遍歷,那么剪枝就是將樹中不能得到最優解的結點剪掉[11]. SBLS算法從G的源點a和空隊列開始.結點a被擴展之后,其子結點b、c、d、e被依次插入隊列當中;然后取出隊頭元素,進行下一步擴展,保證每一次擴展時,源點a到當前節點的和都是最小.具體的解空間圖如圖3所示. SBLS算法過程:SBLS算法先從源節點a開始擴展,4個子結點b、c、d、e被插入到隊列當中,如表3所示. 表3 SBLS算法的活節點隊列Table 3 Live node queue of SBLS algorithm 取出結點a-b,它有3個子樹.因為Ecb=1 km 表4 SBLS算法的活節點隊列Table 4 Live node queue of SBLS algorithm 取出頭結點a-c,它有3個子樹.因為Ecb=1 km 表5 SBLS算法的活節點隊列Table 5 Live node queue of SBLS algorithm 重復上面操作直到隊列為空. 3.2.2 SBGS算法 下面以校車C1為例,給出校車C1在m個乘降站里選擇e1個乘降站的具體計算方法. V1(Pi,G1)= (1) (2) Pi表示C1可選的乘降站為Pi,…,Pe1-1,Pe1;G1表示校車C1消耗的總的運營成本(行駛距離);V1(Pi,G1)表示乘降站為Pi、運營成本為G1時校車C1創造的總的運營價值(下車人數). 以學校U為例,學校U有7名學生乘坐校車C1回家,該7名學生的乘降站位置選擇方法如前文所述,共有7個乘降站,如圖4所示.7個乘降站的地理位置、運營價值、運營成本見表6. 圖4 U學校和7個乘降站的位置Fig.4 Location of U school and 7 boarding and landing stations 表6 7個乘降站的地理位置、運營價值和運營成本Table 6 Geographical location,operational value and operating costs of the seven boarding and landing stations 每個乘降站有1名學生下車,因此校車C1途經每個乘降站的運營價值都是1.校車C1為了到達某個乘降站Pi而行駛的距離Di取決于校車C1的前一個途經的乘降站Pi-1.因此,校車C1到達乘降站Pi的運營成本(行駛距離)Di是一個動態變量,取決于出發點,如表7所示. 表7 不同起始點的7個乘降站的動態運營成本Table 7 Dynamic operating costs of 7 boarding and landing stations with different starting points 校車C1沿著不同順序到達7個乘降站時,所消耗運營成本將會發生動態變化.到達同一個乘降站也會隨著起始點的不同而產生不同的成本.表8給出了7種順序得到的全部成本. 表8 校車C1搜索7次的每一次運營成本Table 8 Each operating cost of the school bus C1 search 7 times 通過上述SBGS算法,可以得出校車C1到達哪些乘降站,這些乘降站的數量是e1,以及到達上述e1個乘降站的順序.然后再次使用SBGS算法在剩余的m-e1個乘降站中選擇出e2個乘降站作為校車C2的到達目的地,同時也獲得最短行駛路徑下的到達上述e2個乘降站的順序. 依次反復使用SBGS算法,直到所有的乘降站都被選擇完畢,則此時所需的校車數量、每輛校車負責的乘降站集合、每輛校車到達各自負責的多個乘降站的最短路徑都可以被依次求出. 針對無混載校車路徑規劃問題,查詢部分中小學校的上下學時間、學生的家庭住址和學校地址,充分調研沈陽市交通情況,綜合考慮校車運營方式和盈利方法,對實際的校車運營問題進行分析,把經典的校車路徑規劃問題拆分為校車最短路徑與最少運營數.重點關注校車數量,提出了SBLS算法和SBGS算法.實驗結果表明:運用算法后的行車距離更短,校車數量減少,達到了降低運營成本的預期效果. 采用圖論的方法,推導了不同情況下校車數量與校車路徑之間的計算關系,闡述了不同運營方式所產生的行駛距離不同的情況.對校車數量問題設定兩種情況,不同情況給出不同的算法.極限情況作為一般情況的支撐,一般情況的SBGS算法加上極限情況SBLS算法為無混載校車路徑問題、校車運營數量問題提供了解決方案. 文中在構建校車路線優化模型時沒有考慮城市交通的情況.事實上,由于校車運營時間集中在早晚的城市交通高峰期,不可避免地出現交通擁堵現象,導致校車到達不及時. 在這種情況下,一些學校調整了學校的上下學時間,在設計校車路線時做到基于學校上下學時間調整校車調度方案[12].后續將會在本研究的基礎上,考慮學校時間窗的調整,服務于錯峰上學背景下的校車路徑問題;考慮實時交通情況,做出基于實時城市交通的校車路徑規劃;結合兩種情況的有混載校車路徑規劃,進一步完善校車路徑問題在生活實際中的運用.2 算法設計
2.1 SBLS算法
2.2 SBGS算法
3 實 驗
3.1 實驗數據
3.2 實驗結果分析




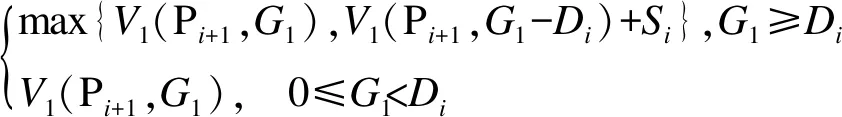
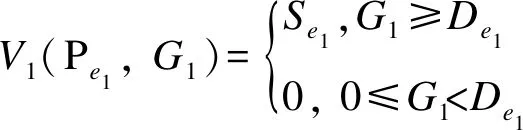
4 總 結

