多臺階渦輪軸三輥斜軋減徑量對軋制過程的影響規律研究
徐永銘, 孫寶壽*, 束學道, 徐煥磊
多臺階渦輪軸三輥斜軋減徑量對軋制過程的影響規律研究
徐永銘1,2, 孫寶壽1,2*, 束學道1,2, 徐煥磊1,2
(1.寧波大學 機械工程與力學學院, 浙江 寧波 315211; 2.浙江省零件軋制成形技術研究重點實驗室, 浙江 寧波 315211)
運用Simufact有限元軟件建立了三輥斜軋兩道次成形多臺階渦輪軸的仿真模型, 通過數值模擬分析了渦輪軸成形情況, 探究了減徑量對軋制過程中軋制力、等效應力-應變以及外圓度誤差的影響規律. 結果表明: 隨減徑量的增大, 軋件第1道次和第2道次的徑向載荷、等效應力、等效應變和外圓度誤差均呈增大趨勢. 綜合比較3種方案下的軋件成形情況, 方案2為最佳的道次減徑量分配方案, 即第1道次減徑6mm, 第2道次各臺階減徑量分別為2、9和14mm.
三輥斜軋; 多臺階渦輪軸; 兩道次; 減徑量
渦輪軸是航空發動機上的核心傳動部件, 由于高速、高溫、高壓的惡劣工作環境, 也是最容易發生故障的部位[1]. 渦輪軸的成形方法和成形質量直接影響著飛機飛行的安全以及大國航空發動機的裝備技術水平. 目前渦輪軸的加工方式仍多采用傳統鍛造工藝, 由于工藝特性, 鍛造成形的渦輪軸容易出現彎曲、偏心等缺陷, 而且表面存在嚴重的金屬折疊缺陷, 造成后續精加工切削的余量較多, 所以渦輪軸成品率和材料利用率均較低[2].
三輥斜軋的概念最早起源于蘇聯, 隨著有限元理論的日益完善, 各國學者通過數值模擬技術對三輥斜軋成形過程進行了深入研究. Pater等[3-4]對三輥斜軋成形卡車車軸進行了有限元仿真, 驗證了該工藝成形階梯軸的可行性以及通用性. 王付杰等[5]對管坯在三輥斜軋穿孔過程中的應力-應變分布及軋輥扭矩的變化規律進行了數值模擬分析, 并在實驗平臺上驗證了模擬結果. 尹元德等[6]建立了Assel三輥斜軋工藝成形薄壁管過程的有限元模型, 分析了芯棒運動方式、送進角和軋輥輾軋帶線型對軋件內螺紋缺陷的影響規律.
在現有研究基礎上, 本文基于Simufact有限元軟件建立多臺階渦輪軸三輥斜軋兩道次成形的仿真模型, 通過分析軋制過程中軋制力、等效應力-應變和外圓度誤差隨減徑量的變化規律, 選取最佳的道次減徑量分配, 以獲得最優的軋件成形方案和成形質量, 為三輥斜軋多道次軋制階梯軸的減徑量分配提供參考依據.
1 有限元模型的建立
1.1 三輥斜軋原理
三輥斜軋即是3個同向旋轉的軋輥繞軋制中心線呈120°圓周分布, 并且軋輥軸線相對于軋制中心線偏轉一定的角度(即為送進角), 故軋件在軋輥的帶動下做螺旋式前進運動. 在軋制過程中, 軋輥可以沿軋件徑向進給, 收縮孔型以達到成形階梯軸不同直徑尺寸的目的. 另外, 在實際生產中經常根據減徑量的變化, 通過外部動力牽引卡盤帶動軋件軸向運動, 從而協調軋輥的軋制速度. 圖1即為三輥斜軋原理示意圖.
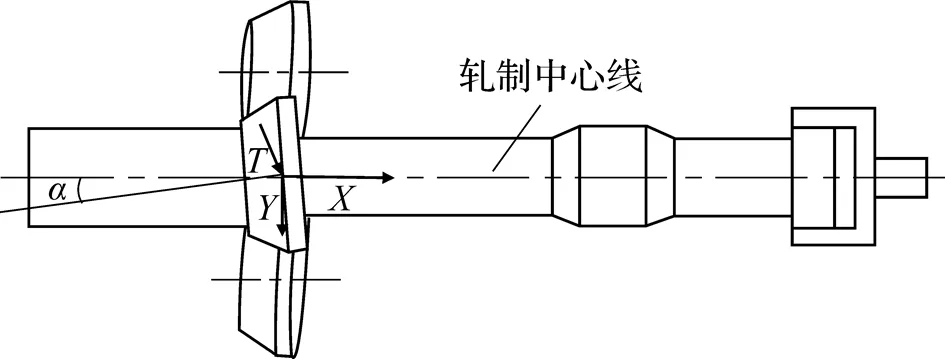
圖1 三輥斜軋原理示意圖
1.2 毛坯材料及網格劃分
如圖2所示, 仿真模型由3個相同軋輥、芯棒、卡盤以及管坯組成.
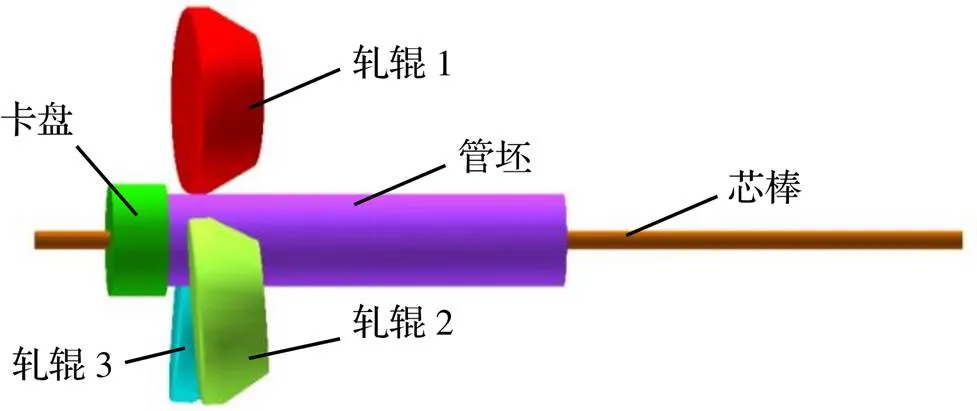
圖2 多臺階渦輪軸三輥斜軋有限元模型
為了后期開展實驗驗證的需要, 選取1:3的多臺階渦輪軸作為研究對象, 尺寸如圖3所示, 即選用外徑50mm、內徑10mm、長度230mm的管坯進行軋制, 材料為鎳基高溫合金GH4169, 本文采用的本構方程如下[7]:
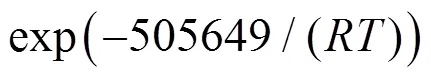
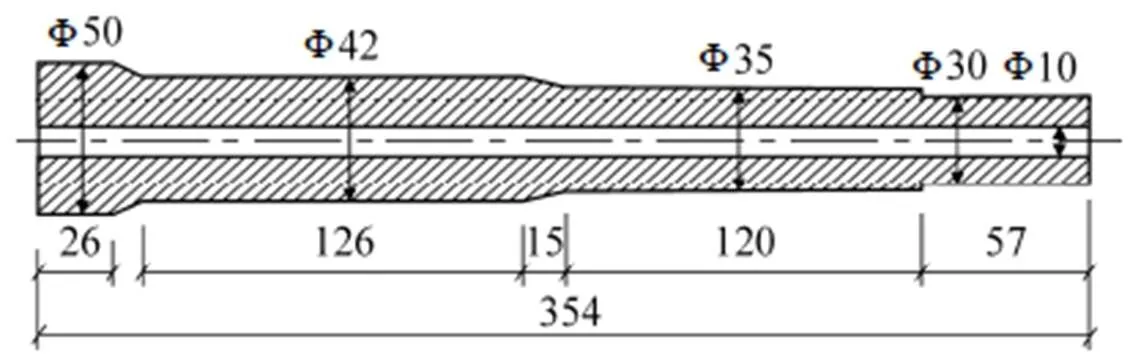
圖3 1:3多臺階渦輪軸(單位: mm)
坯料網格采用六面體自由網格進行劃分, 網格尺寸設置為3mm, 另外通過網格細化功能對軋件斷面收縮率較大的Φ30mm臺階部分進行區域細化, 細化等級選擇1級, 即細化區域網格大小為正常區域1/8, 最終坯料網格數確定為11608.
1.3 初始條件和邊界條件
在多臺階渦輪軸三輥斜軋成形過程中, 軋件主要發生塑性變形, 彈性變形量較小, 為了縮短有限元仿真時間, 故采用剛塑性有限元法[8], 將軋件定義為塑性體, 其初始預熱溫度為1050℃; 將軋輥、芯棒和卡盤定義為恒溫剛性體, 其溫度均設定為150℃; 另外設置環境溫度為20℃.
為了在數值模擬時方便設置細化區域, 根據相對運動原理, 將裝有卡盤的一端固定, 以軋輥的軸向運動代替軋件的軸向運動. 定義軋件與卡盤的接觸類型為粘結, 忽略兩者間的摩擦. 另外實際生產中常通過在軋輥表面設置溝槽來增大軋件與軋輥間的摩擦力, 減小相對滑動[9], 所以在模擬時可適當增大摩擦因子. 摩擦類型選擇系統默認(自動)模式, 軋件與軋輥間的摩擦比例因子設置為0.9, 與芯棒間的摩擦比例因子設置為0.1.
軋制過程中傳熱現象非常復雜, 主要存在熱傳導、熱對流和熱輻射3種類型的熱邊界條件[10].根據文獻[11], 設定軋件對環境的熱傳導系數為0.05kW?(m2?K)-1, 與環境的熱輻射率為0.25; 模型其他組件對環境的熱傳導系數為0.05kW?(m2?K)-1, 對軋件的熱傳遞系數為20kW?(m2?K)-1, 與環境的熱輻射率為0.25.
2 渦輪軸成形方案
表1為多臺階渦輪軸三輥斜軋模型的主要工藝參數.
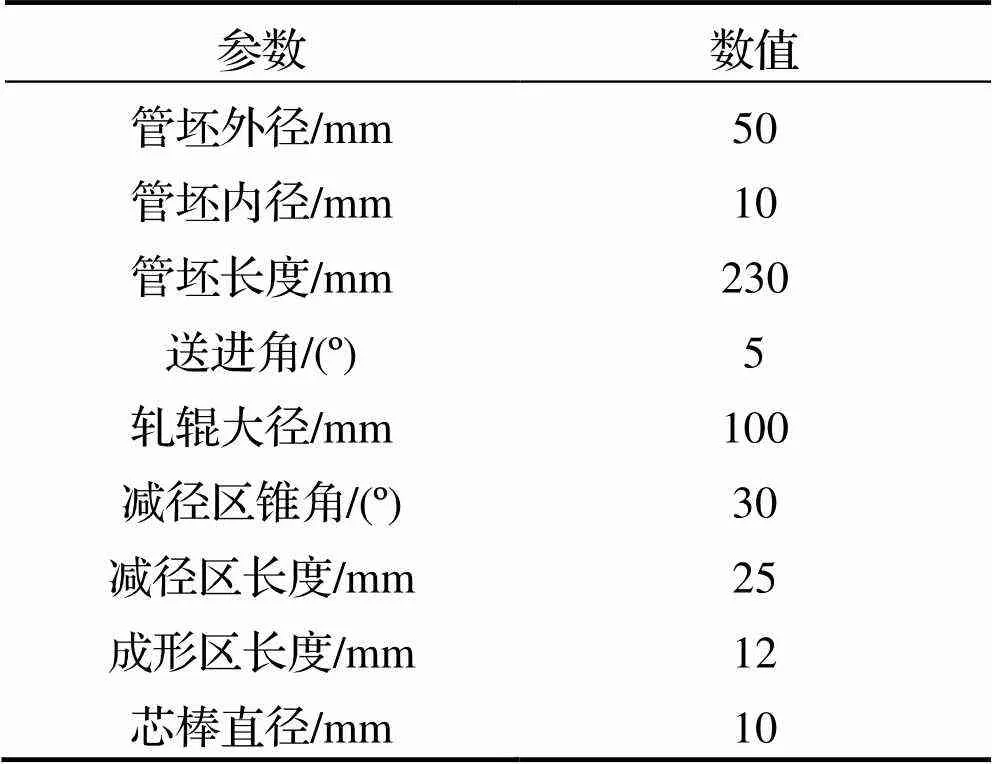
表1 模型工藝參數
由于GH4169屬于典型的難加工材料, 工藝塑性差[12-13], 經仿真試驗后發現所研究的渦輪軸一道次成形的質量較差, 而多道次軋制降低了生產效率, 增加了生產消耗, 故采用兩道次成形多臺階渦輪軸, 選取第1道次轉速80r?min-1, 第2道次轉速60r?min-1, 軸向速度均為20mm?s-1, 其渦輪軸軋制成形過程如圖4所示. 在總減徑量一定的情況下, 具體各道次分配方案見表2.
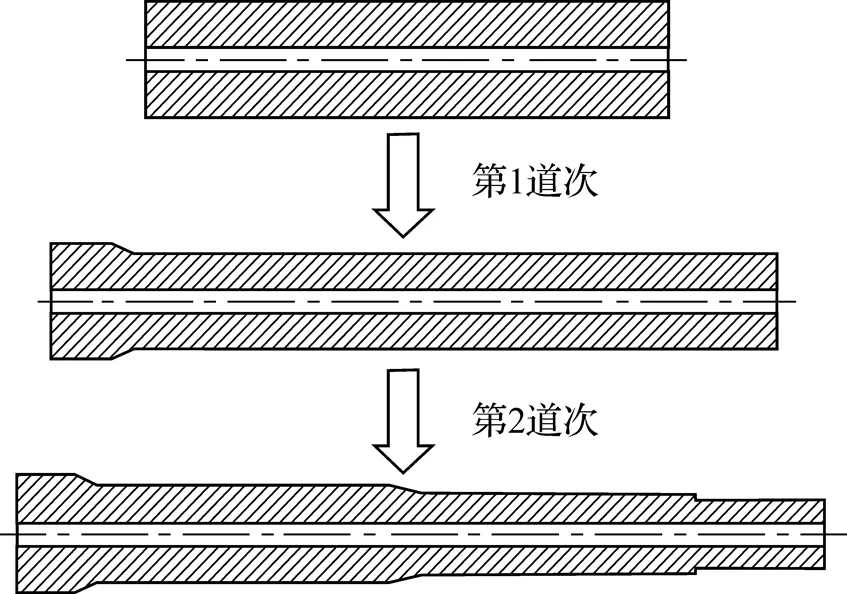
圖4 多臺階渦輪軸成形過程

表2 減徑量分配方案 mm
注: 1)該列所示各方案所對應的3個數據分別為第2道次三段臺階成形直徑42、35和30 mm的減徑量.
3 仿真結果及分析
3.1 減徑量對徑向載荷的影響
三輥斜軋是以軋輥壓縮軋件進行的塑性變形, 故主要針對軋件所受徑向載荷進行分析. 圖5為軋件在軋制過程中所受單個軋輥的徑向載荷變化情況. 從圖中可以看出, 軋輥的每次徑向進給均伴隨著載荷的急劇增加, 并以特征峰形式呈現. 在第1道次等徑段軋制時, 受固定端牽引作用的影響[14], 徑向軋制力隨軋輥沿軋制方向的移動平緩上升; 第2道次每段等徑段的長度相比第1道次明顯減小, 所以等徑段的徑向軋制力變化并不明顯. 第2道次軋制時, 因為軋輥只需對方案3中Φ42mm臺階的少量回流金屬進行減徑, 所以該段的徑向載荷相對較小. 另外, 在2個道次之間存在一段軋輥移動時間, 該段時間內軋件不與軋輥接觸, 其不受任何負載的影響.
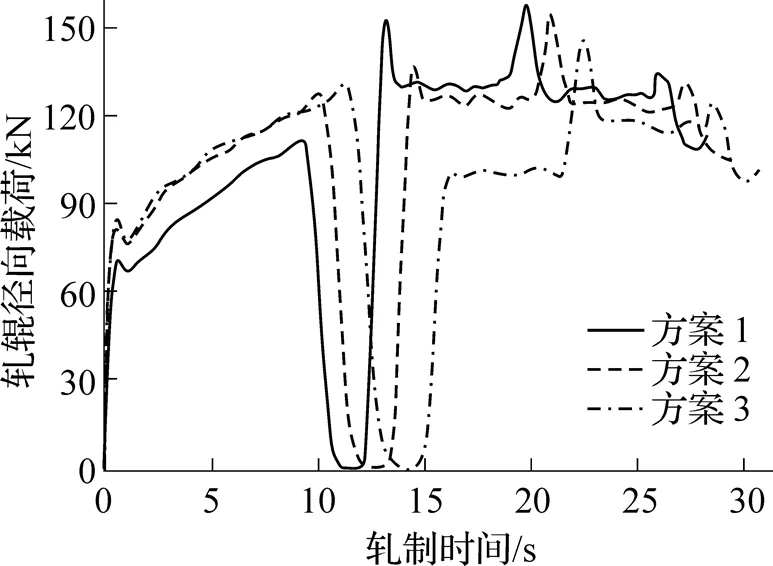
圖5 減徑量對軋輥徑向載荷的影響分布曲線
對比圖5中3種方案曲線后可以發現, 減徑量越大, 軋件第1道次和第2道次的徑向軋制力越大, 但是增大幅度卻隨減徑量的增加而明顯減小. 在兩道次軋制時, 若保證成形過程中的軋制力變化相對均勻, 則有利于軋機工作周期的運行平穩, 延長軋機部件的壽命[15], 這也是道次減徑量分配的重要依據.
3.2 減徑量對等效應力-應變的影響
利用軟件點位追蹤功能探究減徑量對軋制過程中等效應力和等效應變變化的影響規律, 即在軋件上選取節點(圖6), 分別用1、2、3、4和5表示, 其中1為軋件外表面點,5為軋件內表面點,2、3、4分別為1與5之間的等分點.
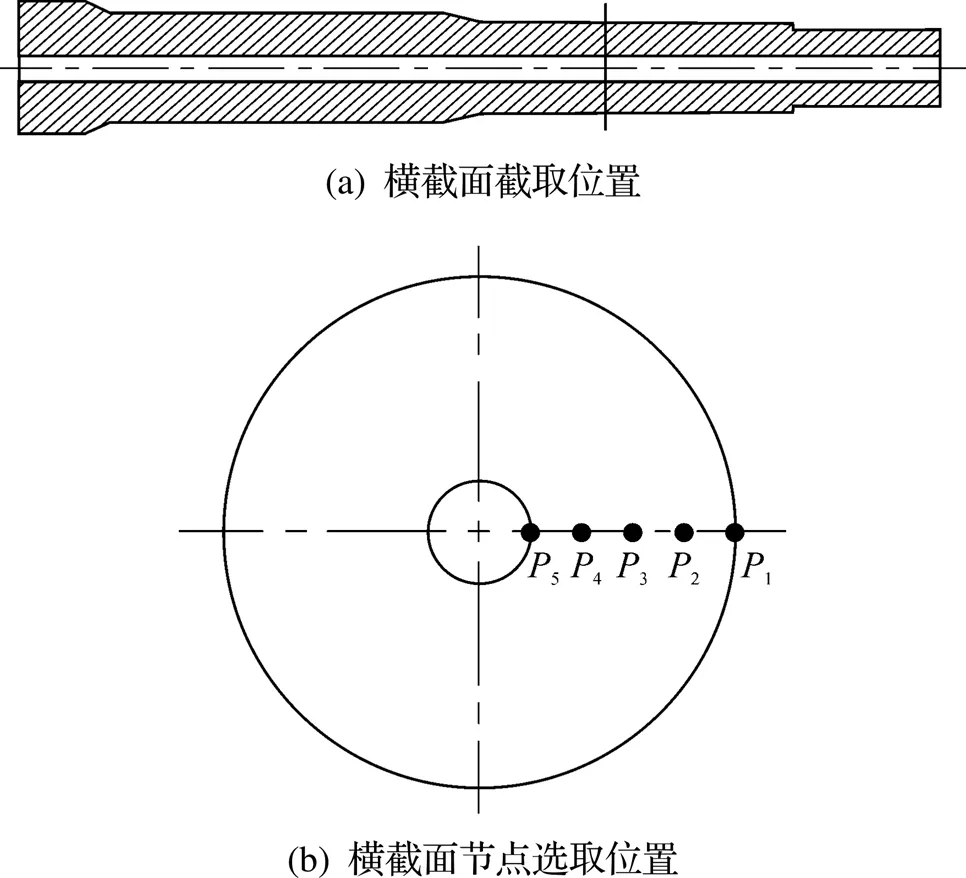
圖6 等效應力-應變追蹤節點位置分布
圖7為所選橫截面上5個節點的等效應力變化曲線. 從圖中可以看出, 隨著軋輥咬入軋件, 節點的等效應力開始緩慢增大, 當截面進入軋輥減徑區時, 各節點的等效應力急劇增大, 并在截面離開軋輥減徑區時達到第1道次的峰值, 而后快速減小, 并且第2道次的等效應力變化規律與第1道次基本一致. 但是軋件內外表面金屬軸向變形的不均勻導致第1道次軋件尾端出現凹陷現象[16], 從而在軋制時造成軋件上靠近內表面區域的等效應力突然增大. 對比截面上5個節點的曲線可以發現,1、2和3點間的等效應力變化不大,4和5點由于芯棒對軋件內的表面作用, 使其等效應力大于其余3個節點, 并且越靠近軋件內表面, 芯棒的作用越明顯.
對比圖7中3種方案曲線還可以發現, 方案1第1道次等效應力最大值為317.2MPa, 第2道次最大值為436.1MPa; 方案2第1道次等效應力最大值為337.3MPa, 第2道次最大值為393MPa; 方案3第1道次等效應力最大值為444.1MPa, 第2道次最大值為370.6MPa. 由此可知, 軋制過程中各節點的等效應力與減徑量成正比關系, 即減徑量越大, 軋件的等效應力越大.
圖8為所選橫截面上5個節點的等效應變變化曲線. 從圖中可以看出, 等效應變曲線呈現兩段式階梯狀. 軋件每道次等效應變急劇增大的時間節點與等效應力基本一致, 但是5個節點的等效應變均隨半徑的減小呈遞減趨勢, 這是因為軋件與芯棒間存在熱傳導現象, 導致軋件溫度下降, 并且越接近內表面, 溫度下降越嚴重, 最終導致4、5點的等效應變小于其余3個節點.
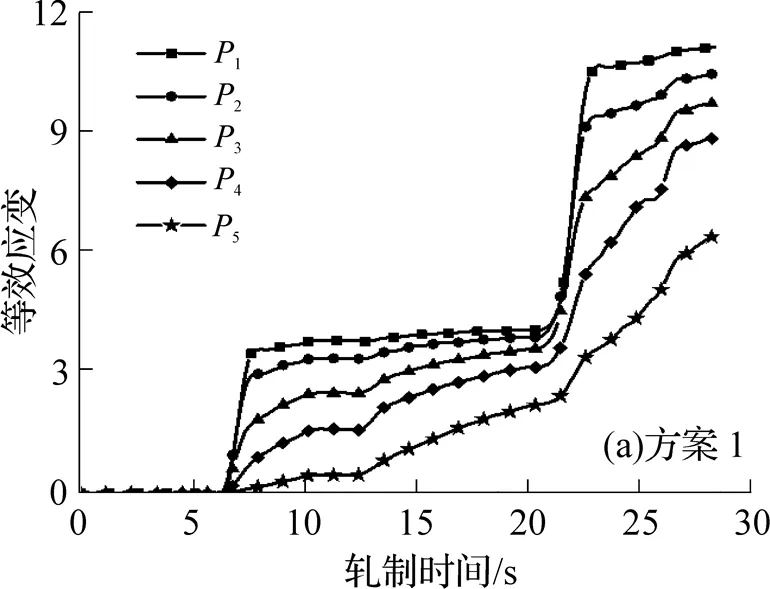
對比圖8中的3種方案曲線還可以發現, 各點的等效應變隨減徑量的增大而增大, 這與等效應力的變化規律相符. 在兩道次軋制時, 軋制過程中的等效應變均勻性也是選取方案的重要指標. 其中, 方案1第1道次等效應變增大幅度為3.91, 第2道次增大幅度為7.28; 方案2第1道次等效應變增大幅度為5.20, 第2道次增大幅度為6.49; 方案3第1道次等效應變增大幅度為7.09, 第2道次增大幅度為5.09.
3.3 減徑量對外圓度誤差的影響
分別截取第1道次和第2道次軋件上經軋輥成形的等徑段中心橫截面為研究對象, 通過Simufact軟件定義截面外表面上20個取樣節點(圖9), 并導出每個點坐標, 利用最小二乘圓法[17]計算得出3種方案成形截面的外圓度誤差.

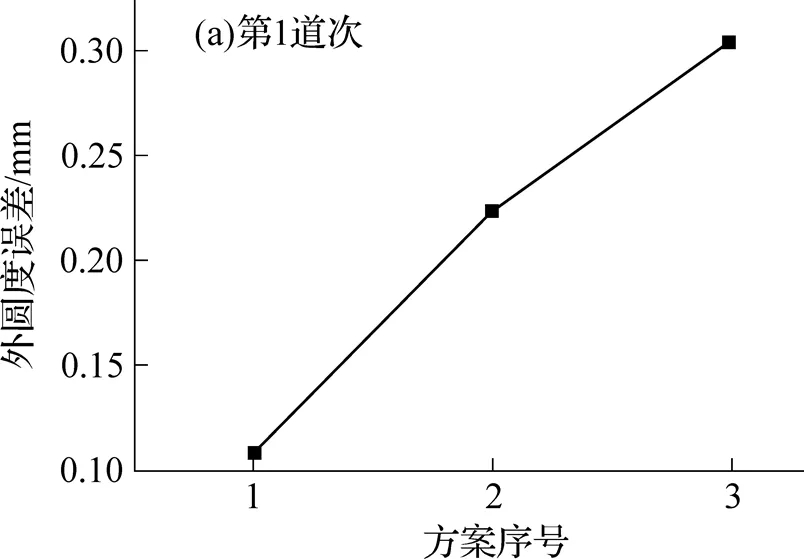
圖10為3種方案的外圓度誤差曲線. 從圖10(a)中可以看出, 軋件第1道次外圓度誤差隨減徑量的增大而增大, 但增大幅度隨減徑量的增加而減小. 由圖10(b)可知, 軋件外圓度誤差隨橫截面直徑的減小而減小, 即在軋制過程中, 所成形渦輪軸臺階直徑越小, 軋件的外圓度誤差越小, 軋件橫截面外表面形狀越接近圓形. 這是因為軋輥轉速一定時, 軋件成形直徑越小, 單位面積上軋輥輾軋的次數越多, 軋件外圓度誤差越小. 由于第2道次軋制是在第1道次基礎上進行, 第1道次的外圓度誤差會對最終成形軋件的外圓度誤差有重要影響.圖10(c)為最終成形軋件的外圓度誤差與第1道次的差值, 即為第2道次外圓度誤差相對第1道次的減小幅度, 該數值越大, 說明第2道次的外圓度誤差越小. 由圖10(c)可知減徑量越大, 軋件第2道次外圓度誤差越大, 但增大幅度減小.
4 仿真結果及分析
(1)軋輥徑向進給時, 徑向載荷均以特征峰形式變化; 隨減徑量的增大, 軋輥各道次徑向載荷增大, 但是增大幅度減小明顯.
(2)軋制過程中芯棒對軋件等效應力和等效應變的變化有重要影響; 隨減徑量的增大, 軋件各道次的等效應力和等效應變均呈增大趨勢.
(3)軋件各道次的外圓度誤差隨減徑量的增大而增大, 但是增大幅度減小; 軋件第2道次外圓度誤差隨橫截面直徑的減小而減小.
(4)綜合比較3種方案, 選取方案2作為多臺階渦輪軸三輥斜軋成形方案, 即第1道次減徑6mm, 第2道次各臺階減徑量分別為2、9和14mm. 該方案下的軋制力和等效應力-應變變化最為均勻, 外圓度誤差最小, 最終成形軋件的各臺階外圓度誤差分別為0.13、0.10和0.04mm.
[1] 崔平亮. 航空發動機低壓渦輪軸疲勞壽命計算分析[D].成都: 電子科技大學, 2014.
[2] 申秀麗, 張輝, 宋滿祥, 等. 航空燃氣渦輪發動機典型制造工藝[M]. 北京: 北京航空航天大學出版社, 2016.
[3] Pater Z, Tomczak J, Bulzak T. Numerical analysis of the skew rolling process for main shafts[J]. Metallurgy, 2015, 54(4):627-630.
[4] Pater Z, Bulzak T, Tomczak J. Numerical analysis of a skew rolling process for producing a stepped hollow shaft made of titanium alloy Ti6Al4V[J]. Archives of Metallurgy and Materials, 2016, 61(2):677-682.
[5] 王付杰, 雙遠華, 胡建華, 等. 三輥斜軋穿孔工藝的數值模擬與實驗分析[J]. 熱加工工藝, 2014, 43(9):95-98; 105.
[6] 尹元德, 李修葉, 黃浩, 等. Assel軋機軋制薄壁管壁厚螺旋性不均研究[J]. 鋼鐵研究學報, 2018, 30(7):542- 547.
[7] 吳昊, 孔祥偉, 羅平. GH4169合金高溫變形過程本構方程[J]. 機械設計與制造, 2020(8):163-167.
[8] Key S W, Krieg R D, Bathe K J. On the application of the finite element method to metal forming processes: Part I[J]. Computer Methods in Applied Mechanics & Engineering, 1979, 17/18:597-608.
[9] 李立敏, 臧勇, 張占柱, 等. 摩擦狀況對銅管行星軋制過程的影響[J]. 塑性工程學報, 2009, 16(1):115-119.
[10] 李勝祗, 孫中建, 李連詩. 實心坯二輥斜軋過程三維熱-力耦合分析[J]. 北京科技大學學報, 2000, 22(1):52- 55.
[11] 尹元德, 楊青青, 王純凱, 等. 薄壁無縫鋼管頂管過程拉凹缺陷研究[J]. 鋼鐵研究學報, 2019, 31(5):460-467.
[13] 朱德彪, 束學道. 工藝參數對楔橫軋GH4169合金軸類件力能參數的影響[J]. 塑性工程學報, 2018, 25(1):52- 59.
[14] 許暢, 束學道, 朱穎. 高鐵空心車軸三輥斜軋成形仿真及分析[J]. 寧波大學學報(理工版), 2018, 31(4):16-19.
[15] 徐春國, 任廣升. 楔橫軋工藝兩次軋制時斷面縮減率的分配[J]. 塑性工程學報, 1999(4):102-105.
[16] 曾健, 徐春國, 任偉偉, 等. 不同端部形狀下工藝參數對楔橫軋軋件凹心深度的影響[J]. 塑性工程學報, 2017, 24(2):111-117.
Numerical simulation of multi-step turbine shaft in three-roll screw rolling on its influence by diameter reduction
XU Yongming1,2, SUN Baoshou1,2*, SHU Xuedao1,2, XU Huanlei1,2
( 1.Faculty of Mechanical Engineering & Mechanics, Ningbo University, Ningbo 315211, China; 2.Zhejiang Provincial Key Laboratory of Part Rolling Technology, Ningbo 315211, China )
The simulation model of multi-step turbine shaft in three-roll screw rolling with two-pass forming was established by using finite element software Simufact. The turbine shaft forming was numerically simulated to explore the influences of the diameter reduction on rolling force, equivalent stress-strain and external roundness error during the rolling process. The results show that with the increase of the diameter reduction, the radial load, equivalent stress, equivalent strain and external roundness error of the first and second pass also increase. The comprehensive comparison of the rolling forming conditions under the three schemes indicates that scheme 2 is the best pass diameter reduction distribution scheme. In this scheme, the diameter reduction in the first pass is 6mm, and those of each step in the second pass are 2mm, 9mm and 14mm respectively.
three-roll screw rolling; multi-step turbine shaft; two-pass; diameter reduction
TG335.11
A
1001-5132(2021)04-0055-06
2020?06?28.
寧波大學學報(理工版)網址: http://journallg.nbu.edu.cn/
國家自然科學基金(51975301); 浙江省自然科學基金(LZ17E050001); 寧波市“科技創新2025”重大專項(2020Z110).
徐永銘(1995-), 男, 江蘇南通人, 在讀碩士研究生, 主要研究方向: 塑性成形工藝與裝備. E-mail: 15162855534@163.com
孫寶壽(1960-), 男, 江蘇泰興人, 副教授, 主要研究方向: 塑性成形工藝與裝備. E-mail: sunbaoshou@nbu.edu.cn
(責任編輯 章踐立)

