折疊鏈條下落過程的動力學分析*

張麗穎，林金妮，吳臆洋，邱為鋼

(湖州師范學院理學院,浙江 湖州 313000)

1 引言

鏈條下落問題是中學物理奧賽的一種常見題目，文獻[1]中的第28 題“百變柔軟繩”，和文獻[2]中的例題4-6，都提到了同一模型：一個質量均勻分布的繩子(鏈條)，折成兩半，盡量靠近,稱為折疊鏈。折疊鏈左半部分的上端固定，右半部分的上端（稱為自由端）靜止釋放。那么，這個自由端是如何下落的？文獻[1]和[2]都假設自由端是做自由落體運動，基于這種前提，計算得到了折疊鏈下落過程中固定端受到的拉力。這樣的假設對嗎？

檢驗一個物理假設是否正確最便利的方法是做實驗。通過簡單的對比實驗，將U 形鏈右端和一個小鋼球，在同一高度上同時釋放。拍攝下落視頻，比照兩者下落到最低點所需的時間。多次實驗表明：折疊鏈自由端下落，比自由落體運動更快。文獻[2]的作者考慮到該問題后，在書的第二版（文獻[3]）中對折疊鏈下落模型進行修改，在折疊鏈右端固定（系）一個小球（重物），假設體系在下落過程中機械能不變，由此可得到小球的運動方程。在理論方面，已有研究表明當把鏈條（繩子）離散化，即看作是N 個通過光滑的鉸鏈鏈接且質量均勻分布的桿時，可直接得出N 個桿的運動方程（質心和轉動）并進行數值求解。當桿數目N 取40 時，理論數值計算也發現折疊鏈的自由端比自由落體下落的快。實驗和（離散化后的）模擬都表明，折疊鏈的自由端下落不是自由落體運動。

在此基礎上，本文將從理論和實驗兩方面對折疊鏈下落運動進一步展開探究。在假設折疊鏈下落機械能不變的前提下，建立動力學模型得出鏈條自由端的運動方程。將理論與實驗結果進行分析對比，研究不同初始情況下折疊鏈自由端下落距離隨時間的變化關系。

2 理論推導

設折疊鏈整個長度為L、質量為M，其中鏈條(a)部分下落,(b)部分靜止不動，中間鏈接部分忽略不計，如圖1 所示：

圖1 折疊鏈下落示意圖

以左端固定端為原點，設自由端的坐標是y，左右兩端鏈條的長度分別為Lb和La，質心分別為Ca和Cb，其中Po為鏈條靜止下垂時的質心位置。

由圖可知：

同時總的鏈條長度不變，則

由此計算得到

鏈條左右兩端的質量為

可得左右兩段鏈條質心的坐標為

為方便計算，勢能零點取為整個鏈條完全靜止下垂時候的質心坐標ypo= -L/2處。由此得到左右兩段鏈條的重力勢能Ua(y)和Ub(y)為

設起始時刻鏈的自由端位于yo處，此時鏈的總勢能為

假設鏈條右邊下落部分，整體以自由端的速度v(y)一起下落，那么這部分的動能為

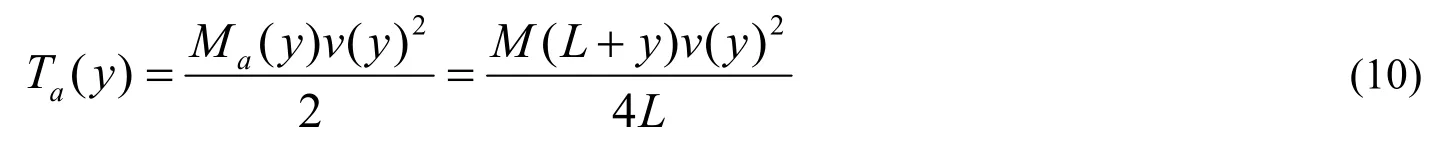
假設落鏈的機械能不變，得到

把公式(10)代入(11)式中，計算得到折疊鏈自由端的下落速度大小為

在下落過程結束快結束時,(13)式右邊根號下分母L+y趨向與零，速度發散。說明這個模型在下落末端失效。從(12)式中可以得到理論下落時間：

這個時間是有限的，不會發散。

3 實驗對比

3.1 實驗模擬

取一段大約長為一米的鏈條，用釘子將其中一端固定在泡沫塑料板上進行實驗。為了便于測量、對比讀出實際距離值，板上貼有長度標度的白紙。從固定端到自由端的長度L= 85.2厘米。起始時，自由端可以高于、等于或者低于固定端，如圖2 所示:

圖2 固定端和自由端不同高度下的釋放時刻

對于同一高度，實驗使用幀率為240fps 的高速攝像；對于不同高度，使用幀率為120fps 的高速攝像。fps的意思是frame per second，即1 秒鐘能拍攝多少張（幀）畫面,所以相鄰圖片的時間間隔為幀率的倒數分之一秒。用視頻軟件KMPPlayer，逐幀提取圖片。對于同一高度幀率為240fps 的視頻，每隔2 幅圖片進行測量，得出距離數據的時間間隔為 Δt= 3/240= 0.0125秒。對于不同高度，每幅圖片都測量，得出距離數據時間間隔為 Δt= 1/120秒。

3.2 擬合對比分析

針對三種折疊鏈條下落情況，根據式(12)理論模擬出不同情況下鏈條自由端下落位移和時間的圖像關系后，通過實驗測量出鏈條下落時圖片中鏈條自由端的位移，并將測量點繪制于y-t 圖像當中。利用Mathematica軟件將理論圖像和實驗結果相擬合，以便于更加直觀、清晰的對比理論值與實際值并加以分析。

對于同一高度，(12)式中的yo=0，理論下落時間是0.353 秒。數值求解(12)式，得到的自由端下落曲線（實線），與實驗數據（三角形符號）和自由落體運動（虛線）對比如圖3 所示：

圖3 起始自由端與固定端同一高度時的y-t 圖

對于高于固定端10 厘米，(12)式中的yo= 0.1，理論下落時間是0.373 秒。數值求解(12)式，得到的自由端下落曲線（實線），與實驗數據（三角形符號）和自由落體運動（虛線）對比如圖4 所示：

圖4 起始自由端高于固定端時的y-t 圖

對于低于固定端10 厘米，(12)式中的yo=-0 .1，理論下落時間是0.332 秒。數值求解(12)式，得到的自由端下落曲線（實線），與實驗數據（三角形符號）和自由落體運動（虛線）對比如圖5 所示：

圖5 起始自由端低于固定端時的y-t 圖

通過對比圖3、4、5 可以看出，在理論下落時間的百分之八十之內，實驗數據基本落在理論曲線上。在理論下落時間百分之六十之內，實驗數據、理論曲線和自由落體曲線，三者基本吻合。這說明下落早期，自由端可以近似看作自由落體，但不是嚴格理論意義上的自由落體。區別最大的是下落過程的末期，無論實驗還是數值模擬顯示，最下面部分的鏈條不再是直線形，而是折線形，存在水平方向的運動。理論模型(12)式中，沒有考慮到這部分的橫向動能，所以會出現末期下落速度發散的情形。

4 結論

假設下落過程中鏈條還是折疊的，即兩段線段的聯合體，左段靜止，右段整體下落，且機械能守恒（不變），由此得到了右段最上端（自由端）的下落方程。這個運動方程并不是自由落體運動方程。三種實驗數據基本和理論曲線重合，但這也并不能說明鏈條下落過程中機械能嚴格守恒，這有可能是湊巧，也可能有更深刻的機理，正如文獻[4]中所探討的，有待進一步展開研究。