基于小波稀疏的全息顯微成像研究

顧鵬翔，楊 波，宗 卉

（上海理工大學 光電信息與計算機工程學院，上海 200093）

引 言

顯微成像是一門比較成熟的技術，而無透鏡全息顯微鏡則是一項新興的，具有廣闊前景的計算成像技術。無透鏡全息顯微鏡沒有復雜的光學透鏡系統，是通過全息成像[1]、圖像重建技術以及圖像傳感器的使用來實現的，因此結構簡單、輕巧、成本低，對于遠程醫療、野外檢測、高校課堂實驗這些實時的應用場景需要比較短的處理時間的生物檢測等方面有著重要的意義。

為了使成像結構盡可能緊湊，將參考光和物光在同一方向上共同傳播，并用數字圖像傳感器陣列記錄這兩束光產生的干涉圖樣的強度。由于記錄的全息圖像只包含了復雜場的強度信息，因此光在反向傳播過程中將在原始圖像上產生偽影。同離軸全息結構不同，離軸全息可以通過角譜傳播去除偽影，而偽影將會對像質產生很大的影響。由于數字全息顯微鏡中樣本到傳感器的距離很小，樣本和傳感器的視場大小是相同的，因此，偽影的影響將進一步放大。在數字全息術中，可以通過施加偽影不滿足的物理約束來消除偽影，基于這種約束，通過迭代以減少錯誤算法來實現[2]。對于單個物體，這種方法所需的全息圖的測量很簡單，但是在處理密集連接的樣本（例如血液紅細胞、病理學切片等）時，會帶來很大的挑戰[3]。為了解決這一問題，需要進行多次多樣的測量，例如樣本到傳感器的距離、照明角度、波長等。然而，之前的研究表明，對于病理學的切片或者生物組織等密集連接的樣本，需要進行過度采樣[4]。例如，在對血液紅細胞進行多高度測量時，通常需要8幅，甚至更多的具有不同高度（樣本到傳感器距離）的全息圖才能得到高質量的重建圖像。這不僅增加了測量的數據，也增加了處理的時間。基于上述問題，提出一種基于小波稀疏化的全息顯微成像技術。

對于生物樣本，可以在某些小波域進行稀疏表示，用基于小波域的稀疏約束進行圖像重建以減少所需全息圖的測量，并且得到像質比較好的圖像。實驗表明，對于緊密連接的生物樣本（例如血液紅細胞、病理切片等），三個不同的樣本到傳感器距離的全息圖就能實現迭代重建。

本文所述的稀疏約束方法同之前報告中的壓縮全息有很大的不同。對于孤立的物體，自由的空間傳播本身就是一種有效的壓縮感知的編碼機制，可以從傳統的低采樣預測出高維度的數據。而本文所述的基于小波的稀疏重建是對密集連接的樣本而不是孤立的，并且可以在20 mm2的視場（等于傳感器的范圍）實現對血液紅細胞樣本的顯微成像。

這種基于稀疏的圖像重建方法可以擴展到其它相關的顯微鏡成像中，例如多角度或者多波長的圖像重建[5-8]。還可以結合最近比較熱門的超分辨寬視場技術以及多路復用彩色圖像技術，可以進一步減少全息測量的數量，利用一些新的算法，可以實現高效便捷的顯微技術。

1 基本原理

1.1 稀疏表示

稀疏表示是近年來圖像處理和模式識別方向的研究熱點。信號稀疏表示的目的就是在給定的超完備字典中用盡可能少的原子來表示信號，可以獲得信號更為簡潔的表示方式，從而更容易地獲取信號中所蘊含的信息，方便更進一步對信號進行加工處理，如壓縮、編碼等[9]。信號稀疏表示方向的研究熱點主要集中在稀疏分解算法、超完備原子字典和稀疏表示的應用等方面。信號稀疏表示的兩大主要任務就是字典的生成和信號的稀疏分解。對于字典的選擇，一般有分析字典和學習字典兩大類。常用的分析字典有小波字典、超完備DCT字典和曲波字典等，常用的學習字典的方法有MOD算法、K-SVD算法等。一個信號可以稀疏地表示為冗余字典中少量原子的線性組合。

字 典D=(d1,d2,···,dm)∈Rn*m(m＞n) ，其 中每一個原子dj∈Rn，信號x∈Rn可以表示為

式中a=[α1,α2,···,αm] 為分解系數，當a中非零元素的數目僅為k個時，稱a為k稀疏信號，或者稱信號x在字典D下是k稀疏信號。若m=n，字典D為完備字典，字典內的各個原子相互正交；若m＞n時，字典D是冗余的；若m?n，字典D為過完備字典，字典內的各個原子并不是相互獨立的[10]。

圖1形象地表示了稀疏表示的基本原理。

圖1 稀疏表示的基本原理Fig.1 The operation principle of sparse representation

1.2 角譜傳播理論

在獲得了一系列寬視場、低分辨率，具有不同樣本到傳感器距離的全息圖后，這些全息圖的信息可以表示為

式中： λ 為照明波長；n為折射率；zi為樣本到傳感器之間的距離；o為對象函數；A為參考平面的振幅。ASP[.] 算子表示自由空間傳播的角譜，其計算方法是將信號進行空間傅里葉變換，然后乘光學傳遞函數H(vx,vy;λ,n,zi) ，其中光學傳遞函數為

式（3）相當于一個低通濾波器，vx與vy為空間頻率之后進行傅里葉反變換，全息圖的強度Ii(x,y)是通過傳感器獲取的，它的采樣間隔和像素間距是相對應的。為了使圖像恢復的更好，還需要進行數字注冊，使得全息圖的相位等信息都是相關的[11]。

2 算法步驟

2.1 總體方法

首先用無透鏡全息顯微鏡獲得3幅初始圖像，通過角譜傳播理論，得到恢復的初始圖像，再進行小波稀疏處理，得到高分辨率的圖像。為了評價3幅圖的恢復效果，將8幅圖通過多高度迭代的算法恢復作為對比[12]，用SSIM算法比較相似度。

2.2 基于迭代的多高度恢復算法

這種方法是一種錯誤減少算法，利用不同高度的全息圖作為一種物理約束，使得圖像在每一次迭代中進行不斷的校正。如果將距離CCD傳感器最遠的全息圖看做第1幅圖的話，傳播到第2幅圖時進行振幅約束，這里的振幅是得到的全息圖強度的平方根，此時，全息圖得到了更新，以此類推，直到傳播到最后一個全息圖（第8幅或者16幅）；到達最后一幅圖后，進行反向傳播，同樣將振幅不斷進行更新，直到回到第1幅圖完成第1次迭代。此算法通常需要迭代30次或者達到收斂標準后停止。此算法在基于稀疏的圖像重建算法當中作為初始的輸入，之后再進行稀疏約束等操作[13]。

2.3 基于小波稀疏的多高度恢復算法

基于小波稀疏的多高度恢復算法流程圖如圖2所示。

圖2 基于小波稀疏的多高度恢復算法流程圖Fig.2 Flowchart of multi-height recovery algorithm based on wavelet sparsity

此算法的基本思路參考圖3所示。

圖3 多高度恢復算法Fig.3 Multi-height recovery algorithm

第一步：對3幅不同高度的全息圖進行正向角譜傳播，物理約束后，振幅得到校正，進行反向角譜傳播，最終回到物平面，得到較高分辨率的全息圖，作為下一步的輸入。

第二步：將上一步結果進行小波正變換，得到一系列小波系數，此時，還不認為是稀疏的，需要進一步稀疏化。

第三步：確定稀疏域，并不斷更新稀疏域的振幅，這里需要保證小波系數中大的值不變，同時更新其余的系數，將系數值很小的變為零。

第四步：減少稀疏域以外區域的錯誤，通過放縮來調節系數的大小。

第五步：在小波域中，對圖像進行閾值去燥處理，最后，進行小波反變化。不斷重復以上步驟，直到收斂為止[14]。

2.4 評估成像質量

運用SSIM算法對基于小波稀疏的恢復圖像進行像質評估[15]。SSIM算法是基于結構相似性的圖像質量評價，結構性表現在圖像的像素間存在著很強的相關性，而大多數的質量評估方法是使用線性變換來分解圖像信號，例如，均方誤差（MSE）、峰值信噪比（PSNR）等，不涉及相關性，因此，這種方法可以更加直觀的來比較失真圖像與參考圖像結構的相似性。

SSIM測量系統是通過檢查圖像的對比度、亮度、結構之間的關系來獲取信息。其中，圖像的對比度是通過標準偏差 σp來評估的，其表達式為

式中：N為分塊總數，利用的是滑動窗將圖像分塊；xi、yi分別為x、y方向的像素指數； μp代表第p幅圖（即Up）的亮度。

結構是通過計算兩個圖像的協方差 σ1,2來評估的，其表達式為

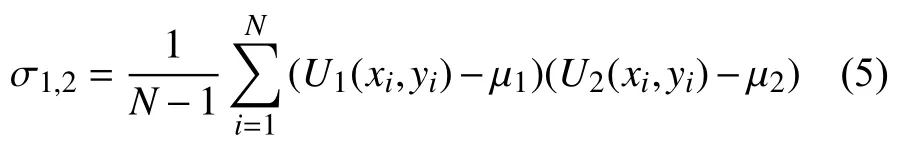
根據以上可將兩幅圖的SSIM定義為

式中C1,C2是穩定常數。為了避免分母為0造成系統的不穩定，令C1=(k1L)2,C2=(k2L)2,k1?1,k2?1 ,k1,k2為值很小的常數，L為圖像灰度級數，對于8 bit灰度圖像，L=255 。

3 基于小波稀疏的圖像處理

3.1 實驗裝置

無透鏡全息顯微鏡如圖4所示。一種局部相干光源（氙燈附在單色器上，帶寬5 nm），耦合到單模光纖（直徑100 μm）。取樣距離（光源到樣本的距離）Z1為10 cm，傳感器距離（樣本到傳感器的距離）Z2為0.7～1 mm。使用CCD傳感器對樣品進行采樣，此時，樣品的視場等于CCD的有效區域，這樣得到無透鏡全息圖，通過對不同Z2上的樣品進行多重強度測量來重建密集樣本的圖像。考慮到在線全息圖可能出現的旋轉和變化，需要對成像數據進行數字注冊、對準，然后經過迭代處理，恢復缺失的光學信息，這樣就可以在不需要任何復雜的光學系統的情況下，實現樣本的顯微成像[16]。

圖4 全息顯微鏡工作圖Fig.4 Hologram microscopy

3.2 實驗結果

為了驗證基于小波稀疏的圖像重建算法，在不同的高度（即樣品到傳感器的距離）獲得了一組（8幅）圖。首先，將基于迭代的多高度恢復方法應用于這8幅全息圖上，并將此恢復的高分辨圖作為參考圖像，如圖5所示。用基于小波稀疏的方法來恢復同樣的3幅不同高度的圖像，效果是可以與8幅圖的恢復結果相對比的，如圖6所示。為了量化圖像重建的質量，我們對這些圖像進行SSIM計算，結果如表1所示。對于人體血液樣本，用基于小波稀疏的重建方法，其SSIM值為0.840 7；在此基礎上，用4幅不同高度的全息圖進行小波稀疏恢復，結果如圖7所示，其SSIM值為0.870 3。

圖5 8幅圖迭代重建結果Fig.5 Iterative reconstruction results of eight images

圖6 3幅圖小波稀疏重建結果Fig.6 Iterative reconstruction results of three images

表1 不同切片對應恢復方法的SSIM值Tab.1 The SSIM value of different slices corresponds to the recovery method

圖7 4幅圖小波稀疏重建結果Fig.7 Iterative reconstruction results of four images

以上結果表明，我們可以減少至少兩倍的全息圖數量將圖像恢復出來，這不僅減少了測量的次數和時間，同時還能滿足空間分辨率以及顯微鏡的視野，這對于無透鏡顯微鏡的實現及其重要。在基于稀疏的多高度恢復方法中，我們使用了一個CCD傳感器，它的像素大小為 2.2 μm，達到了傳統臺式顯微鏡的分辨率。這不僅不需要顯微鏡復雜的設計結構，也不需要很多的鏡片來成像，還降低了顯微鏡的成本。

我們已經證明了多高度全息成像可以用稀疏表示來恢復圖像，但同時，基于稀疏的信號恢復還可以用于其它的物理測量，例如，多角度照明，波長掃描等，這些在生物樣品的測量方面運用非常廣泛。

另外，本文所述的小波變換可以是很多種小波變換，例如μmCDF97小波變化，這在壓縮圖像方面也有很大的運用。對于稀疏表示，還可以運用自適應的方法，例如字典學習都可以達到稀疏化，超分辨的目的。對于本項工作而言，其主要目的是減少原始數據的測量，同時保證圖像的質量，因此，選擇合適的測量方法以達到所要求的目標是最重要的。

重構算法中一個很重要的方面就是初始化，當在自由空間傳播時，低空間頻率的信號包含了關于樣本的大部分信息，因此低頻小波帶是不能被認為是稀疏的。另一方面是各個全息圖的距離需要經過不斷的嘗試，找到初始化最優時的距離。

4 結 論

本文研究了一種基于小波稀疏的圖像重建算法，用于對密集連接的樣本進行數字在線全息成像。這種算法能夠利用不同的高度（樣品到傳感器距離）的少量全息圖來重構生物樣本的圖像，這比之前基于迭代的多高度重建方法中使用的全息圖的數量至少減少了兩倍。使用人體血液切片實現了無透鏡超分辨的要求，且視野達到了20 mm2，這對于生物醫學、臨床醫學等方面都會有很大的幫助，大大提高了實驗效率，同時還降低了顯微鏡的成本。這種基于稀疏的重建方法還可以運用在其他超分辨全息成像技術中，例如，多個照明角度或多個照明波長，這些成像技術都可以用來增強相干全息顯微鏡的空間帶寬。