形式三角矩陣半環上的雙導子

陳艷平， 莊金洪， 譚宜家

(1. 福建商學院信息工程學院， 福建 福州 350012； 2. 福州大學數學與計算機科學學院， 福建 福州 350108)

0 引言

作為模糊代數的推廣， 半環理論已在數學的多個領域以及計算機科學、 系統理論分析與信號處理、 自動機理論、 開關理論與控制論、 優化理論等其他學科中有著廣泛的應用， 這些學科領域中的許多問題可轉化為某類半環上的相關問題[1-2]. 半環上的導子是半環理論中重要研究內容之一[3-5], 應用廣泛[1-2, 6-7]. 文獻[3]討論了交換半環上的上三角矩陣代數的 Jordan 導子； 文獻[4]研究了半環上某些特殊類型的矩陣半環的導子; 文獻[5]討論了多項式半環的導子.

形式矩陣環是一類非常重要的非交換環， 在有限維代數和算子代數研究中較常見， 是環和模中非對稱性質的構造例子和重要反例來源， 也是近期矩陣研究中較活躍的方向之一. 文獻[8]證明了非交換素環上的形式三角矩陣環的雙導子必是內導子， 推廣了文獻[9]的結論; 文獻[10]又將此結論推廣到幺環上的形式三角矩陣代數上; 文獻[11]得到了三角代數上滿足廣義恒等式的導子的結構.

1.2.1.2 患者方面:攜帶物品較多;文化層次普遍偏低,習慣物品亂堆放;對醫院規章制度和病房管理了解甚少,部分病人認為與自己無關。

三角矩陣半環、 形式三角矩陣環都是特殊的形式三角矩陣半環. 本文在上述基礎上進一步研究形式三角矩陣半環上的雙導子， 探討加法可消交換半環上形式三角矩陣半環的雙導子的基本性質， 及其與兩個半環的雙導子及雙半模同態之間的關系， 從而獲得三角矩陣半環雙導子的等價刻畫.

1 預備知識

定義1[1]設R是一個非空集合， “+”與“·”是R的兩個代數運算. 如果以下條件滿足:

a) (R, +, 0) 是一個交換幺半群， 其中 0 為R的加法恒等元；

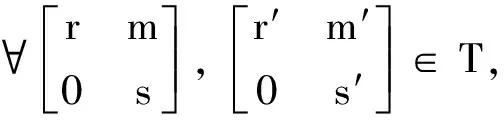
很多中小企業受到傳統管理理念的影響，尚未構建科學完善的管理模式，在實際工作中仍然采用傳統家族式的管理方法，因此造成對企業財務工作負責的工作人員多數是企業領導者的親屬，專業能力不強，無法結合市場動態變化對財務報告進行完善，也難以針對財務會計工作實施科學化的管理，導致在中小企業的建設和發展過程中，不能發揮出財務會計管理工作的效能，不僅會影響中小企業發展過程中經濟效益的獲取，甚至會制約和阻礙中小企業在當前市場經濟背景下實現持續穩定發展的目標。

c )對任意的a,b,c∈R， 均有a·(b+c)=a·b+a·c， (b+c)·a=b·a+c·a；

d) 對任意的a∈R, 0·a=a·0=0成立；

e) 0≠1.

則稱R為一個半環， 記為(R, +, ·, 0, 1) 或簡記為R.通常，a·b簡記為ab.

一個半環R稱為交換的， 如果?a,b∈R， 均有ab=ba.一個半環R稱為非負的， 如果?a,b∈R由a+b=0 可推出a=b=0.非負半環又稱為反環或零和自由半環[1].顯然， 任何帶有單位元的環都是半環， 每一個布爾代數(包括二元布爾代數)、 模糊代數、 每一個有界分配格以及任何坡都是非負交換半環.另外， 非負實數集對于數的加法與乘法也構成一個非負交換半環.

一個半環R稱為加法可消的， 如果?a,b,c∈R, 由a+c=b+c可推出a=b.半環R中的元素a稱為可反的， 如果存在b∈R， 使得a+b=0， 記b=-a， 稱b為a的反元.?c∈R, 定義c-a=c+(-a).易證， 若a是可反元， 則?c∈R,ac與ca均是可反元且-(ac)=(-a)c， -(ca)=c(-a).若R中所有可反元的全體記作V(R)， 則V(R)非空且是R的一個理想.

定義2[1]半環R上的一個左半模(簡稱左R-半模)是一個交換幺半群(M, +, 0)， 并且存在一個映射R×M→M， (r,m)→rm， 滿足對于任意r,r′∈R,m,m′∈M， 均有：

Ⅰ)r(m+m′)=rm+rm′； Ⅱ) (r+r′)m=rm+r′m；

Ⅲ) (rr′)m=r(r′m)； Ⅳ) 1Rm=m；

(2)網絡貸款的現狀。根據艾瑞咨詢數據統計，2015年我國網絡貸款行業的交易金額達到8000億元，通過網絡取得貸款的用戶規模達到3970.1萬人。在交易結構中，非消費類網絡貸款大于消費類網絡貸款。

Ⅴ)r0=0=0m.

類似地， 可定義半環S的右S-半模.一個交換半群(M, +, 0)如果既是左R-半模又是右S-半模， 則稱其為(R,S)-雙半模， 且滿足?r∈R，m∈M，s∈S均有(rm)s=r(ms).在沒有特殊指明的情況下，R-半模是指左R-半模.左R-半模(右S-半模)稱為忠實的， 如果?r∈R(?s∈S)， 當?m∈M， 均有rm=0(均有ms=0)時，r=0(s=0).(R,S)-雙半模M稱為忠實的， 如果M既是忠實的左R-半模又是忠實的右S-半模.用V(M)表示半模M中所有可反元的全體， 易證， 若m∈V(M)， 則?r∈R,s∈S， 均有rm,ms∈V(M)且-(rm)=r(-m)， -(ms)=(-m)s.

定義3設R是一個半環，d：R→R是一個映射且滿足對于任意的x,y∈R, 均有d(x+y)=d(x)+d(y).d稱為R上的一個導子[1]， 如果d(xy)=d(x)y+xd(y).

定義4設R是半環，d：R×R→R是一個映射且對于任意的x,y,z∈R, 均有d(x+y，z)=d(x,z)+d(y,z),d(x，y+z)=d(x,y)+d(x,z).d稱為R上的雙導子[9]， 如果d(xy，z)=d(x,z)y+xd(y,z)，d(x，yz)=yd(x,z)+d(x,y)z.

3.2 普通高校的師資力量有待提高，專業的定向運動制圖人才需要大量培養，以滿足學生對定向運動的專業人才需求。

定義5[9]設R是一個半環，M是左R-半模， 映射f：M→M稱為左R-半模同態， 如果對于任意r∈R,m,m′∈M, 均有f(m+m′)=f(m)+f(m′),f(rm)=rf(m).類似可定義半環的右S-半模同態.設M是(R,S)-雙半模， 若映射f：M→M既是左R-半模同態又是右S-半模同態， 則稱f為(R,S)-雙半模同態.

為了進一步提高區縣級電視臺專題節目的質量，在節目拍攝手段上要下功夫、創新拍攝手段，這樣才能夠讓更多的觀眾產生新的興趣點。中央電視臺的新聞因具有權威性，所以專題節目用詞精準，所表達的意思言簡意賅。而區縣級的觀眾從一定程度上來說，觀眾的文化水平以及專業素質相對較低，在拍攝手段上盡可能以簡單直觀的方式進行拍攝，這樣便于地方觀眾理解，容易引起觀眾的共鳴，一定程度上拉近節目與群眾之間的距離，吸引觀眾關注自己的節目。以普法為例，在劇本上以及人物講述角度上，可以采取第一人稱的拍攝手法，語言通俗易懂，鏡頭簡單明了，這樣觀眾就更容易理解和掌握法律知識。

設M是(R,S)-雙半模.映射f：M×M→M稱為(R,S)-雙半模雙同態， 如果對于任意的r,r′∈R,s,s′∈S,m,m1,m′∈M, 均有f(m+m1,m′)=f(m,m′)+f(m1,m′),f(m,m1+m′)=f(m,m1)+f(m,m′),f(rms,m′)=rf(m,m′)s,f(m,r′m′s′)=r′f(m,m′)s′.

四是優化綜合利用。積極探索政府、合作社、農戶3方利益聯結機制，大力推廣“秸稈全量深翻還田”“秸稈全覆蓋免耕還田”“水田秸稈全量還田”“秸稈能源生態”等典型利用模式，因地制宜開展“五化”利用。加大秸稈收購點設置，縮短農戶與企業之間的“距離”，減少秸稈田間源頭數量。例如，沅江市南嘴鎮在7個村設置回收點，安排專人負責收購，效果良好。

定義6[12]設R,S是兩個半環，M是一個非零的(R,S)-雙半模， 令

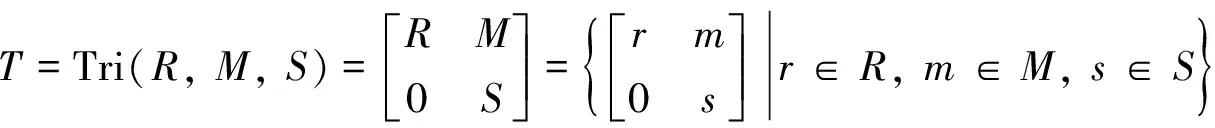
在當前社會中，為了能夠促進鄉村生態旅游在互聯網+背景下得到更好的發展，那么當地的負責部門就可以充分發揮出培訓機構的作用，選擇合適的培訓機構來為鄉村生態旅游經營者們提高職業技能培訓，并提供相應的平臺來讓他們互相交流和學習。與此同時，當地政府也可以積極地引進懂得生態旅游經營知識和電子商務的復合型人才，對鄉村生態旅游經營者們定期進行網絡信息化培訓和現場指導，使他們都能夠掌握相關的技能。

不難證明，T是一個半環, 稱之為形式三角矩陣半環， 也稱為半環上的廣義三角矩陣半環.若無特別說明， 本研究中T均表示加法可消的形式三角矩陣半環.

2 主要結論

引理1設T=Tri(R,M,S)，d：T×T→T是雙導子.則對于任意X,Y,U,V∈T， 均有：

1)p(m)∈V(M)， 并且d(rE11,mE12)=rp(m)E12,d(sE22,mE12)=-p(m)sE12,δ(r,r′)m+r′rp(m)=rr′p(m),mγ(s,s′)+p(m)s′s=p(m)ss′.

ⅱ)d(X,Y)VU+XYd(U,V)=d(X,Y)UV+YXd(U,V).

證明 ⅰ)d(0,X)=d(0·0,X)=0·d(0,X)+d(0,X)·0=0， 同理可證d(X,0)=0；d(I,X)=d(I·I,X)=I·d(I,X)+d(I,X)·I=d(I,X)+d(I,X)， 由半環T的加法可消性， 得d(I,X)=0， 同理可證d(X,I)=0.

ⅱ) 由于d(XU,YV)=Xd(U,YV)+d(X,YV)U=XYd(U,V)+Xd(U,Y)V+Yd(X,V)U+d(X,Y)VU， 同時,d(XU,YV)=Yd(XU,V)+d(XU,Y)V=YXd(U,V)+Yd(X,V)U+Xd(U,Y)V+d(X,Y)UV.于是，XYd(U,V)+Xd(U,Y)V+Yd(X,V)U+d(X,Y)VU=YXd(U,V)+Yd(X,V)U+Xd(U,Y)V+d(X,Y)UV， 由半環T的加法可消性可得:

d(X,Y)VU+XYd(U,V)=d(X,Y)UV+YXd(U,V)

(1)

證明 1) 設d(E11,mE12)=δ(m)E11+p(m)E12+γ(m)E22.利用d(E11,mE12)=d(E112,mE12)=E11d(E11,mE12) +d(E11,mE12)E11及T的加法可消性， 可得:δ(m)=γ(m)=0.于是存在映射p：M→M， 使得:

證明 設d(X,Y)=rE11+mE12+sE22，r∈R,m∈M,s∈S.在式(1)中， 取U=E11,V=m1E12，m1∈M， 利用XY=YX及T的加法可消性， 可得: (rE11+mE12+sE22)(m1E12)=0， 于是,rm1E12=0， 那么,rm1=0.由M是非零忠實的左R-半模， 得r=0.利用式(1)有:d(E11,m2E12)YX+E11(m2E12)d(X,Y)=d(E11,m2E12)XY+(m2E12)E11d(X,Y).利用XY=YX及T的加法可消性， 可得: (m2E12)(rE11+mE12+sE22)=0， 于是,m2sE12=0， 那么,m2s=0.由M是非零忠實的右S-半模， 得:s=0.于是，d(X,Y)=mE12,m∈M.

引理3設T=Tri(R,M,S)， 且M是忠實的(R,S)-雙半模，d：T×T→T是一個雙導子.則存在m*∈V(M)、R上的雙導子δ和S上的雙導子γ， ?r,r′∈R，s,s′∈S， 均有:

a)rr′m*=r′rm*，m*ss′=m*s′s；

b)d(rE11,sE22)=d(sE22,rE11)=-rm*sE12；

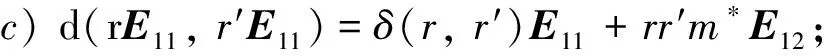
兵團城市的地域性設計策略研究——以十三師紅星市中心城區城市設計為例 彭雄亮 姜洪慶2018/01 09

證明 a) 由引理2知， 存在m*∈M， 使得:d(E11,E11)=m*E12.由引理1中 ⅰ)可知，d(E22,E22)+d(E11,E22)=0，d(E11,E22)+d(E11,E11)=0， 所以m*∈V(M).再由T的加法可消性知，d(E22,E22)=d(E11,E11)=m*E12.再利用引理1 中ⅰ)可得:d(E11,E22)=d(E22,E11)=-m*E12.

⑨ ? ? Caronline Rogus，“Fighting the Establishment:The Need for Procedural Reform of Our Paternity Laws”，Michigan Journal of Gender＆ Law，67(21)，2014，p．79，p．98，pp．114 ～115．

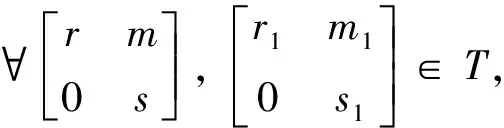
b) 由于(rE11)(E22)=(E22)(rE11)=0， 由引理2知， 存在m1∈M， 使得:d(rE11，E22)=m1E12.于是，d(rE11，E22)=d((rE11)E11，E22)=(rE11)d(E11，E22)+d(rE11，E22)E11=(rE11)(-m*E12)+(m1E12)E11=r(-m*E12)=-rm*E12.由于 (rE11)(sE22)=(sE22)(rE11)=0， 由引理2知， 存在m2∈M， 使得:d(rE11，sE22)=m2E12.于是,d(rE11，sE22)=d(rE11，E22(sE22))=E22(m2E12)+(-rm*E12)(sE22)=-rm*sE12.

同理可證，d(sE22,rE11)=-rm*sE12.

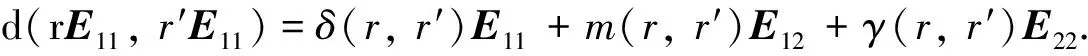
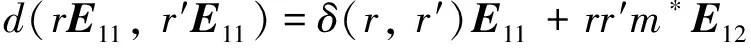
(2)

下證δ：R×R→R是R上的雙導子.

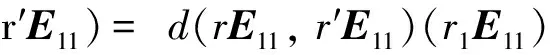
d) 類似于c)可證.

引理4設T=Tri(R,M,S)， 且M是忠實的(R,S)-雙半模，d：T×T→T是雙導子.則存在(R,S)-雙半模同態p：M→M和q：M→M， ?r,r′∈R,s,s′∈S,m∈M， 均有:

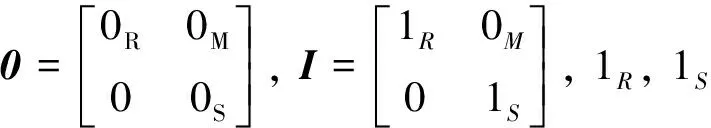
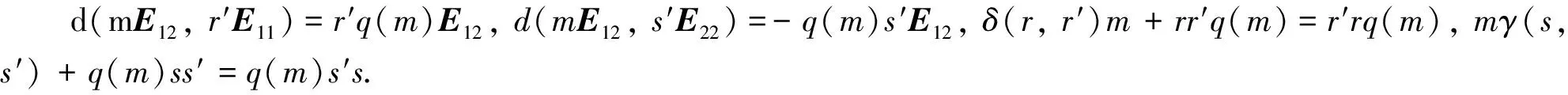
引理2設T=Tri(R,M,S)， 且M是忠實的(R,S)-雙半模，d：T×T→T是雙導子.若X,Y∈T滿足XY=YX， 則存在m∈M， 使得d(X,Y)=mE12.

d(E11,mE12)=p(m)E12

(3)

由引理1中 ⅰ)知,p(m)∈V(M)， 且d(E22,mE12)=-p(m)E12.現設d(rE11,mE12)=δ(r,m)E11+p(r,m)E12+γ(r,m)E22.由rE11=(rE11)E11及式(3)， 可得:d(rE11,mE12)=(rE11)d(E11,mE12)+d(rE11,mE12)E11=rp(m)E12+δ(r,m)E11.又由mE12=(mE12)E22及引理3 中b)， 可得 :

本課程主要采取項目教學的方法和一體化教學的方式。以任務驅動、項目引領型課程為主體結構，按照實際工作任務、工作過程和工作情境來組織課程。從崗位需求出發，盡早讓學生進入工作實踐。以工作任務為中心來整合相應的知識和技能，實現理論與實踐的統一，為學生提供體驗完整工作過程的學習機會，從而改變以前電工電子的系統教學框架，使知識結構、技能要求、教學內容彈性化。教學過程主要在實驗實訓室完成，讓學生邊學邊做，在學中做、做中學，將動手動腦緊密結合，相得益彰，即完成了一體化教學。

d(rE11,mE12)=d(rE11,mE12)E22+(mE12)d(rE11,E22)=rp(m)E12

(4)

類似可證d(sE22,mE12)=-p(m)sE12.下證， 映射p：M→M是(R,S)-雙半模同態.

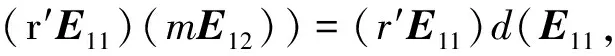
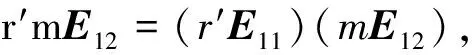
類似可證，ξ(m,m′)ss′=ξ(m,m′)s′s.

克氏綜合征又稱曲細精管發育不全癥，其基本臨床特征為：不同程度男性性成熟障礙、小睪丸、無精子癥、青春期明顯乳房發育、高促性腺激素水平[3]。生殖細胞減數分裂過程中染色體不分離導致性染色體二體生殖子產生，是本病的遺傳病理機制[4]。此病在嬰幼兒期不易發現異常，青春發育期睪丸小才被發現，出現某些女性體征才會引起注意，但大部分患者因婚后不育到醫院就診才能確診。絕大多數的患者射出的外周精液中是沒有精子的，但極個別報道精液中偶見精子[5]。本例患者不但精液中有精子，而且妻子自然受孕生育1胎，實為罕見。其原因可能是其中一條X染色體處于失活狀態，但具體機制有待進一步研究。

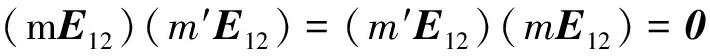
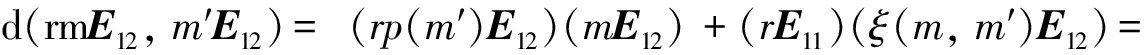
2)類似于1)可證.

b) (R, ·, 1) 是一個幺半群， 其中 1 為R的乘法恒等元；

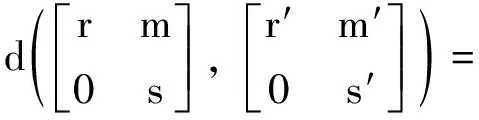
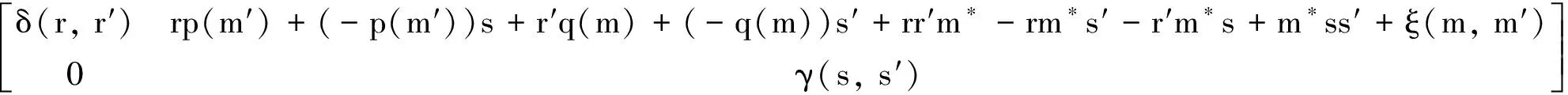
① 對于任意m∈M,p(m),q(m)∈V(M)；

② ?r,r′∈R,s,s′∈S,m,m′∈M， 均有：

δ(r,r′)m′+r′rp(m′)=rr′p(m′),m′γ(s,s′)+p(m′)s′s=p(m′)ss′

δ(r,r′)m+rr′q(m)=r′rq(m),mγ(s,s′)+q(m)ss′=q(m)s′s
rr′ξ(m,m′)=r′rξ(m,m′),ξ(m,m′)ss′=ξ(m,m′)s′s.

證明 充分性： 通過直接計算可知d是T的雙導子.下證必要性.

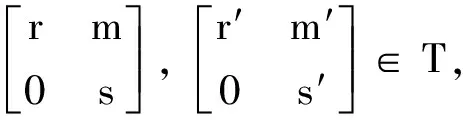
由引理4～5， 可得①～②. 證畢.

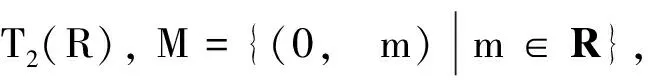
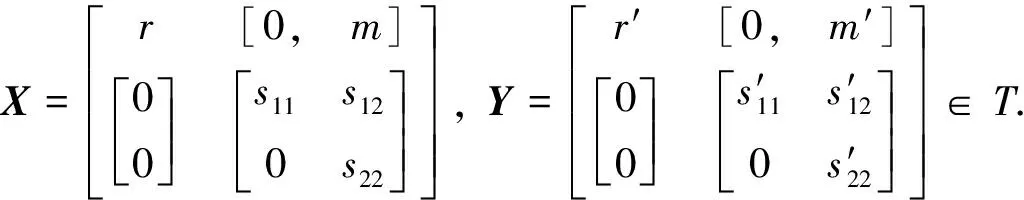
SF用它的經營理念更快幫助客戶、對市場更快更好地做出反應：為了提高企業的市場競爭力不斷地推出新產品，使服務周期能夠縮短；調整競爭策略，使經營成本能夠降低。SF為國民經濟的持續健康發展貢獻了稅收做出了積極貢獻，它的企業規模也在緩解社會就業壓力上做出了應有的積極貢獻。

經計算， 可知d：T×T→T是雙導子.

經超聲檢查后，本組60例患者均明確診斷，診斷符合率100%，其中慢性闌尾炎急性發作7例、闌尾周圍膿腫6例、急性化膿性闌尾炎14例、急性單純性闌尾炎26例，急性壞疽穿孔性闌尾炎7例、。其中闌尾腔有糞石者11例。見表。

3 結論

本研究分析了形式三角矩陣半環雙導子. 探討了加法可消交換半環上形式三角矩陣半環Tri(R,M,S)的雙導子的基本性質及判定方法， 給出了形式三角矩陣半環 Tri(R,M,S)的雙導子與兩個半環R與S的雙導子及(R,S)-雙半模同態之間的關系， 從而獲得了三角矩陣半環雙導子的等價刻畫.