地下道路結構中反應位移法計算參數影響分析

顧志超

（上海市政交通設計研究院有限公司，上海市200030）

0 引言

隨著經濟和社會的發展，城市人口日趨集中，交通擁堵問題日益嚴重，修建地下道路也成為各大城市改善交通環境的一個發展趨勢[1]。

我國位于世界兩大地震帶――環太平洋地震帶與歐亞地震帶之間，受太平洋板塊、印度板塊和菲律賓海板塊的擠壓，地震斷裂帶十分活躍。1995年日本阪神地震和2008年中國汶川地震都表明，地下結構在地震作用下并不是絕對安全的，應加強地下結構抗震設計[2-3]。

目前地下結構抗震分析理論主要分為解析法、數值法和簡化實用分析方法。其中，簡化分析方法由于具有概念明確、計算簡單、精度相對較高等特點，在實際工程設計中得到了廣泛應用[4]。GB/T 51336—2018《地下結構抗震設計標準》中明確推薦地下道路結構采用反應位移法進行抗震分析。

反應位移法取地震時地下結構周邊地層的變形作為地震作用，該方法概念清晰，比較符合地下結構的地震振動特性。劉晶波等[5-7]指出經典反應位移法是一種較為實用的地下結構地震反應分析方法，反應位移法的計算結果易受計算參數的影響，在各計算參數中，地層剪應力對結構內力計算結果影響最大，地層變形其次，然后是慣性力，彈簧系數的影響最小。

本文在已有研究的基礎上，針對地下道路結構中反應位移法各計算參數對計算結果的影響進行相關探討，以期找出地震情況下地下道路結構最不利斷面所處位置，為實際工程設計提供參考。

1 反應位移法基本原理

根據GB 50909—2014《城市軌道交通結構抗震設計規范》相關規定，采用反應位移法進行抗震分析時，主要需要計算土層位移、結構慣性力、土層剪力，并確定地基彈簧，見圖1。

圖1 計算模型簡圖

1.1 土層位移

土層位移假設為余弦函數，具體公式如下：

式中：umzx為場地地表最大位移，可根據地震動峰值加速度按規范取值；z為計算點埋深，h為設計地震作用基準面的深度。由此可見，對于某一特定地區的地下道路結構而言，影響土層位移的主要參數為結構覆土厚度h1和基準面深度h。

1.2 結構慣性力

對于某一特定地區的地下道路結構而言，結構慣性力只與結構質量有關。

1.3 土層剪力

對土層位移微分求出土層應變，再通過物理關系可確定土層剪力：

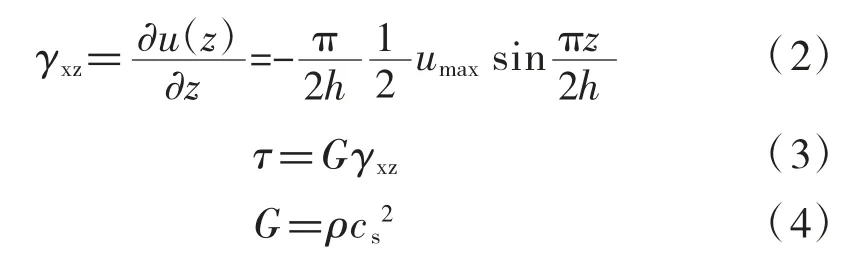
式中：ρ為土的質量密度；cs為土體的剪切波速。由此可見，對于某一特定地區的地下道路結構而言，影響土層剪力的主要參數為結構覆土厚度h1、基準面深度h和土體剪切波速cs。

1.4 地基彈簧

地基彈簧不是一個獨立的土體特性，他的取值與土體性質、基礎尺寸等均有關系[8]。目前，地基彈簧的取值方法主要有試驗法、有限元法和經驗公式法。試驗法和有限元法可以較為準確的得出地基彈簧系數，但是無法反映出地基彈簧與土體性質、基礎尺寸的具體關系。為更加準確的研究各計算參數對反應位移法結果的影響，本文采用李英民法[9]來確定地基彈簧系數。李英民法地基彈簧經驗公式可表示為：

結構底板法向和切向彈簧：

結構側墻法向和切向彈簧：

式中：B為結構橫截面寬度；H為結構橫截面高度（對于單層地下道路結構而言，H變化不大，可取為常數）；h2為結構底板至基準面的土層厚度；a1、a2、b1、b2為系數。土體泊松比ν一般在0.25~0.4之間，ν的取值對地基彈簧系數取值的影響只有12%，對結構性狀變化影響更小[10]。為便于分析，ν統一取為0.25。由此可見，對于某一特定地區的單層地下道路結構而言，影響地基彈簧的主要參數為結構覆土厚度h1、基準面深度h、土體剪切波速cs和結構橫斷面寬度B。綜上所述，對于某一特定地區的單層地下道路結構而言，影響反應位移法計算結果的主要參數為結構覆土厚度h1、基準面深度h、土體剪切波速cs和結構橫斷面寬度B。

2 模型建立

西安地區某地下道路工程雙向四車道標準斷面見圖2，結構橫斷面寬度B=21.1 m，結構高度H=8.1 m，結構覆土厚度h1=3 m，土體剪切波速cs=250 m/s，基準面深度h=70 m。場地抗震設防烈度為8度，設計基本地震加速度為0.20g，所屬設計地震分組為第二組，場地類別為Ⅱ類。

圖2 地下道路結構橫斷面圖

采用Autodesk Robot Structural Analysis Professional結構有限元計算軟件建立上文所述基本模型，并分別單獨變化結構覆土厚度h1、基準面深度h、土體剪切波速cs和結構橫斷面寬度B這四個參數，其中結構覆土厚度h1取1.5 m、3 m、4.5 m、6 m、7.5 m，基準面深度h取30 m、40 m、50 m、60 m、70 m，土體剪切波速cs取100 m/s、150 m/s、200 m/s、250 m/s、300 m/s，結構橫斷面寬度B取14.1m（雙向二車道）、21.1 m（雙向四車道）、28.1 m（雙向六車道）、35.1 m（雙向八車道）、42.1 m（雙向十車道）。以此觀察每個參數的變化對結構地震作用結果的影響。

3 反應位移法計算參數影響分析

由于在承載能力極限工況下地下道路結構內力也會隨著結構覆土厚度h1、基準面深度h（影響地基彈簧）、土體剪切波速cs（影響地基彈簧）和結構橫斷面寬度B這四個參數的變化而變化，為了更加準確地反映出上述四個參數對地震作用結果的影響，選取結構內力放大系數η（地震作用工況下結構內力與承載能力極限工況下結構內力的比值）作為參數影響分析的指標。根據地下道路結構斷面形式，分別選取頂板-彎矩（T-M）、底板彎矩（B-M）、側墻-彎矩（S-M）、頂板-剪力（T-S）、底板-剪力（B-S）、側墻-剪力（S-S）、頂板-軸力（T-A）、底板-軸力（B-A）、側墻-軸力（S-A）、中墻-軸力（M-A）進行分析。

3.1 結構覆土厚度的影響

以基本模型為基礎，結構覆土厚度h1分別取1.5 m、3 m、4.5 m、6 m、7.5 m，建立5個模型，并采用反應位移法計算各模型的結構內力放大系數η。為便于比較，對結構內力放大系數η以基本模型h1=3 m為基準作歸一化處理，可得結構覆土厚度變化對結構內力放大系數的影響趨勢，見圖3。

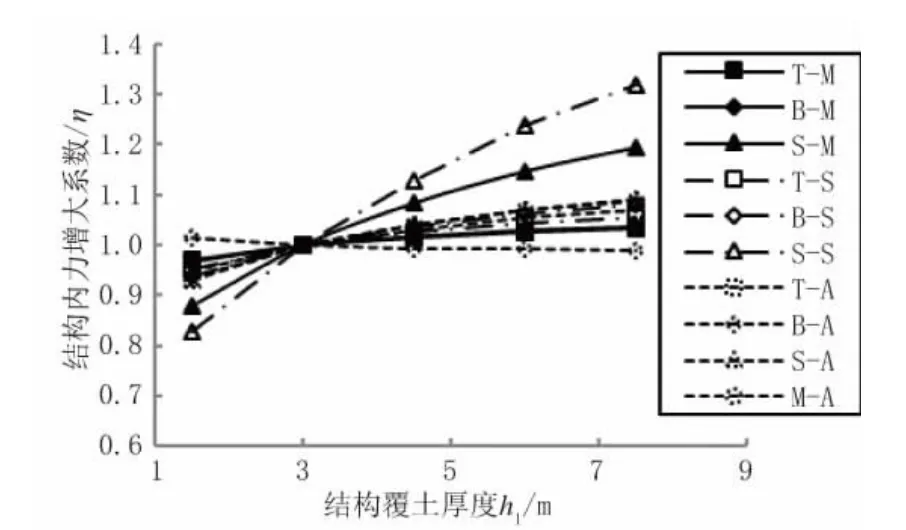
圖3 結構內力放大系數與結構覆土厚度關系圖

由圖3可以看出，隨著結構覆土厚度的增大，結構各部位內力放大系數增大，其中側墻剪力的放大系數變化最大，覆土厚度h1=7.5 m的模型結構側墻剪力放大系數約為覆土厚度h1=3 m的1.32倍。

3.2 基準面深度的影響

以基本模型為基礎，基準面深度h分別取30 m、40 m、50 m、60 m、70 m，建立5個模型，并采用反應位移法計算各模型的結構內力放大系數η。對結構內力放大系數η以基本模型h=70 m為基準作歸一化處理，可得基準面深度變化對結構內力放大系數的影響趨勢，見圖4。

圖4 結構內力放大系數與基準面深度關系圖

由圖4可以看出，隨著基準面深度的增大，結構各部位內力放大系數減小，其中底板軸力的放大系數變化最大，基準面深度h=30 m的模型結構底板軸力放大系數約為基準面深度h=70 m的4.47倍。

3.3 土體剪切波速的影響

以基本模型為基礎，土體剪切波速cs分別取100 m/s、150 m/s、200 m/s、250 m/s、300 m/s，建立5個模型，并采用反應位移法計算各模型的結構內力放大系數η。對結構內力放大系數η以基本模型cs=250 m/s為基準作歸一化處理，可得土體剪切波速變化對結構內力放大系數的影響趨勢，見圖5。

由圖5可以看出，隨著土體剪切波速的增大，結構各部位內力放大系數增大，其中底板軸力的放大系數變化最大，土體剪切波速cs=250 m/s的模型結構底板軸力放大系數約為土體剪切波速cs=100 m/s的2.22倍。

圖5 結構內力放大系數與土體剪切波速關系圖

3.4 結構橫斷面寬度的影響

以基本模型為基礎，結構橫斷面寬度B分別取14.1 m、21.1 m、28.1 m、35.1 m、42.1 m，建立5個模型，并采用反應位移法計算各模型的結構內力放大系數η。對結構內力放大系數η以基本模型B=21.1 m為基準作歸一化處理，可得結構橫斷面寬度變化對結構內力放大系數的影響趨勢，見圖6。

圖6 結構內力放大系數與結構橫斷面寬度關系圖

由圖6可以看出，隨著結構橫斷面寬度的增大，結構各部位彎矩放大系數減小、側墻剪力放大系數增大、頂板及底板軸力放大系數增大、側墻軸力放大系數減小，其中側墻剪力的放大系數變化最大，結構橫斷面寬度B=42.1 m的模型結構側墻剪力放大系數約為結構橫斷面寬度B=21.1 m的2.31倍。

4 結論

本文在已有研究的基礎上，針對地下道路結構中反應位移法各計算參數對結構內力變化的影響進行相關探討，得出以下主要結論：

（1）地震作用下，隨著結構覆土厚度的增大，結構各部位內力放大系數增大。

（2）地震作用下，隨著基準面深度的增大，結構各部位內力放大系數減小。

（3）地震作用下，隨著土體剪切波速的增大，結構各部位內力放大系數增大。

（4）地震作用下，隨著結構橫斷面寬度的增大，結構各部位彎矩放大系數減小、側墻剪力放大系數增大、頂板及底板軸力放大系數增大、側墻軸力放大系數減小。

根據上述結論，對于某一特定地區的單層地下道路結構而言，可以快速判斷出在地震作用下結構最不利位置處于結構覆土厚度最大、基準面深度最小、土體剪切波速最大處。結構橫斷面寬度對結構各內力的影響不盡相同，需具體分析。