重力式錨碇抗滑移穩(wěn)定性設(shè)計參數(shù)敏感性分析

曹茜

［同濟大學(xué)建筑設(shè)計研究院（集團）有限公司，上海市200092］

0 引 言

隨著我國大跨徑懸索橋修建數(shù)量的不斷增加和技術(shù)水平的提高，橋梁結(jié)構(gòu)設(shè)計已經(jīng)逐漸輕盈化、纖細(xì)化，在保證結(jié)構(gòu)受力安全和穩(wěn)定的前提下，盡量減小結(jié)構(gòu)尺寸和降低造價的需求日益增加。然而，大跨徑懸索橋關(guān)鍵構(gòu)件的設(shè)計分析理論研究相對滯后，限制了大跨徑懸索橋的經(jīng)濟性。重力式錨碇是懸索橋中常采用的錨固系統(tǒng)之一，其穩(wěn)定性對結(jié)構(gòu)安全運營至關(guān)重要，也是懸索橋精細(xì)化設(shè)計理論中亟需解決的關(guān)鍵問題。

對大跨度懸索橋錨碇的穩(wěn)定性分析得到了眾多研究人員的關(guān)注，例如劉家峽黃河特大橋的重力錨結(jié)構(gòu)受力穩(wěn)定性與監(jiān)控研究[1]、潤揚大橋北錨碇的抗滑動和抗滑移穩(wěn)定性研究[2]、虎門大橋東錨碇穩(wěn)定性分析和評價[3]、矮寨大橋的錨碇穩(wěn)定和應(yīng)力分析[4]、泰州大橋錨碇穩(wěn)定性和變形分析[5]。通過對影響錨固系統(tǒng)各參數(shù)的分析，孫華安[6]識別出主纜纜力大小、主纜纜力轉(zhuǎn)角、散索鞍與前錨面的距離以及前后錨面之間的距離是影響錨固系統(tǒng)安全性和決定錨碇尺寸的關(guān)鍵設(shè)計參數(shù)。蘇靜波等[2]采用有限元軟件，分析了錨碇基礎(chǔ)前后墻土體壓力對其穩(wěn)定性的影響，發(fā)現(xiàn)后墻土壓力對錨碇穩(wěn)定性的影響略大于前墻土壓力的影響，此外摩擦系數(shù)是至關(guān)重要的影響參數(shù)。

重力式錨碇作為大跨徑懸索橋中的關(guān)鍵構(gòu)件，是懸索橋設(shè)計經(jīng)濟性指標(biāo)的關(guān)鍵影響因素。本研究以一大型重力式錨碇為對象，對影響其優(yōu)化的設(shè)計參數(shù)進行敏感性分析，以識別出其中的關(guān)鍵因素，為優(yōu)化設(shè)計提供基礎(chǔ)。

1 工程概況

本研究以某一跨徑為1 490 m的懸索橋為背景，采用鋼結(jié)構(gòu)包括鋼箱梁為主梁、鋼混組合結(jié)構(gòu)橋塔和高強鋼絲主梁。該橋重力式錨碇采用69 m×50 m的矩形基礎(chǔ)，基坑開挖深度約48 m，地下連續(xù)墻圍護。依據(jù)地勘資料，錨碇基礎(chǔ)覆蓋層自上而下為填土、粉質(zhì)黏土、淤泥質(zhì)粉質(zhì)黏土、淤泥質(zhì)黏土、黏土、粉質(zhì)黏土、粉質(zhì)黏土夾黏質(zhì)粉土、砂質(zhì)粉土，在基坑開挖之前對基坑進行了降水處理。

2 計算模型

2.1 有限元模型建立及網(wǎng)格劃分

為計算恒載和活載共同作用下的主纜拉力，首先采用ANSYS建立全橋模型（見圖1），包括采用梁單元beam44模擬橋塔與加勁梁，材料采用Q345鋼；桿單元link10模擬主纜及吊桿單元，其中主纜材料為1 860 MPa高強鋼絲，吊桿是1 770 MPa高強鋼絲。據(jù)此建立的有限元模型包含主梁和索塔單元共計276個單元，主纜和吊桿共計902個單元。依據(jù)設(shè)計，全橋二期恒載取9 t/m，活載按照公路-I級車道荷載加載，橫向8車道，橫向折減系數(shù)取0.5，沖擊系數(shù)取1.3。

圖1 全橋有限元模型

其次采用Solid45單元模擬錨碇及基礎(chǔ)實體。在建模過程中不考慮地下連續(xù)墻復(fù)合基礎(chǔ)受力，將錨碇及基礎(chǔ)視為共同受力的整體結(jié)構(gòu)，建模范圍至封底混凝土底面位置(-48 m)。錨碇模型共有節(jié)點55 992個、實體單元135 540個，錨碇模型簡圖見圖2。依據(jù)設(shè)計，基礎(chǔ)及以下受到地下水浮力影響，豎向反力在計算完成錨碇及基礎(chǔ)整體重力后，按照基礎(chǔ)體積扣除相應(yīng)浮力。

圖2 錨碇模型簡圖

2.2 計算參數(shù)選取

本文所研究的懸索橋橋塔與加勁梁采用Q345鋼，主纜及吊桿分別采用1 860 MPa高強鋼絲和1 770 MPa鋼絲。錨碇由混凝土構(gòu)成，其中基礎(chǔ)和錨體混凝土為C30、錨碇前支墩混凝土為C40、填芯混凝土為C20。主橋各構(gòu)件所采用的材料屬性設(shè)計值見表1。

表1 材料屬性設(shè)計值

3 錨碇穩(wěn)定安全性驗算和敏感性分析

《公路懸索橋設(shè)計規(guī)范》（JTG/T D65-05—2015）規(guī)定，錨碇滑動安全系數(shù)取值平時大于2.0，地震時大于1.2。

3.1 抗滑動穩(wěn)定安全系數(shù)計算

利用前述建立的全橋有限元模型，考慮恒載與活載共同作用下的基本組合，計算得單根主纜纜力為6.77×108N，纜力方向根據(jù)主纜入射角與折射角間的關(guān)系確定。為分析錨碇在主纜纜力作用下的結(jié)構(gòu)響應(yīng)，根據(jù)主纜纜力作用方向分解后可知，其分別作用在前支墩（面壓力）和錨固面（面拉力）上。在主纜纜力作用下，錨碇產(chǎn)生水平方向的位移，同時在豎向纜力分量和自重共同作用下產(chǎn)生豎向位移。纜力的作用使得錨碇存在沿水平方向滑動的風(fēng)險，此外在豎向自重、基礎(chǔ)變位等共同作用下可能引起錨碇傾覆。

對控制重力式錨碇設(shè)計的抗滑移穩(wěn)定性進行驗算。首先，采用前述建立的錨碇有限元模型，分別考慮錨體混凝土、填芯混凝土、填芯水以及地下水等共同作用，并且將2根主纜纜力作用于錨碇上，計算得到錨碇的作用力；其次，從計算結(jié)果中提取出基礎(chǔ)底面豎向反力7.72×109N、水平力1.51×107N；最后，對錨碇抗滑動穩(wěn)定性進行驗算，驗算時考慮基礎(chǔ)底土層為黏性土，并根據(jù)工程經(jīng)驗將其與混凝土錨碇基底的摩擦系數(shù)取為0.4，再按照《公路懸索橋設(shè)計規(guī)范》中的抗滑穩(wěn)定性驗算公式，求得錨碇安全系數(shù)為2.049，大于上述規(guī)范規(guī)定的限值2.0，表明設(shè)計符合要求。

3.2 敏感性分析

敏感性分析假定結(jié)構(gòu)響應(yīng)Z（xi）中各設(shè)計參數(shù)在可能范圍內(nèi)進行變動，研究這些變動對最終輸出值的影響程度，影響程度的大小即為該屬性的敏感性系數(shù)。對于錨碇抗滑穩(wěn)定性的敏感性分析，可假定抗滑安全系數(shù)函數(shù)為Z（x）=K（x1，x2，…，xn），那么其中第i個參數(shù)的敏感度Si可表示為:Si=ΔZ/Δxi。其中ΔZ為極限狀態(tài)函數(shù)的變化；Δxi為第i個參數(shù)的變化。Si越大，在對應(yīng)條件下Z（xi）對xi越敏感。

3.2.1 纜力敏感性分析

錨碇抗滑移穩(wěn)定性受設(shè)計參數(shù)、材料屬性和幾何尺寸參數(shù)的影響，如基底摩擦系數(shù)、材料密度、纜力大小、施工導(dǎo)致的體積誤差等。經(jīng)過ANSYS計算，對主要參數(shù)進行5 000次超拉丁立方抽樣分析，其敏感性分析結(jié)果見圖3。圖3中條形圖表示1%的輸入?yún)?shù)變化引起的輸出參數(shù)百分比變化率；餅狀圖表示各變量敏感度在所有變量中所占比重。由圖3可見，主纜纜力主要受密度，尤其是用料較多的材料密度影響最大，對本文而言為主纜材料密度和加勁梁材料密度，其次受主纜材料彈性模量的影響，而主塔的材料參數(shù)影響不大。可見，為降低主纜纜力中的恒載成分，需考慮采用輕質(zhì)材料建造主纜和主梁，或進一步提高主梁材料強度以降低主纜和主梁材料用量。

圖3 纜力參數(shù)敏感性分析

3.2.2 錨碇抗滑動穩(wěn)定性敏感性分析

對材料密度、纜力大小進行了錨碇穩(wěn)定性的敏感性分析，結(jié)果見圖4。由圖4可知，錨碇抗滑移穩(wěn)定性受基底摩擦系數(shù)影響最大；與加勁梁密度、主纜密度呈負(fù)相關(guān)，與材料的密度呈正相關(guān)，且密度的敏感程度大小與材料實際用量直接相關(guān)，即主梁與主纜自重是主纜纜力的關(guān)鍵組成部分，增大主梁與主纜自重將導(dǎo)致錨碇滑動風(fēng)險增大。因此，對于重力式錨碇的抗滑安全性而言，首先應(yīng)當(dāng)保證基礎(chǔ)底面與地基之間有充足的摩擦，以抵抗主纜水平分力，對于水系發(fā)達的橋址，錨碇基底所處土層難以達到所需的摩擦系數(shù)，實際工程需采用相關(guān)地基處理方法對基礎(chǔ)底部土層進行改造以提供基底摩擦系數(shù)；其次可以通過增大錨體及填芯材料的用量以提高豎向力來增大抗滑力；最后可通過優(yōu)化結(jié)構(gòu)設(shè)計，降低由結(jié)構(gòu)自重引起的主纜纜力，從而降低其滑動力。

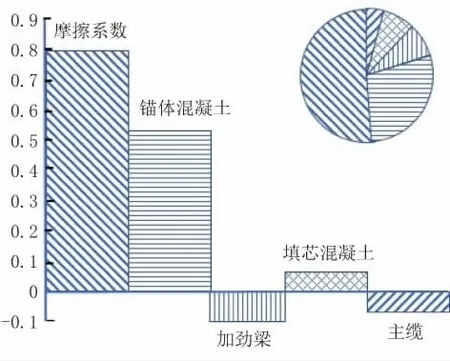
圖4 錨碇抗滑移能力的敏感性分析

4 結(jié)語

本文為探明錨碇設(shè)計中的關(guān)鍵控制參數(shù)，開展了錨碇抗滑動穩(wěn)定性設(shè)計參數(shù)的敏感性分析，分別識別出了主纜纜力和錨碇抗滑動中的關(guān)鍵設(shè)計參數(shù)，包括材料密度和基底摩擦系數(shù)等。其中主纜纜力受主纜材料、加勁梁材料的用量及其密度影響最大，即隨著懸索橋跨徑的增大，恒載產(chǎn)生效應(yīng)的是主纜纜力的顯著部分；錨碇穩(wěn)定性受基底摩擦系數(shù)影響最大，適當(dāng)進行基底摩擦系數(shù)的處理是提高錨碇抗滑動的重要手段之一。