固體火箭發(fā)動(dòng)機(jī)推進(jìn)劑/襯層/絕熱層粘接界面細(xì)觀損傷過程數(shù)值模擬研究 ①

伍 鵬，李高春，錢仁軍

(海軍航空大學(xué)，煙臺(tái) 264001)

0 引言

固體火箭發(fā)動(dòng)機(jī)的推進(jìn)劑/襯層/絕熱層粘接界面一直是薄弱環(huán)節(jié)，其粘接良好與否直接影響固體火箭發(fā)動(dòng)機(jī)的工作過程[1-2]。國內(nèi)外的研究表明，部分固體火箭發(fā)動(dòng)機(jī)的故障是由粘接界面失效而引發(fā)，因此對固體火箭發(fā)動(dòng)機(jī)粘接界面損傷過程一直是人們關(guān)注的重點(diǎn)。宏觀尺度下，例如對其進(jìn)行力學(xué)性能測試，或者采用界面單元對其進(jìn)行數(shù)值模擬等[3-5]，可為其力學(xué)性能評(píng)估提供參考，但無法揭示其細(xì)觀損傷機(jī)理。細(xì)觀尺度下，固體火箭發(fā)動(dòng)機(jī)的粘接界面包括推進(jìn)劑、襯層、絕熱層。由于推進(jìn)劑與襯層內(nèi)部顆粒夾雜的原因，細(xì)觀尺度粘接界面表現(xiàn)為各向異性材料，在外部載荷作用下，其損傷過程復(fù)雜。從細(xì)觀尺度對粘接界面進(jìn)行研究，能更好地解釋其失效機(jī)理。在試驗(yàn)方面，楊明等[6]采用掃描電鏡，對原位拉伸過程粘接界面的細(xì)觀形貌演化過程進(jìn)行了觀察，分析了顆粒脫濕尺寸與粘接界面失效過程之間的關(guān)系。伍鵬等[7]采用數(shù)字圖像相關(guān)方法，對細(xì)觀尺度下粘接界面的變形場進(jìn)行了測量，但由于測量手段的限制，沒有獲得粘接界面拉伸過程中的應(yīng)力等信息。因此，還需對界面失效過程開展數(shù)值模擬研究。在數(shù)值模擬方面，王廣等[8]通過微CT重構(gòu)的方式，建立了粘接界面的細(xì)觀結(jié)構(gòu)，模擬了老化條件下粘接界面的失效過程。李高春等[9]設(shè)計(jì)了微型粘接試件，建立了粘接界面的細(xì)觀模型，對其進(jìn)行了數(shù)值模擬。楊明與李高春的試驗(yàn)結(jié)果反映了粘接界面的兩種失效模式：界面脫粘與內(nèi)聚斷裂。尹華麗等[10-11]研究結(jié)果表明，初始粘接良好的粘接界面，其損傷形式主要為推進(jìn)劑一側(cè)內(nèi)部顆粒的脫濕與粘合劑基體的失效，即內(nèi)聚斷裂。針對推進(jìn)劑內(nèi)部的損傷過程，國內(nèi)外學(xué)者開展了大量研究[12-16]，但大部分文獻(xiàn)只是考慮推進(jìn)劑內(nèi)部顆粒的“脫濕”，實(shí)際上粘接界面的完整失效過程還應(yīng)包括推進(jìn)劑內(nèi)部粘合劑基體的損傷與失效。

為了更加完整地還原粘接界面的失效過程，本文通過建立粘接界面的細(xì)觀代表性體積單元，將基于表面粘結(jié)損傷的粘性接觸算法用于粘接界面推進(jìn)劑一側(cè)內(nèi)部顆粒脫濕的模擬，采用最大主應(yīng)力準(zhǔn)則用于模擬粘合劑基體的損傷與失效過程，為評(píng)估固體火箭發(fā)動(dòng)機(jī)粘接界面的力學(xué)性能提供參考。

1 粘接界面細(xì)觀損傷過程數(shù)值模擬

1.1 模型的建立

為方便描述，將某型固體火箭發(fā)動(dòng)機(jī)粘接界面簡稱為粘接界面。為了更好地對粘接界面的細(xì)觀損傷過程進(jìn)行數(shù)值模擬，需要建立粘接界面的代表性單元。細(xì)觀尺度下，粘接界面的代表性體積單元包括了HTPB推進(jìn)劑、HTPB/IPDI襯層、EPDM絕熱層。代表性體積單元的尺寸有兩方面的要求[16]：一方面要求其尺寸足夠大，能充分反映粘接界面的細(xì)觀形貌特點(diǎn)；另一方面為減小計(jì)算量，其尺寸又不能太大。對襯層的厚度進(jìn)行測量，將等間距的條件下襯層厚度測量值的平均值作為模型中襯層厚度，得到襯層厚度約為240 μm。由于本文采用的絕熱層模量遠(yuǎn)大于推進(jìn)劑與襯層的模量，在外界拉伸載荷作用下變形較小，絕熱層的厚度大小對結(jié)果影響較小，因此設(shè)置絕熱層的厚度為60 μm。推進(jìn)劑的厚度設(shè)置為700 μm，模型中推進(jìn)劑的尺寸大小為1000 μm×700 μm，滿足推進(jìn)劑代表性體積單元最小尺寸680 μm×680 μm的要求[17]。由于推進(jìn)劑內(nèi)部AP等顆粒的夾雜的原因，還需對推進(jìn)劑內(nèi)部進(jìn)行顆粒填充處理。推進(jìn)劑中顆粒的體積分?jǐn)?shù)63.6%，處理的方法基于分子動(dòng)力學(xué)算法[18]。由于相鄰顆粒之間間隙較小不利于網(wǎng)格單元的劃分，因此對分子動(dòng)力學(xué)方法生成的顆粒的位置進(jìn)行了調(diào)整，建立的粘接界面細(xì)觀填充模型及其尺寸如圖1所示。

圖1 粘接界面的細(xì)觀模型及其尺寸

1.2 顆粒的脫濕

在推進(jìn)劑內(nèi)部，由于外界拉伸載荷作用，導(dǎo)致顆粒/粘合劑基體之間界面存在脫粘現(xiàn)象。對于界面脫粘類問題，可采用粘性接觸的方法來模擬[12]。粘性接觸基于面面接觸來定義界面損傷，通常采用牽引分離定律作為其本構(gòu)，比如內(nèi)聚力模型等。內(nèi)聚力模型定義了界面力與界面位移之間的關(guān)系，廣泛用于模擬界面脫粘類問題。常用的內(nèi)聚力模型有雙線性內(nèi)聚力模型，指數(shù)型內(nèi)聚力模型，多項(xiàng)式型內(nèi)聚力模型等[19]。雙線性內(nèi)聚力模型具有形式簡單，易于實(shí)現(xiàn)等優(yōu)點(diǎn)。因此，本文采用雙線性內(nèi)聚力模型，如圖2所示。

圖2 雙線性內(nèi)聚力模型

(1)

式中 下標(biāo)n、s分別表示法向與切向；Knn、Kss分別為界面的法向與剪切剛度；Tn、Ts分別為法向與剪切的界面力。

界面位移繼續(xù)增大，當(dāng)δ0≤δ≤δf時(shí)，界面產(chǎn)生損傷，該階段內(nèi)界面力隨著界面位移增加而線性減小，其關(guān)系為

(2)

D為界面損傷系數(shù)，如式(3)所示：

(3)

δf為界面失效位移， 當(dāng)δf≤δ時(shí)，界面完全損傷，界面損傷系數(shù)D=1，界面力減小為0。此時(shí)，再增加界面位移，界面力始終為0。界面的損傷起始準(zhǔn)則采用最大名義應(yīng)力準(zhǔn)則，該準(zhǔn)則認(rèn)為界面力達(dá)到界面的最大名義應(yīng)力時(shí)，界面損傷起始，如式(4)所示：

(4)

(5)

由上文可知，決定雙線性內(nèi)聚力模型形狀的參數(shù)為界面初始剛度、最大名義應(yīng)力、界面失效位移。由于缺乏細(xì)觀尺度下的界面相關(guān)參數(shù)，在經(jīng)過大量計(jì)算基礎(chǔ)上，發(fā)現(xiàn)采用表1所示界面參數(shù)的粘接界面損傷形貌計(jì)算結(jié)果與實(shí)際比較吻合。

表1 顆粒/基體界面參數(shù)

1.3 材料的本構(gòu)與邊界條件設(shè)置

將AP顆粒視為線彈性材料，對絕熱層、襯層等進(jìn)行單向拉伸試驗(yàn)，取其初始模量作為其彈性模量，各組分的參數(shù)如表2所示。

表2 粘接界面各組分力學(xué)性能參數(shù)

邊界條件的設(shè)置與實(shí)際拉伸過程一致，由于宏觀尺度下襯層的厚度比較小，因此細(xì)觀尺度下，只考慮界面法向的變形，不考慮沿平行于界面方向的變形。設(shè)置AB、CD邊為x方向固定，BC邊為y方向固定，AD邊沿y方向拉伸。網(wǎng)格劃分與邊界條件的設(shè)置如圖3所示。

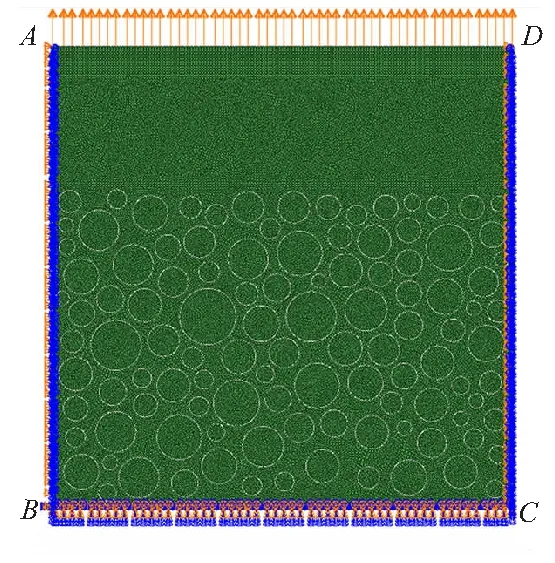
圖3 網(wǎng)格劃分與邊界條件的設(shè)置

2 計(jì)算結(jié)果分析

2.1 粘接界面的變形演化過程

定義拉伸位移與模型邊長之比為外界拉伸應(yīng)變，定量地分析粘接界面的變形過程。外界拉伸應(yīng)變10%數(shù)值模擬結(jié)果與試驗(yàn)結(jié)果對比如圖4所示。

(a)Experiment result (b)Numerical result

圖4(a)[7]、(b)分別為試驗(yàn)結(jié)果與數(shù)值模擬結(jié)果粘接界面的細(xì)觀形貌。可見，試驗(yàn)結(jié)果和數(shù)值模擬結(jié)果中，在粘接界面推進(jìn)劑一側(cè)，由于顆粒脫濕與脫濕之后基體的損傷，在推進(jìn)劑內(nèi)部形成一條局部“損傷帶”。數(shù)值模擬結(jié)果的損傷形貌與試驗(yàn)結(jié)果比較吻合，建立的粘接界面細(xì)觀數(shù)值模型能較好地反映粘接界面細(xì)觀損傷過程。

不同外界拉伸應(yīng)變下粘接界面的Von Mises應(yīng)力演化過程如圖5所示。可見，由于顆粒夾雜的原因，粘接界面內(nèi)部的Von Mises應(yīng)力不是均勻分布的，顆粒內(nèi)部的Von Mises應(yīng)力較大，其他區(qū)域的較小。外界拉伸應(yīng)變2%(圖5(a))，顆粒與粘合劑基體界面保持結(jié)構(gòu)完好。外界拉伸應(yīng)變3.2%(圖5(b))，推進(jìn)劑內(nèi)部部分大顆粒開始“脫濕”，在顆粒與粘合劑基體之間形成微裂縫。外界拉伸應(yīng)變5.0%(圖5(c))，顆粒脫濕的尺寸增大，微裂縫繼續(xù)擴(kuò)展。外界拉伸應(yīng)變5.7%(圖5(d))，推進(jìn)劑內(nèi)部粘合劑基體比較薄弱位置處的Von Mises應(yīng)力急劇增大，遠(yuǎn)高于周邊區(qū)域，“脫濕”形成的微裂縫匯聚在推進(jìn)劑局部區(qū)域形成一個(gè)較大的裂縫。外界拉伸應(yīng)變從5.9%增加至6.0%(圖5(e)～圖5(f))，推進(jìn)劑內(nèi)部局部區(qū)域的裂縫繼續(xù)擴(kuò)展，在推進(jìn)劑內(nèi)部形成一條“損傷帶”，該損傷帶內(nèi)的粘合劑基體發(fā)生較大變形，Von Mises應(yīng)力遠(yuǎn)高于周邊區(qū)域。

(a)2.0% (b)3.2% (c)5.0%

不同外界拉伸應(yīng)變下粘接界面的最大主應(yīng)變演化過程如圖6所示。

(a)2.0% (b)3.2% (c)5.0%

由圖6可見，與Von Mises應(yīng)力一樣，粘接界面內(nèi)部的最大主應(yīng)變也是不是均勻分布的。外界拉伸應(yīng)變從2%增加至3.2%(圖6(a)、(b))，粘接界面內(nèi)部最大主應(yīng)變的分布趨勢不變，但數(shù)值隨外界拉伸應(yīng)變的增大而增大。外界拉伸應(yīng)變5.0%～5.7%(圖6(c)、(d))，顆粒“脫濕”以后，相鄰“脫濕”顆粒之間的粘合劑基體的最大主應(yīng)變開始增大。外界拉伸應(yīng)變5.0%～5.7%(圖6(e)、(f))，在推進(jìn)劑一側(cè)“局部化”區(qū)域的最大主應(yīng)變遠(yuǎn)高于周邊。

對上述粘接界面顆粒“脫濕”局部區(qū)域進(jìn)行放大處理，最大主應(yīng)力分布如圖7所示。可見，顆粒“脫濕”之前，粘接界面內(nèi)部的最大主應(yīng)力分布比較均勻，應(yīng)力集中現(xiàn)象不明顯。顆粒“脫濕”之后，位于相鄰顆粒之間的粘合劑基體的薄弱環(huán)節(jié)處，最大主應(yīng)力較周邊區(qū)域大，該處存在明顯的應(yīng)力集中現(xiàn)象，方向與基體拉伸方向相同，對粘合劑基體形成“拉扯”作用，使其發(fā)生較大變形，使該處成為薄弱環(huán)節(jié)。

(a)Before dewet

2.2 粘接界面的失效模式

粘接界面外界拉伸應(yīng)變與應(yīng)力之間的關(guān)系如圖8所示。可知，粘接界面的應(yīng)力變化隨外界拉伸應(yīng)變的變化可分為三個(gè)階段：線性段上升段(Strain<3.2%)，非線性上升段(3.2%5.7%)。與前文不同拉伸應(yīng)變下粘接界面的細(xì)觀形貌進(jìn)行對比，分析造成這種現(xiàn)象的原因。

圖8 粘接界面的應(yīng)力應(yīng)變曲線

線性上升段，外界拉伸應(yīng)變從0增加至3.2%，應(yīng)力從0增加至0.181 MPa，該階段由于外界拉伸應(yīng)變較小，粘接界面內(nèi)部的應(yīng)力不足以使推進(jìn)劑內(nèi)部顆粒發(fā)生“脫濕”，推進(jìn)劑內(nèi)部顆粒與粘合劑基體粘接良好，粘接界面的應(yīng)力表現(xiàn)為隨外界拉伸應(yīng)變的增加而線性增加，在宏觀尺度下表現(xiàn)為線彈性。

非線性上升段，外界拉伸應(yīng)變從3.2%增加至5.7%，應(yīng)力從0.181 MPa增加至0.225 MPa，該階段內(nèi)，隨外界拉伸應(yīng)變的增加，推進(jìn)劑內(nèi)部顆粒/粘合劑基體界面處的應(yīng)力達(dá)到其最大名義應(yīng)力，造成顆粒/粘接劑基體界面開始發(fā)生損傷，其粘接能力減弱，推進(jìn)劑內(nèi)部顆粒開始脫濕，造成粘接界面的應(yīng)力隨應(yīng)變增加的速率開始減慢，表現(xiàn)出非線性的特點(diǎn)。

下降段，該階段內(nèi)，推進(jìn)劑內(nèi)部顆粒/基體界面的損傷程度繼續(xù)增大，界面承受載荷作用的能力繼續(xù)減弱，基體承受的載荷增大，同時(shí)基體開始損傷，在推進(jìn)劑內(nèi)部比較薄弱的區(qū)域，損傷開始加劇，形成一個(gè)局部化的損傷區(qū)域，應(yīng)力迅速下降。

由前文可知，推進(jìn)劑中顆粒脫濕之后，粘合劑基體受到的載荷急劇增大，可能在粘合劑基體內(nèi)部造成損傷。對于粘合劑基體的損傷，常用的損傷準(zhǔn)則包括Von Mises應(yīng)力準(zhǔn)則，最大主應(yīng)力準(zhǔn)則等。假設(shè)粘合劑基體是各向同性均勻材料，只有在拉伸條件下才會(huì)導(dǎo)致?lián)p傷，而在壓縮條件下，基體不會(huì)產(chǎn)生損傷。而Von Mises應(yīng)力受壓狀態(tài)與受拉狀態(tài)數(shù)值相等時(shí)，都會(huì)導(dǎo)致粘合劑基體損傷的結(jié)論，使結(jié)果不準(zhǔn)確，所以本文采用最大主應(yīng)力準(zhǔn)則。認(rèn)為粘合劑基體內(nèi)部的最大主應(yīng)力達(dá)到失效應(yīng)力時(shí)，單元發(fā)生損傷，如式(6)所示。

σmax_principle=σf

(6)

設(shè)置粘合劑基體的最大失效應(yīng)力σf=0.45 MPa[20]。定義狀態(tài)變量SDV1為損傷變量，當(dāng)粘合劑基體損傷時(shí)，令SDV1=1。

粘接界面的失效過程如圖9所示。外界拉伸應(yīng)變?yōu)?.7%時(shí)(圖9(a))，SDV1始終等于0，粘合劑基體內(nèi)部沒有損傷，粘接界面的損傷形式主要為推進(jìn)劑內(nèi)部顆粒的脫濕。外界拉伸應(yīng)變5.9%時(shí)(圖9(b))，顆粒脫濕尺寸繼續(xù)增大，部分相鄰“脫濕”顆粒之間的粘合劑基體開始損傷，損傷變量SDV1極值約0.5。外界拉伸應(yīng)變從6.0%增加至9.5%(圖9(c)、(f))，隨外界拉伸應(yīng)變的增大，發(fā)生損傷的粘合劑基體單元不斷增多，損傷的區(qū)域逐漸擴(kuò)展。外界拉伸應(yīng)變?yōu)?.5%時(shí)，幾乎貫穿粘接界面推進(jìn)劑一側(cè)，最終使粘接界面失效。

(a)5.7% (b)5.9% (c)6.0%

3 結(jié)論

(1)數(shù)值模擬結(jié)果損傷形貌與試驗(yàn)結(jié)果比較吻合，建立的粘接界面細(xì)觀數(shù)值模型能較好地反映其細(xì)觀損傷過程，數(shù)值模擬結(jié)果對預(yù)測粘接界面的力學(xué)性能具有參考意義。

(2)初始粘接良好的粘接界面的損傷與失效經(jīng)歷了一個(gè)局部化過程。其損傷模式表現(xiàn)為：當(dāng)外界拉伸應(yīng)變比較小時(shí)，界面的損傷形式主要為推進(jìn)劑內(nèi)部顆粒的脫濕，分布比較均勻；繼續(xù)增加外界拉伸應(yīng)變，推進(jìn)劑一側(cè)比較薄弱的粘合劑基體局部區(qū)域損傷開始增大，損傷沿薄弱區(qū)域的擴(kuò)展最終貫穿整個(gè)粘接界面，使粘接界面失效。

(3)粘接界面在拉伸過程中，顆粒的脫濕與粘合劑基體的損傷導(dǎo)致了粘接界面應(yīng)力應(yīng)變曲線的非線性。為提高粘接界面抵抗脫粘的能力，一方面應(yīng)提高推進(jìn)劑內(nèi)部顆粒與粘合劑基體的最大粘接強(qiáng)度；另一方面，顆粒脫濕之后，提高粘合劑基體的最大失效應(yīng)力。