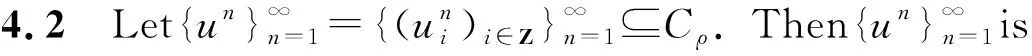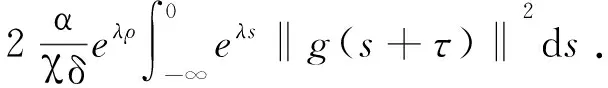Pullback attractors for lattice FitzHugh-Nagumo systems with fast-varying delays
-
(School of Mathematics, Southwest Jiaotong University, Chengdu 610031, China)
Abstract: We investigate the dynamical behavior of lattice FitzHugh-Nagumo equations with fast-varying delays and prove the existence and uniqueness of pullback attractor for the equations. Generally,studying the attractors of time-varying delay equations require that the derivative of the delay term is less than 1 (slow-varying delay). In this paper, by using some differential inequality techniques, we remove this constraint. Thus our method can be used to deal with equations with fast-varying delays.
Keywords: Global attractor; Lattice; FitzHugh-Nagumo system; Fast-varying delay
1 Introduction
Lattice differential equations have many applications where the spatial structure has a discrete character.Wangetal.[1]used the idea of ‘tail ends’ estimates on solutions and obtained a result concerning the existence of a global attractor for a class of reaction-diffusion lattice systems. Later on, their results were extended to various problems, see for instance,Refs.[2-11]. The FitzHugh-Nagumo system arises as a model describing the signal transmission across axons in neurobiology[12]. The asymptotic behavior of a FitzHugh-Nagumo system was investigated in Refs.[13-15]. The results were extended to stochastic, see for instance Refs.[16-17]. Since time-delays are frequently encountered in many practical systems, which may induce instability, oscillation and poor performance of systems, delay lattice systems then arise naturally while these delays are taken into account. Recently, attractors of delay lattice systems have been considered in Refs.[18-24]. The existing results of studying attractors for time-varying delay equations require that the derivative of the delay term be less than 1(slow-varying delay). By using differential inequality technique, our results remove the constraints on the delay derivative.So we can deal with the lattice FitzHugh-Nagumo systems with fast-varying delays (without any constraints on the delay derivative).
Motivated by the discussions above, we study the dynamical behavior of the following lattice FitzHugh-Nagumo system with fast-varying delays: forτ∈Randi∈Z,
hi(ui(t-ρ0(t)))-αvi+fi(t),t>τ
(1)
(2)
with the initial condition
ui(τ+s)=φi(s),vi(τ)=φi,s∈[-ρ, 0]
(3)
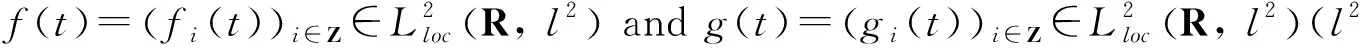
This paper is organized as follows. In Section 2, we prove that the lattice system (1)-(3) generates a non-autonomous dynamical system. In Section 3, we derive a priori estimates on the solutions to (1)-(3). In Section 4, we proof the existence and uniqueness of pull-back attractor for the lattice systems.
2 Priori estimates
In this section,we establish the existence of a continuous non-autonomous dynamical system generated by System (1)-(3) and derive some priori estimates which will be needed for proofing the existence of a global attractor. We formulate System (1)-(3) as an abstract ordinary differential equation. To this end, we denote byl2the Hilbert space defined by

(Bu)i=ui+1-ui,
(B*u)i=ui-1-ui,
(Au)i=-ui-1+2ui-ui+1,
for eachi∈Z. Then
A=BB*=B*B,
(B*u,v)=(u,Bv),u,v∈l2.
Denote
φ(s)={φi(s)}i∈Z,s∈[-ρ,0]
andφ={φi}i∈Z.Denote byutthe function defined on [-ρ,0] according to the relation
ut(s)=(uit(s))i∈Z=(ui(t+s))i∈Z=
u(t+s),s∈[-ρ,0],
and letCρ=C([-ρ,0],l2) with the maximum norm
Then System(1)-(3) can be rewritten as
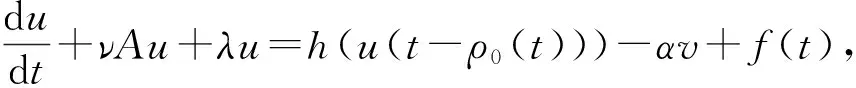
t>τ
(4)
(5)
with the initial condition
u(τ+s)=φ(s),v(τ)=φ,s∈[-ρ,0]
(6)
whereu=(ui)i∈z,
h(u(t-ρ0(t)))=hi(ui(t-ρ0(t)))i∈z,
f(t)=(fi(t))i∈z,g(t)=(gi(t))i∈z,
φ=(φi)i∈zandφ=(φi)i∈z. We make the following assumptions onhi,i∈Z. For eachi∈Z,hiis a nonlinear function satisfying the following assumption:
(H)hi(0)=0 andhiis Lipschitz continuous uniformly with respect toi, that is, there is a positive constantL, independent ofi, such that for alls1,s2∈R,
|hi(s1)-hi(s2)|≤L|s1-s2|.
In fact, by (H) we find that
‖h(u)-h(v)‖≤L‖u-v‖,u,v∈l2.
Then it follows from the standard theory of ordinary differential equations that there exists a unique local solution (u,v) for System (4)-(6). The following estimates imply that the local solution is actually defined globally.In the sequence, we assume that
(7)
Lemma2.1Assume that (H) and (7) hold. Then for everyτ∈R,T>0,φ∈Cρandφ∈l2, there exists a positive constantc=c(τ,T,φ,φ) such that the solution (u,v) of Problem (4)-(6) satisfies
(8)
ProofTaking the inner product of (4) withβuinl2, we find that
β(h(u(t-ρ0(t))),u)-βα(u,v)+β(u,f(t))
(9)
Taking the inner product of(5) withανinl2,we get that
α(v,g(t))
(10)
Summing up (9) and (10), we get
βλ‖u‖2+αδ‖v‖2=β(h(u(t-ρ0(t))),
u)+β(u,f(t))+α(v,g(t))
(11)
We now estimate the right-hand side of (11). The first term is bounded by
|β(h(u(t-ρ0(t))),u)|≤
β‖h(u(t-ρ0(t))‖‖u‖≤
(12)
For the left two term on the right-hand side of (11), we have
(13)
By (11)-(13) we obtain
(14)
Letσ=min{λ,δ}. Then it follows from (14) that
-σ(β‖u‖2+α‖v‖2)+
(15)
By Gronwall inequality, that fort≥τ, we have
β‖u(t)‖2+α‖v(t)‖2≤
e-σ(t-τ)(β‖φ(0)‖2+α‖φ‖2)+
(16)
From the condition (7), by using continuity, we obtain that there exist positive constantsμ<σandNsuch that ‖φ‖ρ+‖φ‖≤Nand
(17)
hold. Then we prove that fort≥τ
β‖u(t)‖2+α‖v(t)‖2≤
dNe-μ(t-τ)+(1-η)-1I(t)
(18)
where
To this end, we first prove for anyd>1,
β‖u(t)‖2+α‖v(t)‖2<
dNe-μ(t-τ)+(1-η)-1I(t),t≥τ
(19)
If (19) is not true, then, from ‖φ‖ρ+‖φ‖≤Nand‖u(t)‖ and ‖v(t)‖ are continuous, there must be at*>τsuch that
β‖u(t*)‖2+α‖v(t*)‖2≥
dNe-μ(t*-τ)+(1-η)-1I(t*)
(20)
and
β‖u(t)‖<
dNe-μ(t-τ)+(1-η)-1I(t),τ-ρ≤t (21) Hence, it follows from (16) (17) (20) and (21) that β‖u(t*)‖2+α‖v(t*)‖2≤ e-σ(t*-τ)(β‖φ(0)‖2+α‖φ‖2)+ e-μ(t*-τ)(β‖φ(0)‖2+α‖φ‖2)+ (1-η)-1I(t*))ds+ e-μ(t*-τ)(β‖φ(0)‖2+α‖φ‖2)+ η(1-η)-1I(t*)+I(t*)≤ dNe-μ(t*-τ)+(1-η)-1I(t*) (22) which contradicts inequality(20). So inequality (19) holds for allt≥τ. Lettingd→1 in inequality (19), we have inequality (18).The proof is complete. Lemma 2.1 implies that the solutionuis defined in any interval of [τ,T+τ) for anyT>0. It means that this local solution is, in fact, a global one. Givent∈R, define a translationθtonRby θt(τ)=τ+t,τ∈R (23) Then {θt}t∈Ris a group acting onR. We now define amapping Φ:R+×R×Xρ→Xρ,for Problem (4)-(6), whereXρ=Cρ×l2. Givent∈R+,τ∈Rand Ψτ=(uτ,vτ)∈Xρ, let Φ(t,τ,Ψτ)=(ut+τ(·,τ,uτ), v(t+τ,τ,vτ)) (24) whereut+τ(s,τ,uτ)=u(t+τ+s,τ,uτ),s∈[-ρ,0].By the uniqueness of solutions, we find that for everyt,s∈R+andτ∈Rand Ψτ∈Xρ, Φ(t+s,τ,Ψτ)=Φ(t,s+τ, (Φ(s,τ,Ψτ))). Then we see that Φ is a continuous non-autonomous dynamical system onXρ. In the following two sections, we will investigate the existence of a pullback attractor for Φ. To this end, we need to define an appropriate collection of families of subsets ofXρ.LetBρ={Bρ(τ):τ∈R}be a family of nonempty subsets ofXρ.ThenBρis called tempered (or subexponentially growing) if for everyc>0, the following holds: wherex=(φ,φ).In the sequel, we denote byDρthe collection of all families of tempered nonempty subsets ofXρ, i.e., Dρ={Bρ={Bρ(τ):τ∈R}:Bρis tempered}. From the condition (7), by using continuity, we obtain that there exists a positive constantμ<σsuch that (25) holds. The following condition will be needed when deriving uniform estimates of solutions: ∞,?τ∈R (26) In this section, we derive uniform estimates of solutions of Problem(4)~(6) which are needed for proving the existence and uniqueness of pullback attractor for Problem (4)~(6). The estimates of solutions of Problem (4)~(6) inXρare provided below.The symbolcis a positive constant which may change its value from line to line. Lemma3.1Assume that (H), (7) and (26) hold. Then for everyτ∈RandDρ={Dρ(τ):τ∈R}∈Dρ, there existsT=T(τ,Dρ)>ρsuch that for allt≥Tand (φ,φ)∈Dρ(τ-t), the solution (u,v) of (4)-(6) satisfies (27) whereχ=min{α,β}. ProofReplacingtandτin (15) by ? andτ-t, respectively, we have for ?>τ-t, α‖v(?,τ-t,φ)‖2)≤ -σ(β‖u(?,τ-t,φ)‖2+ α‖v(?,τ-t,φ)‖2)+ (28) For simplicity, we denoteu(?)=u(?,τ-t,φ)andv(?)=v(?,τ-t,φ). Then, let us define functions V(?)=eμ?(β‖u(?)‖2+α‖v(?)‖2), ?≥τ-t-ρ, wherev(?)=0, ?∈[τ-t-ρ,τ-t), and Now, we claim that V(?)≤U(?), ?≥τ-t (29) If inequality (29) is not true, from the fact thatV(?) andU(?) are continuous, then there must be a ?*>τ-tsuch that V(?) (30) V(?*)=U(?*) (31) where ?*?inf{?>τ-t|V(?)>U(?)}, and there is a sufficiently small positive constantΔ? such that V(?)>U(?), ?∈(?*, ?*+Δ?) (32) Calculating the upper right-hand Dini derivative ofV(?) at ? and considering (31) and (32), we obtain (33) On the other hand, it follows from (28), we have D+V(?*)=μeμ?*(β‖u(?*)‖2+ α‖v(?*)‖2)+eμ?*D+(β‖u(?*)‖2+ α‖v(?*)‖2)≤(μ-σ)eμ?*(β‖u(?*)‖2+ (34) Noticing thatU(?) is monotone nondecreasing on [τ-t-ρ, +∞), this, together with (30) and (31), yields V(?*-ρ0(?*))< U(?*-ρ0(?*)) (35) which implies β‖u(?*-ρ0(?*))‖2≤ eμρ(β‖u(?*)‖2+α‖v(?*)‖2) (36) It follows from (25) (34) and (36) that which contradicts (33). Until now, (29) has been proven to be true. Thus we get fort>ρand -ρ≤ξ≤0, β‖u(τ+ξ,τ-t,φ)‖2+ α‖v(τ,τ-t,φ)‖2≤ Since (φ,φ)∈Dρ(τ-t)∈Dρ, we find that for everyτ∈RandDρ∈Dρ, there existsT=T(τ,Dρ)>ρsuch that for allt≥Tand -ρ≤ξ≤0, β‖u(τ+ξ,τ-t,φ)‖2+ α‖v(τ,τ-t,φ)‖2≤ This completes the proof. Lemma3.2Assume that (H),(7) and (26) hold. Then for everyτ∈R,Dρ={Dρ(τ):τ∈R}∈Dρandε>0, there existT=T(τ,Dρ,ε)>ρandN=N(τ,Dρ,ε) such that for allt≥Tand (φ,φ)∈Dρ(τ-t), the solution (u,v) of (4)~(6) satisfies |vi(τ, τ-t, φ)|2)≤ε (37) (38) (39) Summing up (38) and (39), we get (40) We now estimate the terms in (40) as follows. First, we have By the property of the functionθ, we have which implies that (41) We now estimate the right-hand side of (40). The first term is bounded by (42) For the left two term on the right-hand side of(40), we have (43) By (40)~(43) we obtain (44) Letσ=min{λ,δ}. It follows that (45) Futher, (46) By the similar argument as in Lemma 3.1, we get from (46) for anyt>ρand -ρ≤ξ≤0, α|vi(τ, τ-t, φ)|2)≤ (47) It follows from Lemma 3.1 that for anyτ∈R, (φ,φ)∈Dρ,ε>0 there existT=T(τ,Dρ,ε)>ρandK1=K1(τ,Dρ,ε)such that fork≥K1,t≥Tand -ρ≤ξ≤0 (48) which, together with (47), implies α|vi(τ,τ-t,φ)|2)≤ (49) We have from (φ,φ)∈Dρ(τ-t) that there existsT1=T1(τ,Dρ,ε)>0 such that for allt≥T1and -ρ≤ξ≤0, (50) We have from (26) that there is aN1=N1(τ,ε)>0 such that for allk≥N1, (51) Note that α|vi(τ,τ-t,φ)|2)≤ α|vi(τ,τ-t,φ)|2), which along with (49)~(51) we conclude the proof. In this section, we establish the existence ofDρ-pullback attractor for the non-autonomous dynamical system Φ associated with the problem (4)~(6). Lemma4.1Assume that (H) (7) and (26) hold. Then for everyτ∈RandDρ={Dρ(τ):τ∈R}∈Dρ, there existsT=T(τ,Dρ)>ρsuch thatusatisfies thatuτ(·,τ-t,φ) is equicontinuous inl2. ProofDenote byPku=(u1,u2,...,uk,0, 0,...), foru∈l2andk∈N. By Lemma 3.2, forε>0, there existsT=T(τ,ε)>ρand large enough integerN=N(τ,ε) such that for allt≥T, (52) Letu1=PNu. By Lemma 3.1, it follows from (4) and the equivalence of norm in finite dimensional space that there existsT=T(τ)>ρsuch that for allt≥T, (53) wherec=c(τ) is a positive number. Without loss of generality, we assume thats1,s2∈[-ρ, 0] with 0 ‖u1(τ+s1,τ-t,φ)-u1(τ+s2,τ-t,φ)‖≤ (54) which implies that there exits a constantζ=ζ(ε)>0 such that if |s1-s2|<ζ, then ‖u(τ+s2,τ-t,φ)- which along with (52) implies that for allt≥T, ‖u(τ+s2,τ-t,φ)-u(τ+s1,τ-t,φ)‖≤ ‖PNu(τ+s2,τ-t,φ)- PNu(τ+s1,τ-t,φ)‖+ ‖(I-PN)u(τ+s2,τ-t,φ)‖+ ‖(I-PN)u(τ+s1,τ-t,φ)‖≤ε. This completes the proof. As for the compactness inl2in Ref.[16] one can easily verify the the following compactness criteria inCρ=C([-ρ, 0],l2) by means of uniform tail estimates. Theorem4.3Assume that (H), (7) and (26) hold. Then, the non-autonomous dynamical system Φ has a uniqueDρ-pullback attractorAρ={Aρ(τ):τ∈R}∈Xρ. ProofForτ∈R, denote by M(τ)}, where Firstly, we know from Lemma 3.1 that Φ has aDρ-pullback absorbing setK(τ).Secondly, since Lemma 3.1, 3.2 and 4.1 coincide with all the conditions of Lemma 4.2, Φ isDρ-pullback asymptotically compact inXρ. Hence the existence of a uniqueDρ-pullback attractor for the non-autonomous dynamical system Φ follows from Proposition 2.7 in Ref.[18] immediately.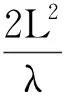
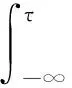
3 Uniform estimates of the solutions
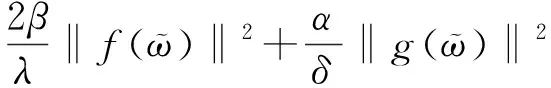
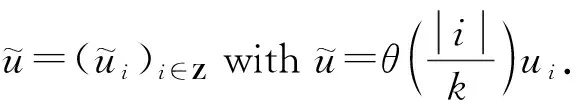
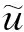
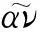
4 Existence of pullback attractors