一種改進的深度確定性策略梯度網絡交通信號控制系統

劉利軍, 王 州 , 余 臻

(1.廈門大學航空航天學院, 廈門 361101; 2. 廈門大學深圳研究院, 深圳 518057)

1 引 言

隨著全球人口的快速增長,以及城市化進程的發展,專家預計21世紀的城市人口將急劇增加.當務之急是城市有效地管理其基礎設施以應對這一問題.設計現代化城市時,一個關鍵的考慮因素是開發智能交通管理系統.交通管理系統的主要目標是減少交通擁堵.高效的城市交通管理能夠節省時間和財務,并減少二氧化碳等大氣污染物排放到大氣中[1].已經有許多學者提出方案解決這個問題[2].主要道路的交叉路口一般是通過交通信號燈管理.低效率的交通信號燈控制會導致許多浪費,增加車輛發生事故的風險[3]. 現有的交通燈控制信號按照固定程序不考慮實時交通流量,效率低.因此，研究人員提出了許多改進方案,這些方案可以分為三類:第一類是預定控制程序,參考歷史數據制定交通信號切換時間; 第二類是利用傳感器檢測來往車輛,用以延長或縮短信號切換時間; 第三類是自適應信號控制,根據交叉路口的當前狀態自動切換[4].本論文對第三類控制方法展開研究,利用深度強化學習方法設計一種十字路口交通信號智能控制方法.

近年來，很多研究者結合深度學習和強化學習技術來處理復雜的優化問題,例如Atari 2600游戲[5],圍棋[6]等.1997 年Thorpe[7]首次將強化學習的方法應用到交通信號控制,大家開始意識到強化學習為解決非線性、不確定性的復雜路網問題提供了一種新的思路.隨著人工智能的快速發展,深度強化學習被應用到交通控制中.2016年Li等人將深度強化學習應用于交通信號控制中,降低了車輛14%的等待時間[8].2018年Liang等人[3]改進Dueling DQN[9]和DoubleDQN[10],將車輛等待時間降低了25.7%. 本論文通過分析交通環境特點, 設計了特征強化策略梯度算法(Feature Enhance DDPG，FEPG)算法并將其應用于交通信號控制系統中.

2 背 景

2.1 強化學習

強化學習的基本結構由智能體Agent和外界環境組成. Agent通過執行動作,從環境獲得下一狀態和獎勵值.不斷循環該過程,直到滿足一定條件為止.通常一個強化學習問題可以視為馬爾可夫決策過程(Markov Decision Process，MDP)[11]. MDP將強化學習任務定義為元組.其中，S是環境狀態的集合；A是Agent的動作空間集合；P是狀態之間的轉移概率；R是獎勵函數；γ∈[0,1]是獎勵值的折扣因子. Agent從狀態s采取動作a達到狀態s′并獲得獎勵r表示為(s,a,rt,s′).我們將Agent執行動作的方法稱之為策略π.強化學習的目標是最大化累積獎勵. 式(1)定義了累積獎勵Rt.下標t表示Agent執行策略π的第t步.

(1)

以累積獎勵為出發點,誕生了基于值的強化學習方法如Q-learning[12]等. 利用神經網絡擬合Q函數.在策略π下Q函數的定義為式(2).

Qπ(s,a)=E[Rt|st=s,at=a,π]

(2)

結合卷積神經網絡(Convolutional Neural Networks，CNN)[13],循環神經網絡(Recurrent Neural Network，RNN)[14]強化學習的應用場景變得更為豐富.谷歌DeepMind工作室[15]于2015年提出了結合基于值的和基于策略方法優點的深度確定性策略梯度算法(Deep Deterministic Policy Gradient,DDPG).本論文將改進DDPG網絡利用特征增強算法和樣本去重環節提升網絡性能，最后，將算法應用于交通信號控制中.

2.2 交通環境模型

十字交叉路口交通環境十分復雜, 且交通信號燈的控制十分重要.本文利用SUMO[16]仿真環境驗證算法有效性.道路模型的參數如表1所示. 車輛的污染排放模型可參考文獻[17].

2.2.1狀態s描述 如圖1所示十字路口狀態模型.路口的4個車道被劃分為4個單元,每個單元的長度為50 m. 單元格下方有白,灰色兩個方格.若某個單元內有n輛車,白色方格內數字則為n, 灰色方格代表該單元內車輛的平均速度,若n為0則平均速度取0, 否則取n輛車速度的平均值如式(3).因此狀態維度為32，如表2所示.

表2 狀態向量表

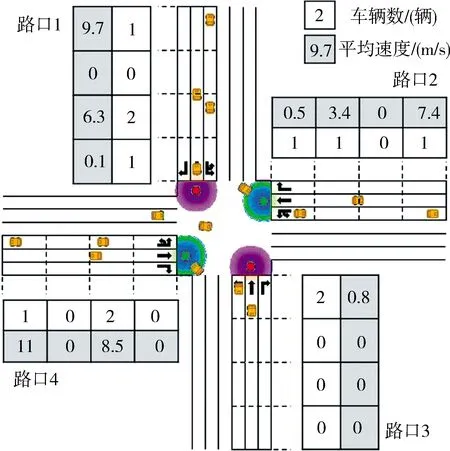
圖1 狀態描述Fig.1 State description

(3)

2.2.2動作a描述 如表3所示, 十字交叉路口的交通信號燈由6個信號相位組成.相位按順序從1號變化到6號不斷循環.每個相位由4個字母組成.每個字母代表一個路口信號燈的狀態. 其中:G為綠燈,允許通行;R為紅燈,禁止通行;Y為黃燈,注意通行.例如相位GRGR表示此時1、3路口綠燈,2、4路口紅燈. 將1和4相位時間作為動作a.考慮到車輛行駛速度,其范圍為5～50 s.其余相位設為安全的固定值.

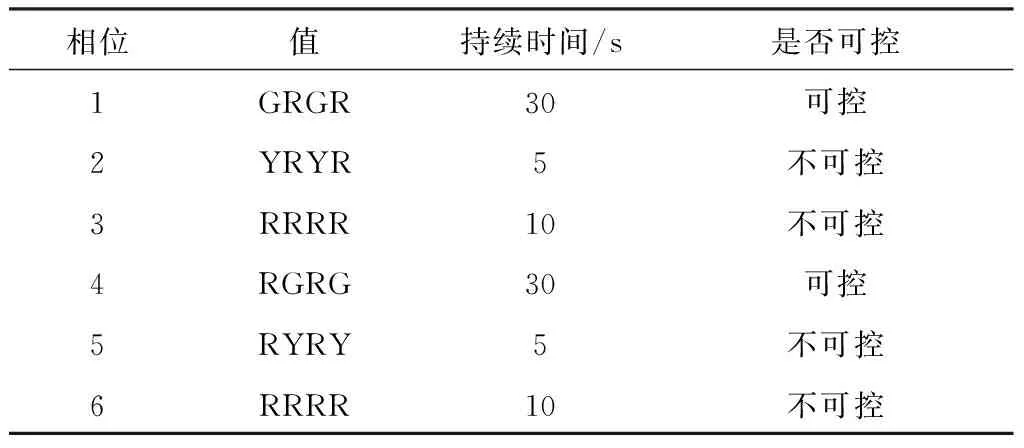
表3 交通信號相位

2.2.3獎勵值r描述 獎勵值在強化學習中的作用為提供網絡訓練方向,本論文目的為提高車輛在十字路口的通行效率,減少車輛等待時間.每輛車的等待時間定義為其行駛速度為0時所持續的時間,記作d,所有路口等待的所有車輛的累計等待時間記作D. 在t時刻的累計等待時間為Dt.獎勵值定義如式(4)所示.

(4)

其中,n,m為t,t+1時刻路口等待的車輛數目;k為常數;r越大, 代表減少的等待時間越多, 反之越少.算法的目的為盡量增大獎勵值r.

3 FEPG算法設計

DDPG網絡由策略網絡A,價值評價網絡C組成.其中策略網絡A分為A-online和A-target兩個網絡,其參數分別表示為θ,θ′.評價網絡分為C-online和C-target兩個網絡,其參數分別表示為φ,φ′.本論文針對交叉路口環境的特點提出兩點改進: (1) 交叉路口的狀態維度為32, 其中可能存在對訓練結果無貢獻維度. 利用基于信息增益的特征增強算法, 自動優化狀態; (2) 在DDPG算法中,經驗池是樣本的唯一來源,保持經驗池樣本的多樣性有利于網絡收斂. 網絡訓練時按照余弦相似度算法隨機丟棄樣本.本論文中將改進的DDPG網絡框架簡稱為FEPG(Feature Enhance DDPG)網絡,如圖2所示. FEPG算法首先從預訓練階段開始,預訓練階段的主要目的是進行原始樣本采集, 并應用特征增強算法和樣本去重算法.特征值增強和樣本去重算法的原理如下.

(1) 特征增強算法:由于交通環境的狀態量維度較高, 其中很可能存在干擾收斂的無關維度. 特征增強算法的核心思想是通過樣本的信息增益來篩選合適的特征. 將狀態s表示為向量s={x1,x2,...,x32}.特征篩選算法目的是降低不相關特征對訓練的影響. 經驗池在算法的預訓練階段將累積n組樣本. 對于隨機變量X, 可以求其信息熵:

(5)

以及給定條件Y下的條件熵:

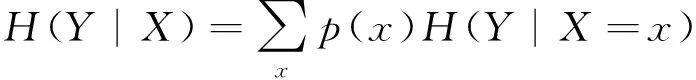
(6)

信息增益則可以表示為

IG(Y|X)=H(Y)-H(Y|X)

(7)

信息增益越大說明隨機變量X對于Y的貢獻越大. 信息增益用于計算離散變量, 因此將獎勵值和狀態離散化, 狀態的第i個維度的信息增益可以表示為

hi=IG(R|Xi)

(8)

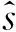
(9)

(10)

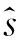
(2) 樣本去重算法:樣本去重的目的為保持樣本的多樣性, 加快算法收斂. 新進加入的樣本與樣本池中的樣本隨機比對相似度. 相似度越高, 樣本被丟棄的可能性越高.相似度利用樣本間的余弦值表示,丟棄概率表達式如式(11),其中α為丟棄系數.

(11)

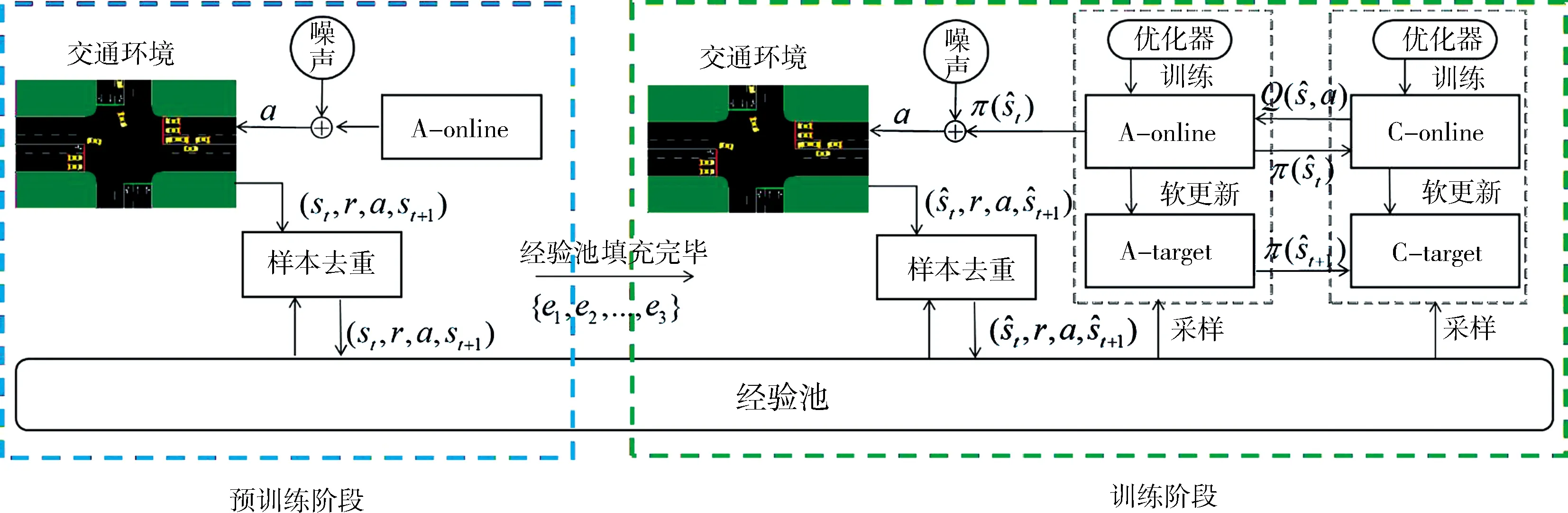
圖2 FEPG算法結構Fig.2 FEPG algorithm structure

待數據采集完畢后接著進入訓練階段.訓練階段中4個神經網絡相互作用,迭代.各個網絡的作用和相互之間的關系如下.

(12)

θ′←τθ+(1-τ)θ′

(13)

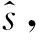
(14)

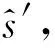
φ′←τφ+(1-τ)φ′

(15)

式(12)和式(14)中m為訓練batch大小,τ一般取0.01.以上對各個網絡的描述可以知道target網絡應當分別和online網絡具有相同的網絡結構.動作網絡在輸出時會添加均值為0,方差按指數規律衰減的高斯噪聲. 目的是鼓勵智能體在前期探索盡可能大的狀態空間.根據以上對網絡訓練方法的分析, FEPG算法流程如算法1所示.

算法1FEPG算法流程

1) 初始化在線網絡.并賦予隨機權重θ,φ

2) 初始化目標網絡θ′,φ′,初始化經驗池R

3) forj= 1 toMdo

4) 隨機初始化環境,獲得初始狀態s

5) fort= 1 toTdo

6) 動作網絡添加衰減的高斯噪聲輸出動作a

7) Agent執行動作a并獲得樣本存入經驗池

8) 根據式(11)進行樣本去重過程

9) if經驗池填充完畢

10) 根據式(8)和式(9)計算{ei}

11) if開始訓練

12) 在經驗池中采集m個樣本并計算.

13) 使用最小化方差更新在線價值網絡:

14) 使用策略梯度更新動作網絡:

15) 采用軟更新方式更新目標網絡:

θ′←τθ+(1-τ)θ′

φ′←τφ+(1-τ)φ′

16) endfor

17) endfor

4 實 驗

我們在上文所述的交通環境中驗證算法有效性, 并且對比定時控制FTC (Fixed Timing Control), Pang等人的DDPG[18]控制方法, Genders等人的DQN[19]控制方法與本文的FEPG控制方法. 其中FTC為傳統方法, DDPG和DQN為新型的強化學習方法.對比的核心指標為算法的收斂性能,車輛的平均等待時間以及車輛排放數據.

4.1 實驗設計與FTC方法

如表4所示, 本文設計了4組實驗, 分別是低車流密度低方差(Low Density Low Variance，LDLV), 低車流密度高方差(Low Density High Variance，LDHV), 高車流密度低方差(High Density Low Variance，HDLV), 高車流密度高方差 (High Density High Variance，HDHV). 車流密度指所有路口車輛數據, 方差指4個路口車流量值與平均值之差的平方和, 方差越高表示路口的車流密度差異越大. 車流密度數據可見文獻[20].

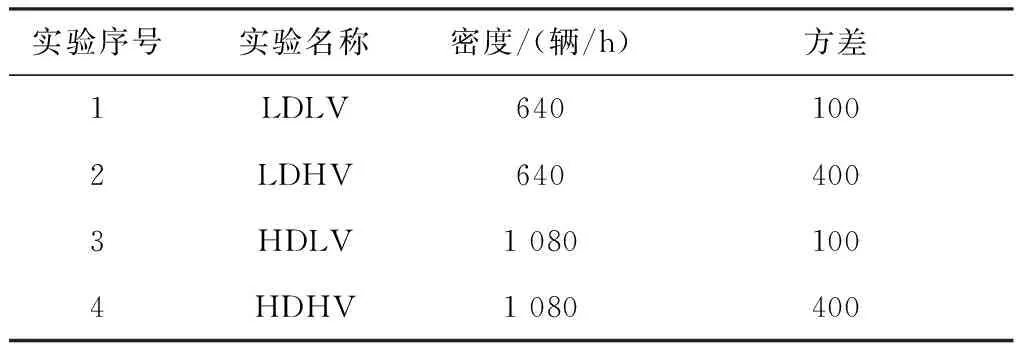
表4 車流類型

一般交通信號燈的相位采用FTC方法控制. 實驗測試不同環境下所有車輛的累積等待時間與1和4動作相位間隔的關系, 每個間隔時間測試2 000 s,統計結果如圖3所示. 在圖3中用綠色標記了交通累積等待時間較短的區間.針對4組實驗,將LDLV的固定間隔設置為30 s,LDHV的固定間隔設置為20 s, HDLV的固定間隔設置為35 s, HDHV的固定間隔設計為20 s.

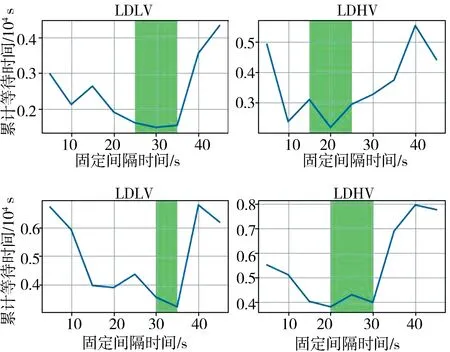
圖3 不同信號燈間隔的平均等待時間Fig.3 Average waiting time at different signal time intervals

4.2 實驗對比和結果分析

根據上文對環境的描述, 實驗的狀態維度為32,動作維度為1.設計FPPG網絡參數如表5所示. FEPG, DDPG, DQN算法的經驗池大小設為1萬,Batchsize為100,折扣取0.9. 訓練200輪,每輪執行200步后訓練結果如圖4所示.總體而言FEPG收斂最快性能最好, DDPG性能其次. DDPG控制算法中將每一個車道劃分為多個單元，且需要保證每個單元內僅有一輛車,狀態的維度為480. 其中很可能包含大量無效維度,導致其收斂不穩定,特別是在HDHV環境中表現不佳. DQN控制算法的輸出動作值為離散變量. 實驗中將輸出動作按5 s一個間隔進行劃分.其輸出量不連續無法精確控制, 導致其效果最差.

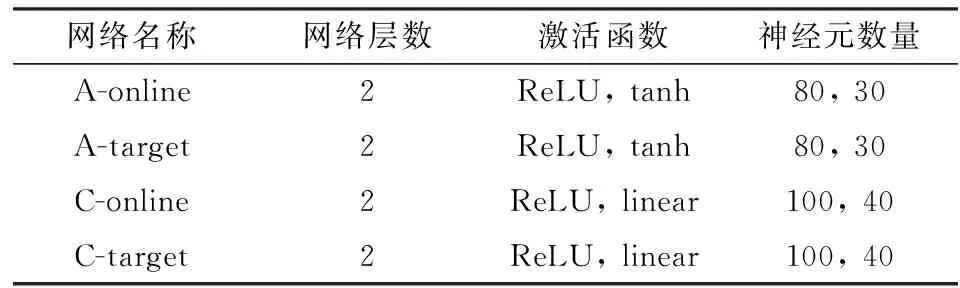
表5 網絡結構參數

將訓練完畢的網絡在4個實驗環境中進行測試, 測試時間為8 000 s. 圖5統計了8 000 s時間內不同算法每輛車的平均等待時間.LDLV和LDHV統計了約1 500輛車, HDLV和HDHV統計了約2 500輛車.統計結果表明FEPG算法控制下的車輛等待時間平均比BFI降低了23.5%, 比DQN算法降低9.8%, 比DDPG算法降低了7.6%. 結果表明FEPG算法學習到了如何高效的控制交通信號, 證明了算法的有效性.

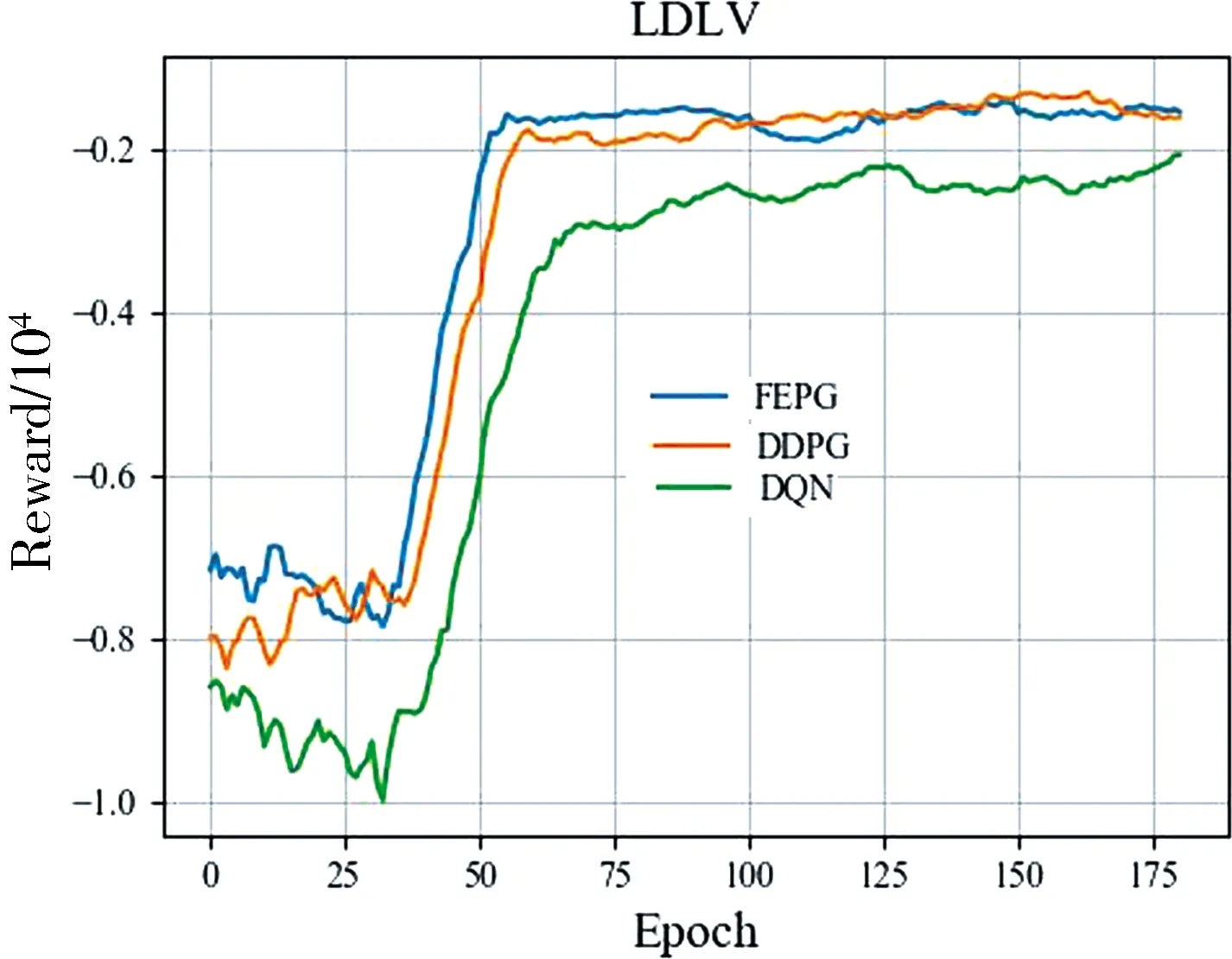
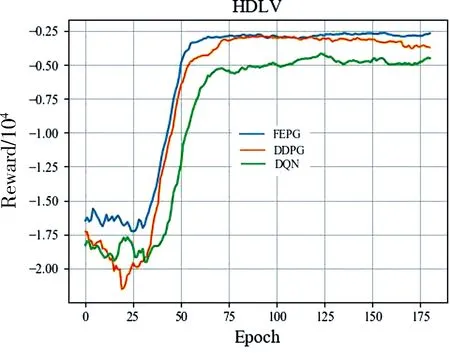
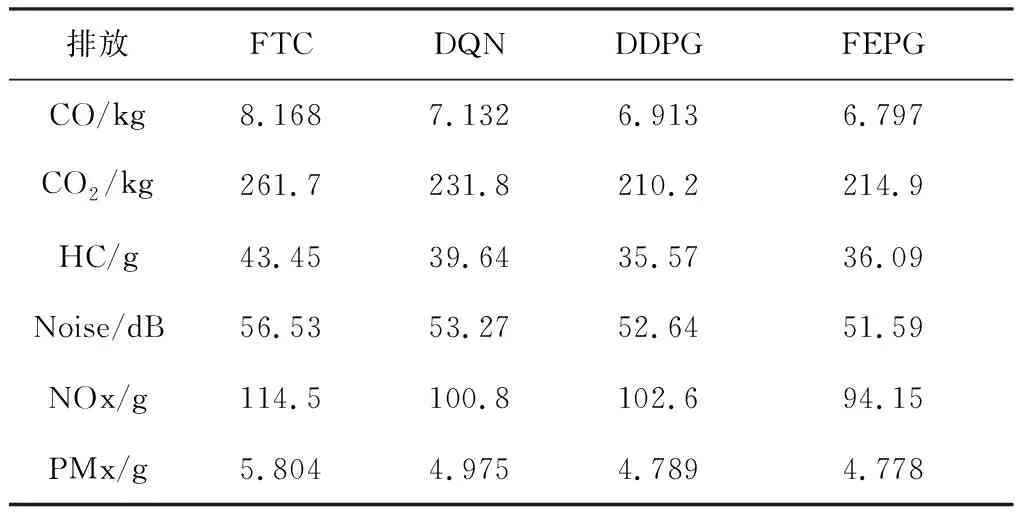
表6 污染物排放對比

以HDLV環境為例,表6是FEPG算法組對比其他算法在的污染排放情況.通過SUMO提供的數據統計了8 000 s內1 500輛車的污染排放情況. 依次是一氧化碳、二氧化碳、碳氫化合物、汽車噪音、氮氧化合物、和顆粒物排放.其中噪聲為8 000 s內平均值, 其余為累計值. 相比FTC算法, 使用FEPG算法使污染排放比FTC平均降低了19.7%, 比DQN算法降低了6.3%,比DDPG算法降低了3.6%.說明FEPG算法在提高通行效率的同時也降低了污染的排放.

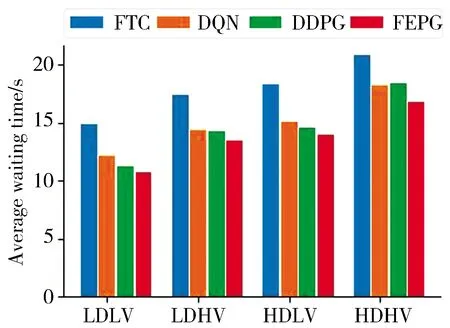
圖5 平均等待時間對比Fig.5 Comparisonof average waiting time

5 結 論

面對大城市日益嚴重的交通擁堵情況, 本論文設計了一種強化學習算法控制十字路口交通信號燈.基于DDPG算法結合特征增強算法和樣本去重算法設計了FEPG算法. 改進算法相比文獻[18]的DDPG算法和文獻[19]的DQN收斂的更快.以典型的十字路口交通信號燈為例,設計多組實驗驗證算法有效性. 實驗結果表明FEPG網絡在提高通行效率的同時也降低了汽車污染物排放.高效狀態特征選擇可以提高強化學習成功率, 交通環境中的數據多種多樣,后續研究的一個方向是如何在更加復雜的交通網絡中選取有效的環境特征.