航空減速器圓柱齒輪承載能力計算方法的分析

張麗娜,相 涯,丁金濤

(1.中國航發湖南動力機械研究所，湖南 株洲 412002; 2.直升機傳動技術國防科技重點實驗室，湖南 株洲 412002)

0 引 言

航空發動機減速器的設計不同于普通機械，對可靠性高和重量輕方面有較高要求。航空發動機減速器較多采用圓柱齒輪傳動，齒輪在減速器工作過程中起著傳遞動力、改變轉速和旋轉方向的重要作用，為減速器關鍵零部件之一。齒輪承載能力計算是減速器設計的核心。齒輪齒面接觸疲勞強度和齒根彎曲疲勞強度是考核齒輪承載能力和可靠性的一項重要性能指標。針對漸開線圓柱齒輪承載能力的評估方法，國際上較有影響的有：國際標準化組織(ISO)標準、美國齒輪制造協會(AGMA)標準、德國工業標準(DIN)標準、日本齒輪工業協會(JGMA)標準、前蘇聯國家(ΓOCT)標準等。國內現行有航空工業標準(HB)和國家標準(GB)各種計算方法的基本理論是相同的，且都以計算齒面接觸應力和齒根彎曲應力為主，但其形式上存在一定的差異，對影響輪齒強度的因素的考慮也不盡相同。

目前，國內航空發動機減速器漸開線圓柱齒輪承載能力計算較多采用HB、GB、ISO、AGMA四種計算標準，其中GB方法等效采用ISO方法。近年，文獻[1]～[4]對ISO與AGMA標準的計算公式、修正系數含義、計算結果等方面作了比較和分析。通過比較，ISO標準比AGMA標準考慮的影響因素更全面，引入的修正系數更多，計算公式較復雜，兩種標準對理論推導、試驗數據和經驗公式的偏重有所不同。但現行HB(HB/Z 84.1～3-84)頒布時間較早，ISO現行版本為ISO 6336-1～6336-3:2019，最新版標準相比1996版已多次修正，內容已有較大變化，特別是斜齒輪螺旋角系數的計算發生了顛覆性的變化[5]。

筆者重點比較分析HB/Z 84.1～3-84與ISO 6336-1～6336-3:2019標準關于航空發動機減速器漸開線圓柱齒輪承載能力計算方法的差異，結合具體實例，分析兩標準間的差異對計算應力值的影響，以期獲得適用性更好更準確的齒輪承載能力評估方法。

1 計算方法

1.1 接觸強度計算

1.1.1 計算公式比較

HB/Z 84.2-84標準中，齒面接觸疲勞強度計算的基本公式為[6]：

ISO6336-2:2019標準中，齒面接觸疲勞強度計算的基本公式為[7]：

≤σHP

≤σHP

1.1.2 修正系數含義比較

為深入明確兩標準間的差異，本文根據各修正系數的含義將其分類比較(見表1)，并結合標準內容對差異較大的修正系數開展詳細分析。

由表1可知，ISO標準相比HB標準增加修正系數Kγ、ZD、ZX、ZW。詳細對比兩標準內容，關于修正系數KHβ、KHα、ZB、ZD、Zβ、ZN、ZR的估算方法上存在不同程度的差異，同時本文結合航空發動機減速器結構特點，對各系數的計算或選用給出了具體的使用建議。

表1 接觸強度計算的修正系數含義比較

ISO標準中均載系數Kγ為考慮多路徑傳動中各嚙合副載荷分配不均勻影響的系數。對于航空發動機減速器，較多采用星形/行星傳動或多路功率分流傳動，因此應合理選取Kγ對接觸強度計算結果予以修正。

ISO標準中尺寸系數ZX通常取1，齒面工作硬化系數ZW主要是考慮結構鋼、調制鋼等材料的大齒輪與光滑的硬齒面小齒輪相嚙合產生的工作硬化現象對齒面接觸疲勞強度的影響，對于航空齒輪，齒面通常會滲碳或滲氮進行表面硬化，因此ZW通常取1。

系數KHβ、KHα的估算考慮的影響因素較多，如齒輪加工精度、配對齒輪旋轉軸線的平行度、齒輪傳動系統的彈性變形、由工作溫度引起的熱變形、跑合效果、齒面修形效果等，ISO標準比HB標準考慮的影響因素更多，算法也更復雜。系數的確定應結合具體的傳動系統設計結構分析確定，文獻[8]認為，為了保證齒輪傳動的可靠性，KHβ最小值不能小于1.15。

系數ZB為齒輪節點處的接觸應力換算為小齒輪單對齒嚙合區下界點B處接觸應力的系數，ZD為齒輪節點處的接觸應力換算為大齒輪單對齒嚙合區下界點D處接觸應力的系數。HB標準中通常取節點處接觸應力作為計算依據，ZB取值為1。而在ISO標準中，對于內嚙合，ZD取為1；對于外嚙合，航空發動機減速器各級傳動比一般大于1.5，此時ZD取為1，ZB的取值則依據齒輪端面重合度εα和軸向重合度εβ計算值分情況計算。

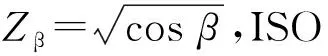
修正系數ZN的選用差異較小，對于航空齒輪來說，齒輪壽命通常按無限壽命設計，且齒輪加工精度較高，潤滑良好，因此ZN取值通常為1。

壽命系數ZR的計算公式差異較大，HB標準中ZR的計算是平均粗糙度RZ100和σHlim的相關函數，而ISO標準是關于平均峰-谷粗糙度RZ10和σHlim的相關函數。

1.2 彎曲強度計算

1.2.1 計算公式比較

HB/Z 84.3-84標準中，齒根彎曲疲勞強度計算的基本公式[9]：

σF=σF0·KA·KV·KFβ·KFα≤σFP

ISO6336-3:2019標準中，齒根彎曲疲勞強度計算的基本公式[10]：

σF=σF0·KA·Kγ·KV·KFβ·KFα≤σFP

1.2.2 修正系數含義比較

為深入明確兩標準間的差異，本文根據各修正系數的含義將其分類比較(見表2)，并結合標準內容對差異較大的修正系數開展詳細分析。

表2 彎曲強度計算的修正系數含義比較

由表2可知，ISO標準相比HB標準增加修正系數Kγ、YB、YDT。詳細對比兩標準內容，關于修正系數YF、YS、Yβ、YNT、YδrelT、YRrelT的估算方法上存在不同程度的差異，同時本文結合航空發動機減速器結構特點，對各系數的計算或選用給出了具體的使用建議。

ISO標準中均載系數Kγ為考慮多路徑傳動中各嚙合副載荷分配不均勻影響的系數。對于航空發動機減速器，較多采用行星或星形輪系，因此應合理選取Kγ對彎曲強度計算結果予以修正。

ISO標準中輪緣厚度系數YB用于薄輪緣厚度齒輪強度的評估，需根據齒輪結構設計尺寸進行計算。

ISO標準中齒高系數YDT用于修正重合度在2≤εαn<2.5、齒廓修形的高精度齒輪(ISO公差等級≤4)的齒根彎曲疲勞強度計算結果，對于航空發動機減速器齒輪，通常YDT取1。

齒形系數YF的計算，外齒輪和內齒輪的計算模型和公式不同，應分別計算。對于外齒輪，HB與ISO均以過齒廓根部左右兩過渡曲線與30°切線相切點的截面作為危險截面，但計算公式不同；對于內齒輪，HB標準為近似按齒條進行替代計算，該替代齒條在法面內具有基本齒廓的齒形，齒高與內齒輪一樣，以過齒條齒頂曲線與30°切線相切點的截面作為危險截面，ISO標準則為過齒廓根部左右兩過渡曲線與60°切線相切點的截面作為危險截面，計算模型存在本質不同。

應力修正系數YS計算公式在形式上一致，但由于YF計算過程中的部分參數計算公式的差異可導致YS計算結果的差異。

螺旋角系數Yβ是考慮斜齒輪嚙合線傾斜對彎曲強度的影響。HB中Yβ=1-εβ(β/120°)，ISO6336-3的2008版對該公式進行了修正，Yβ=(1-εβ(β/120°))*(1/cos3β)，且在以后的版本中均確認了該修改。文獻[5]就Yβ計算公式的變化對斜齒輪接觸強度的影響進行了詳細的分析，在螺旋角β=0～30°范圍內，修正前Yβ為遞減函數，修正后Yβ在β=0～9.83527°范圍內為減函數、在β=9.83527°～30°內為增函數。

修正系數YNT的選用差異較小，對于航空齒輪來說，齒輪壽命通常按無限壽命設計，且航空齒輪加工精度較高，潤滑良好，因此YNT取值通常為1。

對于修正系數YδrelT、YRrelT，ISO標準比HB標準考慮的工況更為細致全面，且有經驗公式可計算評估，而HB則通常取1。

2 算例對比

為進一步分析ISO標準與HB標準間各修正系數的差異對齒輪接觸疲勞強度和彎曲疲勞強度結果的影響，以某渦槳發動機減速器主傳動鏈為例，對其齒輪承載能力進行計算。該減速器采用兩級星形傳動，功率分三路傳遞，輪齒參數見表3，接觸強度計算結果見表4，彎曲強度計算結果見表5。

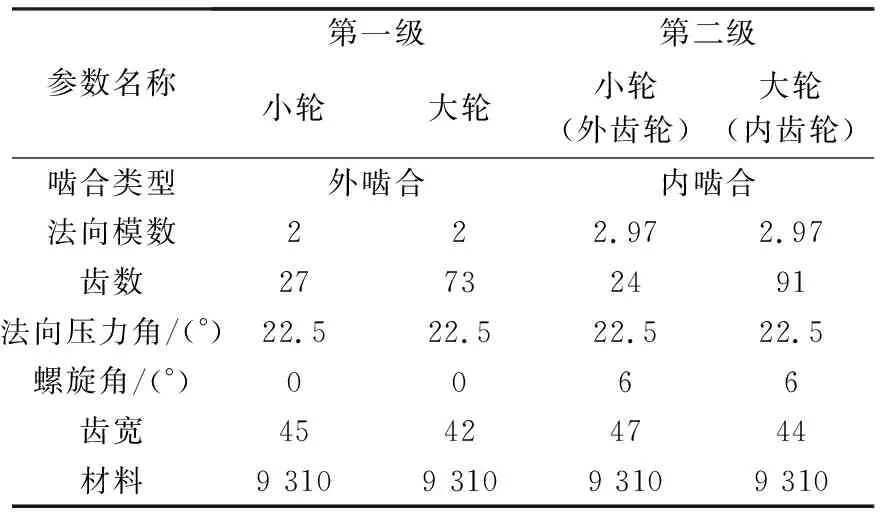
表3 輪齒參數

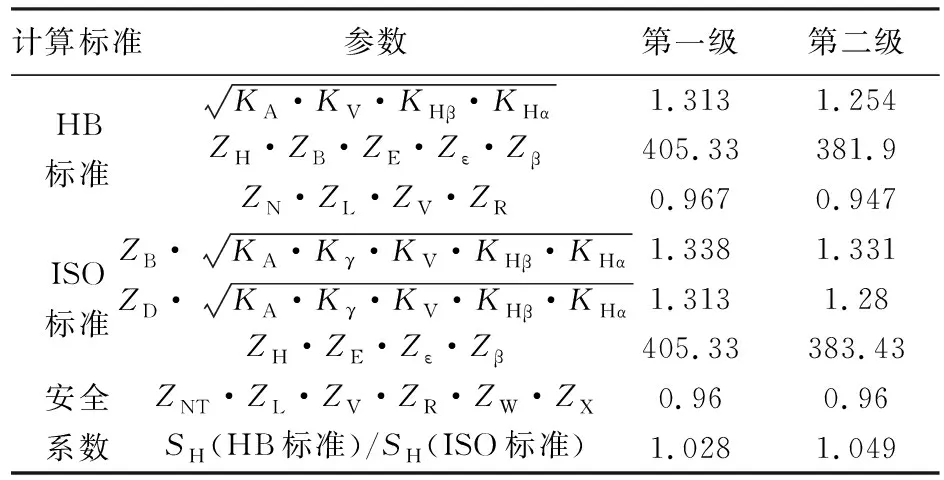
表4 接觸強度計算結果及影響分析

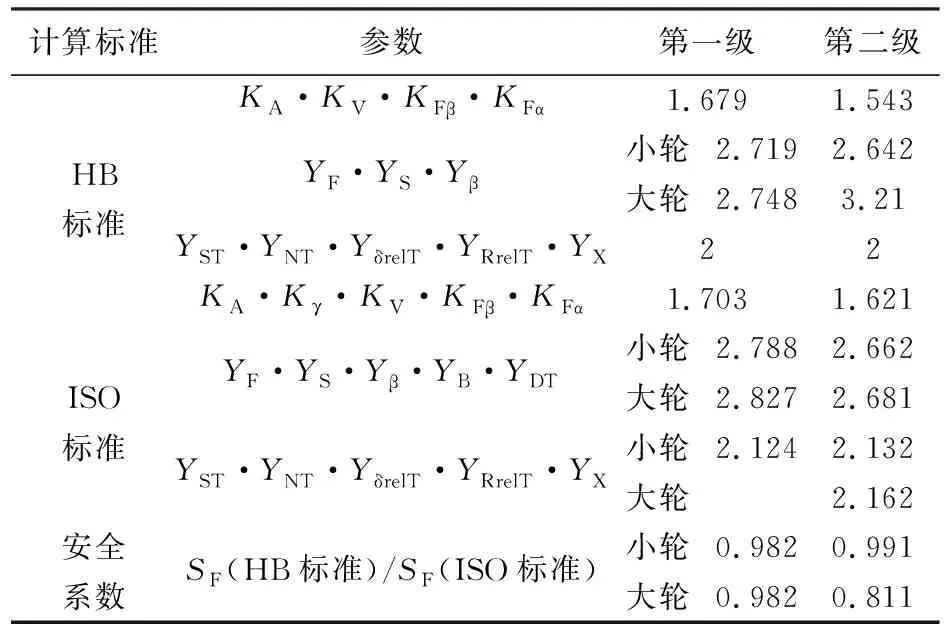
表5 彎曲強度計算結果及影響分析

由表4可知，對于外、內齒輪齒面接觸疲勞強度，HB標準計算值與ISO標準計算值差異在可接受范圍內。

由表5可知，對于外齒輪齒根彎曲疲勞強度，HB標準計算值與ISO標準計算值差異在可接受范圍內；對于內齒輪齒根彎曲疲勞強度，HB標準計算安全系數僅為ISO標準計算值的81.1%。經分析認為，造成該較大差異的主要原因為兩標準對修正系數YF的計算模型和公式存在本質不同，導致HB標準計算YF=1.255和YS=2.621，而ISO標準計算YF=0.87和YS=3.11。

3 結 論

經過詳細的計算比較和實例比較后得出：

(1) HB標準與ISO標準輪齒強度計算公式的基本理論相同，ISO標準相比HB標準考慮的影響因素更為全面。對于齒面接觸疲勞強度，ISO標準相比HB標準增加引入修正系數Kγ、ZD、ZX、ZW；對于齒根彎曲疲勞強度，ISO標準相比HB標準增加引入修正系數Kγ、YB、YDT。在航空發動機減速器應用領域，通常ZX、ZW、ZD、YDT通常取1，對結果無影響；航空發動機減速器較多采用星形/行星傳動或多路功率分流傳動，均載系數Kγ將會對結果產生較大影響；航空發動機減速器高可靠性和重量輕的特點，使得修正系數YB將會對薄輪緣齒輪的計算應力值產生一定影響。

(2) ISO標準與HB標準中螺旋角系數Zβ、Yβ的公式差異較大，文獻[5]經詳細分析認為ISO最新修訂版中Zβ、Yβ公式更具信服力，文中分析指出隨著螺旋角系數β增大，兩標準對計算應力值將產生不同程度的影響。

(3) HB中ZB取值為1，ISO中ZB的取值則依據齒輪端面重合度εα和軸向重合度εβ計算值分情況計算，此外ZR計算公式差異也較大，將對計算應力值產生影響。

(4) 齒形系數YF、應力修正系數YS是對齒根彎曲疲勞強度產生重要影響的修正系數，對于外齒輪該系數的計算，ISO標準與HB標準計算模型相同，但計算公式差異較大；對于內齒輪該系數的計算，兩標準的計算模型和公式存在本質不同，HB標準計算值較ISO標準計算值偏大。同時兩標準中YF計算值的差異間接導致了YS計算值的差異，該兩修正系數對齒輪尤其是內齒輪計算應力值產生較大影響。