基于北斗導航的路徑規劃優化算法研究
◆汪慧琳
(鄭州大學地球科學與技術學院 河南 450001)
如今,支持北斗三號系統信號的 28 納米芯片已得到廣泛應用,國內外主流芯片廠商均推出兼容北斗的通導一體化芯片,支持北斗定位的手機越來越多。通過獲取手機本身芯片提供的位置,地圖軟件就可以使用BDS進行實時定位、路徑規劃等功能。通常的地圖軟件都具備讓用戶選擇起點-終點,從而進行兩點之間最佳路徑規劃的基礎功能。現在國內的地圖軟件(高德地圖、百度地圖、騰訊地圖等)也具備設置多個途經點(主要是駕車模式)的路徑規劃,在手機端一般可以設置5個途經點(包括起點和終點),在PC端可設置途經點數較多的是高德地圖(包括起、終點共8個)。但目前仍未有一款地圖軟件,能根據用戶的預期途經點(地點數大于8)及用戶的時間期望(愿意用于出行的時間)給用戶提供智能出行規劃。一種常見的情況是:用戶在面臨需要規劃路線的情況時,容易陷入純粹的局部最優規劃(貪心算法)——總是去往離當前位置最近的位置,這往往會比真正的最優規劃多出許多里程。另一種常見的情況是:由于用戶時間有限,不能經過所有期望地點。
本文旨在通過優化智能算法得出兩種路徑規劃方式,一是讓用戶在經過所有預期途經點的條件下盡可能地減少交通里程,二是讓用戶在時間有限的條件下盡可能地減少交通時間。當基于北斗導航系統的路徑規劃能夠為用戶提出更優化的方案時,將會提升用戶體驗。
1 研究思路
首先將用戶所希望前往的地點數字化。利用北斗導航獲得每兩個地點之間的最佳駕車路徑距離,生成距離矩陣。用戶的想法分為兩類:一類是用戶期望能夠抵達所有目標地點,一類是用戶期望盡可能減少路途上的時間成本。

圖1 用戶選擇模式
2 研究內容
2.1 數據采集、處理
本文選取蘇州市25個地點為測試用例,數字及地點對應關系如下:
0-蘇州站,1-周莊古鎮,2-拙政園,3-虎丘山,4-同里古鎮,5-金雞湖,6-留園,7-寒山寺,8-千燈古鎮,9-蘇州博物館,10-獅子林,11-西山,12-盤門,13-七里山塘,14-天平山,15-甪直古鎮,16-木瀆古鎮,17-錦溪古鎮,18-東山,19-望山,20-穹窿山,21-蘇州大學,22-吳中太湖風景區,23-滄浪亭,24-網師園。
25個地點的駕車距離以矩陣形式輸入計算機。
2.2 算法優化及實驗結果分析
2.2.1n較小的情況
對于n小于13的情況,本文采用深度優先算法(DFS)實現對所有路徑的遍歷。第一類規劃問題中,對于n較大的情況,本文先后實驗了蟻群算法(ACO)、模擬退火算法(SA)。
(1)深度優先算法(DFS)
深度優先算法(DFS)流程如圖2。

圖2 DFS 算法流程
通過對該算法的優化,如建立哈希表以快速判重、減支,可以對n小于13的情況做出快速準確的處理。
(2)蟻群算法(ACO)
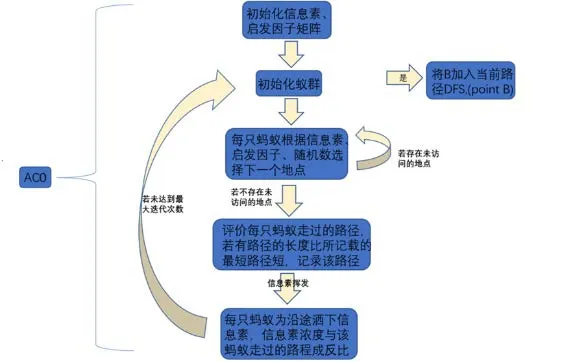
圖3 ACO 算法流程
蟻群算法中,每個地點對于其他的任意一個地點都有一個啟發值,即啟發因子,初始化值為該點與另一點距離的倒數。這表示:兩個地點之間的距離越近,啟發因子越大,因而螞蟻選擇此點的概率越大。
同樣,每個地點對于其他的任意一個地點都有一個信息素濃度,且隨著迭代(螞蟻群周而復始的運動)的進行不斷揮發、更新。其初始化值為螞蟻數量與貪心路徑(見前文中的人為選擇)長度的比值。
在t時刻,螞蟻在地點i對下一個地點j的選擇遵循以下公式:

其中表示地點i到地點j的路徑上的信息素濃度,表示地點i到地點j的路徑上的啟發值。α表示信息素參數,β表示啟發因子參數(在使用函數時可自己設定這兩個參數的值,一般取1和2)。
信息素濃度更新公式:

式(2)表示信息素的揮發;
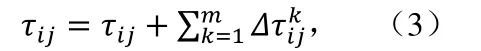
式(3)表示信息素濃度為揮發后的濃度加上螞蟻新留下的信息素濃度,每只螞蟻在兩地點間留下的新濃度為該路徑距離和的倒數。其中,m為曾從地點i抵達了地點j的螞蟻的數量,k為對應的路徑標記。
最后再設置迭代次數,算法即可開始運行。
蟻群算法的一個特性是:搜索結果收斂快,且當收斂完成時,很難再找到一條其他的路徑。當所有螞蟻都在同一條路徑上行走時,即使有螞蟻“突發奇想”向更優秀的路徑邁出了一步,也只能留下濃度不高的信息素,而由于其他螞蟻匯集于同一條路徑,導致那條路徑上的信息素濃度會很高。因此,蟻群的下一次出動中,很少有螞蟻能夠響應那位“突發奇想”的螞蟻先驅的號召,它們仍更傾向于往信息素濃度特別高的路徑上行走,故而當結果收斂于局部最優解以后,很難再迭代出一條更好的路徑。
實驗表明:迭代次數達到了50以后,再增加迭代次數也難以得到更好的結果。這樣的一個優點是:減少了計算機的算力。當導航軟件的服務器需要為所有用戶提供云計算功能時,蟻群算法的易收斂性是它的一個重要優點:對于每個用戶的路徑規劃,僅需要少量的計算機算力。
在實際測試中,選取了蘇州的13個地點(其中包含蘇州站,路徑起點和終點都為蘇州站)。首先用DFS的傳統搜索算法得到最優結果(耗時38秒)為:規劃路徑是0-3-7-6-12-11-4-1-8-5-2-10-9,路徑長度是242.8km。單獨運行5次蟻群算法得到結果如表1:

表1 經過13 個點的運行結果(單獨運行5 次蟻群算法)
算得平均路徑長度為La=(248.9+247.5+247.5+250.9+247.5)/5=248.46。而人為選擇(貪心算法)中選擇的路徑為:規劃路徑是0-9-10-2-6-7-3-12-5-4-1-8-11,路徑長度為270.2km。
定義優化程度:優化程度=100%*(貪心路徑長度-規劃路徑長度)/(貪心路徑長度)。由以上數據可知,此時傳統搜索算法優化程度為10.14%,蟻群算法平均優化程度為8.05%,蟻群算法最佳優化程度為8.40%。由8.4/10.14=82.84%知,蟻群算法5次運行可達到完美優化的82.84%,算法性能在可接受范圍內。又如前文所提,蟻群算法無須太多迭代次數,運行較快,故可在對運行速度有嚴格要求時采用蟻群算法。
(3)模擬退火算法(SA)
模擬退火算法(SA)流程如圖4。

圖4 SA 算法流程
本文采用貪心路徑作為初始化的路徑(因為貪心路徑具備一些優良特性)。在評價一條新路徑時,令Δt=length(T’)-length(T),其中T’為產生的新解(路徑),T為舊解。易知,當Δt<0時,新解較為優秀,此時用新解替換路徑。當Δt>0時,以概率exp(-Δt/T)用新解替換路徑。其中T為該時刻的溫度。
通過概率exp(-Δt/T)(其中Δt>0)可知,當T較大時,exp(-Δt/T)較大,即此時更容易發生交換,算法的全局搜索性更強;當T較小時,exp(-Δt/T)較小,算法的全局搜索性較小,趨于穩定,可以認為此時算法在優解的附近尋找更優秀的解。
降溫時根據降溫系數降溫,本文取T(t+1)=0.99997*T(t);單獨運行5 次模擬退火算法得到結果如表2:

表2 經過13 個點的運行結果(單獨運行5 次模擬退火算法)
算得平均路徑長度為La=(242.8+246.5+242.8+243.2+245.5)/5=244.16。由以上數據可知,此時傳統搜索算法優化程度為10.14%,模擬退火算法平均優化程度為9.64%,模擬退火算法最佳優化程度為10.14%。
由10.14/10.14=100%知,這5次運行模擬退火算法最好結果可達到完美優化的100%,是性能非常好的算法。由于蟻群算法僅為多用戶使用時服務器的后臺算法提供參考,而模擬退火在運行時間遠低于傳統搜索的時間的同時優化性能比蟻群算法好,且本文所述功能無須為多用戶同時提供算力,故本文后續內容基于模擬退火算法。
綜上,當點數為13時得到表3。
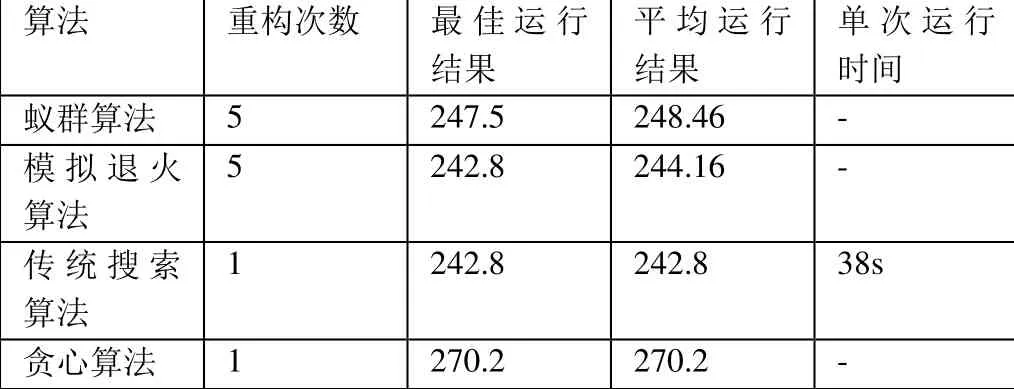
表3 四類算法性能表(13 個點)
2.2.2n較大的情況
當n擴大至25時,此時已無法使用傳統搜索算法。模擬退火算法5次運行結果如下:

表5 經過25 個點的運行結果(單獨運行5 次模擬退火算法)
而貪心路徑及長度為:規劃路徑是0-9-10-2-24-23-12-6-13-7-3-21-5-16-14-20-22-19-4-1-17-15-8-11-18,路徑長度是424.1km。算得平均路徑長度為La=(309.6+311.1+315.7+314.5+306.5)/5=311.48。
由以上數據可知,此時模擬退火算法平均優化程度為26.56%,模擬退火算法最佳優化程度為27.73%,算法性能相當出色。綜上,當點數為25時得到表6。

表6 四類算法性能表(25 個點)
許多情況下,用戶傾向于控制路途上的時間成本,使得總里程不變的情況下盡可能經過更多的目標地點。例如,一位用戶的汽車所剩汽油只夠該用戶繼續行駛100km,該用戶有多個目標地點且希望最終能回到出發點;同時用戶希望在這種情況下,所經過的點越多越好。本文研究的第二個功能便是為了解決此類問題而設計。
3 總結
本文主要論述了基于北斗導航系統的路徑規劃優化算法實現,針對用戶出行常見的兩類規劃問題,以蘇州市25個地點為實驗數據,研究了多種路徑規劃智能算法的性能,并對其進行了優化。本文通過研究提出了針對兩類情況的路徑規劃方案,且方案可視化后被證明是高效可行的,具有現實應用意義。

