單滑塊與飛輪協同姿態控制衛星運動分析
錢首元,高長生,荊武興
(哈爾濱工業大學航天學院,黑龍江哈爾濱 150001)
0 引言
從20 世紀70 年代以來,應用衛星技術迅速發展,對姿態控制系統的精度也越來越高,特別要求姿態控制系統的高精度長壽命和快速性。傳統衛星通常采用以飛輪為主的三軸姿態控制系統控制星體姿態。
傳統衛星的飛輪控制不需要消耗工質,只需要消耗電能,在衛星上太陽能電池陣的不斷補充下,不會像推力器那樣能源枯竭,適用于長時間工作。并且飛輪的精度要比噴氣控制高出一個數量級,適合于克服高軌衛星受到的周期性擾動,不會對光學儀器造成污染。但是由于飛輪存在飽和、控制力矩比較小等特點,無法實現快速的姿態機動[1]。傳統的變質心控制技術是通過調整飛行器內部活動體與載體的相對位置,使得系統質心發生變化,改變氣動力臂,從而打破原有的力矩平衡,實現對飛行器姿態的控制。變質心控制技術的優點是執行機構位于飛行器內部[2-3]。在地球中高軌道上,衛星受到氣動力和氣動力矩極小,變質心機構通過滑塊的滑動所產生的對載體的反作用力和反作用力矩改變星體的姿態,因而有著很快的響應速度。目前,陸正亮等[4-7]研究了低軌衛星利用受到的氣動力及氣動力矩配平攻角的變質心控制問題。埃及曼蘇拉大學數學系的GOHAR 等[8-11]著重研究了三軸穩定衛星的變質心姿態控制,并用李亞普諾夫方法證明了這種動力學模型的漸近穩定性。但是由于滑塊移動距離精度有限以及衛星本體慣性張量測定精度限制,變質心機構也存在控制精度低等缺點[12]。
上述文獻中還沒有針對滑塊與飛輪的協同控制衛星姿態的研究。本文在中高軌道衛星需要大角度快速機動的情況下,采用飛輪控制機構與變質心滑塊控制機構協同控制的方法,首先針對包含單滑塊與3 個飛輪在內的7 自由度衛星建立了完整的剛體動力學方程,并分析了其運動特性和動力學系統的特點;其次根據姿態指令機動角度采用最小二乘法,反向求解出滑塊需要運動的距離,滑塊執行機構跟蹤星載計算機里預先規劃存儲好的正弦運動方式運動到指定位置,這為控制器根據姿態機動指令計算出滑塊需求運動距離提供了一種工程上可行的方法;最后飛輪執行機構開始工作,使得衛星高精度地對指定角度定向。
這種聯合控制的方法,結合了衛星在變質心控制大角度機動下的快速響應與飛輪控制高精度定向等優點,能夠很好地完成中高軌衛星的快速響應機動的任務。
最后對比變質心機構與飛輪的協同控制的效果與單獨采用飛輪控制的效果,突出了兩者協同控制的優越性。仿真結果表明,單滑塊變質心衛星在衛星姿態機動過程中能快速響應。這也為單滑塊變質心衛星設想提供了一些理論參考。
1 動力學模型
1.1 系統動力學模型
單滑塊模式構型的飛行器由正方體形狀的衛星本體和位于星體內部的滑塊組成,滑塊位于系統質心正前方,由電機驅動,沿平行于削平面且垂直于本體中心線方向的滑軌內做平移運動,不可旋轉。滑塊相對本體的運動通過反作用力使得本體姿態發生變化。
本文的研究對象如圖1 所示,s、b、p 分別為系統、本體、滑塊的質心。滑塊的質量、體積以及每個軸的轉動慣量與本體相比都較小,約為本體的1/10以下。
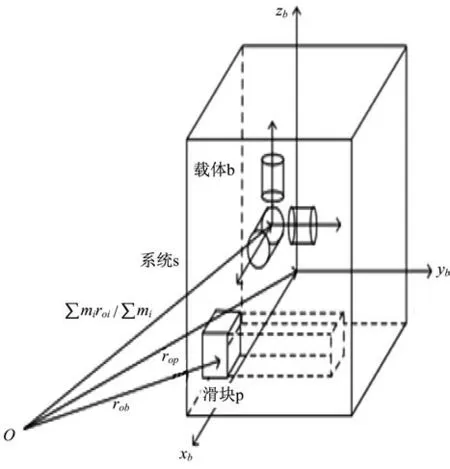
圖1 單滑塊變質心衛星示意圖Fig.1 Schematic diagram of single slider metamorphic core satellite
假設衛星在中高軌道運行,主要受重力梯度力矩等干擾力矩影響,故可以忽略氣動力和氣動力矩的影響,只考慮外部的重力梯度力矩干擾。
定義慣性坐標系(OXYZ)、系統固連坐標系(osxsyszs)和載體固連坐標系(obxbybzb),如圖1 所示。其中,系統固連坐標系的原點位于瞬時系統質心,且跟隨本體旋轉[11]。
定義變量符號,m為質量,I為慣性張量,下標s、b、p 分別為系統、載體和滑塊,rbp為從點b到點p的相對位置矢量,νb為載體相對于慣性坐標系的速度,ω為載體固連坐標系相對于慣性坐標系的旋轉角速度,g為重力。
在以系統質心為原點的載體坐標系非慣性s系中表示為
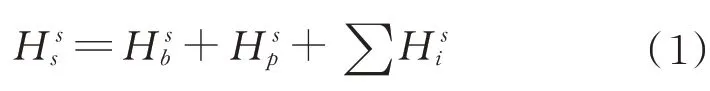
而對于衛星載體,根據相對微分法則,其角動量在非慣性s系中表示為
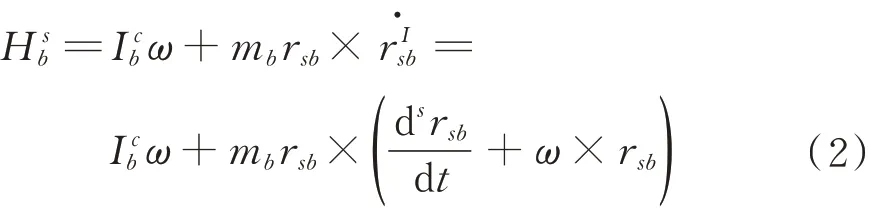
對于第i個飛輪,其角動量在非慣性s系中表示為
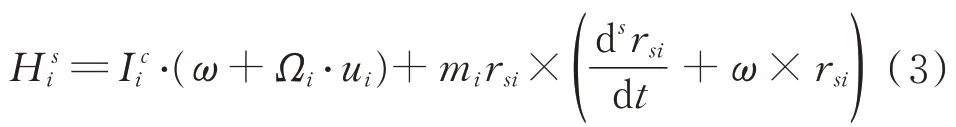
對于變質心滑塊,其角動量在本體系s系下表示為
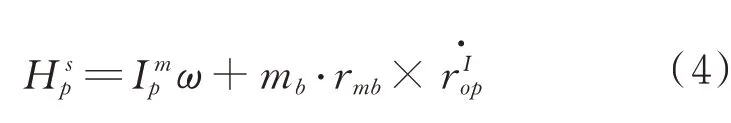
對衛星系統整體相對于系統質心s點列力矩平衡方程,并表示在本體系s系下有
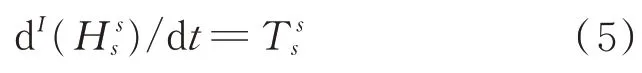
因此,根據各矢量間關系以及載體系與慣性系間的相對微分法則,載體坐標系下姿態動力學方程為
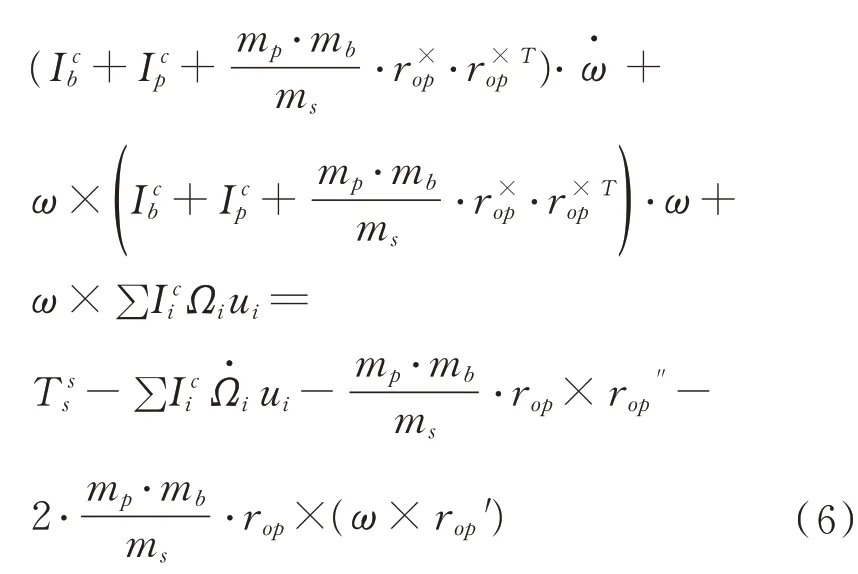
式中:(?)×、(?)′、(?)″分別為矢量在載體坐標系的叉乘矩陣、矢量在載體坐標系下對時間的一階、二階導數。
由載體動力學方程可以看出單滑塊變質心衛星具有以下特點:與傳統飛輪控制的衛星相比,飛行器載體還受到滑塊偏移產生的耦合作用力項,這些項將對載體姿態運動產生一定影響。因此,該系統是一個典型的非線性、強耦合的快時變復雜系統。
為了便于動力學分析,根據產生原因將方程右邊的附加力和附加力矩分成以下幾項:
以上各項為單滑塊變質心飛行器受到的特有的力和力矩,因此系統姿態動力學方程可以表示為
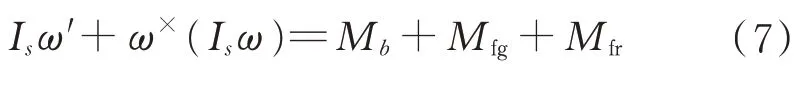
1.2 滑塊動力學模型
為了便于對直接作用在滑塊上的執行機構控制力大小進行分析,此處建立滑塊動力學方程。
由于滑塊相對載體只存在沿著滑軌的平移運動,而滑塊的質量和體積相對載體來說較小,因此可將滑塊看作質點,只用建立其質心平動動力學模型:

式中:Rop為載體滑軌約束對滑塊的作用力;Fc為載體施加的對滑塊的控制力;Gp為滑塊重力。

將式(9)在載體坐標系下代入式(8)可以得到
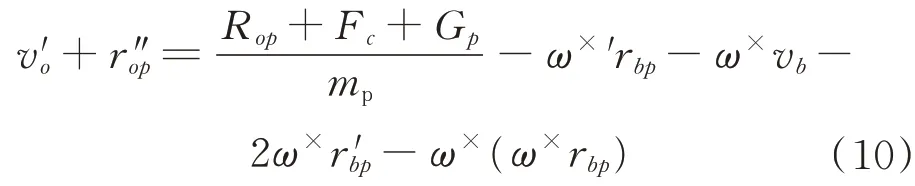
由于衛星處于整體失重狀態,忽略滑塊重力,即可得到載體坐標系下滑塊動力學方程的矢量形式:
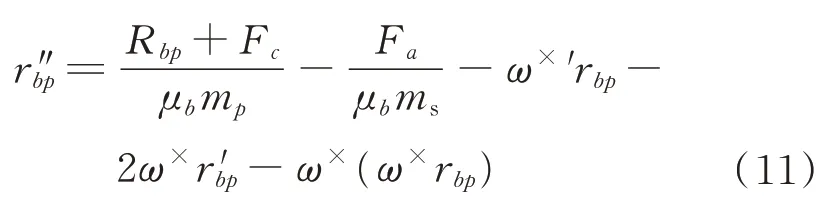
式中:方程右邊的后三項即為載體姿態運動與滑塊運動的耦合作用對滑塊運動的影響項。
1.3 滑塊需求運動距離
當衛星收到姿態機動指令,星載計算機會把姿態角指令轉化為變質心滑塊執行機構的滑塊運動距離指令,進而滑塊通過跟蹤計算機生成的正弦運動規律達到控制衛星姿態的效果。
本文采用最小二乘迭代方法把姿態角指令轉化為滑塊的運動距離指令,選取滑塊運動距離ξ為一維狀態量,建立如下殘差方程:
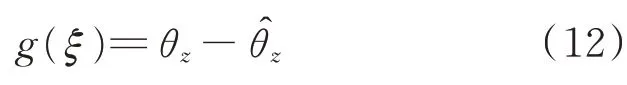
狀態量ξ的猜測誤差決定了殘差的大小,假設通過測量獲得N個采樣時刻的殘差gi(ξ),然后建立如下最小二乘指標:

依據最小二乘原理的極值條件,可以得到如下迭代估計算法:
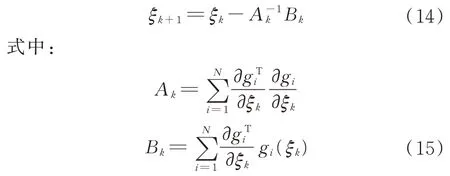
當前估計值與上一步的差的范數滿足一定精度時就停止迭代。一般經過10~20 次的迭代即可停止,則當前的估計值ξ*即為得到的精確結果。
2 飛輪與滑塊的控制律設計
2.1 飛輪控制律設計
當衛星的飛輪執行機構來控制衛星姿態的時候,利用分配矩陣與安裝矩陣實現控制力矩的分配,設計帶有補償的PD 控制率在本體系下的表示為
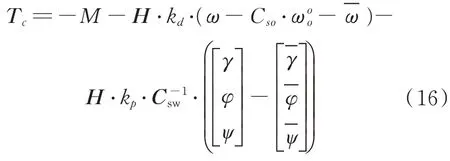
式中:H為整星系統慣性張量,即瞬時的;M為力矩合;Csw為軌道系到本體質心系的坐標轉換矩陣。
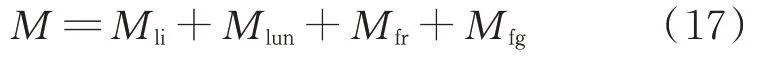
離心慣性力矩為
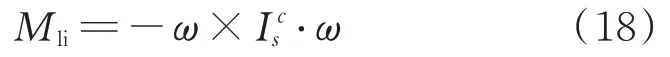
飛輪系離心慣性力矩為
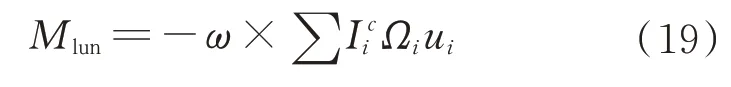
滑塊運動產生的附加相對慣性力矩為
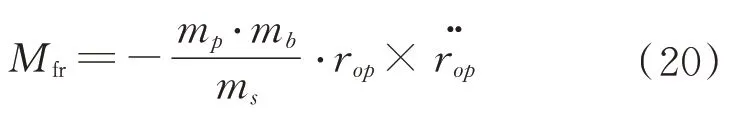
滑塊運動產生的附加哥氏慣性力矩為

根據1.1 節系統動力學方程,把飛輪對應的控制率代入式(7),可以約去補償的耦合力矩[13-16],得到
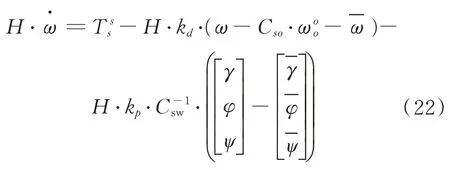
把各慣性力耦合項消掉后,減弱了僅有飛輪控制時姿態三通道的耦合效應,使得加入耦合補償控制后的方程更簡潔且更接近于對慣性環節的控制。
2.2 滑塊控制律設計
在1.3 節已經利用最小二乘迭代法設計好了滑塊的運動距離,滑塊的控制器只需把設計好的運動距離作為標稱值輸入來跟蹤上。假設滑塊采用最簡單的PD 控制率:
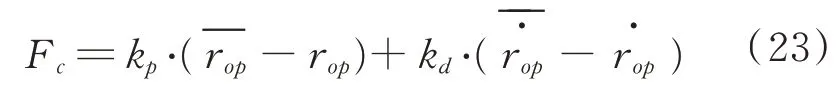
由于相對于小質量的滑塊,執行機構的控制力很大,只要合理地設計控制參數,就可以使得滑塊精確地跟蹤設計好的位置時間曲線。在滑塊滑行末端,還會有鎖死機構將滑塊鎖死,所以不存在最后的振蕩。
3 仿真校驗
本文仿真中,為簡化問題,突出現象,只考慮繞主軸Z軸轉動,其他方向的轉動可以轉換為多次繞主軸的轉動組合得到。
為使得滑塊的滑動對其他軸的姿態影響最小,本文仿真中假設滑軌設計在z=0 平面上。這樣滑塊滑動僅改變Z軸姿態,對其他兩軸沒有影響。滑塊的質量、體積以及轉動慣量與本體相比較小,設計為本體的1/10 左右,且只考慮外部的重力梯度力矩干擾。
3.1 僅飛輪控制衛星姿態
當衛星只采用飛輪控制姿態,衛星姿態機動指令為繞著Z軸轉過?5°時,仿真結果如圖2 所示。根據圖中仿真結果可知,由于飛輪的作用力矩比較小,并且存在飽和的現象,所以在飛輪的作用下,衛星姿態機動?5°需要130 s 的時間,衛星的響應時間遠長于變質心控制。
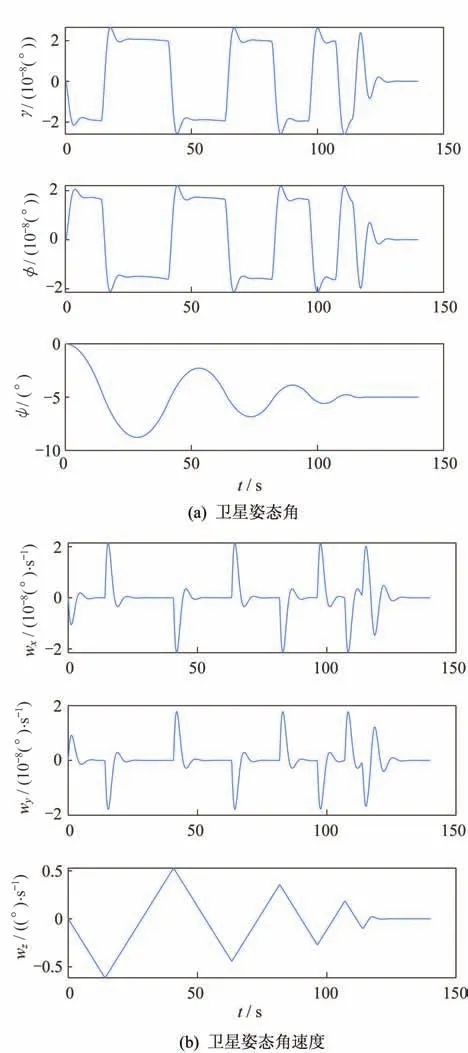
圖2 僅飛輪控制時衛星狀態量變化圖Fig.2 Variations of satellite state variables under flywheel control only
3.2 滑塊與飛輪協同控制衛星姿態
當采用文中敘述的協同控制時,首先要用最小二乘法反解求得衛星姿態繞著Z軸轉過?5°時,滑塊需要的運動距離;然后滑塊執行機構跟蹤星載計算機里預先規劃存儲好的正弦運動方式運動到指定位置,飛輪執行機構開始工作,使得衛星高精度地對指定角度定向、仿真結果如圖3 和圖4 所示。
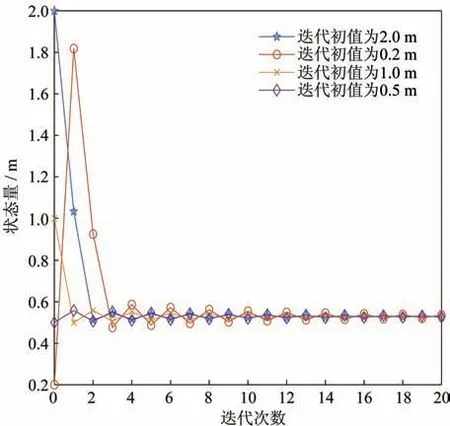
圖3 滑塊狀態量最小二乘迭代變化圖Fig.3 Variations of slider state variables under least squares iterations
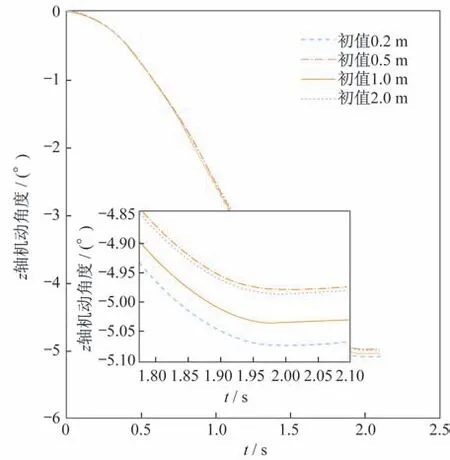
圖4 滑塊狀態的迭代結果引起的衛星姿態角變化圖Fig.4 Variations of satellite attitude angle due to slider state iterations
代入不同初值,迭代收斂的效果并不一樣。在迭代初值更接近真值的時候,迭代收斂效果最好,最終衛星轉過的角度更接近于繞著Z軸轉?5°。
根據圖中結果,選代效果最好的初值,求得為使衛星姿態繞著Z軸轉?5°,滑塊需求的運動為正向運行0.526 2 m。滑塊據此以正弦規律運行到需求位置,得出的衛星在變質心滑塊與飛輪姿態聯合控制的作用下,仿真結果如圖5 所示。
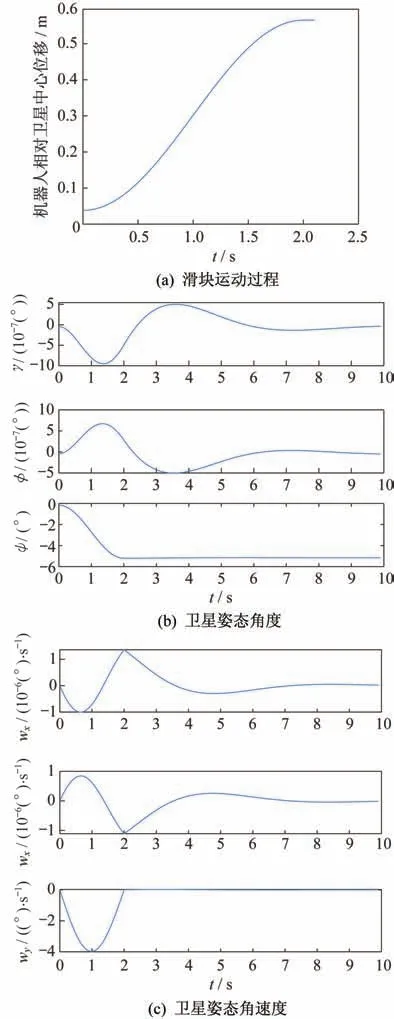
圖5 僅滑塊控制時衛星狀態量變化圖Fig.5 Variations of satellite state variables under slider control only
從仿真結果可以看出,前2 s 滑塊作用,衛星能快速機動到達期望角度附近。但是由于滑塊位移精度以及飛輪角動量的存在,使得繞著Z軸的轉動同時對其他兩軸也存在擾動,衛星三軸間存在姿態耦合,所以變質心的控制精度并不高。從2 s 到8 s,飛輪作用,衛星高精度姿態定向,并且整個機動過程僅用時8 s,要遠優于僅用飛輪單獨作用的130 s。
3.3 一種圓弧滑軌型單滑塊控制機構的可行性
由于衛星空間有限,無法實現長距離滑塊滑動,可以考慮把沿著直線滑動的滑塊改成沿著圓弧軌道滑動,設計為如圖6 所示的結構。當采用新型結構時,衛星能快速機動更大的角度。
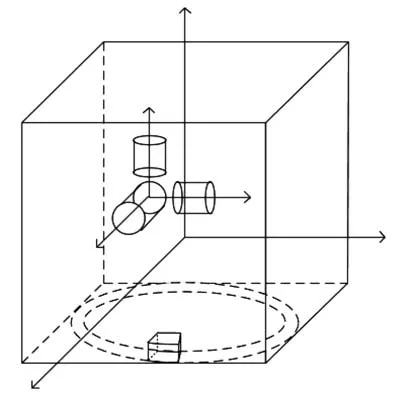
圖6 圓弧滑軌型單滑塊變質心衛星示意圖Fig.6 Schematic diagram of circular orbit type single slider metamorphic center satellite
當采用單滑塊變質心與飛輪聯合控制時,衛星機動指令為繞Z軸轉過?22°,得到的仿真結果如圖7 所示。從仿真結果可知:前16 s 滑塊運動,衛星快速繞著Z軸轉動到?22°附近;隨后在16~25 s,飛輪作用使得衛星姿態高精度定向。衛星最終穩定高精度定向時僅用時25 s。
而同樣的衛星姿態機動指令為繞著Z軸轉過?22°時,只采用飛輪控制衛星姿態,得到結果如圖8 所示。從仿真結果中可以看出,僅采用飛輪控制時,衛星要460 s 才能穩定到Z軸的?22°,所用時間比較長,消耗能量較多。
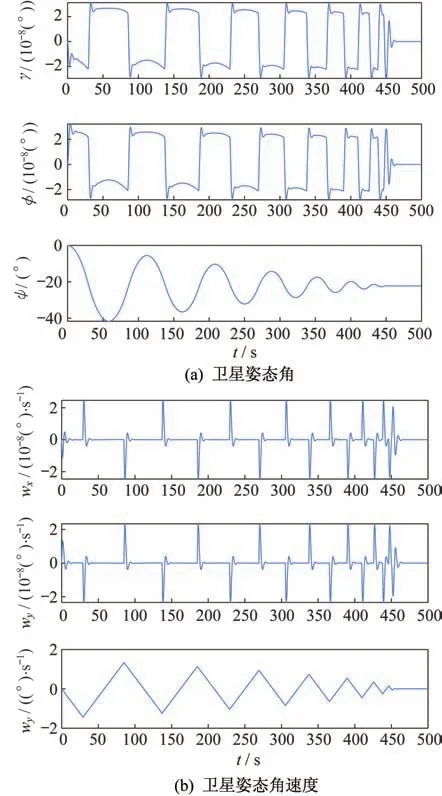
圖8 僅飛輪控制時衛星狀態量變化圖Fig.8 Variations of satellite state variables under flywheel control only
仿真結果再次驗證了當用單滑塊變質心與飛輪聯合控制僅用25 s 實現姿態機動,而僅用飛輪控制則需要460 s,遠遠長于單滑塊變質心與飛輪的聯合控制。仿真結果同時驗證了新構型的可行性,在沒有降低變質心機動效率的前提下,極大地節省了衛星載體內部的空間和滑塊質量與體積,使得這種聯合控制方案的可行性進一步提升。
4 結束語
本文的仿真結果再一次驗證了傳統衛星的飛輪控制星體姿態。由于飛輪存在飽和、控制力矩比較小等特點,無法實現快速的姿態機動。變質心控制機構通過滑塊的滑動所產生的對載體的反作用力和力矩來改變星體的姿態,有著很快的響應速度。本文采用飛輪與變質心滑塊機構協同控制的方法,提出并驗證了一種圓弧滑軌型單滑塊控制機構的可行性。這種方法結合了變質心控制快速響應與飛輪控制高精度等優點,克服了變質心機構存在的控制精度差等缺點。

