融合空間信息的交通流構造方法
范金斌,蔣云良,張雄濤
(1.浙江師范大學 數學與計算機科學學院,浙江 金華 321000;2.湖州師范學院 信息工程學院,浙江 湖州 313000)
在智能交通系統中[1],交通流量預測問題是根據歷史交通流量數據、訓練模型,并由模型來預測交通流量數值的.當前解決交通流量預測問題的模型采用的是一種深度學習方法,分別設計獲取時序特征的神經網絡模塊和空間特征的神經網絡模型,最后給出交通流量預測結果.Yu等較早提出將深度神經網絡模型用于預測交通流量,分別采用時序卷積網絡和圖卷積網絡獲取時序特征及空間特征[2];Li等結合擴散過程和時序網絡有效處理時空數據[3];Zheng等提出了深度網絡模型[4];Guo等提出采用深度網絡模型設計兩個獨立的神經網絡模塊,以分別獲取時序特征和空間特征[5];2020年,Huang等提出采用深度結構方法從分離的時序信息和空間信息中獲取時空特征,以完成交通流量預測問題[6].雖然越來越多的研究從模型設計角度提高了交通流量預測的準確性,但鮮有研究從數據預處理角度來處理具有復雜時空關系的交通數據[7].
1 相關符號與構造方法的意義
1.1 符號與基本操作
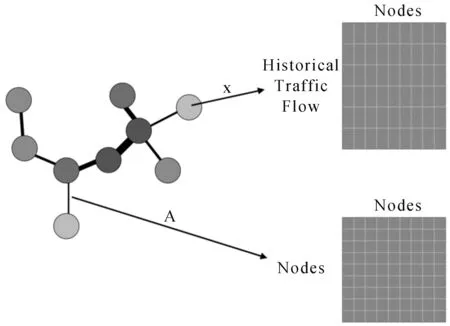
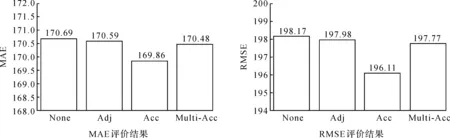
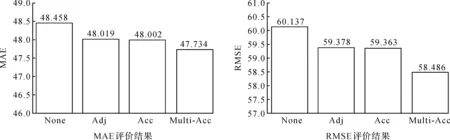
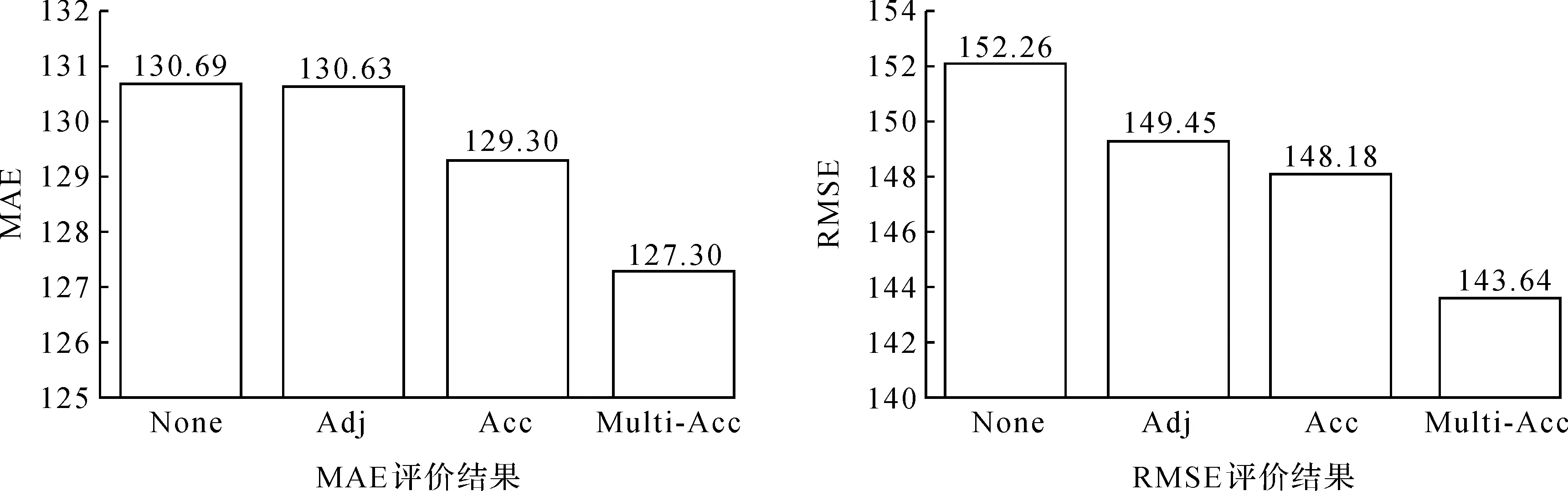
本文需要將路網建模為如圖1所示的拓撲圖G,其中,監測點作為拓撲圖上的結點,監測點間的聯系作為拓撲圖上的連邊.所構建的拓撲圖各個頂點的特征x,由包含h個時刻的一段交通流量表示.拓撲圖上各結點間的連接關系采用鄰接矩陣A表示[2].基于此,h個時刻后的可達矩陣可表示為Ah;t(1 表1 主要符號和算符 圖1 拓撲圖、圖上結點特征以及圖上鄰接矩陣Fig.1 Graph, features of nodes over graph, adjacency matrix 現有的交通流量預測方法均需從時空特征提取角度構建模型,因此需要設計大量的能獲取時序特征和空間特征的網絡模塊.但設計網絡模塊往往需要大量的時間和精力,需要在真實場景下反復驗證網絡模型的有效性、可用性等.此外,采用不同的網絡模塊雖能獲取時序特征和空間特征,但所獲取的時空狀態存在偏差[8].基于此,本文在保留交通流量時序信息的情況下,融合交通場景下的空間信息,構造兼具時空信息的交通流量數據集.采用此方法構造的數據集不但有助于簡化模型設計過程,而且有利于同時獲取時空特征,從而借助更準確的時空特征解決交通問題.在交通流量預測問題上,本文采用傳統機器學習方法對所提出的構造方法進行驗證.由實驗結果可知,結合空間信息,尤其是在多個時空下的空間信息,可有效提升交通流量預測效果. 為構造同時具有時序信息和空間信息的交通流量數據集合,本文提出兩種融合空間信息的數據集構造方法:一種是基于h跳的可達矩陣和h段的歷史觀測數據,采用圖傅立葉變換得到包含時空信息的交通流量數據;另一種是對每一時刻的可達矩陣和當前時刻的歷史觀測數據執行圖傅立葉變換,得到更準確的時空信息,從而構造具有h段的交通流量數據. 基于h跳可達矩陣構造具有融合空間信息的交通流量數據(Datasets with Acc).該構造方式中的可達矩陣結合了真實場景下的交通流量移動方式,并采用如下方式獲取每一跳的可達權重: Ah=exp(-h)·Ah-1A, (1) 其中,衰減因子h采用跳躍步長表示,即跳躍步長越大,兩個結點間所分配的權重越小.衰減過程可以很好地反映交通流量在各節點間的流動情況. 在獲得h跳可達矩陣Ah后,結合包含時序信息的交通流量數據x對拓撲圖網絡執行圖傅立葉變換,獲得包含時空信息的交通流數據集.基于可達矩陣Ah,可通過如下方式獲取拉普拉斯矩陣L: L=I-D-1/2AhD-1/2, (2) 其中,D為對角度矩陣,即對角元素對應的Ah的每行求和,非對角元素為零.再對拉普拉斯矩陣進行特征分解,得: L=UΛUT, (3) 其中:U為傅立葉空間中的特征矩陣;Λ為相應的特征值矩陣.拓撲圖上的圖傅立葉變換操作可采用如下方式進行: (4) 表2為基于h跳可達矩陣融合空間信息的構造方式;表3為基于多個可達矩陣融合空間信息的構造方式. 表2 基于h跳可達矩陣融合空間信息的構造方式 表3 基于多個可達矩陣融合空間信息的構造方式 基于多個可達矩陣構造具有融合空間信息的交通流量數據(Datasets with Multi-Acc).為更準確地獲取不同時段上的時空信息,本文對每一時段上的拓撲數據圖進行傅立葉變換.對某一時段t上的拓撲圖利用式(1)獲取可達矩陣At;基于可達矩陣At計算得到對應的對角度矩陣、拉普拉斯矩陣,從而得到所需的傅立葉空間內的特征矩陣Ut;基于上述相同方式得到傅立葉空間中的特征矩陣Ut,對t時段下的拓撲圖進行圖傅立葉變換,并結合原始交通流量,即 (5) 本文使用加州第三區開源交通流量數據集,收集于Caltrans Performance Measurement System(PeMS)平臺.所用數據集(PeMS03)包含2018年1月份的交通流量,同時覆蓋主干道上的555個監測點.本文對PeMS03數據集采用如下不同的構造方式: (1) 僅包含時序信息的構造方式(Datasets with None),即包含歷史觀測數據x. (2) 基于鄰接矩陣融合空間信息的構造方式(Datasets with Adj),即對鄰接矩陣和歷史觀測數據x執行圖傅立葉變換得到新的樣本. (3) 基于h跳可達矩陣融合空間信息的構造方式(Datasets with Acc),即本文所提出的一種數據構造方法,其中h的選定由預測長度確定.本實驗部分是預測6個時段后的預測片段,因此h的選擇為6. (4) 基于多個可達矩陣融合空間信息的構造方式(Datasets with Multi-Acc),即本文所提出的另一種數據構造方法. 以上4種不同的數據集構造方法,將在交通流量預測問題上采用支持向量回歸(support vector regression,SVR)和梯度提升模型(gradient boosting regressor,GBR)作為訓練模型,以驗證本文所提出的數據集構造方法的有效性. 具體的模型設置和訓練過程參照如下方法: 所選用的SVR模型和GBR模型采用scikit-learn中已實現的模型,并設置默認參數,其中的SVR核函數設置為線性核函數.實現的方法是對隨機的監測點進行訓練并完成測試,具體以所選監測點60%的構造數據作為訓練樣本,剩余的構造數據作為測試樣本. 模型評估采用平均絕對誤差(mean absolute error,MAE)和均方根誤差(root mean square error,RMSE)兩個數據評價指標: (6) 本文隨機選取3個監測點,得到如表4、表5、表6中的實驗結果.總體看,包含空間信息的數據構造方法能有效提升交通流量預測的準確率;在空間信息中考慮多跳和每一跳的時序信息更有利于交通流量預測.在不同的監測點,不同的數據構造方法對未來交通流量的預測有不同影響. 表4 在監測點105號上SVR的評價結果 表5 在監測點516號上SVR的評價結果 表6 在監測點319號上SVR的評價結果 由表4可知,對監測點105號提出的兩種融合空間信息的數據構造方法,在相同的實驗條件下,能在交通流量預測問題上表現出更好的預測效果,特別是基于多個可達矩陣的數據構造方法比僅包含時序信息數據的構造方法有了顯著的提升;在該監測點上,通過單一時刻空間信息的鄰接矩陣或多個時刻空間信息的可達矩陣來實現空間信息融合,同樣優于反包含時序信息的數據構造方法,但不及基于多個可達矩陣的構造方式;在該監測點上,融合更多時刻上的空間信息更有利于模型對交通流量的準確預測. 表5中,基于h跳可達矩陣的構造方式,采用SVR模型預測監測點516號的交通流量,展示出的評價結果最好.由于監測點在空間上存在差異,因此不同的空間信息在表示空間聯系時存在差異,從而模型也會給出不同的預測結果.但融合更多時段上的空間信息仍被證明有助于模型給出準確的交通流量預測.此外,表6給出的實驗數據結果也證實了表4的結論. 除采用SVR模型驗證所提出的交通流量構造方法的有效性外,本文還采用GBR模型驗證所提出的交通流量構造方法,結果如圖2、圖3、圖4所示.由圖2可見,基于h跳可達矩陣融合空間信息的構造方式,在實驗中表現出的實驗結果最好.在監測點14號上,空間信息采用h跳可達矩陣更易表示,也便于模型更好地獲取時空特征,并給出準確的交通流量預測值.在監測點327號和140號上,模型則從本文的另一種數據構造方法中獲取更準確的時空特征,并給出更準確的未來交通流量.可見,本文提出的融合空間信息有助于解決傳統模型無法解決的交通流量預測問題. 圖2 在監測點14號上GBR的評價結果Fig.2 The evaluation results of GBR on the 14th monitor 圖3 在監測點327號上GBR的評價結果Fig.3 The evaluation results of GBR on the 327th monitor 圖4 在監測點140號上GBR的評價結果Fig.4 The evaluation results of GBR on the 140th monitor 從上述實驗結果可以看出,融合空間信息有利于傳統模型給出更準確的交通流量信息;結合多個時段上的空間信息更能表示真實場景下的空間特征,更有利于提升模型預測的準確性.因此,融合空間信息的交通流量構造方法,可直接采用傳統模型解決現有問題,簡化了模型設計過程. 本文提出了兩種融合多個時刻空間信息的數據集構造方法,即基于h跳可達矩陣融合空間信息的構造方式和基于多個可達矩陣融合空間信息的構造方式.這兩種數據構造方法融合了更多空間信息,簡化了模型設計,并可采用傳統機器學習方法,即基于所構造的數據集解決現有交通問題.此外,該數據構造方法有助于模型同時獲取時空信息. 基于已提出的數據集構造方法,我們將會在更多的模型及交通流量場景下對數據集構造方法進行優化,尤其是要通過構造鄰接矩陣來更準確地表示各監測點間的差異,從而提升該數據構造方法在整個路網上的預測效果.
1.2 融合空間信息的意義
2 融合空間信息的構造方法
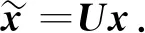


3 實驗分析
3.1 實驗設置
3.2 結果分析



4 結 語

