Kaup-Boussinesq方程的留數對稱和相互作用解

呼 星 汝

西北大學 數學學院，西安 710127

非線性演化方程及其精確解在物理、自然科學等領域有著非常重要的作用，因此構造非線性發展方程的精確解一直以來都是廣大數學物理研究的重要問題之一． 眾所周知，對稱群理論[1]和Painlevé分析理論[2-3]是發現和解決非線性演化方程的兩大重要方法． 在可積系統中，獲取非局域的方法主要有逆遞推算子法[4]、Darboux變換法[5]、B?cklund變換法[6-7]、截斷的Painlevé方法[8]等． Painlevé分析是研究系統可積性的重要方法之一，其重要的一個推廣是截斷的Painlevé展開方法． 該方法不僅可以直接構造系統的B?cklund變換和解析解，還可以用來構造系統的非局域對稱，并且很多方程的相互作用解可以由非局域對稱得到． 文獻[9]在做非局域對稱的Painlevé截斷展開時發現，奇異流形的留數是一個非局域對稱，稱為留數對稱[9]． 文獻[10]通過Painlevé截斷展開方法提出了相容的Riccati展開方法(CRE)，此方法不僅可以用來證明方程的CRE可解性，而且可以根據可解性來構造方程的不同類型的相互作用解，例如孤立子、橢圓函數解等，這說明很多可積系統是相容Rccati展開可解并具有相互作用解的．

本文主要研究了如下形式的Kaup-Boussinesq方程[11]

(1)

方程(1)描述了淺水波運動，其中u(x，t)表示水平底部以上的水面高度，v(x，t)是相關的水平速度場． 當γ=2時，方程(1)可化為Boussinesq系統

(2)

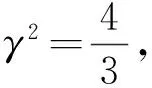
(3)

文獻[11]利用F展開法得到了方程(1)的一些精確解；文獻[12]給出了廣義Kaup-Boussinesq方程的不變解和守恒律；文獻[13]利用Euler-Lagrange變分原理得到了Kaup-Boussinesq方程的守恒律． 目前，方程(1)的留數對稱及其相互作用解還未被研究．

本文首先利用截斷的Painlevé展開方法構造了Kaup-Boussinesq方程(1)的留數對稱，并通過引入新的函數關系使之局域化；然后通過CRE方法證明了方程(1)的相容Riccati展開可解性，并利用此性質構造了方程(1)的相互作用解． 在求解的過程中，根據Riccati方程的解和橢圓方程的解，再結合Jacobi橢圓函數和第三類不完全橢圓積分構造出了一組新的橢圓周期波與孤立波相互作用解． 通過對KB方程的研究發現，CRE方法與Jacobi橢圓函數、第三類不完全橢圓積分的結合是探索非線性方程新的精確解的一種十分便捷且有效的方法．

1 留數對稱及其局域化

對于Kaup-Boussinesq方程，相應的Painlevé截斷展開式為

(4)

(5)

并且φ滿足如下的Schwarzian形式

(6)

其中

Schwarzian形式(6)在下面的M?bious變換

(7)

保持不變． 把(4)式代入方程(1)可以得到下面的定理：

定理1(自B?cklund變換定理) 如果φ滿足方程(6)，則

(8)

是方程(1)的一個解．

定理2Kaup-Boussinesq方程具有下面形式的留數對稱：

(9)

其中：u，v，φ滿足(8)式；σu，σv分別為u，v的對稱．

證方程(1)的對稱方程是

(10)

把(9)式代入(10)式中，在方程(6)和(8)的幫助下，(10)式是成立的．

為了使留數對稱非局域化，我們引入兩個新的變量

φx=fφxx=g

(11)

將Kaup-Boussinesq方程的非局域留數對稱局域化為擴展系統

(12)

的Lie點對稱

(13)

相應的Lie點對稱向量場為

(14)

最后根據Lie點對稱第一定理，解下列初值問題

(15)

得到如下的對稱群變換定理：

定理3若u，v，φ，f，g是擴展系統(12)的解，則

(16)

也是該系統的解，其中ε是任意群參數．

2 CRE可解及其相互作用解

2.1 CRE可解

通過領頭項分析，我們可以得到KB方程有如下形式的解：

(17)

式中v0，v1，u0，u1，u2是關于x和t的待定函數，R(w)是Riccati方程

Rw=a0+a1R(w)+a2R(w)2

(18)

的解，這里a0，a1，a2是任意常數． 將 (17)式和Riccati方程(18)式代入到方程組(1)中，消去R(w)的各階系數，可以得到

(19)

其中w滿足Schwarzian形式：

(20)

顯然，如果w是相容性方程(20)的解，則由R(w)和(19)式可知(17)式是方程組(1)的解．

綜上，我們得到如下定理：

定理4對于給定的方程(20)，如果w是方程(20)的解，則

(21)

是KB方程組(1)的解，其中v0和u0滿足方程(19)，R≡R(w)是Riccati方程的解．

2.2 KB系統的相互作用解

我們知道Riccati方程有如下形式的雙曲正切函數解：

(22)

(23)

由定理4可知，只要找到相容性條件(20)的解，代入到方程(23)就可以得到KB方程的解． 我們假設w具有如下特殊形式的解

w=k1x+p1t+W(k2x+p2t)，W(k2x+p2t)=W(ξ)=W

(24)

其中W1≡W1(ξ)=Wξ滿足橢圓方程：

(25)

式中Ci(i=0，…，4)是常數． 把(24)式和橢圓方程(25)式代入到相容性方程(20)中，經過計算得到：

(26)

顯然橢圓方程(25)的通解可以用雅可比橢圓函數來表示，將(25)式的解取為如下形式：

W(ξ)=cEπ(sn(ξ，m)，n，m)

(27)

其中，sn(ξ，m)為一般的橢圓正弦函數，Eπ(sn(ξ，m)，n，m)是第三類不完全橢圓積分，則

w=k1x+w1t+W(ξ)=k1x+w1t+cEπ(sn(k1x+w1t，m)，n，m)

(28)

把(28)式代入到(23)式中，即可得到方程組(1)的一組孤立波與橢圓周期波的相互作用解：

(29)

式中

S=sn(ξ，m)

C=cn(ξ，m)

D=dn(ξ，m)

取參數如下：

(30)

則KB方程的孤立波與橢圓周期波的相互作用如圖1所示．

圖1 KB方程的孤立波與橢圓周期波的相互作用示意圖

3 結束語

本文以具有物理背景的Kaup-Boussinesq方程為研究對象，運用數學軟件Maple，通過Painlevé截斷展開法得到了方程的留數對稱，并且將留數對稱局域化為擴展系統的Lie點對稱． 留數對稱的局域化過程，是求解非線性演化系統相互作用解的重要方法之一． 此外，在Riccati方程的幫助下，證明了KB方程是CRE可解的，并且給出了方程組(1)的孤立波與橢圓周期波相互作用解． 最后通過計算機模擬給出了孤立波與橢圓周期波相互作用解的圖像． 由此可知，CRE方法不僅可以構造可能存在的可積系統，而且對于構造不同類型的相互作用解是非常有效的．