趣味數學
陳新龍
楊輝三角是二項式系數在三角形中的一種幾何排列,在南宋數學家楊輝在1261年所著的《詳解九章算法》一書中出現,楊輝三角的出現是數學史上一個偉大的成就,它把二項式系數圖形化,把組合數內在的一些代數性質直觀地從圖形中體現出來,形成一個無限對稱的數字金字塔,這是一種離散型的數與形的結合(如圖1)。
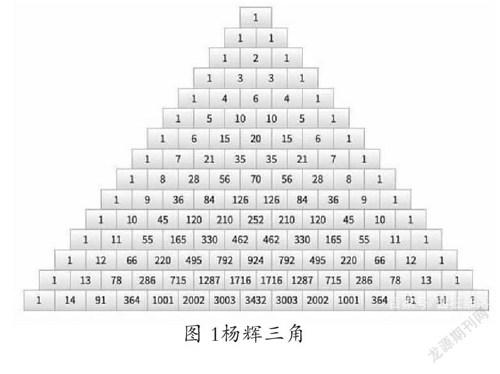
1.算法分析
那么今天就和大家一起探討一下如何用Scratch和Python繪制出楊輝三角,別看楊輝三角這么復雜,但是只要我們分析出其中的規律自然就可以克服困難(如圖2)。
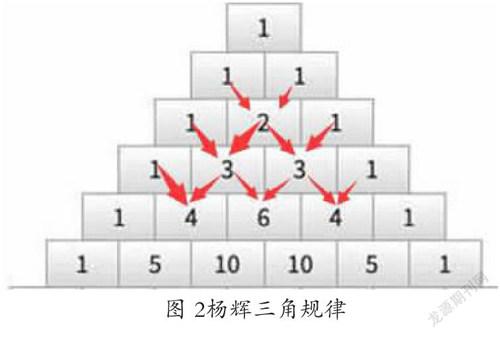
通過觀察我們發現楊輝三角的兩個腰上的數都是1,如圖2所示相加關系用箭頭標識,中間位置的數都是它頂上兩個數之和。因此楊輝三角的每行首尾數都為1,中間每個數等于它上方兩數之和,比如第二行的數為【1,1】,第三行【1,2,1】其中的數字2是第二行的數1+1之和(如圖3)。
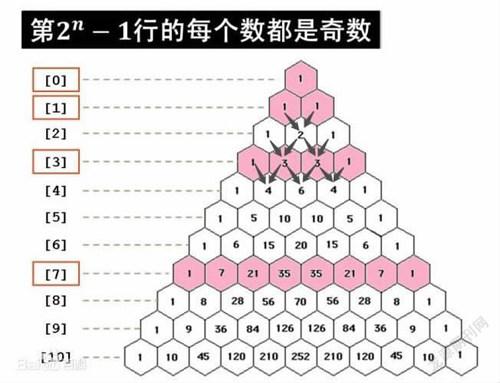
且每行數字左右對稱,由1逐漸變大,第n行的數字有n項,我們還可以總結出一個規律(a+b)nn的展開式中的各項系數依次對應楊輝三角的第(n+1)行中的每一項。
2.在Scratch中計算
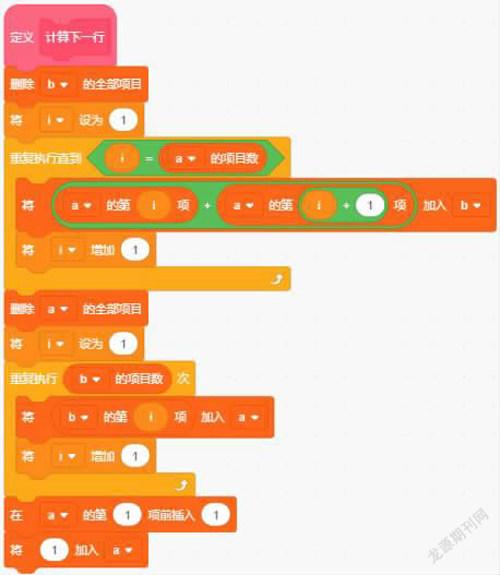
我們可以利用上一行的數據計算出楊輝三角的下一行數據,因此可以定義兩個列表,其中a列表存儲上一行的數據,b列表存儲a列表各項兩兩相加的結果,這樣就獲得了下一行的除首尾兩個1以外的數據,將b列表首尾各加1個1之后存入新的a列表獲得下一行的全部數據(如圖4)。
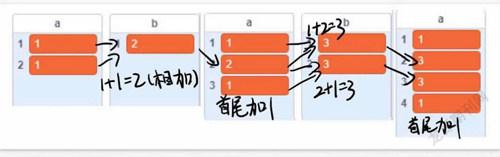
初始的情況下我們給列表a添加了兩個數字【1,1】,代表楊輝三角的第二層;1+1=2獲得列表b;給b的首位和末位加上1,就能獲得第三層的數據【1,2,1】,讓程序把a列表的數據清空,將剛剛獲得的b列表內容在首位和末位加1存儲到a里面,如此一層一層地循環到需要的層數后輸出就可以了(如圖5)。
3.在Scratch中繪制
我們通過找規律,成功將圖形轉化為了數據,解決了數據來源問題。由于Scratch不能像Python或者c語言那樣將列表中的數據直接顯示到舞臺上,所以我們得想個辦法讓數字角色根據已知數據排列成我們需要的楊輝三角。
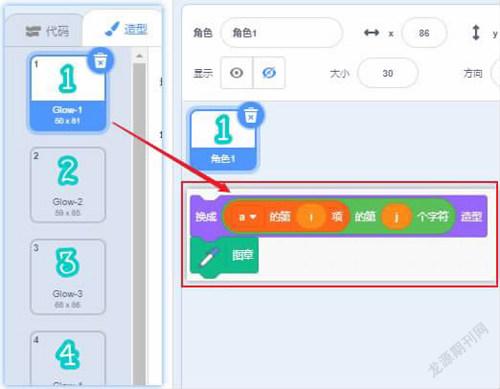
從角色庫中添加數字造型0-9,全部數字造型在一個角色中。現在我們只需要根據不同的數字切換出不同的造型,利用畫筆里的圖章將數繪制在舞臺上。還需要讓這些數字根據需要排列在合適的位置上(如圖6)。
第一行位置就定在舞臺中線正上方,下一行需要根據實際情況去測試和調整。經過測試找到了一個合適的間距,為了方便調整我使用了公式:【x:0-20(行數-1),Y:Y坐標-30】,行間距為30,數字之間的間距為30。
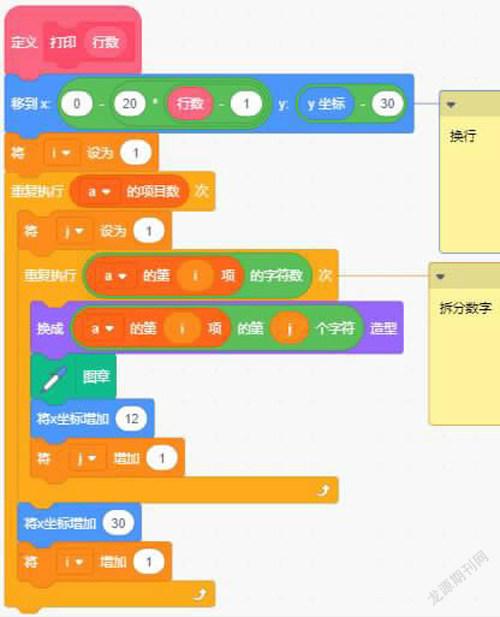
這個時候不知道你有沒有注意到一個問題,我們如果要輸出兩位數甚至三位數該怎么辦呢?比如要輸出15,但我們的角色只有0-9,這個時候我們可以使用拆分的方法,將多位數獨立拆出來。1放在前面,移動x坐標12,5放在后面,結合起來就是數字15了,用一個循環嵌套解決了輸出多位數的煩惱(如圖7)。
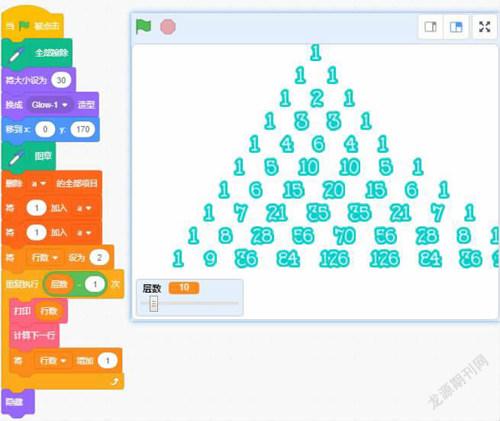
以上把用Scratch繪制楊輝三角所遇到的難題全部解決了,接下來我們可以按照整體的思路框架搭建主程序,最終可以看到我們運行后的結果了。圖中看到等腰三角形效果,由于到下層數字越來越大,占據的寬度也越來越大,所以整體會慢慢向右移動,后期我們還可以優化調整(如圖8)。
4.在Python中繪制楊輝三角
在已經分析出算法的情況下,我們再一起來思考如何用PVthon做出楊輝三角的造型。下面我會給大家展示兩種不同的做法,普通方法和進階方法兩者大家都可以嘗試。

這個方法算法與剛才Scratch的算法一致,定義dict temp變量用來存放楊輝三角中的數值,首先賦予i變量范圍range(1,11)代表行數,接下來賦予i變量范圍(0,i)代表每行的個數,第一行一個,第二行兩個……每行首尾數字都是1,中間數字等于上一行的左右兩個數字之和,即第n+l行的第i個數等于第n行的第i-1個數和第i個數之和。即dict temp(i-1,1)+dict_ternp(i-1,j-1)得出結果后我們根據dict ternp中的內容進行輸出便可以顯示出對應的楊輝三角。

創建列表nz=[1]。增加一個外循環控制行數,在循環中增加兩個條件,第一個條件是控制每行的個數,第二個條件是控制每行輸出的數字,首先我們輸出變量n,接下來給n末尾添加一個數0,通過一個循環對數進行控制n=z[n[k]+n[k 1]for k in range(i+2)]。比如第二行的內容是【1,1】,通過循環n[k]+n[k-1]等于【1,2,1】,這樣大大節約了代碼量,但是提高了代碼的認知難度。

現在代碼只是有了正確的數字,但這些數字還沒有在正確的位置上,需要你用合適數量的空格來填滿。

