基于應力判據法的拉林鐵路巖爆烈度分級

吳枋胤 ，何 川 ，汪 波 ，張鈞博 ，蒙 偉 ，劉金松

（1.西南交通大學交通隧道工程教育部重點實驗室，四川 成都 610031；2.中鐵二院工程責任有限公司，四川 成都 610031）

巖爆現象是指在高地應力地區地下工程開挖后，由于洞室圍巖的應力重分布和應力集中，巖體中積聚的彈性變形勢能突然釋放，導致圍巖爆裂、彈射的動力現象，具有很強的突發性、隨機性和危害性[1].國內外眾多巖爆研究成果和大量巖爆實際資料及試驗數據表明：發生不同等級的巖爆、巖體應力與巖石單軸抗壓強度的比值達到某一臨界值是一種基于應力強度比的判別方法.許多學者將這種判別方法用到巖爆的預測研究中[2-9]，這種方法的優勢在于：施工前可對隧道全線進行地應力反演，得到地應力場以后可以模擬開挖后的洞壁二次應力，根據地質資料可得到巖石單軸抗壓強度的大致范圍，即可在施工前對隧道全長進行一個初步的巖爆預測，給隧道的設計提供重要參考；在施工期，洞壁二次應力以及巖石單軸抗壓強度的實測數據容易獲取，可隨著隧道開挖得到小范圍的精確的巖爆預測，確保現場的安全施工.

關于巖爆的應力判據目前有多種形式，但總體上是從巖體應力及巖性條件兩方面進行考慮的，其認為地應力與巖石的抗拉或抗壓強度達到一定比值就可能發生巖爆，現有的應力判據中，大多都用洞壁切向應力 σθ及洞壁巖石單軸抗壓強度Rc的比值進行巖爆等級的劃分：挪威的Russenes 在1974 年提出了一種在國外很有影響的巖爆烈度分級方案，并應用有限元法和Kirsch 方程計算洞壁最大切向應力σθmax，繪制出巖爆烈度與洞壁 σθmax和巖樣點載荷強度值Is的關系圖，用于預報和判定巖爆等級，把Is轉換成Rc，獲得了巖爆Russenes 判據[7]；Turchaninov根據科拉半島希賓地塊的礦井建設經驗，提出巖爆活動性由洞壁切向應力 σθ和軸向應力 σL之和與Rc之比確定[10]；Hoek 等[11]總結了南非采礦巷道圍巖破壞的觀測結果，提出了對巖爆分級的判別式為 σθ/Rc=0.34（少量片幫），σθ/Rc=0.42（嚴重片幫），σθ/Rc=0.56（需重型支護），σθ/Rc=0.70（嚴重巖爆）；徐林生等[12]結合川藏公路二郎山隧道的工程實踐，對巖爆烈度分級做了系統研究，確定了各等級巖爆對應的 σθ/Rc臨界值；彭祝等[13]采用Griffith 理論對圍巖的應力狀態進行分析，以巖石抗壓強度與抗拉強度之比為參數，建立了巖爆烈度分級的判別方法；陶振宇等[14]在Barton 判據的基礎上，以Rc與巖體初始應力場的最大主應力 σ1的比值為指標，細化了巖爆發生的具體等級范圍；張津生等[15]綜合考慮了圍巖應力與應變特性，以 σθ和Rc為參數，提出了一個簡明的巖爆判據；姚寶魁等[16]認為只有當 σθ與Rc之比大于0.15 才可能發生巖爆.

上述基于應力強度判據的巖爆預測法數據可靠，易于實施，但這種判據往往是在某一條特定的隧道、某種特定地質條件的基礎下提出的，在拉林鐵路復雜的地質條件下，沒有很好地適用性，故此提出一種針對拉林鐵路的巖爆判據顯得尤為重要.本研究以拉林鐵路桑珠嶺隧道現場實測數據、現場巖爆記錄為基礎，進行巖爆判據中不同等級下臨界基準值的研究，結合kNN（k 近鄰分類）機器學習算法[17-18]提出針對拉林鐵路的巖爆判據及烈度分級，并將其用于拉林鐵路其他典型巖爆隧道（達嘎拉隧道、祝拉崗隧道、崗木拉隧道）的巖爆等級判定，與實際情況對比分析，驗證其可靠性及適用性.

1 桑珠嶺隧道巖爆發生概況及烈度分級

桑珠嶺隧道隧址區位于藏南谷地桑加段上游段，隧道最大埋深1 347 m，典型的高山峽谷地貌，先后穿越了沃卡地塹東緣斷裂F5-2和呈近南北向展布的巴玉斷層F3，是拉林鐵路全線控制性重難點工程[19]，隧道巖性以花崗巖、閃長巖等極硬巖為主，是典型的高地應力硬巖隧道，為進一步對桑珠嶺隧道的巖爆發生規律進行分析總結，課題組在施工期間對桑珠嶺隧道各洞段巖爆發生情況進行了跟蹤記錄.

1.1 巖爆破壞方式

1.1.1 薄片狀剝落

巖爆時巖石呈薄片狀松脫、剝落，厚度 ＜ 10 cm，破裂面平直，如圖1（a）所示.

1.1.2 棱板狀破裂

洞室開挖后，圍巖應力分異，發生鼓脹，在內部逐漸形成破裂面，隨著時間推移，應變能慢慢釋放，破裂面逐漸貫通，最后發生棱板狀的破裂，破裂面中間平整，邊緣處呈現梯狀，如圖1（b）所示.

圖1 巖爆破壞方式Fig.1 Rock burst failure modes

1.1.3 板狀、大塊徑爆裂

在桑珠嶺隧道極高地應力區段，洞室開挖后，圍巖局部應力高度集中，巖石發生鼓張爆裂.主要為剪切破壞，表現為大塊徑（＞ 25 cm）巖石彈射、拋射，并伴隨巖粉噴射，產生巨大的聲響，巖爆發生后會形成大直徑空腔，如圖2 所示.

圖2 巖爆后形成巨大空腔（DK183+000）Fig.2 Huge cavity formed after rockburst (DK183+000)

1.2 爆裂、崩出巖石塊徑特征

桑珠嶺隧道巖爆烈度以輕微、中等為主，少有強烈巖爆發生，根據現場巖爆記錄資料，輕微巖爆剝落的巖石塊徑多在2～10 cm，中等巖爆彈射的巖石塊徑在5～40 cm，強烈巖爆拋射、崩出的巖塊最大塊徑達到了60 cm，具體統計見表1，可見巖爆崩出的巖石塊徑與巖爆烈度等級具有正相關性.

表1 桑珠嶺隧道巖爆發生次數Tab.1 Rockburst occurrence frequency in the Sangzhuling tunnel

1.3 巖爆時效特征

桑珠嶺隧道巖爆發生一般會滯后于開挖爆破一段時間，根據等級不同，期間會發生多次掉塊、剝落甚至彈射現象，持續時間在幾秒到幾十分鐘不等，之后巖爆活動頻率降低，偶有掉塊現象發生，在DK183 +142 強烈巖爆段，第一次巖爆時具有突發性并迅速向圍巖深部擴展，在開挖后幾個月內依然會不定期發生巖爆，出現剝落、掉塊等現象.

對現場實際記錄的380 個巖爆點進行統計，得到了巖爆次數與第一次巖爆發生距開挖時間以及持續時間的關系，如表1 所示.由統計可知：桑珠嶺隧道開挖后第一次巖爆主要在開挖后3.5 h 范圍內，其中大部分集中在2.5～3.5 h 內，即開挖后3.5 h 內是巖爆發生的高峰期；第一次巖爆的持續時間集中在10 min 以內，而持續時間15 min 以上的十分少見，即在開挖后第一次巖爆開始后10 min 內巖爆活動頻繁，為巖爆危險期.

1.4 巖爆與埋深的關系

桑珠嶺隧道隧址區地面標高3 300～5 100 m，高差達1 900 m，隧道最大埋深為1 347 m，為研究桑珠嶺隧道巖爆與隧道埋深之間的關系規律，將桑珠嶺隧道按照埋深分為 ＜ 400 m、400～900 m、≥ 900 m 3 個部分，每個部分長度分別為7.5、4.6、5.0 km，統計結果見表2.

由表2 可以看出：桑珠嶺隧道巖爆主要集中在400 m 埋深以上的洞段，其中埋深400～900 m 洞段發生的巖爆占比42.09%，埋深 ≥ 900 m 洞段發生的巖爆占比41.43%，可見桑珠嶺隧道巖爆發生次數與隧道埋深之間有一定的正相關性；從巖爆等級看，在埋深 ＜ 400 m 洞段發生了6 次強烈巖爆（DK186 +167～DK186+194 段），在埋深400～900 m 洞段共發生了22 次強烈巖爆，而埋深最大的洞段一次強烈巖爆都沒有發生，可見埋深對桑珠嶺巖爆等級的影響并不敏感，這可能是因為強烈巖爆區段的構造應力較大的原因，因此并不能單從埋深來判斷桑珠嶺隧道巖爆發生的等級.

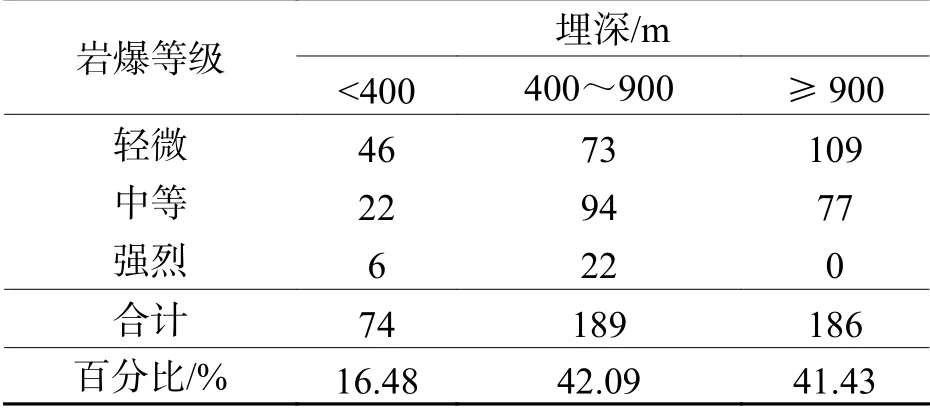
表2 桑珠嶺隧道不同埋深段巖爆統計Tab.2 Rockburst grades of different buried deep sections in the Sangzhuling tunnel 次

1.5 巖爆烈度分級方案

根據王蘭生等[20]提出RMS 方案（二郎山公路隧道圍巖巖爆分級方案）時采用的分級原則和依據，結合桑珠嶺隧道實際發生巖爆情況，提出了表3 所示的巖爆烈度分級方案.

表3 巖爆烈度分級方案及判據Tab.3 Classification scheme of rockburst intensity and rockburst criterion

桑珠嶺隧道全線各洞段在施工期間均發生了不同程度的巖爆，根據一號橫洞、二號橫洞、三號斜井及出口洞段現場巖爆的實際記錄，從聲響特征、運動特征、坑深以及形態特征方面參照桑珠嶺巖爆烈度分級方案對實際發生的巖爆進行等級判定，這對于應力判據的提出十分關鍵，桑珠嶺隧道全線實際發生巖爆等級判定結果如圖3 所示.

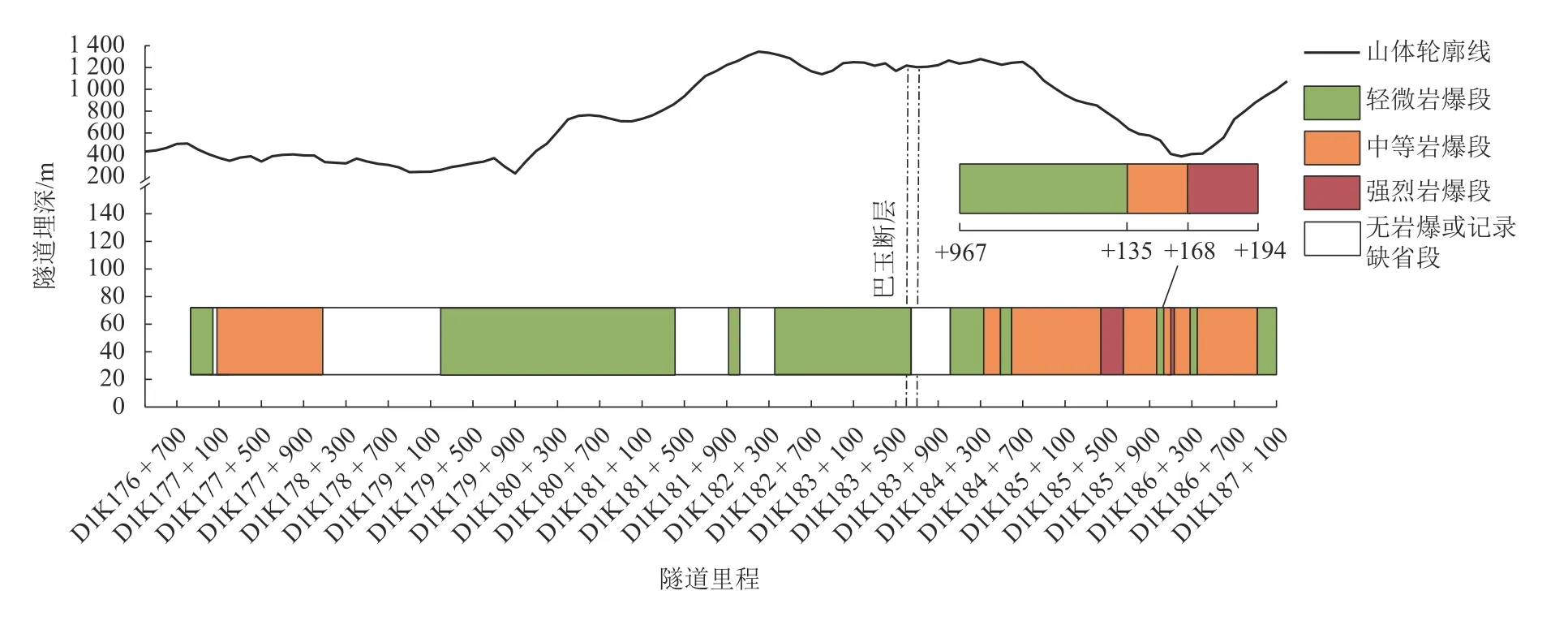
圖3 實際巖爆判定Fig.3 Actual rockburst judgement

2 拉林鐵路各級巖爆烈度標準值研究

桑珠嶺隧道全線巖體完整性好、強度高，因此可認為隧道開挖后局部洞壁巖體為均質各向同性彈性體，故可采用表面應力解除法測量隧道開挖后的洞壁二次應力分量，如圖4 所示，運用此方法測得了隧道全線洞壁二次應力實測值，并基于此對全線進行了應力場的二次修正[21]，圖中：θ1為平面內任一角度；ε1為測量平面內角度為θ1方向上的應變值；ε0為0° 方向上的應變值；ε45為45° 方向上的應變值；ε90為90° 方向上的應變值.

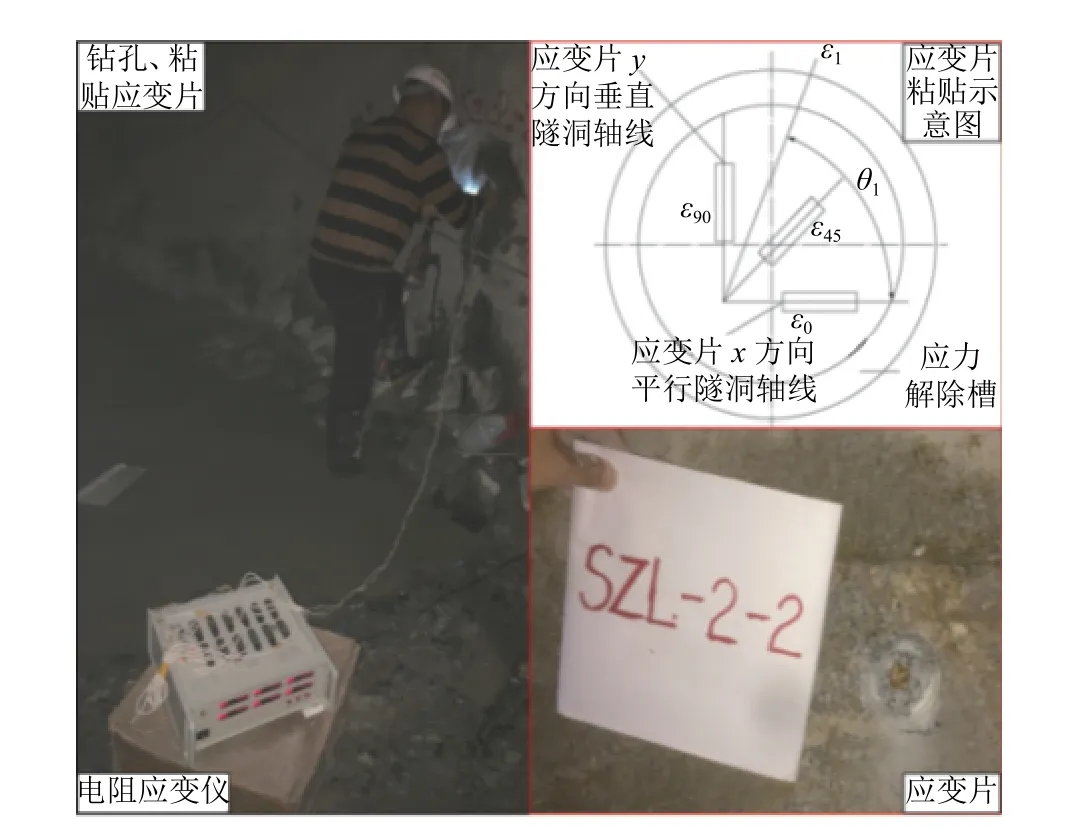
圖4 實測洞壁二次應力Fig.4 In-situ secondary wall stress

根據桑珠嶺隧道的地應力場分布[22-23]以及基于桑珠嶺隧道二次修正后過的隧道軸線全線應力場[18]模擬隧道開挖，計算范圍為DK177+600～DK187 +200，每個斷面的巖石單軸抗壓強度由現場點荷載試驗得到，巖體的物理力學參數由工程類比和現場試驗結果綜合確定[19-20]，具體巖爆判據制定流程見附加材料.

2.1 全線計算結果

對全線已發生的輕微、中等、強烈巖爆段進行數值模擬計算（計算方案見附加材料）后得到隧道開挖后的洞壁切向應力 σθ以及應力判據值 σθ/Rc如圖5所示，具體數值見附加材料表S1，表S1 中DK177 +600～DK186+200 段用作kNN 算法機器學習的樣本數據（共40 個），期望輸出按照以下方法確定：輕微巖爆時輸出為0，中等巖爆時輸出為1，強烈巖爆時輸出為2.預留DK186+300～187+200 段（共10 個）的數據作為驗證組，驗證此判據的準確度以及可靠性.

由圖5 可知：現場實際巖爆發生以輕微和中等為主，DK185+400～DK185+600 為強烈巖爆集中段；隧道花崗巖巖性段發生了輕微、中等、強烈三種等級的巖爆，而閃長巖巖性段只發生了輕微巖爆，巖爆發生對巖石巖性的敏感性還有待研究；樣本數據中輕微巖爆的 σθ/Rc值范圍在0.15～0.32，中等巖爆的 σθ/Rc值范圍在0.24～0.49，強烈巖爆的 σθ/Rc值范圍在0.42～0.59，各等級巖爆 σθ/Rc值的取值范圍有重疊部分，通過人為統計和篩選對預測結果存在較 大的干擾性，無法得出各等級巖爆的精確閾值.

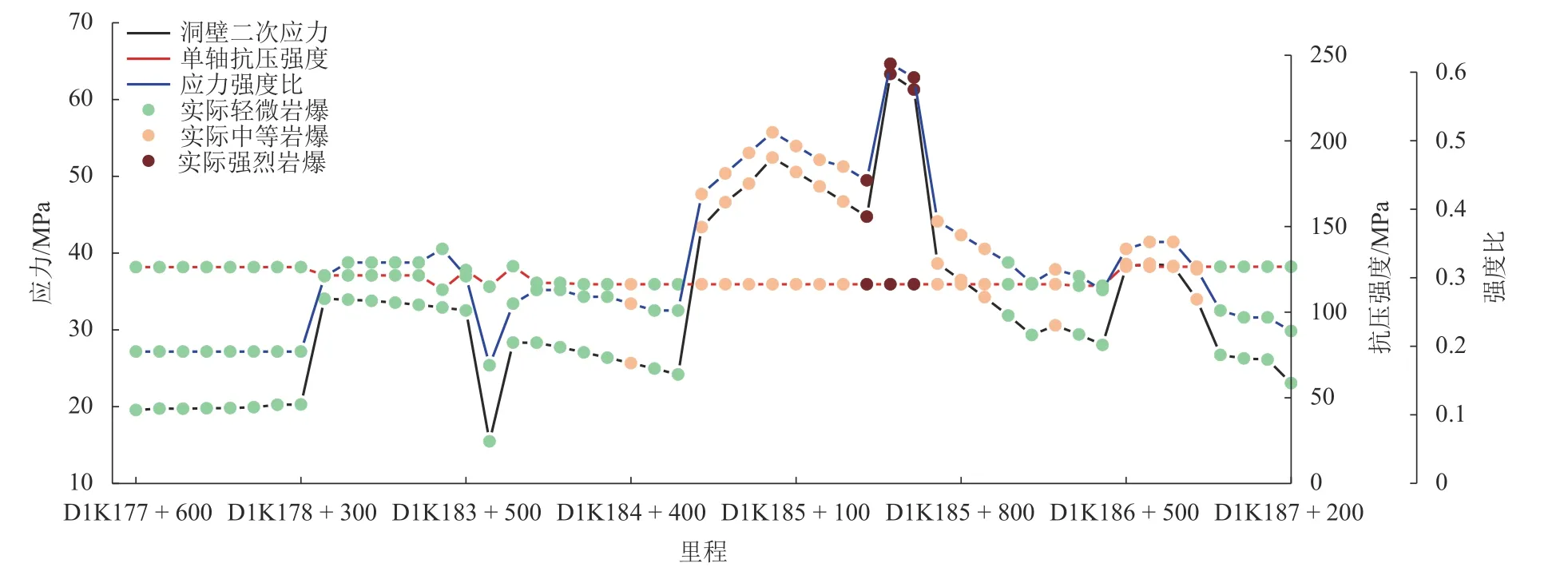
圖5 數值計算獲取得應力判據值及現場巖爆等級對應圖Fig.5 Corresponding diagram of stress criterion value obtained by numerical calculation and actual rockburst grades

2.2 判據提出

使用Python 對圖5 中DK177+600～DK186 +200 段樣本數據進行kNN 算法分類，圖5 中所有應力強度比值均在0.130～0.580 范圍內，在此范圍內，每隔0.001 設置一個虛擬數據點，用上述模型對這450 個數據點進行類別預測，即可得到輕微、中等、強烈巖爆各自的 σθ/Rc閾值.

經DK177+600～DK186+200 段樣本數據學習后的巖爆預測模型將0.130～0.580 范圍內450 個數據直觀地分為了3 個類別（表3），但是在各類別的臨界處還是有極少的浮動點，這是正常現象.取各類別開始趨于穩定（不再浮動）的第一個值為閾值，最終得到的拉林鐵路巖爆判據的結果是：當洞壁實測 0.13 ＜σθ/Rc≤0.31 時，預測有發生輕微巖爆的可能；當洞壁實測 0.31 ＜σθ/Rc≤0.54 時，預測有發生中等巖爆的可能；當洞壁實測 σθ/Rc＞0.54 時，預測有發生強烈巖爆的可能，結合前述分級標準，可得到完整的拉林鐵路巖爆分級標準及巖爆判據.

3 拉林鐵路巖爆判據的驗證及對比分析

3.1 與現有判據的對比分析

此次針對拉林鐵路巖爆判據研究選擇了 σθ/Rc作為判定指標，而現有的巖爆判據中，盧森判據[7]、王元漢判據[24]、王蘭生判據[12]及關寶樹判據[25]用了同樣的判定指標，如圖6 所示.

從圖6 中可看出：拉林鐵路巖爆判據中各等級巖爆的 σθ/Rc閾值較王蘭生、王元漢判據而言普遍偏低，即王蘭生、王元漢判據會低估拉林鐵路桑珠嶺隧道的巖爆發生情況.關寶樹判據中各等級巖爆的σθ/Rc閾值明顯低于拉林鐵路巖爆判據，即關寶樹判據會高估拉林鐵路桑珠嶺隧道的巖爆發生情況.與盧森判據相比，除了無巖爆、輕微巖爆的閾值較盧森判據偏低以外，其余各等級巖爆的 σθ/Rc與盧森判據相當，即盧森判據可以很好地預測拉林鐵路桑珠嶺隧道中等、強烈巖爆，但會低估輕微巖爆的發生情況.

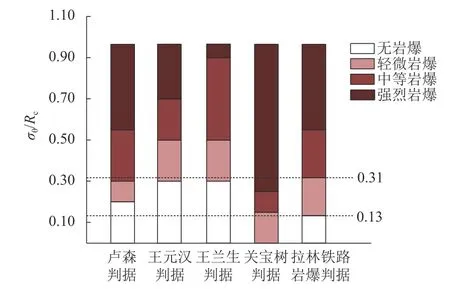
圖6 拉林鐵路巖爆判據與現有常用判據對比Fig.6 Comparison between existing common criterias and rockburst criteria of Lhasha-Linzhi railway

總之，拉林鐵路巖爆判據是在桑珠嶺隧道現場巖爆發育特征和規律、現場巖爆實際記錄、現場洞壁二次應力量測、現場巖樣點荷載試驗、基于二次修正地應力場的開挖模擬及kNN 算法的基礎上形成的一套完整的巖爆預測體系.

3.2 可靠性驗證

3.2.1 桑珠嶺隧道預留數據驗證

將圖5 中預留的DK186+300～187+200 段使用2.2 節提出的應力強度比（σθ/Rc）判據進行預測，可得到如表4 所示的結果.

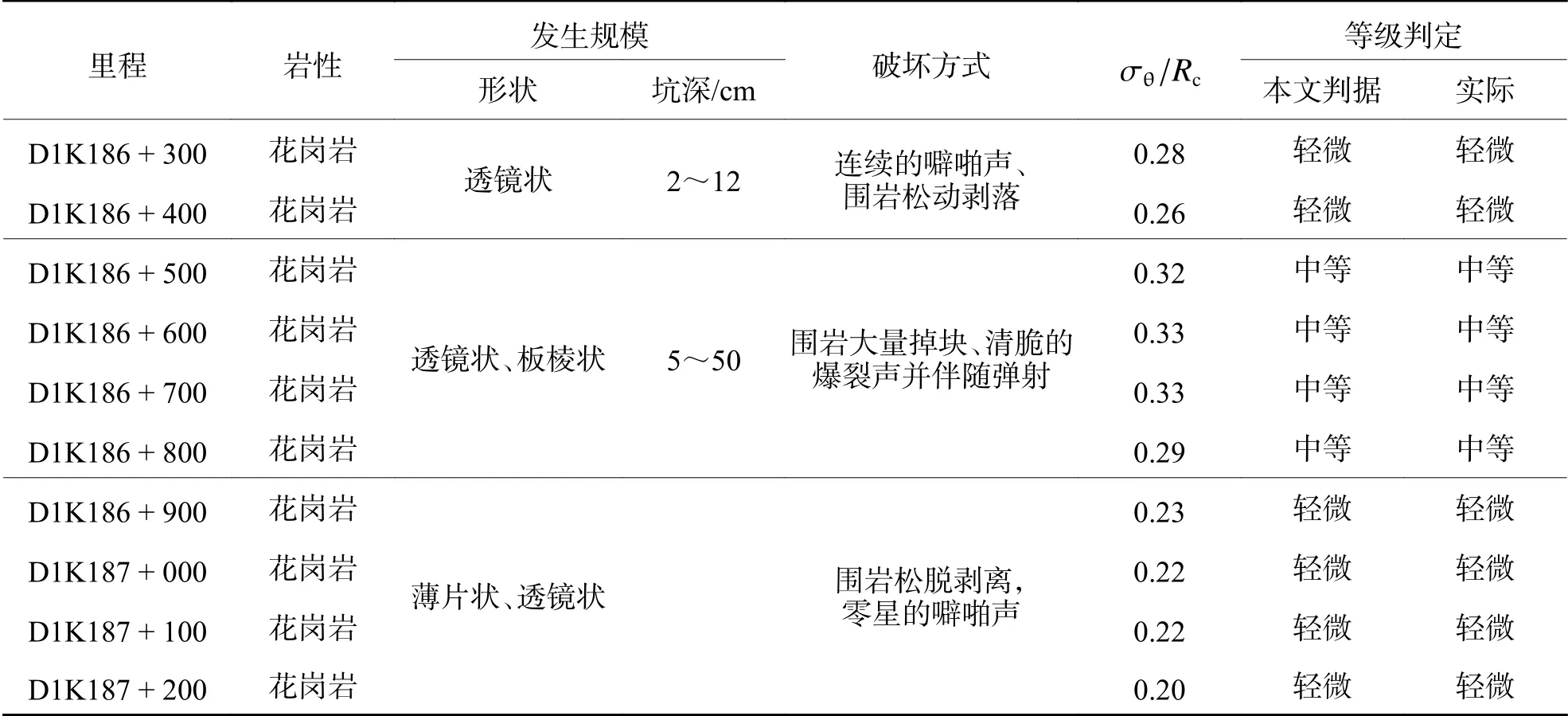
表4 桑珠嶺隧道DK186+300～187+200 段巖爆預測結果驗證Tab.4 Verification of rockburst prediction results of section DK186+300～187+200 in the Sangzhuling tunnel

基于kNN 算法的 σθ/Rc巖爆判據對DK186 +300～DK187+200 段的巖爆預測結果與實際巖爆等級相同，顯示了良好的精度，驗證了在一定量已有巖爆數據基礎上建立的巖爆預測模型的準確性和可靠性，在 σθ/Rc的閾值確定上，降低了人為因素對預測結果的干擾，具有良好的工程適用性.

3.2.2 拉林鐵路其他巖爆隧道驗證

拉林鐵路路線總長433 km，沿線隧道共46 座，占線路長度51.66%，除桑珠嶺隧道外，尚有包括祝拉崗隧道、達嘎拉隧道、崗木拉隧道等在內的多個典型巖爆隧道，都處于高地應力條件下，且隧址區以閃長巖、花崗巖等極硬巖為主，在施工中都出現了巖爆災害.因此，本節將采用基于桑珠嶺隧道巖爆實際發生情況提出的拉林鐵路巖爆烈度分級標準及判據在上述隧道中進行準確性和適用性檢驗.

收集已開挖的祝拉崗隧道、達嘎拉隧道、崗木拉隧道的地應力情況、地質情況及現場巖爆發生情況，為進一步說明拉林巖爆判據的準確性和適用性，同樣通過2.1 中的數值模型計算得到對應巖爆斷面的σθ/Rc值（計算參數如附加材料中表S1 所示），將各隧道現場實際巖爆發生等級與用拉林巖爆判據、盧森判據、王蘭生判據、關寶樹判據分別判定的巖爆等級進行橫向對比.

如圖7 所示，實柱體圖表示在各巖爆等級中該判據判定正確的次數，半透明柱體表示在各巖爆等級中，該判據做出判定的總次數，由上述各判據對3 座隧道的巖爆等級判定結果分析可知：

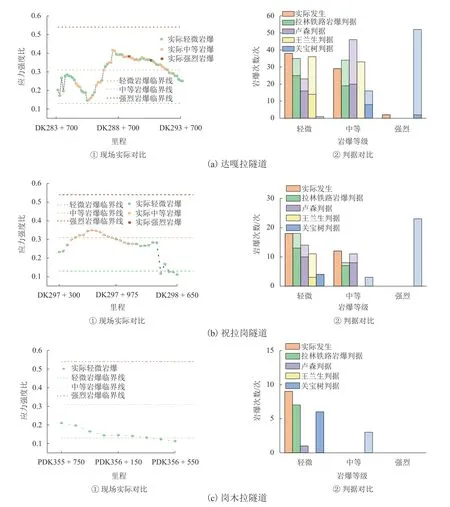
圖7 巖爆判定結果對比Fig.7 Comparison of rockburst results

1）采用拉林鐵路巖爆判據所判定的輕微、中等巖爆總次數與實際發生的輕微、中等巖爆總次數均接近，且對比實心柱體和透明柱體可知其判定準確率要明顯高于其他3 種判據.

2）采用盧森判據所判定的輕微巖爆次數遠遠小于實際發生次數，但其在中等巖爆等級中的判定表現較好，正確判定次數與正確率都與拉林鐵路巖爆判據相近，綜合來看，針對拉林鐵路而言，盧森判據判定能力低于拉林鐵路判據.

3）采用王蘭生判據所判定的輕微巖爆次數較多，但其正確率只有30%左右，實際發生的中等、強烈巖爆都沒有正確預測，說明針對拉林鐵路而言，王蘭生判據容易低估實際的巖爆發生等級.

4）采用關寶樹判據所判定的巖爆等級主要集中在強烈巖爆，而實際強烈巖爆極少發生，說明針對拉林鐵路而言，關寶樹判據嚴重高估了巖爆等級，可靠性較低.

綜合來看，對拉林鐵路而言，拉林鐵路巖爆判據的判定能力和預測準確率均高于其余判據，更具有適用性和針對性.

4 結 論

1）本研究中分析了巖爆發生的主要影響因素，選取 σθ/Rc作為判別拉林鐵路隧道巖爆的發生的指標，建立了以kNN 算法為基礎的巖爆預測模型，該方法利用桑珠嶺隧道工程已發生的實際巖爆情況及量測數據，對隧道未開挖段進行巖爆預測，較現有的巖爆應力判據更具有針對性和適用性.

2）在 σθ/Rc閾值的選取上利用了機器學習的方法，避免了人為因素對判據的影響，具有一定的科學性，且 σθ與Rc在施工過程中都易于獲取，這有利于在施工期對掌子面前方短距離范圍內進行精確的階段性巖爆預測.

3）在kNN 算法中，模型精度與樣本數據的數量大小有關，在本研究中用于基于kNN 算法的 σθ/Rc判據的樣本數據中，強烈巖爆的數據較少，在后續拉林鐵路乃至川藏線其他隧道的應用中應繼續添加強烈巖爆段的數據以提高巖爆預測模型的精度.

4）巖爆雖然是一種復雜的動力失穩地質災害，但依然有規律可循，本文中以桑珠嶺隧道為依托提出的拉林鐵路巖爆判據經過拉林鐵路達嘎拉隧道、祝拉崗隧道、崗木拉隧道的驗證，并與現有典型判據進行判定結果的對比分析，證實了其對于拉林鐵路巖爆隧道的適用性及準確性，可為后續川藏鐵路類似隧道的巖爆預測提供參考.

備注：附加材料在中國知網本文的詳情頁中獲取.