高碳鋼絲多道次拉拔及矯直對(duì)殘余應(yīng)力的影響

蔡 磊，朱建國，程 亮,，張帥今，唐 斌

(1. 盛利維爾(中國)新材料技術(shù)股份有限公司，江蘇 常州 213000)(2. 江蘇理工學(xué)院材料工程學(xué)院，江蘇 常州 213001)(3. 西北工業(yè)大學(xué) 凝固技術(shù)國家重點(diǎn)實(shí)驗(yàn)室，陜西 西安 710072)

1 前 言

冷拉拔高碳珠光體鋼絲具有極高的強(qiáng)度，是目前強(qiáng)度最高的鋼鐵制品[1]。由于其優(yōu)異的力學(xué)性能，拉拔鋼絲被廣泛用作輪胎簾線、焊絲、彈簧及切割絲等，在工業(yè)生產(chǎn)中占據(jù)重要地位[1-3]。然而，受拉拔本身工藝特性及摩擦的影響，鋼絲橫截面的變形很不均勻，從而在成形后產(chǎn)生殘余應(yīng)力。殘余應(yīng)力的存在顯著影響冷拔鋼絲的疲勞壽命、屈服強(qiáng)度等一系列使用性能[2-4]，因此拉拔過程及后處理過程中殘余應(yīng)力的形成與演變行為受到國內(nèi)外的廣泛關(guān)注。

目前，研究鋼絲殘余應(yīng)力的實(shí)驗(yàn)方法主要包括衍射法、切口法、鉆孔法等[3]。受限于鋼絲尺寸，其中切口法、鉆孔法等破壞性測量法不適用于細(xì)絲；而無損測量如衍射法等只能檢測鋼絲表面的殘余應(yīng)力。利用X射線，Willemse等[5]及Yang等[6]采用逐層剝蝕的方式衍射測量出了鋼絲從表層到心部的殘余應(yīng)力分布，然而這種方法效率低下且成本較高。隨著計(jì)算機(jī)及數(shù)值分析技術(shù)的發(fā)展，采用彈塑性有限元理論分析鋼絲拉拔過程中的殘余應(yīng)力演變逐漸成為一種有力手段。基于Ansys、Abaqus、Deform-3D等有限元數(shù)值仿真平臺(tái)[7-9]，人們能夠方便、快速地對(duì)拉拔成形過程中的多物理場進(jìn)行全過程追蹤，從而揭示拉拔成形過程中殘余應(yīng)力的形成和演變規(guī)律。數(shù)值仿真已經(jīng)成為研究鋼絲拉拔成形規(guī)律的主要手段之一，然而目前針對(duì)殘余應(yīng)力的研究主要集中在單道次拉拔，對(duì)于中間道次的殘余應(yīng)力演化以及后續(xù)矯直過程對(duì)殘余應(yīng)力的影響還需進(jìn)一步研究[4]。因此，本研究針對(duì)T9高碳鋼在多道次拉拔過程及后續(xù)拉伸矯直過程中的殘余應(yīng)力演變進(jìn)行研究，進(jìn)而揭示拉拔道次及拉伸矯直對(duì)殘余應(yīng)力的影響，為拉拔工藝優(yōu)化及鋼絲性能提升提供理論借鑒。

2 實(shí)驗(yàn)方法及有限元模型

本研究所使用的拉拔材料為正火態(tài)的T9高碳鋼盤條，其初始直徑為1.8 mm。經(jīng)8個(gè)道次拉拔后直徑變?yōu)?.9 mm，每道次平均壓縮率約為16%。拉拔所采用的模具為金剛石拉絲模，半模角為5°，定徑帶長度為鋼絲直徑的0.3倍。為了獲得每道次變形對(duì)鋼絲力學(xué)性能的影響，同時(shí)為數(shù)值模擬提供材料模型，對(duì)不同道次拉拔后的鋼絲進(jìn)行了拉伸實(shí)驗(yàn)，獲得的應(yīng)力應(yīng)變曲線如圖1所示。由圖1可以看出，隨著變形道次的累積，鋼絲發(fā)生加工硬化，其抗拉強(qiáng)度逐漸提升。

基于Abaqus有限元數(shù)值仿真平臺(tái)建立了鋼絲拉拔模型。為了減小網(wǎng)格規(guī)模、簡化計(jì)算過程，采用軸對(duì)稱的方式建模，如圖2所示。其中拉絲模約束為剛體，忽略其變形；鋼絲則采用彈塑性CAX4R單元進(jìn)行離散。為了避免局部效應(yīng)同時(shí)減小網(wǎng)格規(guī)模，鋼絲的初始長度設(shè)置為20 mm。考慮到鋼絲表層的軸向剪切效應(yīng)較為顯著，采用表層密、心部疏的梯度化網(wǎng)格以提高模擬結(jié)果的準(zhǔn)確性。根據(jù)圖1所示的拉伸實(shí)驗(yàn)結(jié)果，鋼絲盤條的彈性模量為210 GPa，屈服強(qiáng)度為825 MPa，硬化曲線按照?qǐng)D1中不同道次的拉伸數(shù)據(jù)進(jìn)行插值、優(yōu)化后獲得，如圖1中粗線所示。由于在實(shí)際拉拔過程中，鋼絲與拉絲模之間充分潤滑，且循環(huán)流動(dòng)的潤滑液能夠及時(shí)帶走熱量，因此在進(jìn)行拉拔模擬時(shí)將鋼絲視為率無關(guān)材料，忽略其變形產(chǎn)熱效應(yīng)。

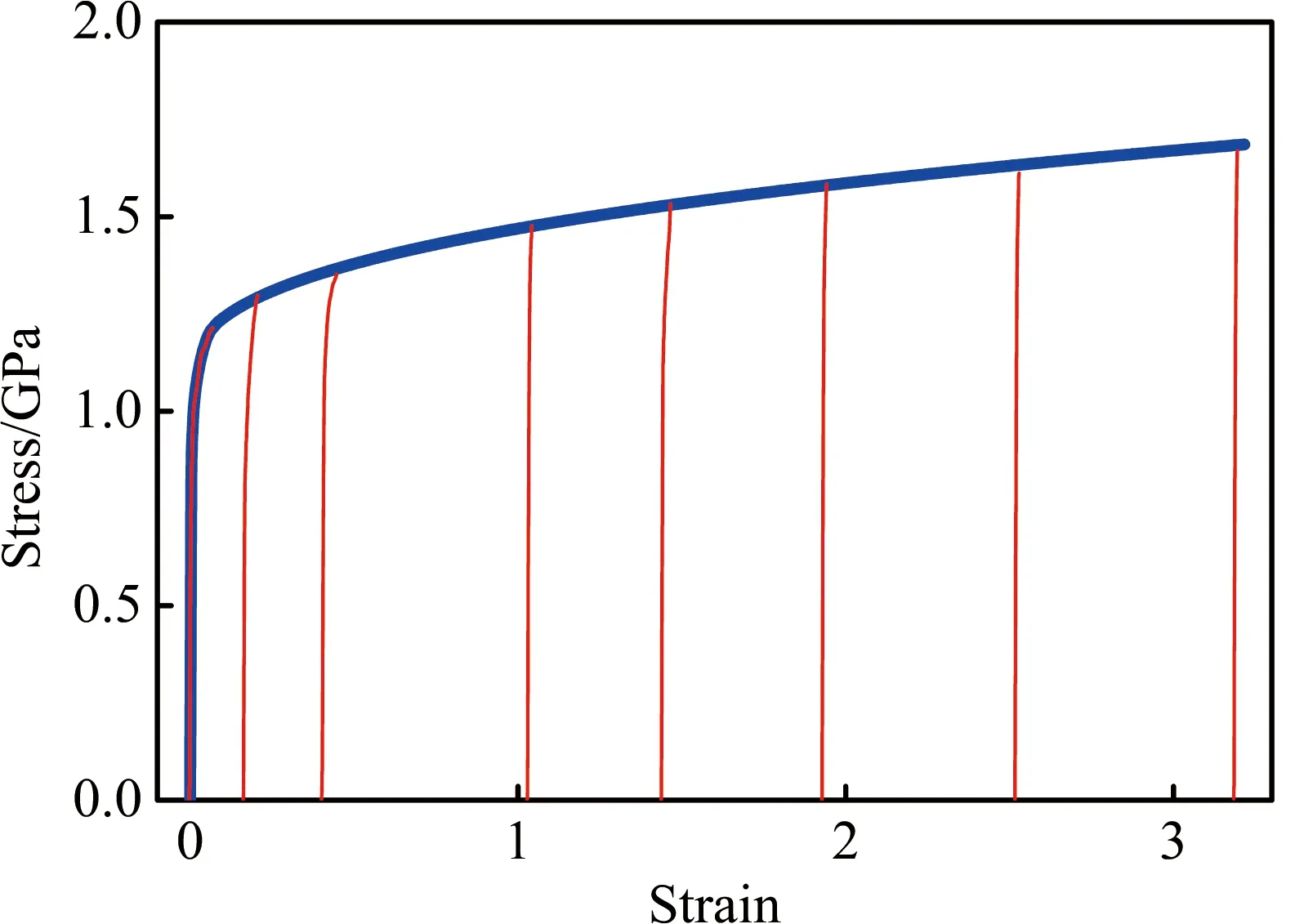
圖1 拉拔鋼絲的應(yīng)力應(yīng)變曲線。其中細(xì)實(shí)線為各道次拉拔后鋼絲實(shí)測應(yīng)力應(yīng)變曲線，粗實(shí)線為插值獲得的完整應(yīng)力應(yīng)變曲線Fig.1 Tensile stress-strain curves of the steel wire. The thin lines are the measured stress-strain curves after various drawing-passes, the thick line is the stress-strain curve obtained by interpolation

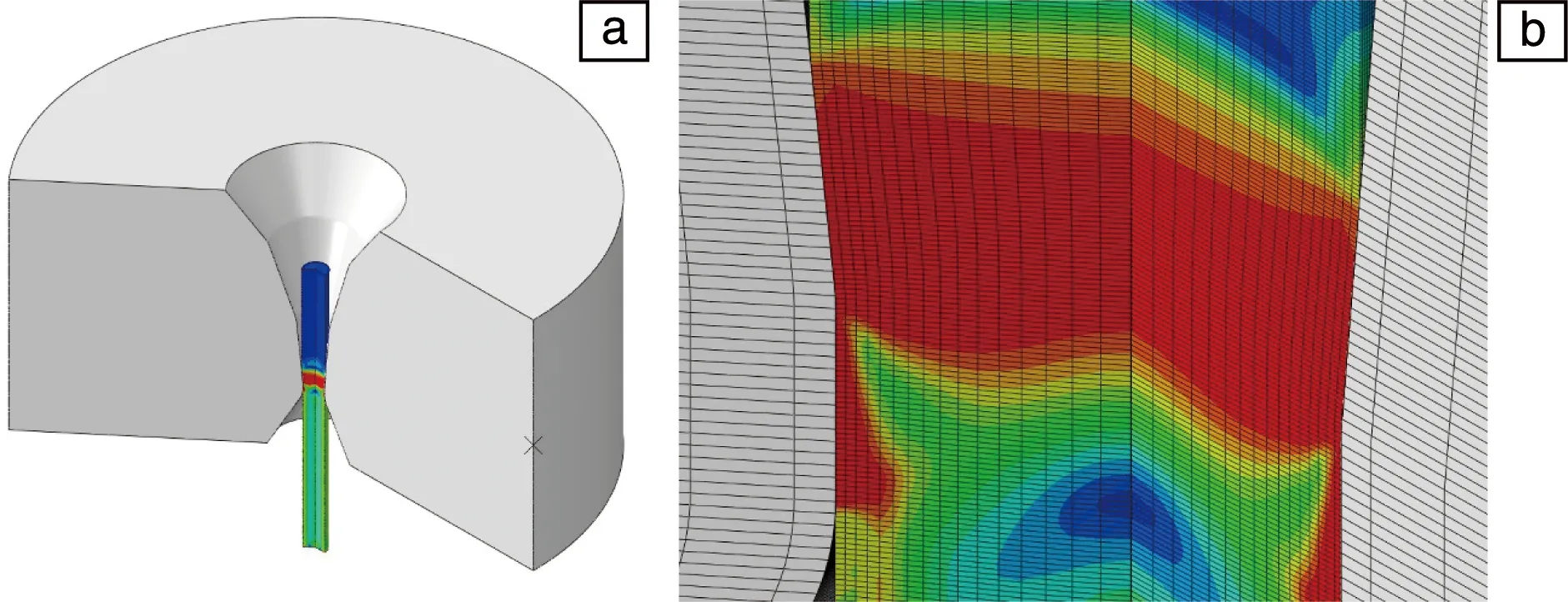
圖2 鋼絲拉拔有限元模型(a)，變形區(qū)的放大圖(b)Fig.2 Numerical model for the steel wire drawing(a), the enlarged map of the deformed region(b)

為了驗(yàn)證數(shù)值模型的可靠性，本研究將經(jīng)8道次拉拔后的鋼絲進(jìn)行單向拉伸模擬，并將獲得的應(yīng)力應(yīng)變曲線與實(shí)驗(yàn)數(shù)據(jù)進(jìn)行對(duì)比，結(jié)果如圖3所示。可以看到，預(yù)測的鋼絲拉伸應(yīng)力應(yīng)變曲線與實(shí)測曲線幾乎完全吻合。此外，預(yù)測的鋼絲均勻延伸率約為1.2%，隨后產(chǎn)生頸縮。由于模型并未考慮斷裂，因此不能直觀地預(yù)測其斷裂延伸率。然而無論是實(shí)際的應(yīng)力應(yīng)變曲線(圖3)還是文獻(xiàn)[1]中的斷口照片，均表明高碳鋼絲在單向拉伸時(shí)的應(yīng)力應(yīng)變曲線無顯著降低、幾乎不產(chǎn)生頸縮，即斷裂延伸率約等于均勻延伸率。由此可知，經(jīng)8道次拉拔后，采用所建立的數(shù)值模型預(yù)測的鋼絲延伸率約為1.2%。而實(shí)測鋼絲延伸率為1.1%，兩者幾乎一致。通過以上對(duì)比說明所建立的數(shù)值模型可靠程度高、模擬結(jié)果準(zhǔn)確性好。

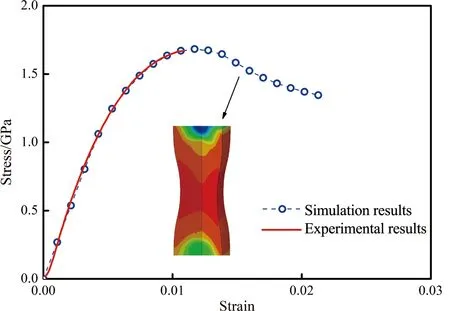
圖3 經(jīng)8道次拉拔后鋼絲的應(yīng)力應(yīng)變曲線Fig.3 Tensile stress-strain curves of the steel wire after 8 drawing-passes

3 結(jié)果與討論

3.1 殘余應(yīng)力分布特征

拉拔鋼絲在徑向、軸向和切向3個(gè)方向上均存在殘余應(yīng)力，其中軸向殘余應(yīng)力最為突出，因此也最受關(guān)注[10]。為了分析拉拔后軸向殘余應(yīng)力的分布特征，對(duì)經(jīng)第一道次拉拔后的鋼絲取中間橫截面的徑向路徑進(jìn)行分析，獲得從中心到邊緣的節(jié)點(diǎn)殘余應(yīng)力值，如圖4所示。由圖中可以看出鋼絲經(jīng)拉拔后，心部的軸向殘余應(yīng)力為壓應(yīng)力，且絕對(duì)值非常大；隨著向表層靠近，軸向應(yīng)力的絕對(duì)值逐漸減小，并在相對(duì)位置約0.65處變?yōu)?，然后轉(zhuǎn)變?yōu)槔瓚?yīng)力并逐漸提高，在表層一定深度內(nèi)達(dá)到最大值且隨后不再顯著變化。這種變化規(guī)律與其他文獻(xiàn)中用衍射法獲得的實(shí)測變化規(guī)律保持一致[2]，從而再次驗(yàn)證了模擬結(jié)果的有效性。

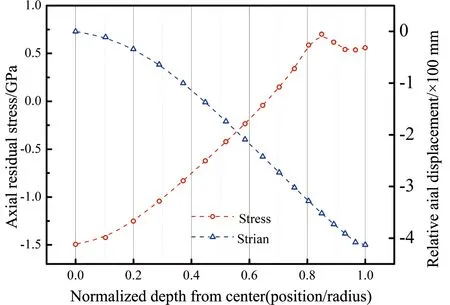
圖4 第一道次拉拔結(jié)束后鋼絲的軸向殘余應(yīng)力及橫截面的軸向相對(duì)位移分布Fig.4 Distribution of the axial residual stress and relative axial displacement of the cross-section of the steel wire after the first drawing-pass

鋼絲的軸向殘余應(yīng)力主要是由于表層和心部金屬流動(dòng)速度的差異所導(dǎo)致的。影響拉拔過程中金屬流動(dòng)速度的因素主要有兩點(diǎn)，一是鋼絲表面與拉絲模之間的摩擦阻礙了表層金屬的流動(dòng)，二是錐形的模孔使鋼絲表層材料的移動(dòng)距離加長。在這兩種因素的作用下，鋼絲表層的軸向流動(dòng)速度滯后于心部。為了保持鋼絲的整體性，心部區(qū)域必然為表層施加額外的附加拉應(yīng)力以促進(jìn)其流過模孔。相應(yīng)地，鋼絲心部則受到附加壓應(yīng)力作用。由此可知，軸向殘余應(yīng)力的產(chǎn)生是鋼絲橫截面流動(dòng)速度不均勻的結(jié)果，因而其性質(zhì)和分布規(guī)律可以用變形后橫截面的相對(duì)移動(dòng)進(jìn)行解釋：

Si=Ui-U1

(1)

其中，Si為徑向路徑上第i個(gè)節(jié)點(diǎn)相對(duì)于中心節(jié)點(diǎn)的軸向相對(duì)位移，Ui為第i個(gè)節(jié)點(diǎn)的軸向位移，U1為中心節(jié)點(diǎn)的軸向位移。徑向路徑節(jié)點(diǎn)的相對(duì)位移如圖4所示，可以明顯看到，越接近表層，節(jié)點(diǎn)的相對(duì)位移的絕對(duì)值越大，其流動(dòng)越滯后于心部，整體上呈反S型分布，恰好與軸向殘余應(yīng)力的正S型分布相對(duì)應(yīng)，從而解釋了鋼絲外正內(nèi)負(fù)的軸向殘余應(yīng)力分布特征。

3.2 拉拔道次對(duì)殘余應(yīng)力的影響

拉拔道次對(duì)軸向殘余應(yīng)力的影響如圖5所示。可以看到，隨著拉拔道次的增加，鋼絲心部的殘余壓應(yīng)力有所提高，表層的殘余拉應(yīng)力也略微增大，說明拉拔道次在一定程度上增加了殘余應(yīng)力的不均勻性，然而其影響并不顯著。根據(jù)前面的分析可知，軸向殘余應(yīng)力的大小取決于鋼絲在穿過模孔時(shí)橫截面各個(gè)部位的相對(duì)流動(dòng)速度，而與變形量的絕對(duì)值無關(guān)。因此，鋼絲在第一道次拉拔后即確立了殘余應(yīng)力的分布特征。在后續(xù)拉拔道次中，由于變形條件與第一道次相差不大，鋼絲在穿過模孔時(shí)不同道次之間表層與心部的速度差變化不明顯，因此鋼絲維持了第一道次的殘余應(yīng)力分布規(guī)律。總而言之，隨著拉拔道次的增加，雖然累積變形量顯著提高，但僅略微加劇了軸向殘余應(yīng)力分布的不均勻性，整體而言殘余應(yīng)力的變化不顯著。

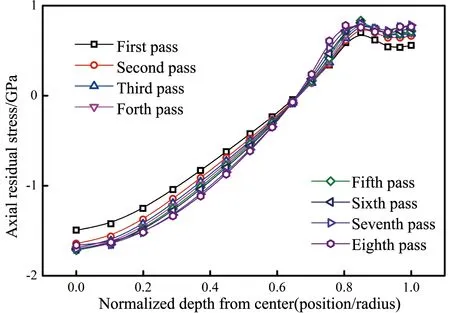
圖5 不同道次拉拔后鋼絲橫截面的軸向殘余應(yīng)力分布Fig.5 Distribution of the axial residual stress of the cross-section of the steel wire after various drawing-passes

3.3 拉伸矯直對(duì)殘余應(yīng)力的影響

拉拔鋼絲在成品前往往需要經(jīng)過一道矯直工序。矯直的本質(zhì)是引入少量的塑性變形以改善鋼絲內(nèi)部的應(yīng)力分布，從而使彎曲的鋼絲變直。為了研究少量塑性變形對(duì)鋼絲殘余應(yīng)力的影響，本研究將經(jīng)8道次拉拔后的鋼絲分別施加0.2%～1%的拉伸變形量后卸載，分析少量軸向變形對(duì)殘余應(yīng)力的影響。

在無殘余應(yīng)力的前提下，當(dāng)鋼絲承受單軸拉應(yīng)力時(shí)各個(gè)部位將均勻變形，即橫截面上各個(gè)節(jié)點(diǎn)的軸向運(yùn)動(dòng)保持同步。而當(dāng)存在殘余應(yīng)力時(shí)，各節(jié)點(diǎn)可能由于變形抗力的不同而造成軸向移動(dòng)不同步。如前所述，各節(jié)點(diǎn)之間相對(duì)位移的大小直接關(guān)系到軸向殘余應(yīng)力的分布。因此，為了定量分析拉伸加載過程中鋼絲橫截面上各節(jié)點(diǎn)的軸向移動(dòng)情況，本研究引入相對(duì)位移差這一變量，其表達(dá)式為：

(2)

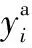
圖6為不同拉伸變形量下鋼絲橫截面節(jié)點(diǎn)的相對(duì)位移差，可以看到在殘余應(yīng)力的作用下，鋼絲在伸長過程中橫截面的移動(dòng)是不同步的，表層的相對(duì)位移量大于心部，而且隨著拉伸變形量的增大，鋼絲表層的相對(duì)位移差顯著增大。這主要是由于鋼絲在矯直前的殘余應(yīng)力為內(nèi)負(fù)外正，當(dāng)鋼絲在矯直過程中承受拉應(yīng)力時(shí)，在應(yīng)力疊加的作用下鋼絲表層的拉應(yīng)力進(jìn)一步提高，從而使表層區(qū)域更容易發(fā)生軸向伸長。這種變形的不同步也能夠從圖7所示的屈服范圍云圖中得以體現(xiàn)。可以明顯看到，隨著拉伸的進(jìn)行，鋼絲殘余拉應(yīng)力最大的區(qū)域(亞表層)先發(fā)生屈服并逐漸擴(kuò)展至整個(gè)表層拉應(yīng)力區(qū)，然后再逐步向心部壓應(yīng)力區(qū)擴(kuò)展。

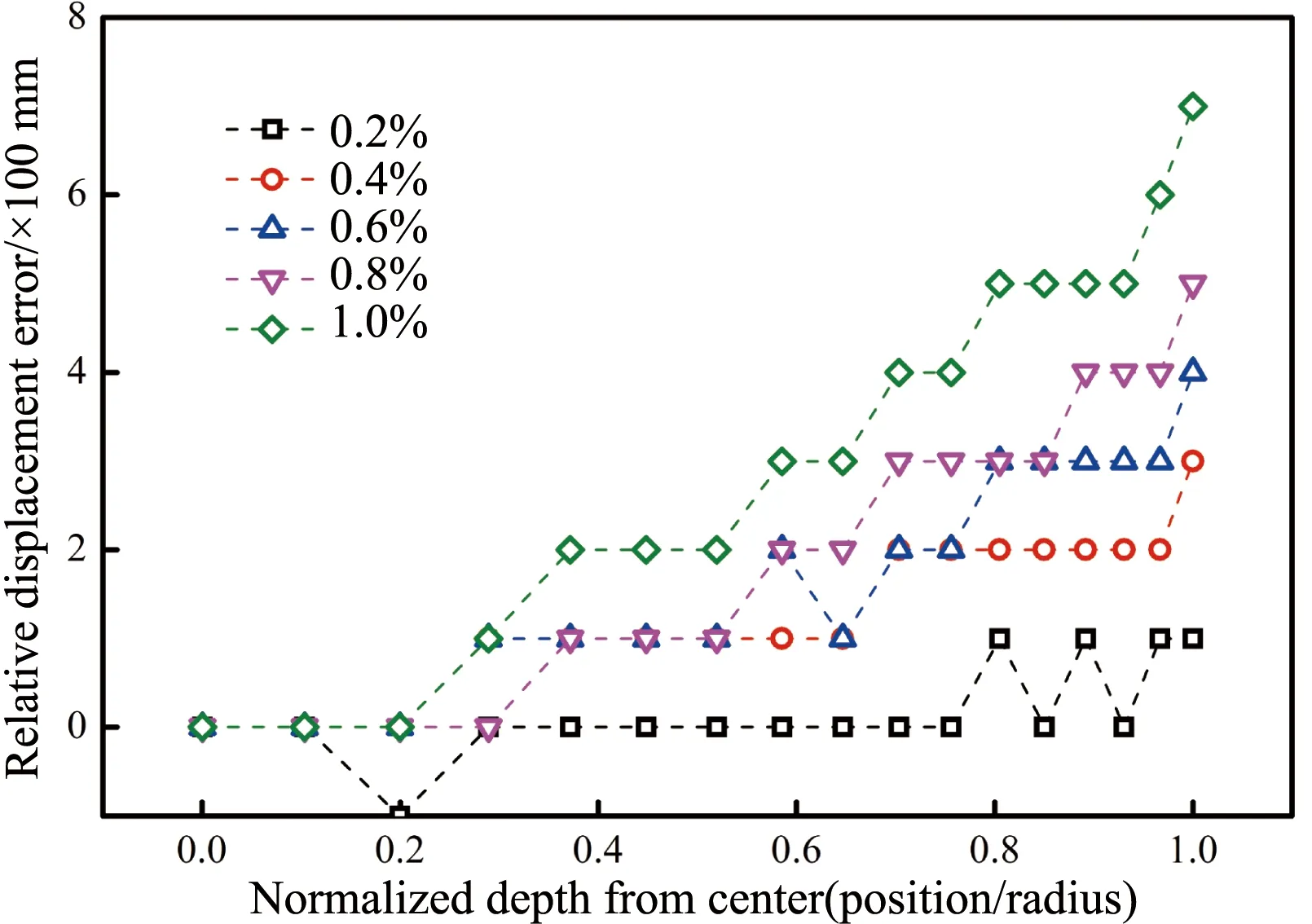
圖6 不同拉伸變形量下鋼絲橫截面節(jié)點(diǎn)的相對(duì)位移差Fig.6 Relative displacement error of the cross-section of the steel wire at various tensile deformation

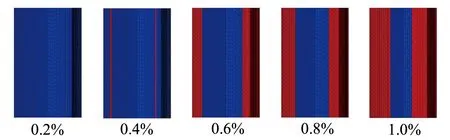
圖7 不同拉伸量下鋼絲屈服范圍的變化，紅色區(qū)域?yàn)榍^(qū)，藍(lán)色區(qū)域?yàn)槲辞^(qū)Fig.7 Evolution of the yield area at various tensile elongations, the red regions denote the yield area while the blue regions are the area that has not yield

前文指出，在拉拔過程中鋼絲表層的流速小于心部，從而造成內(nèi)負(fù)外正的軸向殘余應(yīng)力分布；而在拉伸矯直過程中材料流動(dòng)則表現(xiàn)出相反的趨勢，表層流速較快而心部較慢。可想而知，通過這種流速補(bǔ)償，拉伸矯直可能能夠有效改善鋼絲的軸向殘余應(yīng)力。為了驗(yàn)證這一點(diǎn)，本研究對(duì)拉伸—卸載后鋼絲的軸向殘余應(yīng)力分布進(jìn)行了分析，如圖8所示。可以看到，當(dāng)拉伸變形量小于0.4%時(shí)，與初始狀態(tài)相比殘余應(yīng)力幾乎沒有任何變化。這主要是由于變形量較小，不足以引起鋼絲顯著的塑性變形所致(圖7)。隨著拉伸量的進(jìn)一步提高，最大壓應(yīng)力和拉應(yīng)力均開始降低，且降低幅度越來越大，殘余應(yīng)力的分布均勻性得到了顯著改善。

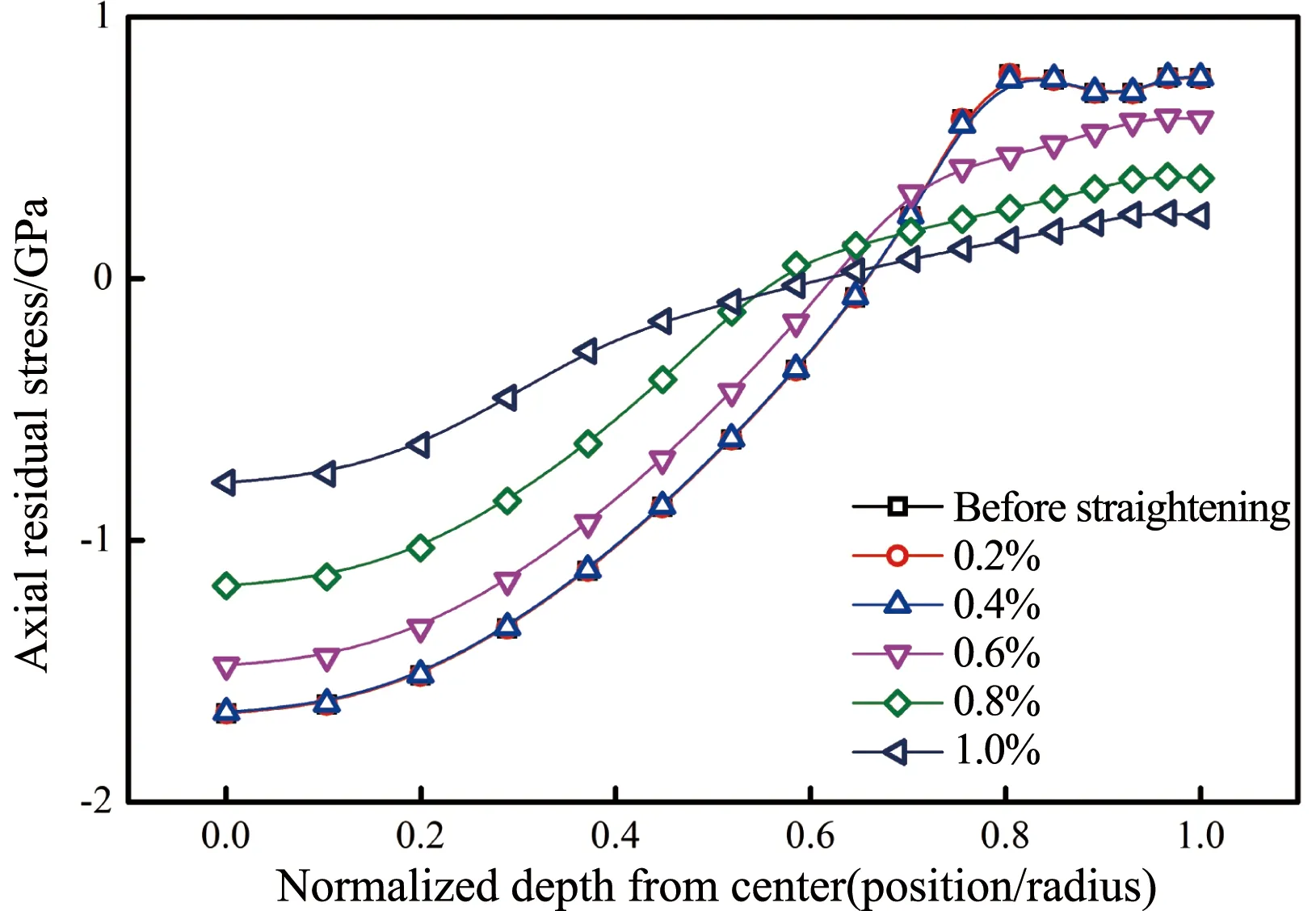
圖8 拉伸變形量對(duì)軸向殘余應(yīng)力分布的影響Fig.8 Effect of tensile deformation on the distribution of axial residual stress

由此可見，給與拉拔鋼絲一定的軸向拉伸是改善其殘余應(yīng)力分布的有效手段，而且拉伸變形越大效果越顯著。然而，值得注意的是，鋼絲經(jīng)8道次拉拔后的延伸率僅為1.1%，因此拉伸矯直量應(yīng)控制在1%以下，避免鋼絲在矯直過程中發(fā)生斷裂。

4 結(jié) 論

本研究主要對(duì)T9高碳珠光體鋼絲在多道次拉拔及后續(xù)拉伸矯直過程中的軸向殘余應(yīng)力進(jìn)行分析，所得主要結(jié)論如下：

(1)根據(jù)實(shí)際的鋼絲拉拔過程建立了有限元數(shù)值模型，并結(jié)合實(shí)驗(yàn)結(jié)果驗(yàn)證了模型的有效性。數(shù)值仿真的結(jié)果表明，鋼絲經(jīng)拉拔后表層為拉應(yīng)力，心部為壓應(yīng)力。拉拔道次的提高對(duì)軸向殘余應(yīng)力的影響較小。

(2)拉伸矯直能夠顯著改善軸向殘余應(yīng)力的分布規(guī)律。隨著拉伸變形量的提高，殘余應(yīng)力最大值顯著降低，殘余應(yīng)力分布更加均勻。然而，拉伸變形量的上限取決于鋼絲的延伸率，過大的拉伸矯直量會(huì)使鋼絲發(fā)生斷裂。