基于自適應MPC算法的軌跡跟蹤控制研究

王 銀，張灝琦，孫前來，李小松，孫志毅

太原科技大學 電子信息工程學院，太原030024

自動駕駛不僅可以減少因操作失誤而引起的交通事故的發生率，而且能夠提高貨物的運輸效率，因而自動駕駛技術成為當前國內外自動控制領域研究的熱點[1]。

車輛的軌跡跟蹤控制環節是自動駕駛系統中重要的一部分。軌跡跟蹤是指通過控制車輛轉向，使得車輛可以按照給定參考軌跡的路線行駛[2]。

目前，智能車輛的軌跡跟蹤控制問題受到了國內外廣大專家學者的重視。常用的軌跡跟蹤控制算法有魯棒控制、滑膜控制、模型預測控制（MPC）等。文獻[3]提出了一種增益調度、魯棒、共享的控制器來進行軌跡跟蹤。文獻[4]中的控制器采用了模糊CMAC 控制方法，該控制器可以消除擾動對系統的影響，使得機器人可以較為精確地跟蹤參考軌跡，并且一定程度上提高了行駛穩定性。章仁燮等[5]采用了一種條件積分算法的魯棒控制方法，控制器由運動學和動力學兩部分構成，保證側向偏差和橫擺角速度的漸進穩定，使得試驗車輛可以實現跟蹤期望軌跡的目標。文獻[6]提出的滑膜綜合控制器可以降低建模不確定性和擾動時的魯棒性。而MPC相比于其他控制算法來說，最大的優勢是多種約束可以在控制過程中被添加進去[7]。大多數學者都把提高軌跡跟蹤精度作為主要控制目標[8-10]。其中，文獻[11]把車輛行駛的穩定性也作為了控制目標，通過把前輪轉角作為控制量，根據MPC設計相應的控制器，可以實現較為穩定的跟蹤參考軌跡。文獻[12]提出了一種基于MPC 的新型路徑跟蹤框架，是一個多層控制系統，包括三個具有固定速度的路徑跟蹤控制器和一個速度決策控制器，可以根據路徑信息主動調整縱向速度，且有良好的跟蹤精度。文獻[13]采用運動學模型，基于MPC方法設計了考慮車輛動力學、執行器和狀態約束的路徑跟蹤控制器，以前輪轉向角為控制變量，使AGV的實際軌跡保持在一定的區域內并滿足安全要求。文獻[14]設計了集成主動前輪轉向和差動制動的MPC 控制器，實現了車輛的橫向穩定控制。劉凱等[15]針對越野地形的復雜環境，建立了特殊的車輛動力學模型，并且添加了車輛側傾安全約束。然后在考慮上述模型及約束條件的基礎上，設計了MPC 軌跡跟蹤控制器。眾多專家學者對MPC 軌跡跟蹤控制方面都做了大量的研究，且都有著不錯的跟蹤精度。但大多數都是處于定速且良好工況，然而實際應用中，車輛經常會處于加速減速且低附著的工況中，使得車速變化幅度大，極易造成軌跡跟蹤失敗，發生安全事故。

因此針對智能車輛在低附著且變速條件下跟蹤控制精確性和穩定性不高的問題，提出一種新型控制框架。通過添加側偏角約束，以及設計預測時域（Hp）控制器，建立了自適應的MPC 控制器，該控制器能夠根據車速的變化，實時產生Hp。在CarSim 與MATLAB/Simulink構建的聯合仿真實驗平臺進行試驗，仿真實驗結果表明自適應的MPC控制器能夠提高智能車輛在低附著且變速條件下跟蹤控制的精確性和穩定性。

1 車輛動力學模型

車輛的動力學模型是要作為控制器的預測模型使用，需要在較為準確地描述車輛動力學過程的基礎上盡可能地進行簡化，以減少控制算法的計算量。因此在車輛動力學建模時，要進行以下理想化假設：（1）忽略車輛垂向運動。（2）忽略車輛的懸架特性。（3）忽略輪胎橫、縱向耦合關系。（4）不考慮輪胎的橫向載荷轉移，以及認為輪距相對于轉彎半徑可以忽略不計，使用單軌模型來描述車輛。（5）忽略空氣阻力。

基于上述假設可以得到車輛的動力學模型，如圖1所示。

圖1 中，Flf、Flr為前后輪受到的縱向力；Fcf、Fcr為前后輪受到的側向力；Fxf、Fxr為前后輪受到的x方向的力；Fyf、Fyr為前后輪受到的y方向的力；δf為前輪偏轉角；αf為前輪側偏角；φ為橫擺角速度。

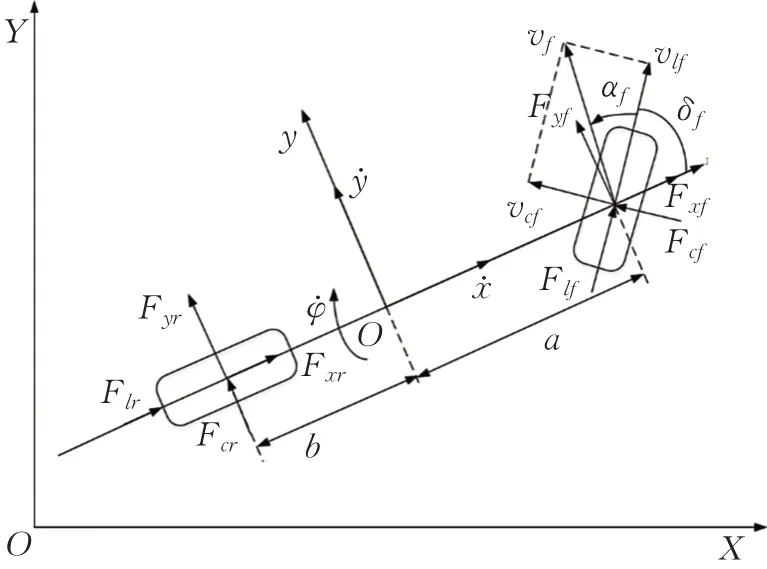
圖1 車輛單軌模型

根據牛頓第二定律、車身坐標轉換、輪胎受力，可得出車輛動力學模型。

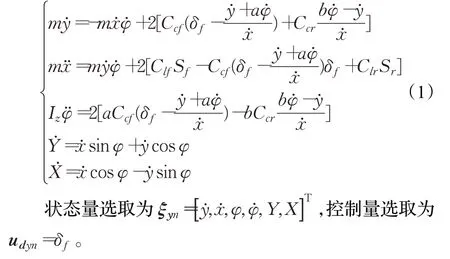
2 軌跡跟蹤控制

2.1 軌跡跟蹤控制架構

軌跡跟蹤控制架構主要由3 部分組成：MPC 控制器、CarSim車輛模型、Hp控制器。其中MPC控制器是實現軌跡跟蹤的核心部分，遵循預測模型、滾動優化和反饋校正的基本原理[16]。MPC 控制器根據參考軌跡和目標函數求解出最優的控制量δf，輸入到被控車輛模型中，得到當前的狀態，作為預測模型的輸入，預測時域控制器根據當前車速v求解出對應預測時域Hp，輸入到線性誤差預測模型中，然后重復上述過程，最終實現軌跡跟蹤。圖2為基于自適應MPC軌跡跟蹤控制器。

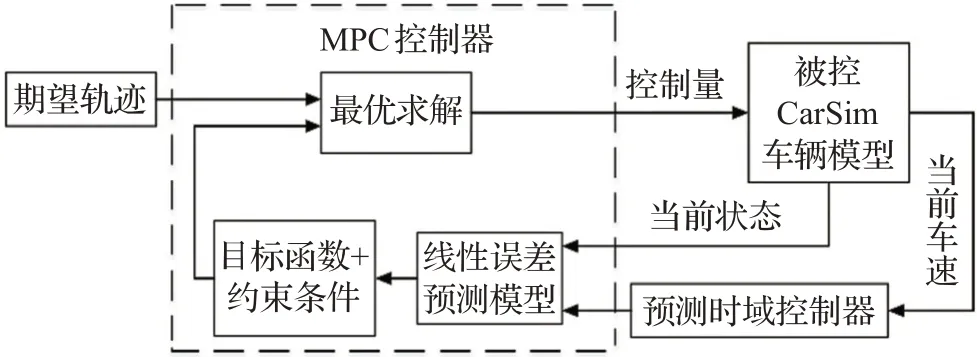
圖2 基于自適應MPC軌跡跟蹤控制器

2.2 MPC控制器的設計

2.2.1 線性誤差模型的建立

根據車輛非線性動力學模型可建立狀態空間表達式：

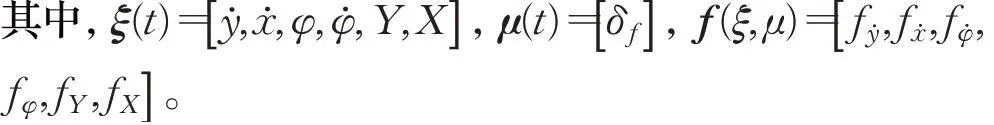
在t時刻將式（2）在工作點(ξ(t),μ(t-1))處線性化并離散化，得到離散的線性時變系統，如下：

根據式（3）、（5）設計模型預測控制器，首先將控制輸入由控制量μ(t)經過數學變換轉化為控制增量Δμ(t)，再做如下設定：

式中，0m×n是m×n維0矩陣；0m是m維列矩陣；Im是m維單位矩陣。

得到線性誤差表達式：

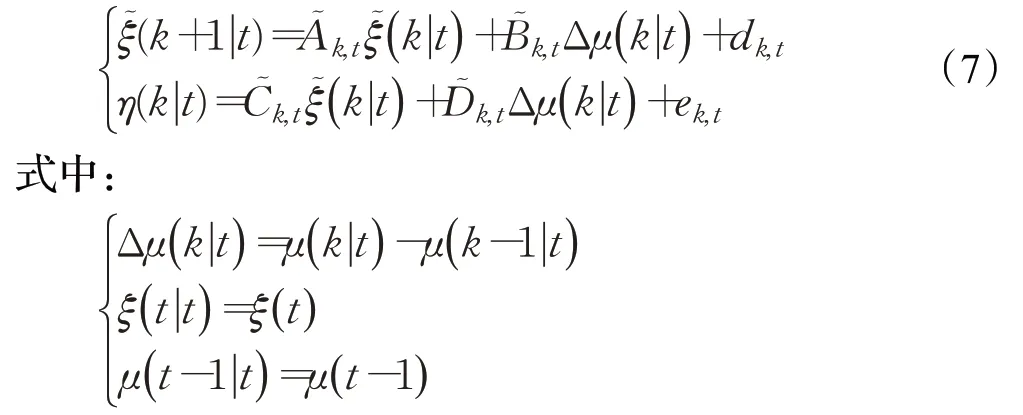
進一步地，可以得到在預測時域內Hp系統輸出量可用如下公式計算：

由式（8）可知預測時域Hp內輸出量的預測值Ytr(t)可通過當前t時刻已知的狀態量ξ(t|t)、上一時刻的控制量μ(t-1|t)以及控制時域Hc內未知的控制增量ΔU(t)計算得到。

2.2.2 目標函數的設計

由于系統的控制增量ΔU(t)是未知的，必須通過設定合理的優化目標進行求解，通過求解目標函數，可以得到一系列最優控制增量，并將序列中的第一個元素加入到狀態量和輸出量的求解中。

在預測控制中，一般考慮如下目標函數：

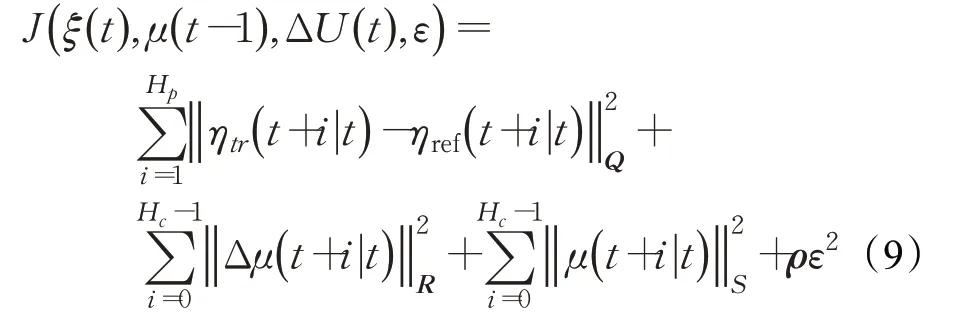
其中，Hp和Hc分別為預測時域和控制時域；ηref(t+i|t)為參考輸出量；Q、R、ρ為權重矩陣，ε為松弛因子。

式中第一項體現了控制系統對參考軌跡的跟蹤能力，第二項反映了系統對控制量平穩變化的要求，第三項反映了系統對控制量最值的要求。為了防止出現無解的情況，因此在目標函數中加入了松弛因子ε。

2.2.3 約束條件

為了保證系統對期望軌跡的精確跟蹤，以及保證行駛的穩定性，需要對控制量、控制增量進行約束，約束條件表達式如下：

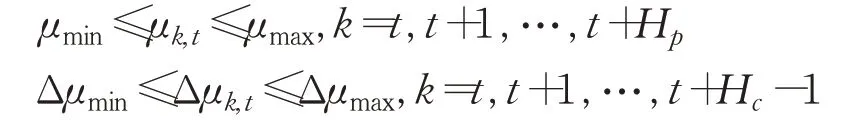
此外，為了解決車輛在低附著環境下行駛時因側滑而造成軌跡跟蹤失敗，應添加側偏角約束。

輪胎側偏角α與質心橫向速度、質心縱向速度、橫擺角速度以及前輪轉角δf之間的關系如下：

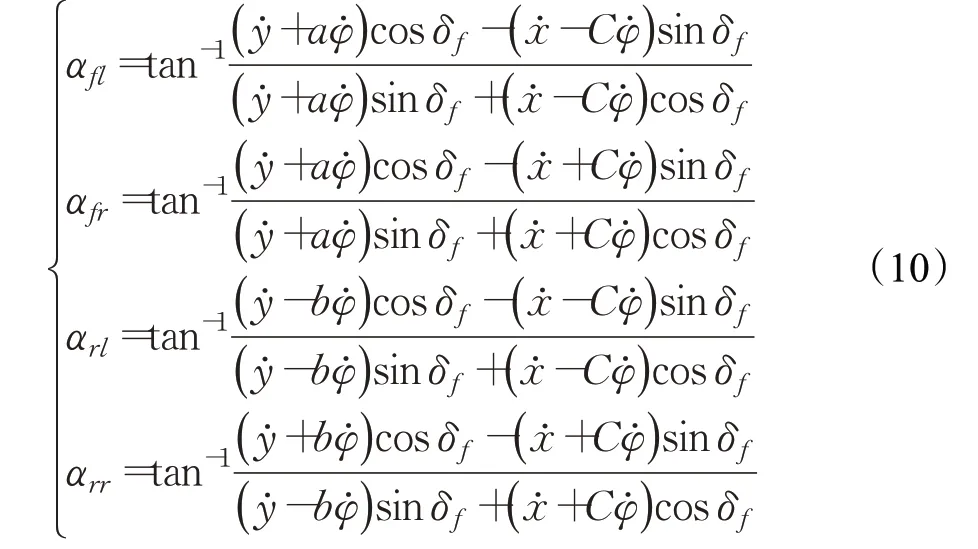
將上式進行線性化與離散化處理，得到離散線性時變系統，如下：

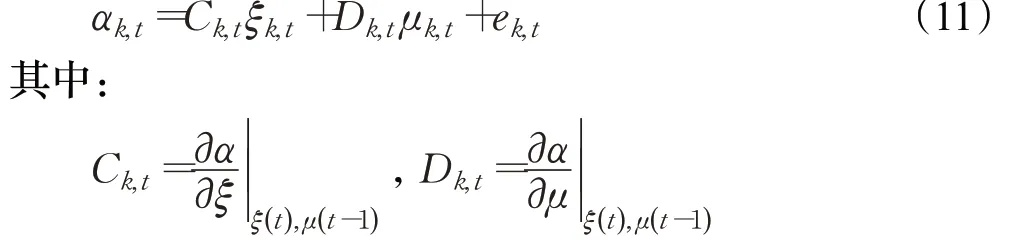
然后對側偏角添加約束條件：

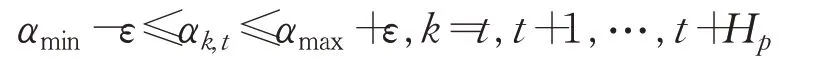
下面對比未添加側偏角約束控制器與添加側偏角約束控制器進行軌跡跟蹤的效果。本文參考軌跡如圖3所示。表達式如式（13）：

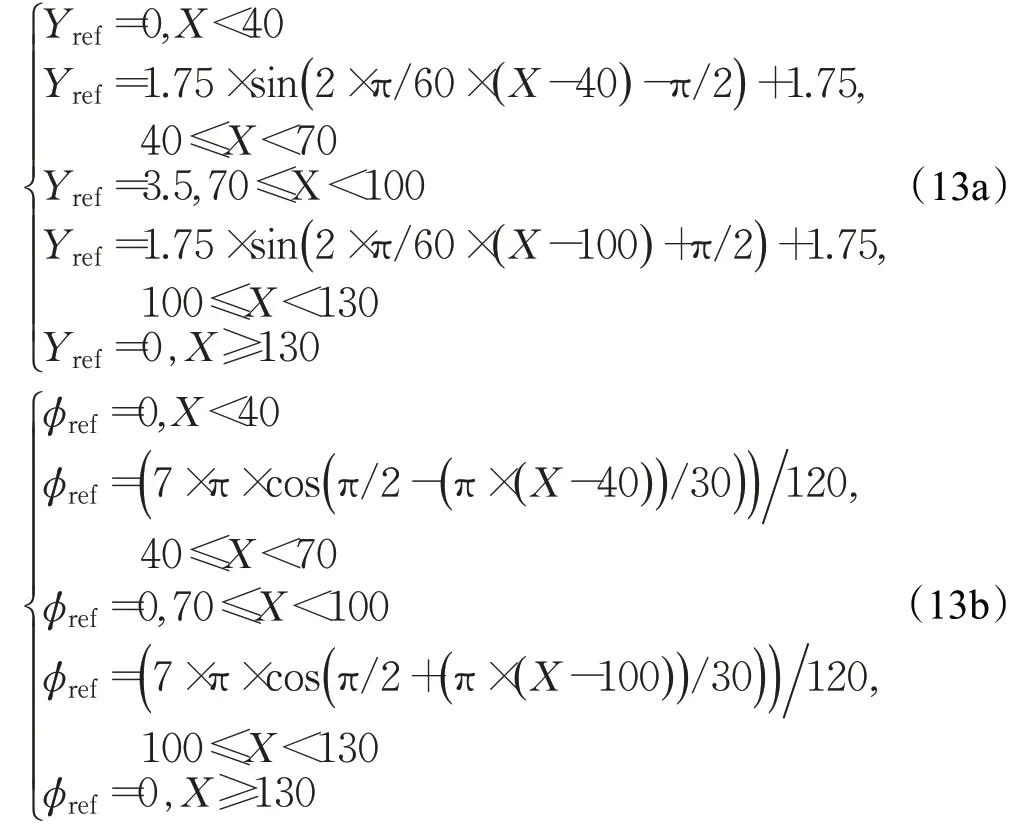
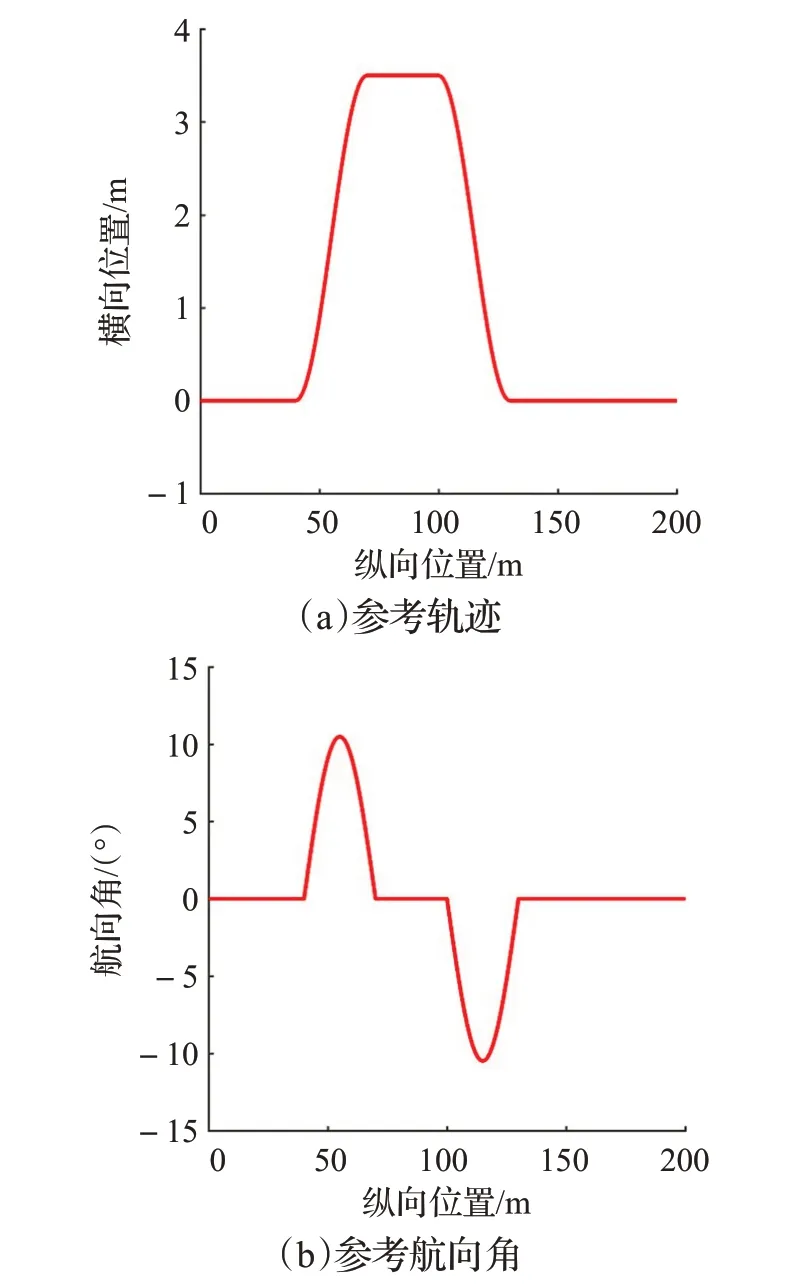
圖3 參考軌跡和參考航向

本文車輛參數如表1 所示，MPC 控制器參數如表2所示。

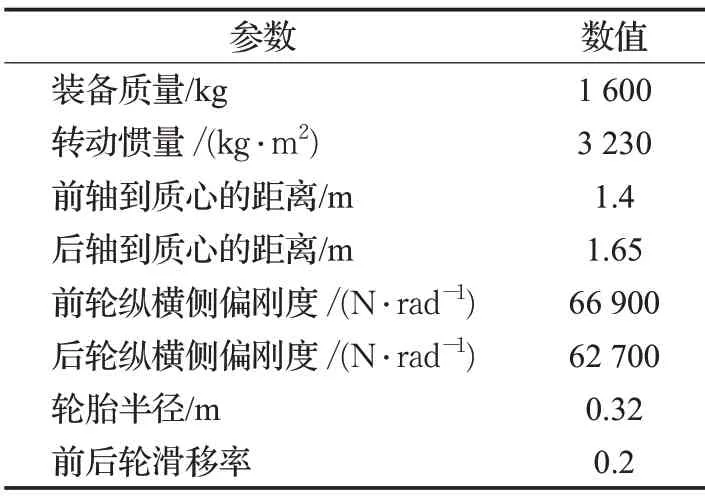
表1 車輛參數

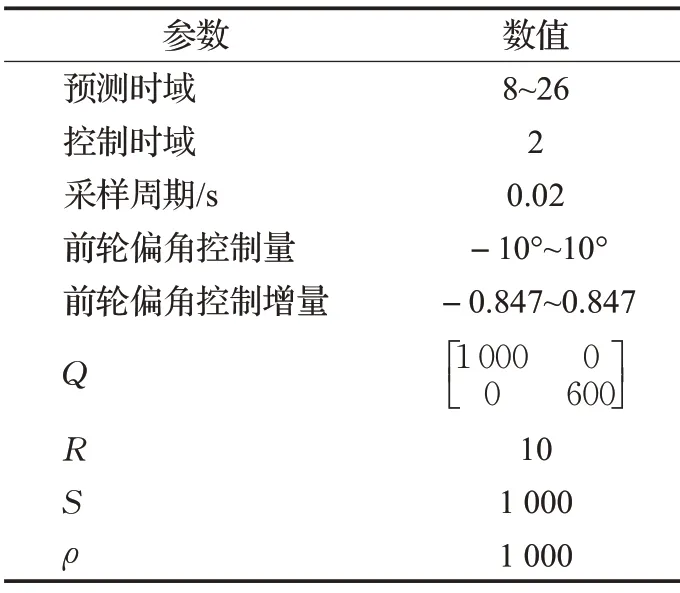
表2 控制器參數

在Carsim 軟件中設置路面附著系數為0.2，速度設置為36 km/h，控制器中預測時域設置為8。下面對添加側偏角約束的MPC控制器和未添加側偏角約束的MPC控制器分別進行軌跡跟蹤控制測試，仿真結果如圖4。

在上面的仿真結果中，根據圖4（a）和圖4（b）可知，控制器添加側偏角約束能夠有效提升車輛軌跡跟蹤的精度，其中未添加側偏角約束的最大橫向位置偏差為0.386 3 m，而添加了側偏角約束的最大橫向位置偏差為0.180 2 m。根據圖4（c）可知添加側偏角約束能夠有效提升車輛的行駛穩定性，其中未添加側偏角約束的最大質心側偏角和橫擺角速度分別為3.390 9°和14.081 4（°）/s，而添加了側偏角約束的最大質心側偏角和橫擺角速度分別為0.729 5°和8.027 9（°）/s。綜上所述控制器添加側偏角約束可以有效提高車輛軌跡跟蹤控制的行駛穩定性。

2.3 Hp 控制器的設計

2.3.1 Hp 對軌跡跟蹤控制的影響

預測時域作為MPC 的重要參數之一，表示控制器對未來狀態的預測程度。若車速一定時，由式（8）以及式（9）中的第一項可知，當Hp較大時，控制器可以預測較遠的距離，但會產生較大的誤差，降低軌跡跟蹤精度；當Hp較小時，在文獻[17]提出車輛轉向輪的轉向角速度約束的影響下，車輛又會因無法及時轉向而造成軌跡跟蹤失敗。所以不同的預測時域產生的控制效果不同。

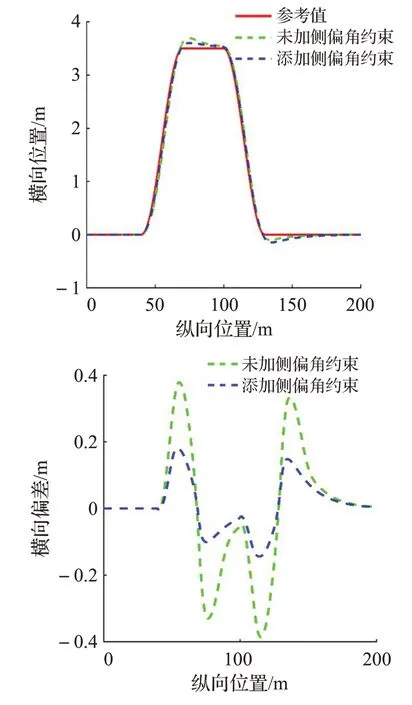
圖4（a）橫向位置和橫向偏差

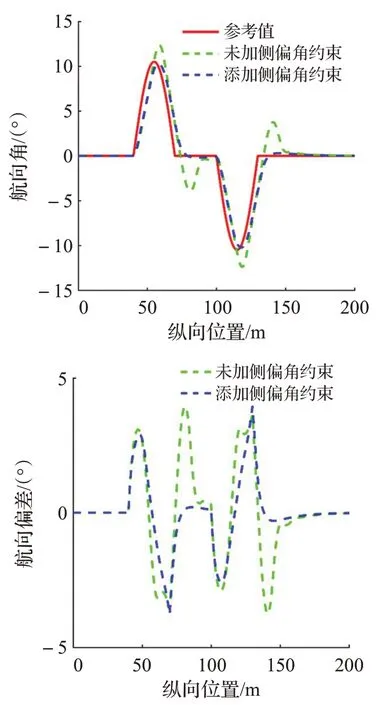
圖4（b）航向角和航向偏差

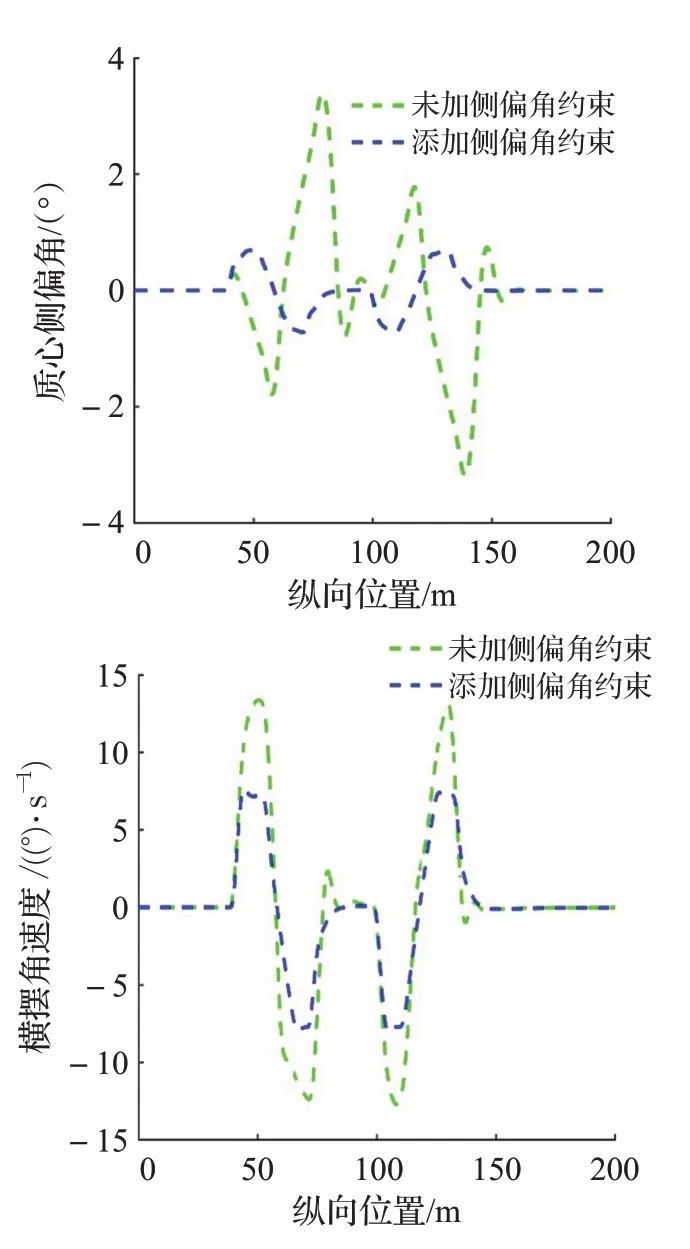
圖4（c）質心側偏角和橫擺角速度

下面在添加側偏角約束的基礎上，分析不同恒定速度下Hp取不同的值對軌跡跟蹤控制的影響。通過CarSim和MATLAB/Simulink聯合仿真進行了四組定速下不同Hp的軌跡跟蹤效果的測試，其中Hp也采用了四組。

（1）試驗一：36 km/h 下Hp取4 組不同定值的軌跡跟蹤。

在試驗一的仿真結果中，由圖5（c）可知，車速為36 km/h時，Hp取不同定值時軌跡跟蹤控制器操作穩定性均較為良好。但隨著Hp的增大，軌跡跟蹤的精確性隨之降低。由圖5（a）、圖5（b）可知，Hp=8 時，橫向偏差和航向偏差最小，Hp=26 時，橫向偏差和航向偏差最大。

圖5（a）36 km/h下的橫向位置和橫向偏差

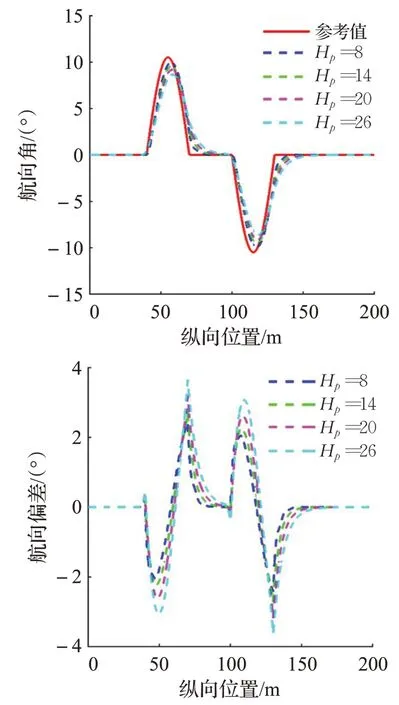
圖5（b）36 km/h下的航向角和航向偏差

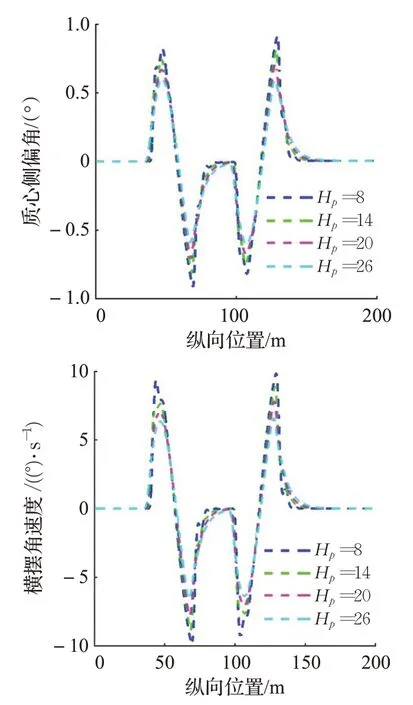
圖5（c）36 km/h下的質心側偏角和橫擺角速度

同理，分別進行72 km/h、90 km/h、108 km/h 下Hp取不同定值的軌跡跟蹤。

（2）試驗二：72 km/h 下Hp取4 組不同定值的軌跡跟蹤，跟蹤情況見表3。

表3 試驗二跟蹤情況

在試驗二的仿真結果中，車速為72 km/h時，Hp=8時，雖然橫向偏差和航向偏差最小，但質心側偏角和橫擺角速度的數值最大，說明有明顯抖動，軌跡跟蹤控制器操作穩定性較差。Hp=20 和Hp=26 時，雖然質心側偏角和橫擺角速度較小，但軌跡跟蹤的核心參數最大橫向偏差較大。而Hp=14 時，雖然橫向偏差相較Hp=8來講要大，但在可接受范圍內，且操作穩定性良好。

（3）試驗三：90 km/h 下Hp取4 組不同定值的軌跡跟蹤，跟蹤情況見表4。

表4 試驗三跟蹤情況

在試驗三的仿真結果中，當車速為90 km/h 時，Hp=8 和Hp=14 時，軌跡跟蹤失敗。Hp=20 和Hp=26時，質心側偏角和橫擺角速度相差不大，都有良好行駛穩定性，但Hp=20 時，軌跡跟蹤的核心參數最大橫向偏差最小，說明與參考軌跡的誤差更小，有更好的跟蹤精確性。

（4）試驗四：108 km/h下Hp取4組不同定值的軌跡跟蹤，跟蹤情況見表5。

表5 試驗四跟蹤情況

在試驗四的仿真結果中，車速為108 km/h 時，由仿真結果可知，Hp分別為8、14、20 時軌跡跟蹤失敗。而Hp=26 時，有良好的跟蹤精確性和行駛穩定性。

綜上所述，綜合考慮跟蹤精確性和行駛穩定性，可以得出結論低速時采用較小的Hp，而高速情況下采用較大的Hp有良好的跟蹤精確性和行駛穩定性。這是因為在模型預測算法中，當Hp較大時，控制器會考慮更多的未來軌跡趨勢變化，造成跟蹤精度下降。

2.3.2 Hp 控制器的設計

通過上一節的試驗，可知低速工況下，控制器應采用較小的Hp，高速工況下，控制器應采用較大的Hp。然而在軌跡跟蹤過程中，行駛工況有時會有變速的要求，那么此時控制器若采用固定的Hp將會無法滿足低速、高速、變速的行駛工況。

因此，下面將設計Hp的控制器，能夠根據車速度的變化，實時產生Hp。

根據上一節的試驗分析，下面根據4組速度對應的Hp，設計變Hp控制器，如表6所示。

表6 不同速度對應的Hp

具體控制規律如式（14）所示，是通過表6選取的四組數據進行三次多項式擬合得到。圖6 為不同速度對應的Hp。

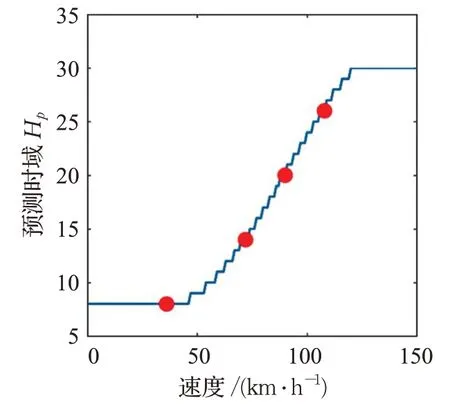
圖6 不同速度對應的Hp

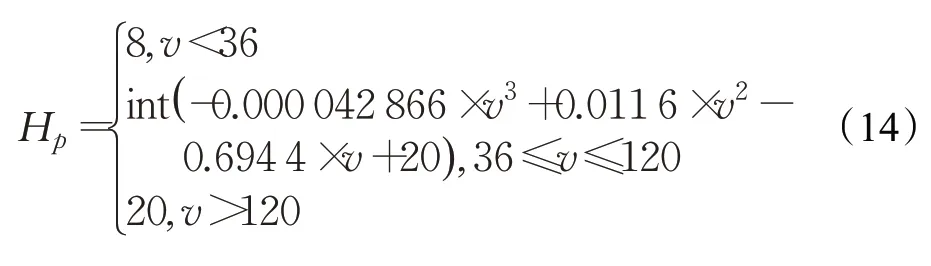
3 仿真分析

前面驗證了添加側偏角約束可以提高車輛在低附著路面軌跡跟蹤的精度與行駛穩定性，以及分析了不同速度下Hp取不同值對軌跡跟蹤控制的影響。在添加側偏角約束的基礎上結合變Hp控制器，共同構成了自適應MPC軌跡跟蹤控制器，下面對自適應MPC軌跡跟蹤控制器在變速且低附著環境下進行仿真分析。通過CarSim 和MATLAB/Simulink 搭建聯合仿真平臺，地面附著系數設置為0.2，為了模擬變速環境，CarSim中設置為超車工況，超車工況速度變化如圖7 所示，車輛參數和控制器參數如表1和表2所示。

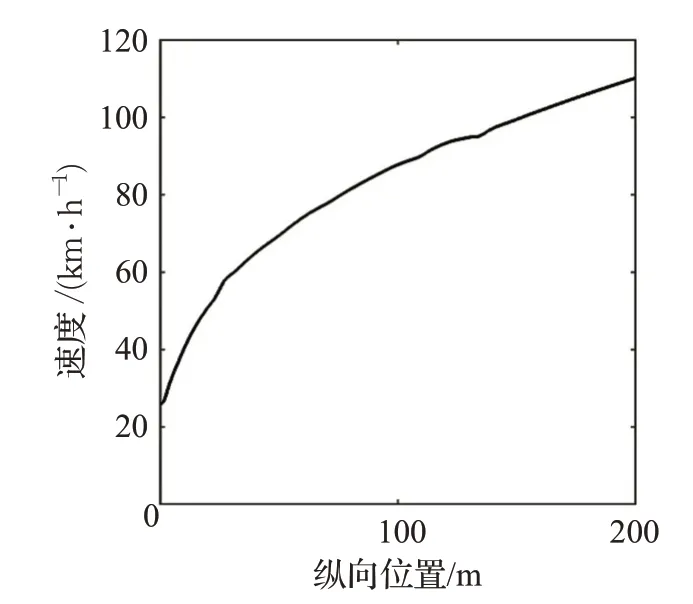
圖7 超車工況下速度的變化

在上面的仿真結果中，由圖8（a）知Hp分別為8、14、20 時軌跡跟蹤失敗。Hp=26 時最大橫向偏差為0.457 3 m，而自適應的MPC 控制器最大橫向偏差為0.385 6 m。由圖8（b）可知Hp=26 的最大航向偏差為10.771 1°，而自適應的MPC 控制器的最大航向偏差為2.236 4°。由圖8（c）可知Hp=26 最大質心側偏角和最大橫擺角速度分別為11.017 3°和39.867 0（°）/s，而自適應的MPC控制器最大質心側偏角和最大橫擺角速度分別為3.418 9°和26.653 1（°）/s。綜上所述，基于自適應的MPC控制器可以有效提高跟蹤精度和行駛穩定性。

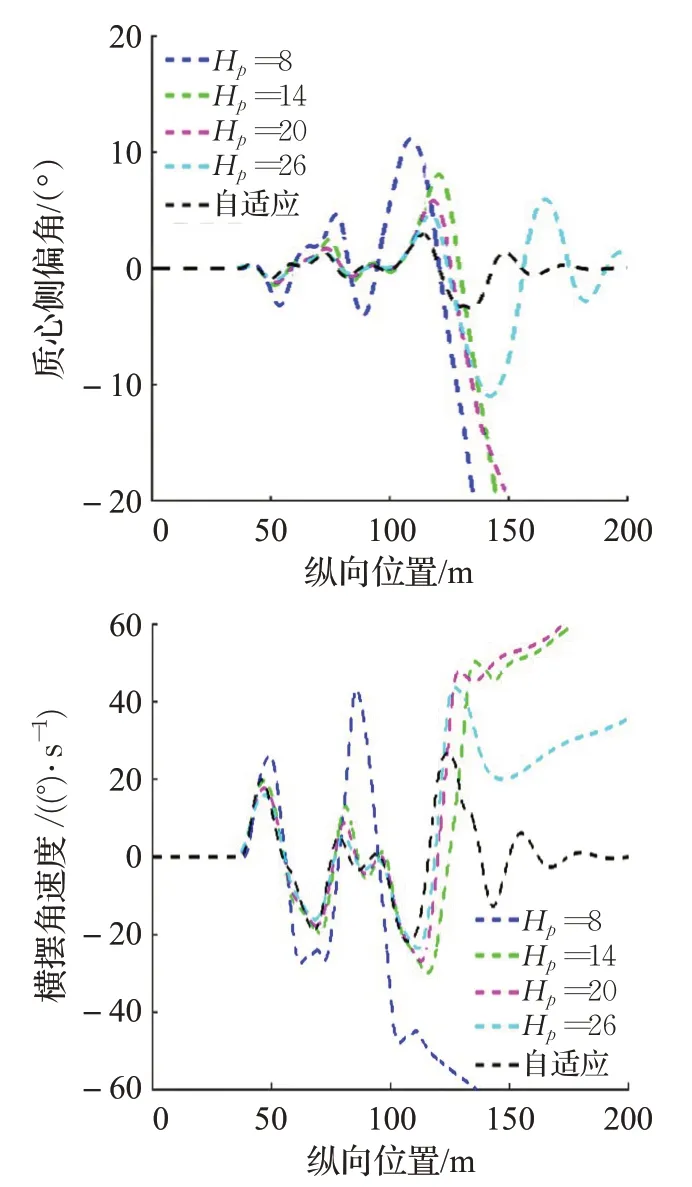
圖8（c） 超車工況下的質心側偏角和橫擺角速度

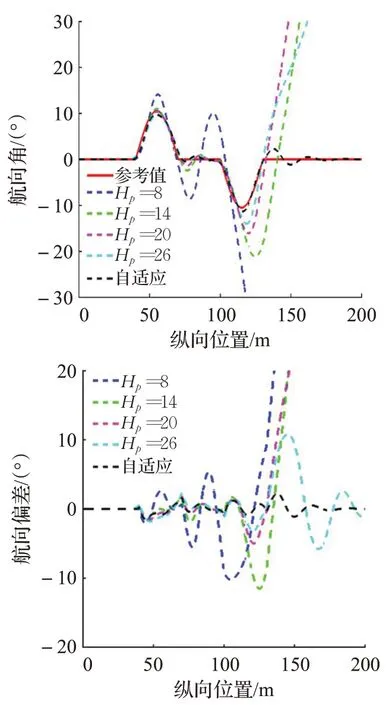
圖8（b） 超車工況下的航向角和航向偏差

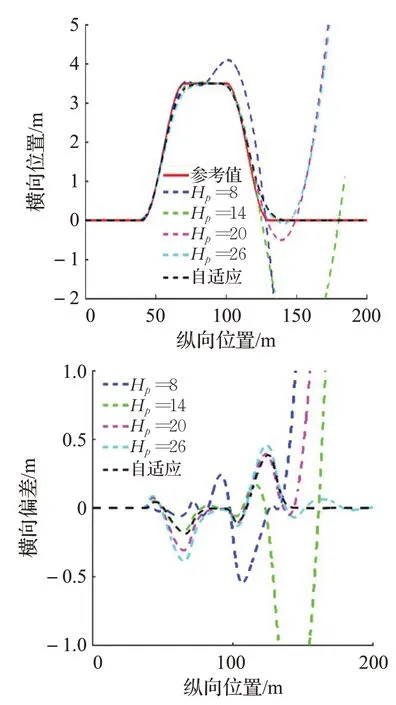
圖8（a） 超車工況下的橫向位置和橫向偏差

4 結論

本文研究了車輛在低附著且變速的環境下軌跡跟蹤控制問題。以車輛動力學模型為基礎，設計了自適應的MPC控制器，分別由添加側偏角的MPC控制器和變Hp控制器組成。通過MATLAB/Simulink 和Carsim 聯合仿真，所得結論如下：

（1）仿真數據表明，添加側偏角使得質心側偏角最大偏差減小了2.661 4°，橫擺角速度最大偏差減小了6.053 6（°）/s，有效提高車輛行駛的穩定性。

（2）采用自適應的MPC 控制器，相比無法根據車速更新Hp的控制器，使得最大航向偏差減小了8.534 7°，質心側偏角減小了7.598 4°，橫擺角速度減小了13.215 7（°）/s，有效提高了軌跡跟蹤精度和行駛穩定性。