巧用板貼，讓數(shù)學思考有“跡”可循

衡華麗

【摘 要】當下越來越多的教師依賴多媒體課件進行數(shù)學教學。課件固然直觀、便捷，但不利于針對課堂生成進行靈活的二度設計，更不能直接展示學生數(shù)學思考的過程。教師應當以生為本，適當靈活地運用可移動板貼，于課堂教學中多呈現(xiàn)學生樸素的數(shù)學思考。

【關鍵詞】以生為本 移動板貼 教學手段 數(shù)學思考

隨著信息技術的迅猛發(fā)展，網(wǎng)絡上各類網(wǎng)站如雨后春筍般強勢崛起，電腦制作的課件以其直觀、生動、便捷的優(yōu)勢迅速取代傳統(tǒng)的小黑板板書和實物教學。教師們大力追捧各類制作精美的課件，一度淪為課件的播放者，而學生則成了課件的欣賞者。

相較于低年段的數(shù)學學習，小學四、五年級的數(shù)學課堂知識容量更大，對學生的數(shù)學思維能力要求較高，需要學生對所學知識進行數(shù)學思考和自主建構。新課標指出：“教師是數(shù)學學習的組織者、引導者、合作者。”“教學活動是師生積極參與、交往互動、共同發(fā)展的過程。”課件的稍縱即逝很難在學生腦海中留下深刻的記憶，不利于學生數(shù)學思維的發(fā)展。同時，課件在課前已經(jīng)制作完成，很難根據(jù)課堂生成進行二度設計。

如何彌補這樣的不足？通過實踐，筆者發(fā)現(xiàn)用幾張活動板貼就能靈活地因“課”制宜。以前，活動板貼多出自教師之手，課前用來寫上板書，以節(jié)省上課時間。但是現(xiàn)在越來越多的教師把“粉筆”遞給學生，讓學生們書寫自己的思考過程，讓他們的數(shù)學思考有“跡”可循。

一、他山之石可攻“玉”——自學教學時巧用板貼

概念課教學中，大部分教師都是課前進行充分預設，將知識點一一羅列，以供學生識記、比較和理解，即使采取小組合作的方式，交流時的范圍仍然是在一個小小的圈子里。此時，教師可以巧用板貼靈活地利用課堂生成資源進行教學，將“點”的思考匯成“面”的交流。

（一）問一得三——適時引領

在課堂教學中，教師不僅要重視“大問題”教學，還要在每個板塊教學中啟發(fā)學生從數(shù)學角度去發(fā)現(xiàn)、提出、分析和解決問題，從而不斷提升學習力。

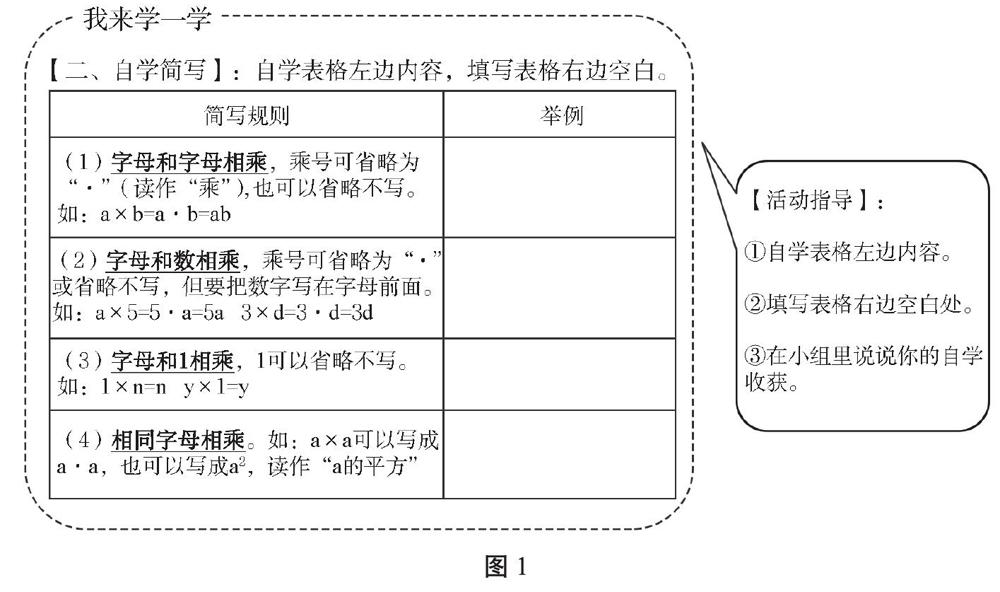
以蘇教版五年級上冊第八單元《用字母表示數(shù)》一課中的自學簡寫規(guī)則為例：

出示活動單的“我來學一學”，自學左邊簡寫規(guī)則并在右邊再嘗試舉例并在小組內交流。

學生舉例時，教師巡視各組，留意四類簡寫規(guī)則的舉例情況。選取有代表性的例子讓學生自己板書在板貼上，并貼在黑板上（無序的）。

教師和學生將板貼一一對照四類簡寫規(guī)則，指出每一條的注意點，并相機板貼出四條簡寫規(guī)則。

師：通過自學，你都看懂了什么？

生1：字母和具體的數(shù)相乘時，乘號可以簡寫為一個圓點或者干脆不要。

生2：省略乘號時，具體的數(shù)寫在字母前面。

師：可乘、可點、可不寫;數(shù)字放在字母前。

師：還有什么發(fā)現(xiàn)？

生1：1×a就可以簡寫為a。

生2：1和某個字母相乘，就可直接簡寫為那個字母。

師：好極了！還看懂了什么？

生1：a×a可以簡寫成a·a或a2，讀作“a的平方”。

生2：同樣的兩個字母相乘，不僅乘號可以簡寫為一個點或者省略不寫，還有更簡單的寫法，只寫一個字母，然后在字母的右上角寫一個小小的2，就表示兩個同樣的字母相乘，讀作“a的平方”。

師：與1相乘1省略;同數(shù)相乘即平方。

這個環(huán)節(jié)教師給予學生充分的自學時間。學生自學后讓學生自己當小老師給大家講講簡寫法則、自學收獲以及注意點。學生在當小老師的過程中鍛煉了語言表達能力和歸納能力，同時又成了課堂的主人。

（二）一題多用——適當拓展

教學中不可一味地“就題論題”，要合理安排，適當拓展，發(fā)揮題目中潛在的使用價值。仍以《用字母表示數(shù)》一課的教學為例。教師提問：黑板上哪些含有字母的式子可以簡寫呢？選一個試試看。學生自主選擇板貼上的算式進行簡寫。

教學簡寫規(guī)則前，學生所寫算式，除了乘法運算還有加法、減法和有小括號的算式。面對這些算式，學生的改寫熱情更高。這樣利用“變式”和“反例”來促進學生對新知的理解，從而達到理想的課堂教學效果。

二、三人行，必有我“師”——策略教學時巧用板貼

解決問題的策略教學課一直是每一個學期教學內容的重點及難點。何為“策略”？策略源于方法，高于方法，更多體現(xiàn)了使用者的智慧與謀略。對于學生，學習的不僅僅是解一類題的方法，更重要的是在學習活動中獨立思考，體會數(shù)學的基本思想和思維方式。

（一）強化內涵，提升課堂思維生長

教材既是教與學的重要依據(jù)，又是教師教學的主要資源。教師尋找教材的核心和精髓是有效教學的重中之重。

以蘇教版五年級下冊《解決問題的策略（轉化）》為例。

教學設計分為三個層次：

1.體會轉化的策略：比較課本例題兩個不規(guī)則的圖形面積的大小。

2.應用轉化的策略：分為“講故事”“巧拼圖”“不可能”“善計算”4個部分的練習，學生自主選擇。

（1）講故事：曹沖稱象、愛迪生測量燈泡、阿基米德測量皇冠。

（2）巧拼圖：用分數(shù)表示各圖中的涂色部分，并在小組里說說你是怎么想的。

（3）不可能：800 （ ） + 200（ ）= 1 （ ），11 = 3 ，半斤=8兩。

（4）善計算：讓學生在黑板貼上自己出題給其余同學寫。（要求解題時用到轉化的策略）

3.全課總結，深化策略：通過本節(jié)課的研究和探索，我們知道了解決問題要：化（ ）為（ ）。（再次讓學生在小組內討論后在板貼上寫上貼于黑板）

上述設計從數(shù)學表達、圖形與幾何、數(shù)與代數(shù)等方面著手，避免落入學完策略后變成只做題的窠臼。讓學生的所思所想落筆于板貼，在課堂中生根開花;讓學生的數(shù)學思考有“跡”可循。

（二）合理抽象，二度設計引發(fā)思維進階

小學生的思維是處于以形象思維為主，逐步地向以抽象思維為主過渡的階段。教師在教學時要引導學生以感知材料為基礎，能動地進行抽象思維。

以蘇教版四年級下冊《解決問題的策略（畫線段圖）》為例。

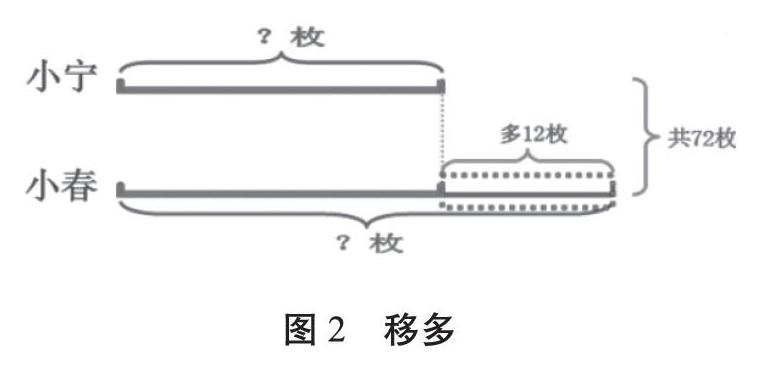
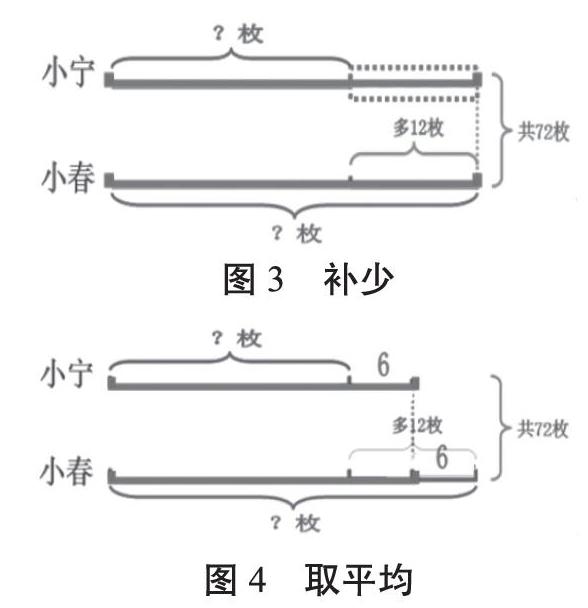
例題：小寧和小春共有郵票72枚，小春比小寧多12枚，兩人各有郵票多少枚？

這節(jié)課大多數(shù)教師會將三種畫圖情況在課件上做好，之后通過學生的回答來出示：

還有一部分教師會讓學生先討論，再分別在黑板上畫線段圖之后解答。相比之下，第一種教學方式過于快速，學生即使理解了圖意，但自己不能完整規(guī)范地畫出線段圖。第二種教學方式考慮到了要以學生為主，也能培養(yǎng)學生的作圖能力，但是花在尋找不同解法上的時間較長。

權衡之下，教師可以為每組學生準備大片的板貼，小組內討論，再由學生代表獨立畫圖，教師巡視后選擇不同解法的板貼展示在黑板上，然后請學生代表講解，這樣省時又高效。“小老師”在表述時有“圖”可講，有話可說，更能清晰地表達思考過程。對于第三種較難理解的算法，學生也能在圖上進行二次設計，可謂一舉多得。

三、溫故知新可為“師”——復習教學時巧用板貼

復習課對學生系統(tǒng)梳理知識點、扎實學好數(shù)學極為重要。要真正上好復習課并非易事，如果不精心設計，就達不到預期的效果。例如，順次復習、重復舊課，這樣既浪費時間，又會使學生感到索然無味;不分主次、學生重復練習，會使學生學無所得，降低學習數(shù)學的興趣;把知識點簡單羅列不加整理，使學生茫然而無頭緒。

（一）關注學生的學習經(jīng)驗

學生的數(shù)學學習是一個自主建構的過程，如果教師能夠了解學生已有的生活經(jīng)驗、活動經(jīng)驗、數(shù)學經(jīng)驗，讓學生借助已有的經(jīng)驗去研究新的知識，就會不斷收獲成功。

以《兩三位數(shù)除以兩位數(shù)》這節(jié)復習課為例。

從“點”出發(fā)，回顧已知。（1）回想：這一單元中你學到了什么？（2）展示匯報：誰來給大家介紹介紹。

學生匯報，教師在方形板貼上依次無序地板書：口算、估算、筆算、連除的規(guī)律、商不變的規(guī)律、商變化的規(guī)律，并明確每一項的注意點。

（二）尊重學生的個性

學生個體之間是存在差異性的。有的教師在教學中自己對知識點進行加工和梳理，看似有章可循的知識框架，實則是教師自己的知識建構。這樣的知識框架反而會“框”住學生的思維，不利于學生的自主建構。以《兩三位數(shù)除以兩位數(shù)》這節(jié)復習課為例。本節(jié)課教師可以利用板貼，將課堂主動權還給學生。

沿“線”梳理，形成關聯(lián)。（1）提出任務：剛才同學們提到這么多個知識點，你能理一理，讓它們變得有條理些嗎？（2）這里有一個三位數(shù)除以兩位數(shù)的式子，但是被除數(shù)和除數(shù)都用小方格表示，不知道具體的數(shù)，你能筆算嗎？（板書見圖5）

這節(jié)課沒有使用電腦課件，只借助移動板貼，學生獨立進行知識的建構。即使自主構建時分類方法有所不同，幸運的是，學生頭腦中抽象的分類都在這幾片小小的板貼移動間展現(xiàn)得淋漓盡致。抽象的知識在直觀可移動的圖片中游走，學生的數(shù)學思考在板貼的排列間盡情展現(xiàn)。

在數(shù)學教學中，教師要靈活地選用教學手段。適當?shù)厍捎冒遒N，把學習的主動權還給學生。讓學生在數(shù)學課堂上體驗從“經(jīng)歷了”到“發(fā)現(xiàn)了”、從“正在思考”到“越來越會思考”的學習歷程。真正打開學生的思維之門，讓學生的數(shù)學思考有“跡”可循。

【參考文獻】

[1]郭思樂.教育激揚生命：再論教育走向生本[M].北京：人民教育出版社 ，2007.

[2]皮連生.學與教的心理學[M].上海：華東師范大學出版社，2009.

[3]李烈.我教小學數(shù)學[M].北京：人民教育出版社，2003.