需求和回收不確定的閉環供應鏈渠道結構選擇

張 盟，郭健全

（1.上海理工大學管理學院，上海 200093；2.上海理工大學上海-漢堡國際工程學院，上海 200093）

0 引言

隨著資源浪費和環境污染日益嚴重，可持續發展受到廣泛關注［1］。回收再制造作為閉環供應鏈的重要部分，能夠延長廢舊品的使用壽命，緩解環境污染，降低生產成本，所以企業越來越重視回收再制造［2］。然而，閉環供應鏈系統更加復雜：如在不確定環境下，企業如何選擇最優渠道結構并制定最優生產決策等，使閉環供應鏈面臨諸多挑戰［3］。

再制造閉環供應鏈面臨更多不確定因素，市場需求、回收率、回收質量和再制造成本等主要不確定因素增加了企業在回收、生產和銷售等決策上的難度［4］。市場需求的變化極大地影響企業的生產決策，不確定回收質量同時影響著回收率和再制造成本，因此需求和回收質量是重要的不確定因素［4］。Kim 等［5］考慮需求不確定建立了非線性規劃模型；Ma 等［6］研究了需求不確定對價格的影響；Xiong 等［7］基于回收質量不確定研究了動態定價對總利潤的影響；Heydari 等［8］在回收質量不確定下建立收益共享機制來分擔不確定風險。上述文獻單獨討論了整體需求和回收質量不確定性，然而現實市場需求往往劃分為新產品和再制造品［9］，且經常同時出現需求和回收質量不確定，基于此，本文同時探討不確定需求（新產品和再制造品需求）和回收品質量對最優決策的影響。

針對求解不確定問題的方法，Farrokh 等［10］采用隨機規劃法處理需求和成本不確定問題；Kim等［5］運用魯棒優化解決需求不確定問題；Tsao 等［11］運用模糊機會約束規劃法解決需求不確定問題。隨機規劃需要足夠多的統計數據支持［10］；魯棒優化過于注重置信水平，導致結果較為保守［5］；模糊機會約束規劃法既可以解決缺少精確數值的問題，又能夠避免結果過于保守［11］。因此，本文采用模糊機會約束規劃法解決新產品和再制造品需求不確定問題。

政府補貼對回收再制造活動具有激勵作用。Wang 等［12］研究了補貼制造商對經濟效益和回收數量的影響；Sun 等［13］基于補貼制造商建立了進化博弈論模型；Li 等［14］探討了政府消費補貼對社會福利和環境效應的影響；Bian 等［15］對比研究了補貼消費者和制造商對碳減排的影響。上述文獻單獨討論了補貼制造商或消費者，未考慮回收質量對補貼額的影響，本文將回收質量考慮到政府補貼中，研究政府對制造商和消費者的差別權重補貼對最優決策的影響。

針對銷售渠道選擇問題，Li 等［16］采用直銷渠道并研究了設計投資對均衡決策的影響；Xie等［17］基于雙渠道銷售研究了分級回收對緩解低質量回收的影響；Alamdar等［18］在零售商分銷模式下考慮銷售努力建立了六種博弈論模型；Xie等［19］研究了雙渠道環境下閉環供應鏈的契約協調。上述文獻只涉及單一銷售渠道結構，直銷和分銷在不同情況下各有優劣，直銷節省了產品庫存成本，但是隨著直銷平臺費用的增加，相較于分銷顯示出劣勢，分銷節省了直銷平臺費用，但是隨著產品庫存成本的增加，相較于直銷顯示出劣勢［20］。因此，本文建立了四種銷售渠道結構系統總利潤模型，研究了不同情況下銷售渠道結構的最優選擇問題。

綜上所述，本文以閉環供應鏈系統總利潤最大化為目標，在市場需求和回收品質量水平不確定環境下考慮政府差別權重補貼和直銷平臺費用，構建了四種銷售渠道結構閉環供應鏈系統總利潤模型。運用模糊機會約束規劃法解決新產品和再制造品需求不確定問題，并采用粒子群優化（Particle Swarm Optimization，PSO）算法和遺傳算法（Genetic Algorithm，GA）對比求解模型算例。本研究可為企業在不確定環境下制定最優回收、生產和銷售策略提供參考，同時為企業在不確定環境下選擇最優銷售渠道結構提供借鑒。

1 模型構建

1.1 模型假設

1）在一個周期中原材料只采購一次［21］；

2）不考慮提前期、缺貨或過剩［22］；

3）單位再制造品利潤大于單位新產品利潤［22］；

4）回收品質量水平服從指數分布［3］；

5）政府實行差別權重補貼政策，消費者補貼權重為w，制造商補貼權重為1-w，0 ＜w＜1［23］。

1.2 符號說明

本文參數和決策變量的符號說明如表1和表2所示。

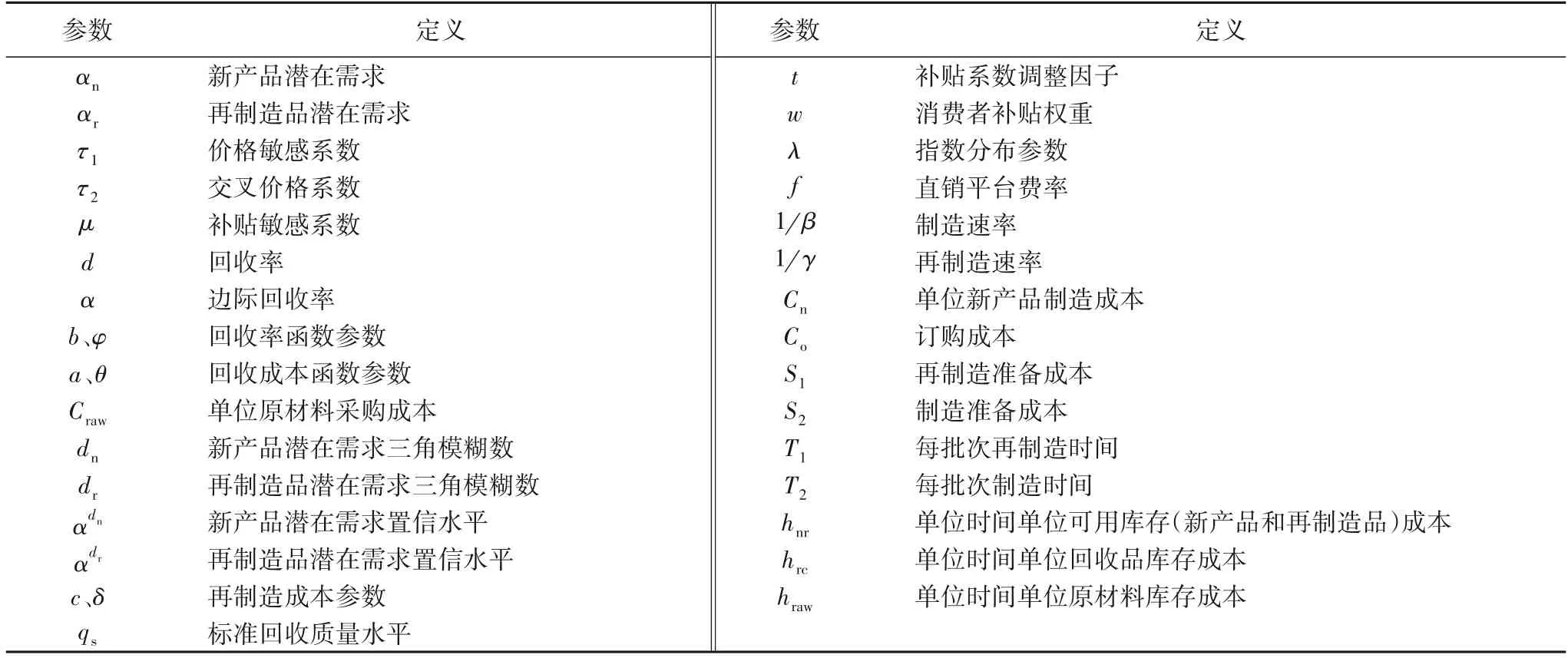
表1 參數符號說明Tab.1 Symbol description of parameters

表2 決策變量符號說明Tab.2 Symbol description of decision variables

1.3 函數構建

整體市場需求D包含新產品市場需求Dn和再制造品市場需求，函數為：

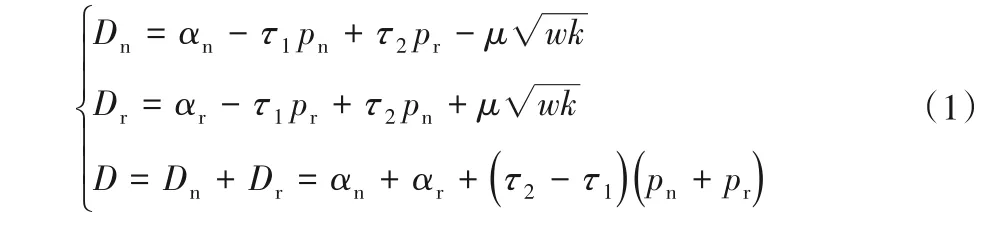
定義回收率d=αD，邊際回收率α=be-φq［1］（0 ≤q≤1，0 ≤b≤1）。q為回收品質量水平，且服從指數分布q～E(λ)，λ為指數分布參數，q的概率密度函數為：

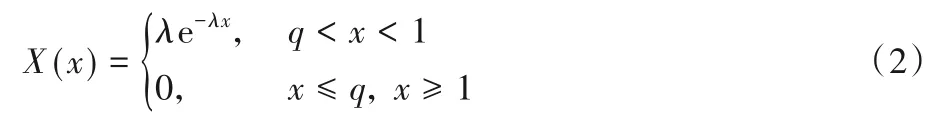
1.3.1 回收成本函數

定義回收成本比率p=ae-θ(1-x)［2］，a和θ為回收成本參數，0 ≤a≤1，p是單位回收成本與單位生產成本的比值。平均回收成本V1=d.Cn+Craw)E(p)，計算可得：

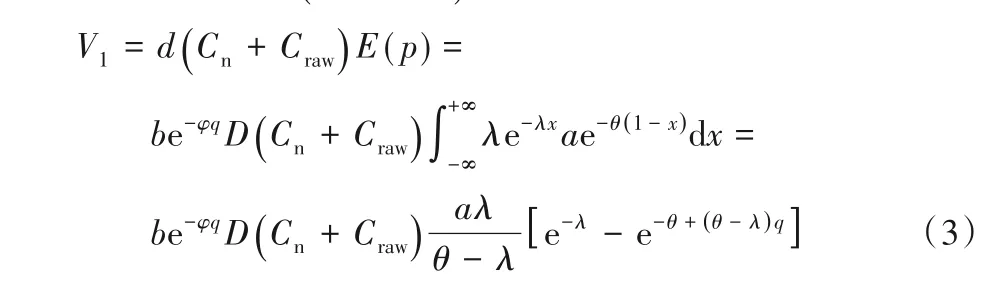
1.3.2 再制造成本函數

定義再制造成本比率j=ceδ()1-x［3］，c和δ為再制造成本參數，0 ≤c≤1，j是單位再制造成本與單位制造成本的比值，平均再制造成本V2=dCnE(j)，計算可得：

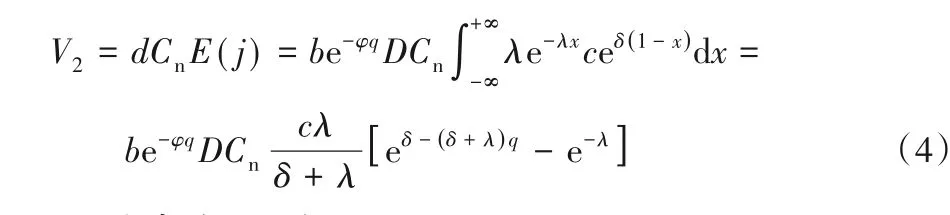
1.3.3 政府補貼函數

政府對制造商和消費者采取差別權重補貼政策。根據Guo 等［24］的研究，針對不同回收質量水平，單位再制造品補貼為k=則制造商總補貼額為：

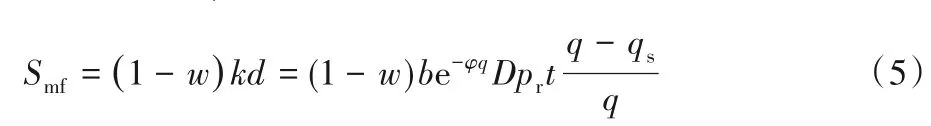
消費者購買再制造品的總補貼額為：

1.4 系統模型

制造商采購原材料用于新產品生產并回收廢舊品用于再制造活動，新產品和再制造品通過直銷或分銷渠道進行銷售，消費者從直銷/分銷渠道購買新產品或再制造品，并將廢舊品回收給制造商，政府對制造商和購買再制造品的消費者進行補貼，如圖1所示，整個過程形成物料循環流動。

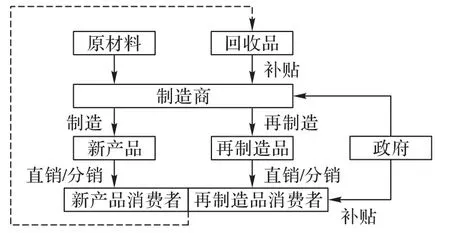
圖1 閉環供應鏈系統模型Fig.1 Closed-loop supply chain system model

四種渠道結構如表3所示：第1種渠道結構采用直銷渠道銷售兩種產品；第2 種渠道結構采用直銷渠道銷售新產品并采用分銷渠道銷售再制造品；第3 種渠道結構采用分銷渠道銷售新產品并采用直銷渠道銷售再制造品；第4 種渠道結道結構采用分銷渠道銷售兩種產品。

表3 四種不同渠道結構Tab.3 Four different channel structures

1.4.1 庫存水平

一個周期T包含l個制造期T2和m個再制造期T1，可得mDT1=dT，lDT2=DT-dT。庫存狀況如圖2 所示，再制造品和新產品庫存上升速度為回收品和原材料庫存下降速度為

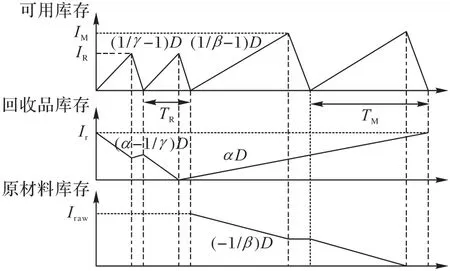
圖2 庫存狀況（以m=2，n=2為例）Fig.2 Inventory status（with m=2，n=2 for example）

經過推導可得最大再制造品庫存Ir、最大新產品庫存In、最大回收品庫存Irc和最大原材料庫存Iraw為：

1.4.2 平均庫存持有成本

再制造品和新產品平均庫存持有成本為Hr和Hn、回收品和原材料平均庫存持有成本為Hrc和Hraw，計算可得：

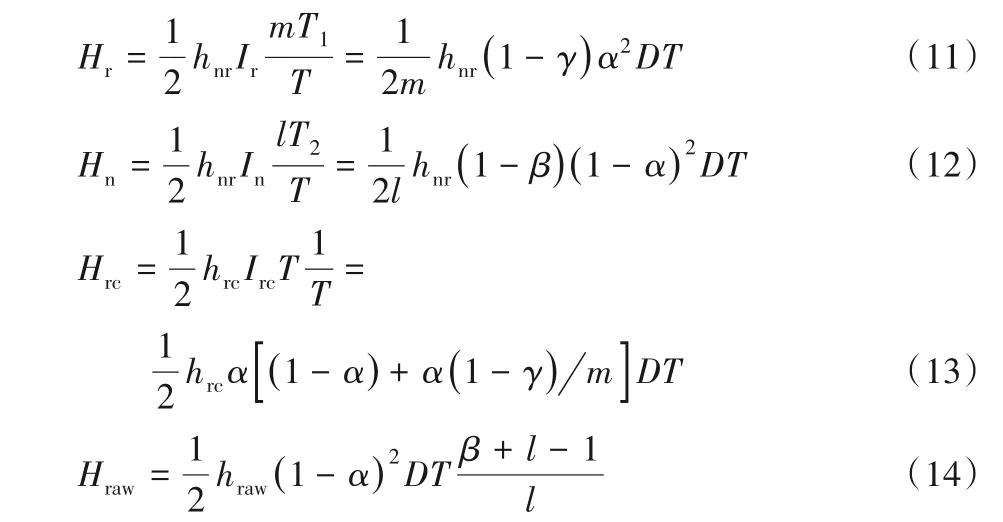
1.4.3 平均總利潤

制造成本指新產品生產成本；訂購成本指補充庫存成本；原材料持有成本指維護原材料的成本；生產準備成本包括制造和再制造準備成本。平均制造成本V3、平均訂購成本V4、平均原材料持有成本V5、平均生產準備成本V6計算可得：

直銷和分銷各有優劣，通過構建四種渠道結構系統平均總利潤模型，研究不同情況下銷售渠道結構的最優選擇問題。

模型一 新產品和再制造品均采用直銷渠道NSRS：

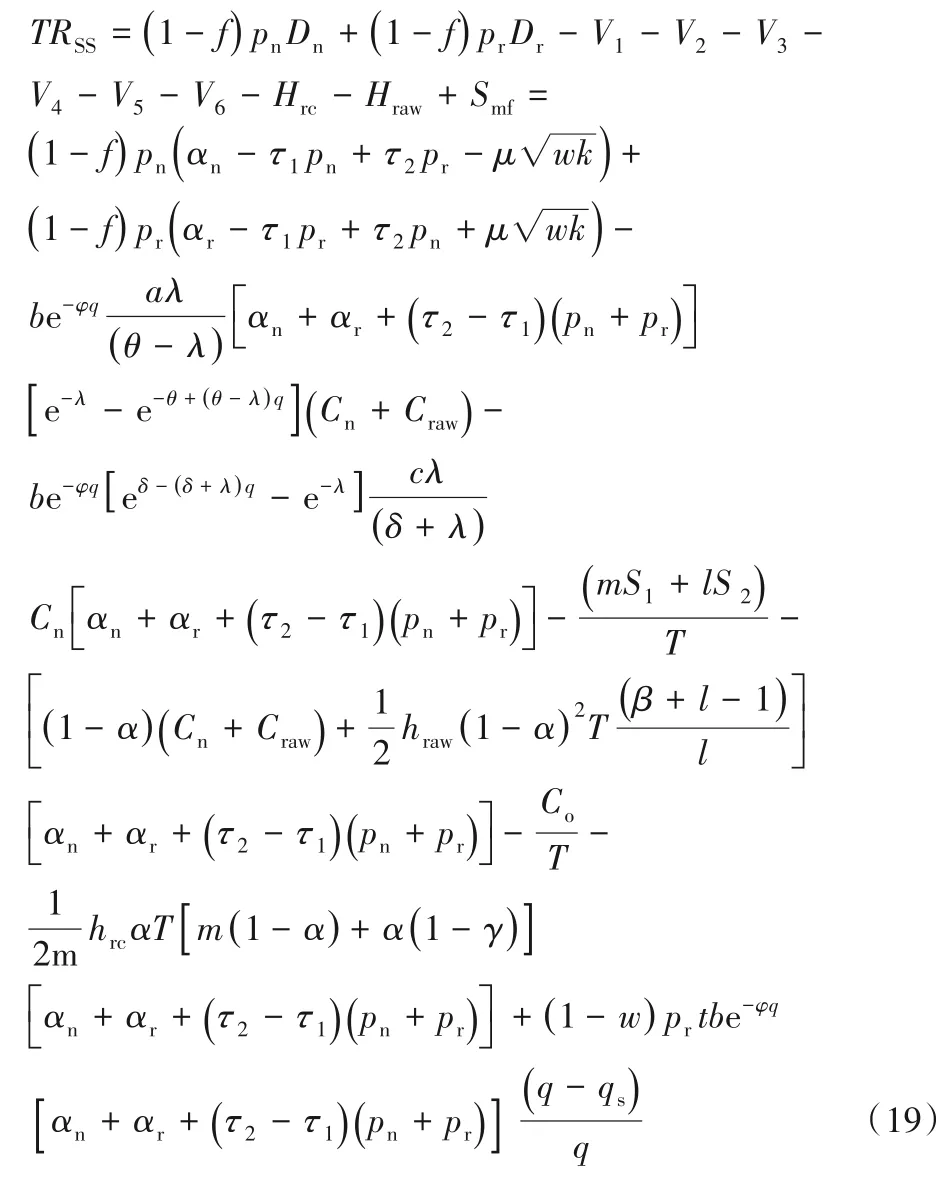
模型二 新產品采用直銷，再制造品采用分銷NSRL：

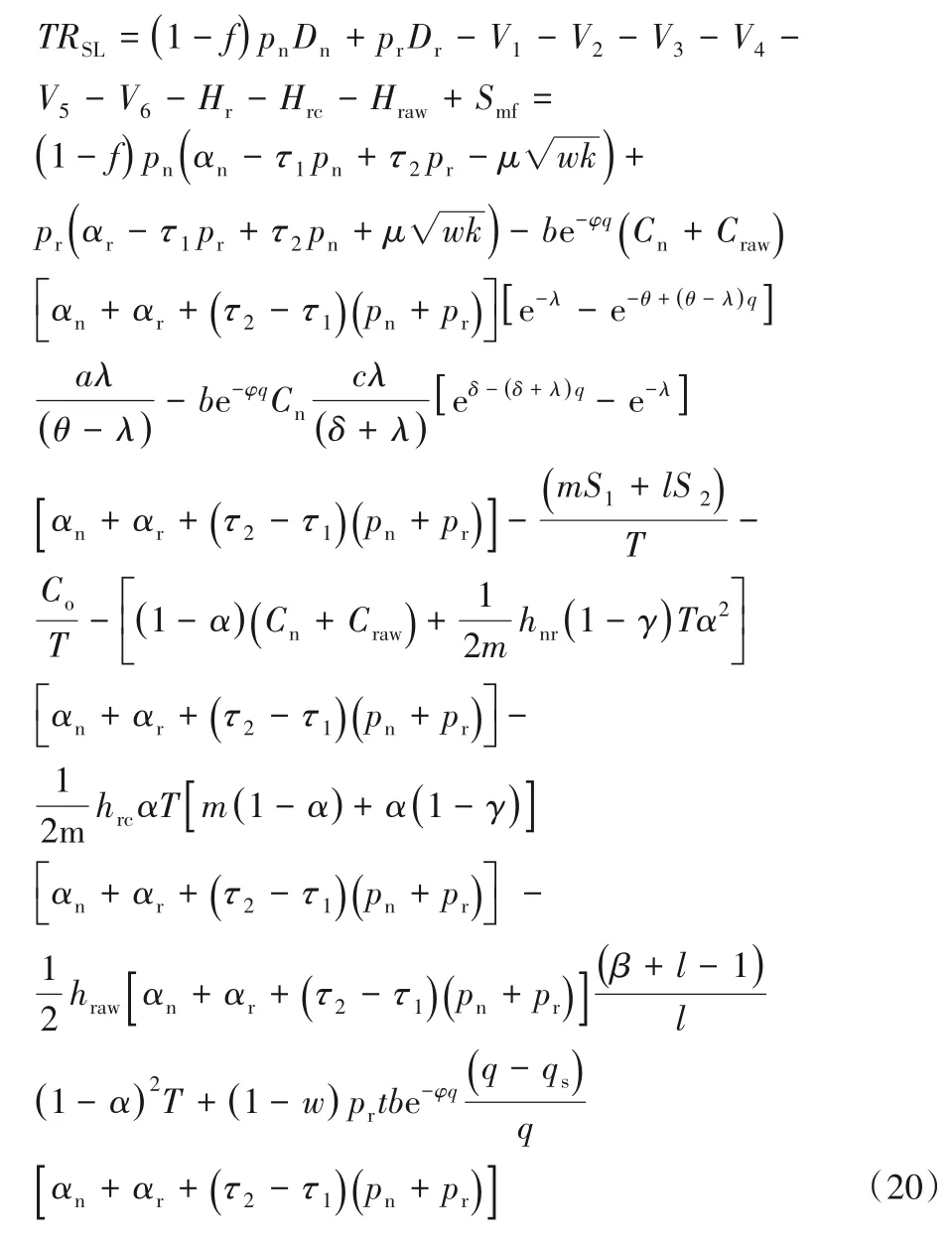
模型三 新產品采用分銷，再制造品采用直銷NLRS：

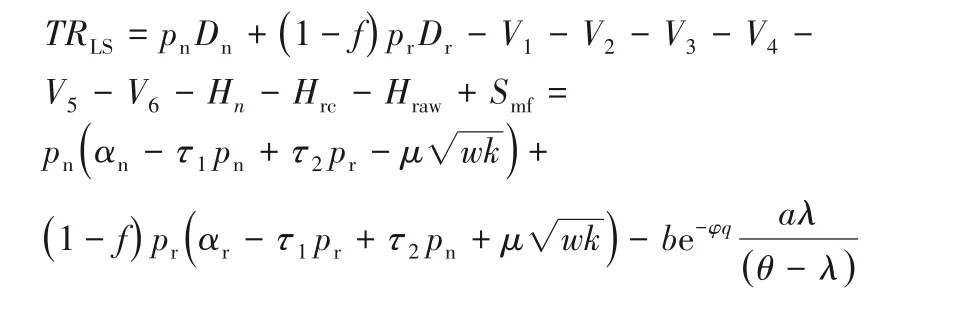
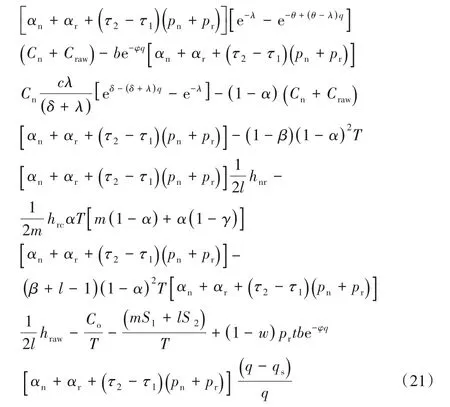
模型四 新產品和再制造品均采用分銷渠道NLRL：

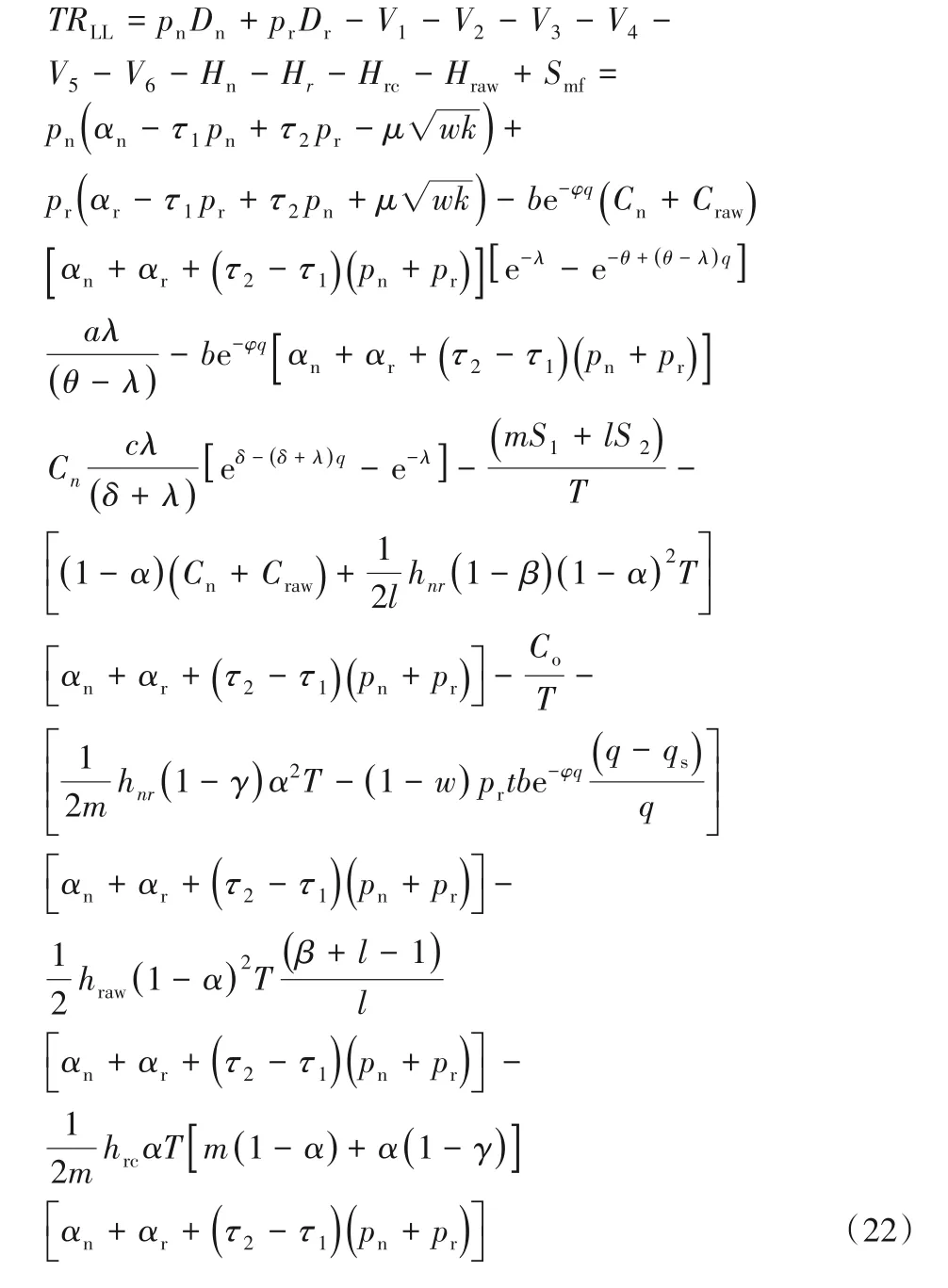
1.4.4 模糊機會約束清晰化

模糊機會約束規劃（Fuzzy Chance Constrained Programming，FCCP）法的主要思想是將模糊約束轉化為與之等價的確定式［11］。定義新產品和再制造品潛在需求模糊數為dn=(dn1，dn2，dn3)和dr=(dr1，dr2，dr3)，模糊隸屬函數為：

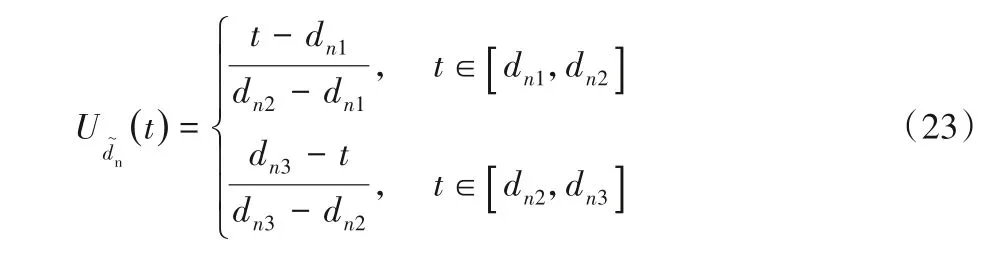
由模糊機會約束規劃法的清晰化定義及其引理可得：

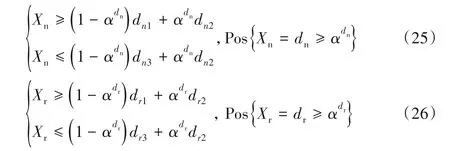
其中：Pos{·}表示{·}中事件成立的可能性。

2 算法設計

傳統優化方法求解具有連續/整數混合變量和不確定約束的非線性離散優化問題需要大量計算時間，元啟發式算法被認為是有效解決方式［24］，例如GA、PSO 算法、蟻群優化（Ant Clony Optimization，ACO）算 法、禁忌搜索（Tabu Search，TS）等。

已知研究大多采用GA 和/或PSO 算法獲得函數優化、選址與路徑規劃等問題的近似最優解，其中王心月等［3］驗證了GA 與PSO 算法求解非線性離散優化問題時可以獲得高質量解，Guo 等［24］采用PSO 算法與GA 對比求解函數優化問題，Soleimani等［25］通過GA與PSO算法驗證了相關模型的信度。

PSO 算法和GA 均是用于搜索近似最優解的元啟發式智能優化算法［26］，二者各有優劣：PSO 算法實現快，但易陷入局部最優；GA 能夠同時處理多個種群個體，降低陷入局部最優的風險，但效率相對較低［27］。

本文主要研究閉環供應鏈管理問題，對比使用PSO 算法和GA 是為了求得高質量的近似最優解，進一步驗證模型信度與算法效度。兩者迭代過程具有互補優勢，且相關研究采用兩種算法對比驗證了此類模型的信度，計算結果較好，其他如ACO 算法和人工蜂群（Artificial Bee Colony，ABC）算法等可能也可以解決該問題，在以后的研究中可以考慮。

2.1 粒子群優化算法

PSO 算法源于鳥群覓食行為的智能優化算法，在初始階段生成一批隨機解，通過不斷迭代尋找最優解［26］。因其操作簡單和易實現等特點，而被廣泛應用于物流網絡構建、路徑規劃等問題［28］。具體操作步驟如下：

1）隨機初始化粒子位置、速度和各項參數：本文粒子群規模為30，最大迭代次數為200，搜索空間維數為6。

2）根據適應度函數獲得粒子的適應度值：本文適應度函數為式（19）～（22）。

(4)環網柜處還需設置電壓互感器，根據安裝地電氣條件和安裝要求，選擇電壓互感器型號為JDZ9-10Q，高壓側電壓為10 kV，低壓側電壓100 V。絕緣性能優良、耐潮濕。

3）評估適應度值：根據歷史和當前適應度值，找出粒子當前最優位置pbest和整個粒子群最優位置gbest。

粒子i的第d維速度和位置更新公式為：

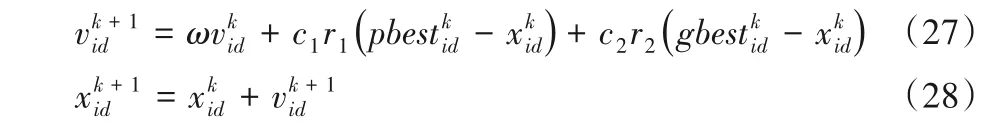
其中：c1和c2為加速常數；r1和r2為隨機數，取值范圍為［0，1］；ω是慣性權重。本文ω取0.729 8，c1=c2=2。

5）若達到終止條件（最大迭代次數），輸出最優解，否則返回步驟2）。

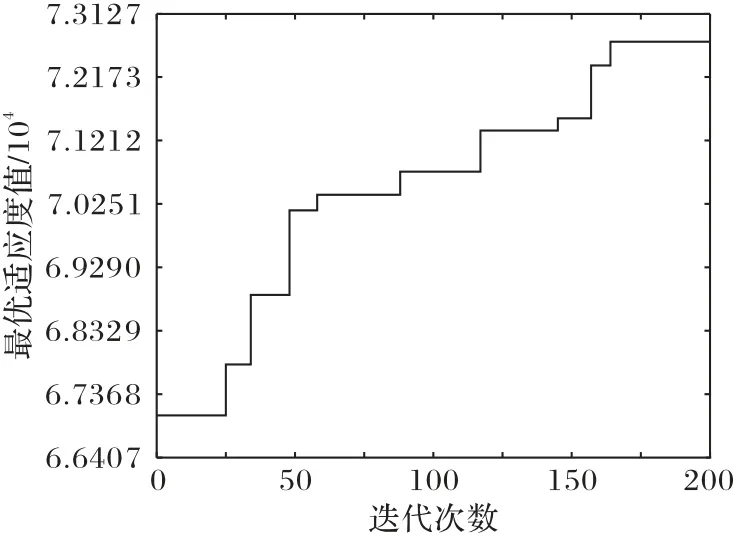
圖3 PSO的迭代收斂曲線Fig.3 Iterative convergence curve of PSO

2.2 遺傳算法

GA 是基于遺傳機制和自然選擇的智能優化算法，通過復制、交叉和變異使群體不斷進化，直到獲得最優解［27］。因其具有并行性、全局尋優能力、自動調整搜索方向等特點，被廣泛應用于物流網絡構建、車輛路徑規劃、函數優化等問題［29］。具體操作步驟如下：

1）染色體編碼與初始化。一條染色體對應問題的一個解，一個基因對應解的組成元素。本文染色體基因數為6，最大迭代次數為200，群體規模為40，交叉和變異概率為0.7 和0.03。本文采用二進制編碼，隨機產生0/1 初始種群，如表4所示。

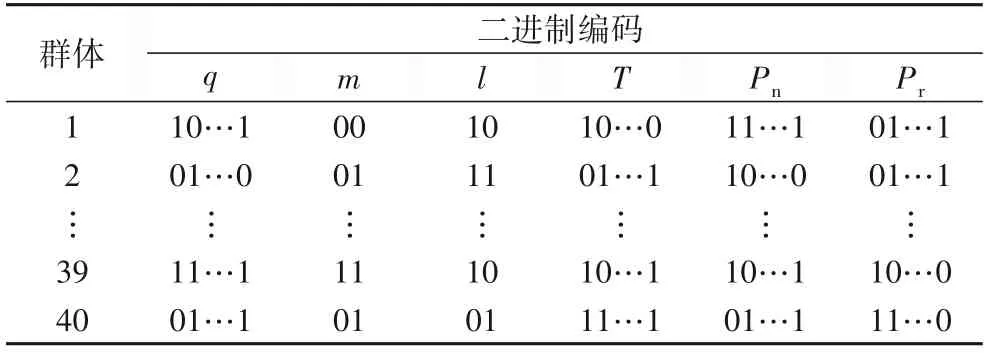
表4 GA的初始種群Tab.4 Initial population of GA

2）計算適應度值。根據適應度函數f(x)=計算適應度值，object分別為式（19）～（22）。

3）個體選擇。采用賭輪盤法進行個體選擇，目標函數值越大，染色體越容易被選上，被選擇的概率為：

4）交叉和變異。交叉變異過程如表5 所示，依據交叉和變異概率，隨機產生交叉和變異位置。

表5 GA的交叉、變異操作過程Tab.5 Cross and mutation process ofGA

5）若達到終止條件（最大迭代次數），輸出最優解，否則返回步驟2）。

3 算例分析

根據制造行業實際情況和相關文獻［1-2，24］研究，設置參數值：hnr=2，hrc=0.2，hraw=0.2，Cn=30，Craw=20，Co=1000，S1=1500，S2=1500，a=0.9，b=0.9，c=0.1，γ=0.6，β=0.5，φ=2，λ=1，τ1=3，τ2=2，qs=0.2，μ=80，t=0.9，w=0.4，f=0.3。本文采用數據集進行模擬運算，潛在需求三角模糊數如表6所示。

表6 潛在需求三角模糊數Tab.6 Potential demand triangle fuzzy numbers

3.1 不確定環境下的最優決策

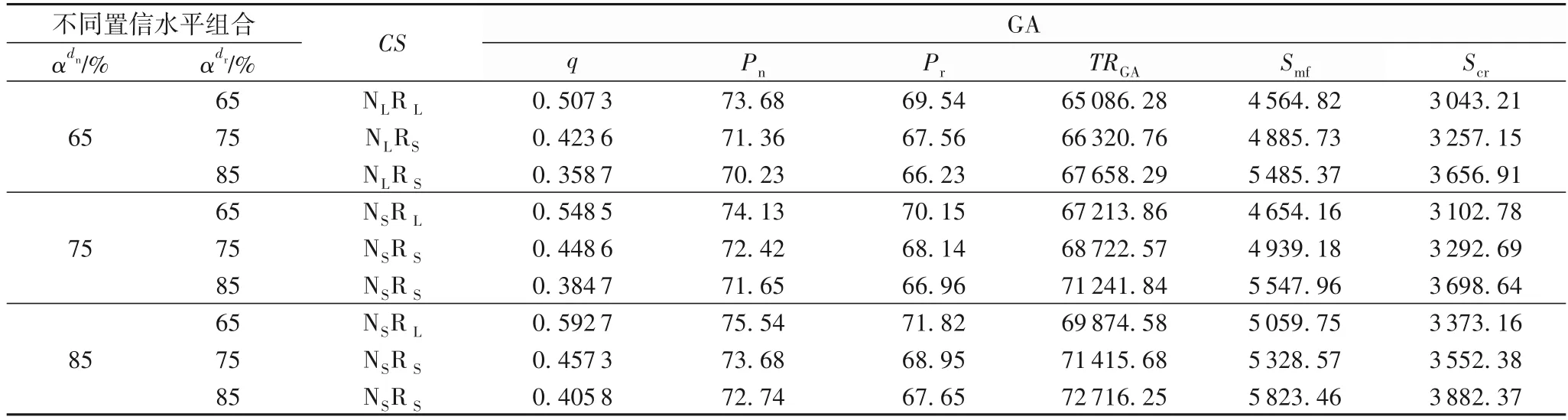
表7 采用GA求解不同置信水平下的最優決策Tab.7 Optimal decision at different confidence levels by using GA

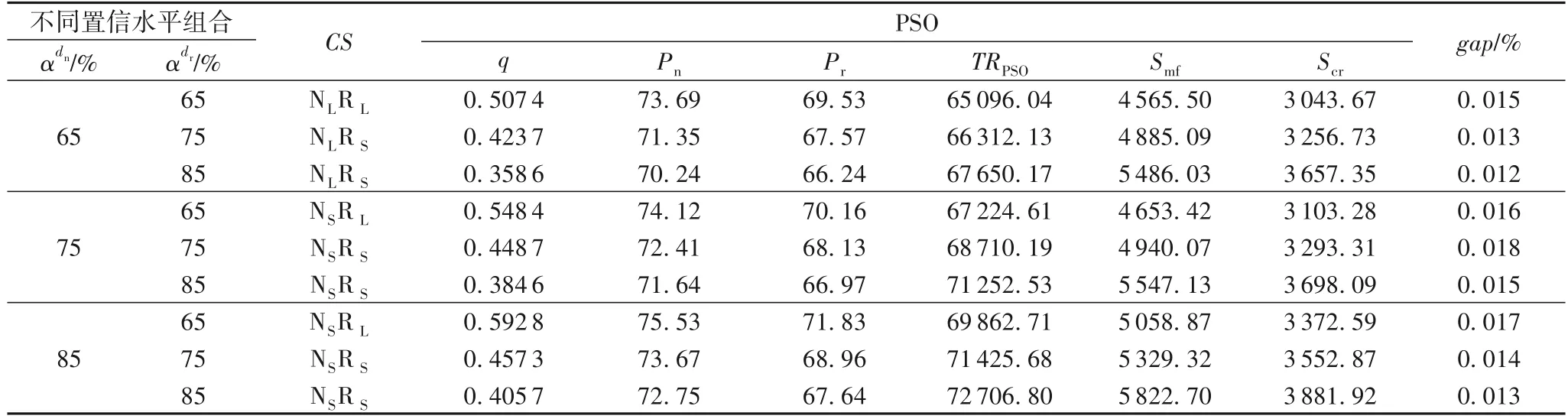
表8 采用PSO求解不同置信水平下的最優決策Tab.8 Optimal decision at different confidence levels by using PSO

管理啟示：①隨著再制造品潛在需求置信水平的增加，企業應生產較多的再制造品，通過增加政府補貼額來提高總利潤；②隨著新產品潛在需求置信水平的增加，企業應生產較多的新產品，通過降低采購運營成本來提高總利潤；③企業可以根據新產品和再制造品潛在需求置信水平的不同組合制定最優回收、生產和銷售決策，逐漸提高總利潤。

3.2 不確定環境下的最優渠道結構選擇

在新產品和再制造品需求不確定環境下，為進一步可視化分析銷售渠道結構的最優選擇問題，本文將銷售渠道結構數值量化為：第1 至第4 種渠道結構分別賦值1、2、3、4，銷售渠道數值量化為：直銷渠道賦值10，分銷渠道賦值20。

管理啟示：①不確定新產品和再制造品需求會影響最優銷售渠道結構選擇，企業可以結合不同潛在需求置信水平，對銷售渠道進行調整；②隨著新產品和再制造品潛在需求置信水平的增加，企業應將新產品和再制造品從分銷渠道逐漸調整為直銷渠道；③企業可以根據不同潛在需求置信水平組合選擇最優銷售渠道結構，逐漸提高總利潤。

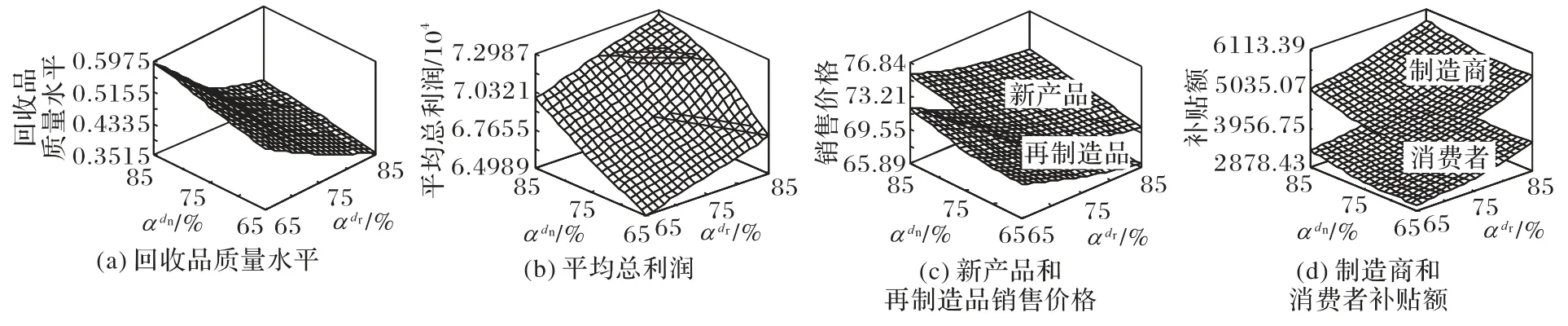
圖4 不同潛在需求置信水平對最優決策的影響Fig.4 Influence of different confidence levels of potential demands on optimal decision

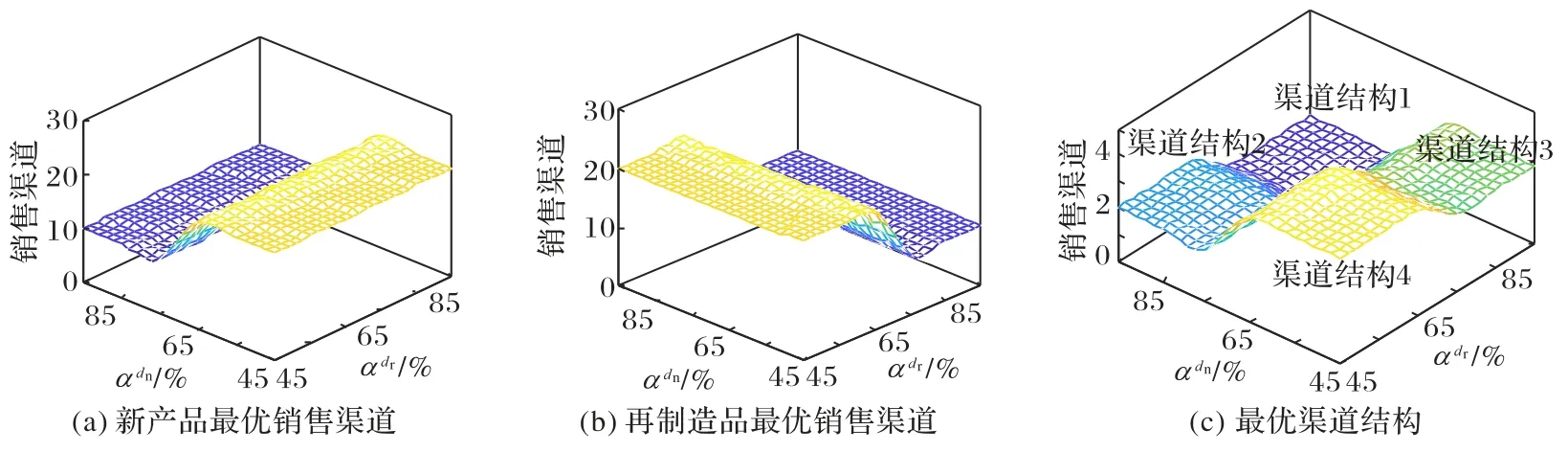
圖5 不同潛在需求置信水平下的最優銷售渠道和渠道結構Fig.5 Optimal sales channels and channel structures under different confidence levels of potential demands

4 結語

基于不確定市場需求和回收品質量水平，綜合考慮政府差別權重補貼和直銷平臺費用，構建了四種銷售渠道結構下的閉環供應鏈系統總利潤模型，研究了閉環供應鏈系統的最優決策問題。采用PSO算法和GA對比求解模型算例，驗證了算法的效度和模型的信度。

本研究可為企業在不確定環境下制定回收、生產和銷售策略提供參考，同時為企業選擇最優銷售渠道結構提供借鑒。本文采用PSO 算法和GA 求解模型，進一步研究可以考慮ACO算法、ABC算法等其他元啟發算法。