基于改進Elman神經網絡的制糖企業原糖需求預測模型

李洋瑩，陳智軍，張子豪，游 蘭

（湖北大學計算機與信息工程學院，武漢 430062）

0 引言

制糖業是多類行業的基礎工業，在我國的國民經濟中具有不可或缺的地位［1］。制糖原材料的供需平衡直接影響著企業生產效率，通過人工智能方法針對原材料供需規律建模，是實現企業高效生產的有效方法，也是制造型企業智能化轉型的重要信息化指標之一。

需求量預測是一種定量預測，較為常用的預測手段為時間序列預測法。時間序列預測法由數學家Yule 在1927 年提出，自回歸模型（Auto-Regressive Model，AR）可用來預測未來市場變化規律［2-3］，隨后自回歸移動平均模型（Auto-Regressive Moving Average Model，ARMA）和 .動 .均模型（Moving Average model，MA）的提出則揭開了國內外學者研究時間序列的序幕［4］。時間序列預測旨在通過研究對象本身所具有的數據變化規律，在時間基礎上擬合出數據的規律性，在解決線性時間序列的擬合問題上有著出色表現。但現實中多為非線性復雜問題，相較于傳統的時間序列預測方法［5-7］，引入神經網絡可以更好地解決非線性時間序列的擬合問題。武乃虎等［8］采用時間序列和神經網絡改進模型，解決了風速和風電功率之間存在的非線性關系對預測精度的影響；Wang 等［9］提出了基于長短期記憶的順序神經網絡預測模型，可用于預測給定頁面深度處的廣告將在用戶屏幕上顯示特定停留時間的概率。

目前，國內外需求量預測相關研究已積累了一些成果，但較少考慮行業特點對需求量預測的影響，準確性有待提高；同時，食品加工業中原材料采購主要以周為周期，而現有研究多以月和年為預測時間長度，導致現有方法難以滿足預測的時效性要求。針對上述問題，本文基于制糖企業原材料供需錯位與時間特征因素的關系分析，充分考慮了以周為單位的原糖采購量預測的時效性要求，在多時間粒度下提出一種時間特征關聯的使用改進布谷鳥搜索（Modified Cuckoo Search，MCS）算法優化的Elman神經網絡需求量預測模型TMCS-ENN（Temporal feature-correlated MCS-Elman Neural Network）。

本文主要工作如下：

1）提出了自適應學習速率公式優化Elman 神經網絡（Elman Neural Network，ENN）學習速率。在神經網絡迭代過程中，不斷將當前誤差與上一次誤差對比，自適應地調整學習速率逼近最優解，提升了ENN 的收斂速度，并增強了其局部搜索能力。

2）通過對歷史大量數據的特征分析，并結合制糖企業原材料購買的時間相關性與滯后性規律，將歷史數據進行基于周粒度的短時數據切片設計，并以節假日作為重要特征因子優化ENN 的模型預測，提高了模型預測精度。在多時間粒度下進行對比實驗，并在短時預測的精細時間粒度下滿足了制糖企業對于原材料購買的時效性要求。

3）提出了改進布谷鳥搜索（MCS）算法優化ENN 的權值和閾值。引入自適應的寄生失敗概率和自適應的步長控制量公式，使得算法在更新過程中充分利用鳥巢位置信息，加強局部搜索，改善了算法的收斂速度和解的質量。

4）TMCS-ENN 可以較好地為原糖需求量購買提供精準預測，而且該方法可以遷移到其他時間相關的需求預測場景進行預測，能為企業原材料需求預測提供重要的參考。

1 面向原糖預測的Elman神經網絡

1.1 研究思路

制糖原材料需求量預測的研究是一個典型的時間序列預測問題。對于制糖企業，在日常的生產活動中制糖原材料的需求量通常受到購買價格、產品銷量以及采購時間等多方條件限制，使其具有較為鮮明的非線性特點。針對非線性問題，傳統時間序列預測模型具有一定局限性，導致最終結果往往不佳［10-11］。神經網絡的出現彌補了傳統時序預測模型的不足，因此，本文選擇神經網絡作為原糖需求量預測的基礎模型。

一般的靜態神經網絡的輸出僅依賴于當前輸入，不具備記憶性，因此對解決具有時序依賴關系的時間序列預測問題，效果往往不夠理想。為使系統具有記憶性，達到適應時變的目的，Elman 神經網絡（ENN）［12-13］具有內部反饋與前饋相連的結構特點，從而具備記憶特性［14-15］。圖1 展示了ENN 的模型結構。ENN 將承接層作為隱含層中增加的一步演示算子，通過收集與存儲隱含層的輸出值，解決了神經網絡不具有動態記憶功能的問題。

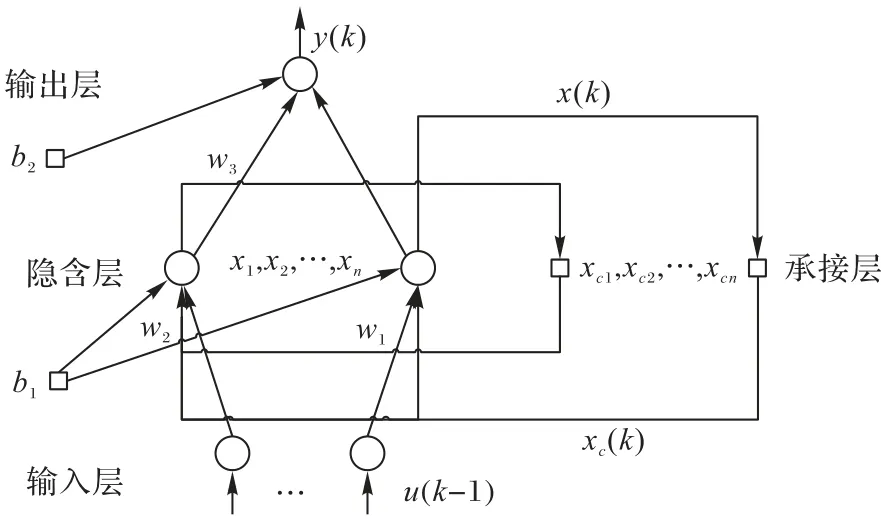
圖1 Elman神經網絡結構Fig.1 Structure of Elman neural network

人類的某些特殊活動會對整個社會以及各個行業產生一定的影響［16］，如受我國傳統習俗影響，節假日會造成制糖原材料需求量的波動，某些傳統節日如元宵節、中秋節，對糖消耗量較大，日不均勻系數會受到較大的影響。根據調研制糖企業業務流程以及對基礎數據的分析，制糖企業的采購頻率具有一定規律，一般分為周采購、半月采購、月采購。圖2展示了部分采購量變化趨勢：從圖2（a）中可以看到，1 月因春節與元宵節，原糖采購遠超其他月份；在圖2（b）展示的每半月購買數據中，也體現出了類似的趨勢；圖2（c）展示了第31 周至第44周的原糖購買量，其中，第40 周為國慶節假日，對于原糖的購買量也遠超過近鄰幾周。可見制糖原材料采購量的增長和節假日具有一定的關聯性，這些波動具有一定的規律性和相對穩定性，因此可依據其變化規律進行預測。本文采取與制糖原材料需求量預測關聯最大的節假日因素進行需求量預測。

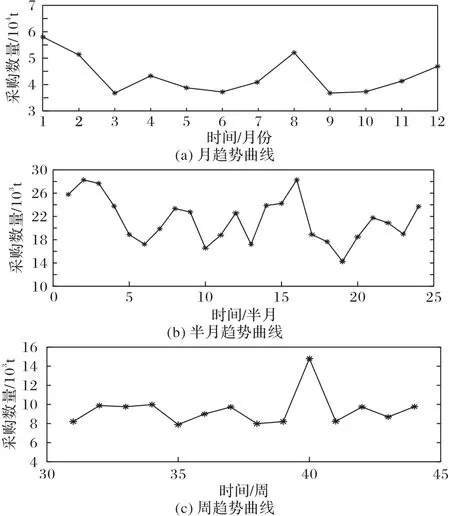
圖2 原糖采購量與采購周期的關系Fig.2 Relationship between raw sugar procurement volume and procurement cycle

1.2 自適應網絡學習速率優化ENN

數據源維度決定了ENN 輸入層的節點個數，研究對象則決定其輸出層節點個數。通過對企業原糖相關歷史數據的分析，數據源可被劃分為以下四類：原糖采購量、原糖消耗量、成品糖銷售量以及時間特征，研究對象則為原糖需求量的預測值。因此，針對原糖需求預測問題，本文中ENN 的輸入層節點數和輸出層金額點數分別為4和1。

在ENN 中，學習速率的大小會直接影響收斂速度，學習速率過大、過小或者保持恒定都會影響最終預測結果的精準性。為此，本文提出了自適應改變學習速率的方法來提高模型的收斂速度。其基本原理為：在模型的迭代過程中，將當前誤差與上一時刻誤差進行比較，若二者相對接近，則說明此時已經接近最優解，考慮增大學習速率以提高收斂速度；若二者相差較大，則表明當前解已偏離最優解，考慮減小學習速率，并結束當前操作。自適應網絡學習速率如下所示：

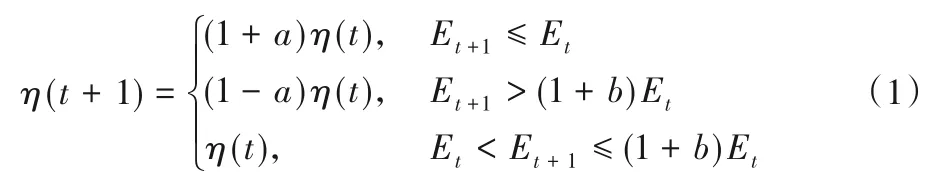
其中：η(t)和η(t+1)分別表示當前迭代過程和下一次迭代過程的模型學習速率；Et和Et+1分別表示當前誤差和迭代下一次的誤差；a、b均為正小數，對學習速率進行限制。本文中a、b取值均為0.05。

根據式（1），本文實驗中設置網絡的學習訓練次數、目標精度以及誤差精度分別為5 000、0.1和0.000 1時，TMCS-ENN效果最佳。

1.3 TMCS-ENN設計

時間序列預測實質為一種非線性的、約束繁雜并且可能存在多局部極值的最優化問題。制糖企業原材料需求量預測具有十分典型且復雜的非線性特點，原糖需求量受諸多因素影響，使用傳統算法很難在有限的時間和空間內做出準確有效的應答。布谷鳥搜索（Cuckoo Search，CS）算法作為一種新興的元啟發式算法，具有參數少、易實現、效果好等眾多優點，能夠快速、高效地解決非線性的復雜問題，該算法的研究基于布谷鳥的巢寄生行為與萊維飛行機制［17］，通過采用萊維飛行更新解，避免頻繁陷入局部最優解，使算法的全局搜索能力更強，在此過程中需對部分解進行丟棄并更新。

考慮到節假日對于原糖需求量有直接顯著的影響，本文采用了時間特征關聯的使用MCS算法優化的Elman神經網絡需求量預測模型TMCS-ENN，其流程如圖3 所示，其中的時間特征優化、神經網絡權值和閾值的初始化以及MCS 算法是TMCS-ENN預測模型的主要改進。

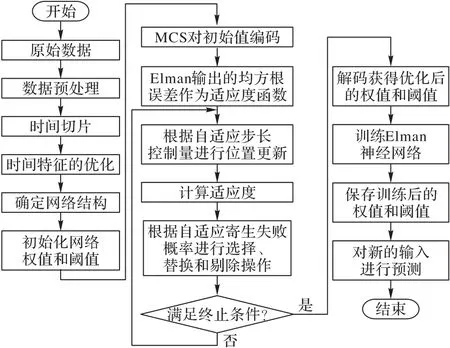
圖3 TMCS-ENN預測模型的流程Fig.3 Flowchart of TMCS-ENN prediction model

1.4 改進布谷鳥搜索（MCS）算法

CS 算法具有易實現、參數少、效果好等眾多特點，常用于解決具有非線性特點的優化問題［18］。由于CS 算法具有收斂速度慢和全局搜索仍然不徹底的現象，為改善其性能，通常需要采取一定方式對該算法進行改進。因此，本文從自適應的寄生失敗概率和自適應的步長控制量兩方面對CS 算法進行優化，得到MCS算法。

1.4.1 自適應的寄生失敗概率優化

寄生失敗的概率用Pa表示，在標準的CS 算法中Pa保持不變，但在CS算法中，無論較優鳥巢解還是較差鳥巢解，在迭代過程中均會以概率Pa出現寄生失敗現象。寄生失敗概率Pa越大，則較優鳥巢解越容易被新的鳥巢解所替換，導致算法很難收斂至最優解；Pa越小，則較差鳥巢解越可能被保留，從而使得收斂變慢。

針對上述問題，CS 算法的迭代過程中，前期應通過一個較大概率接受新解，從而提高收斂速度；在后期應使用較小的概率去保留較優解。為實現這樣的迭代效果，本文提出一種自適應的寄生失敗概率Pa，如式（2）所示：

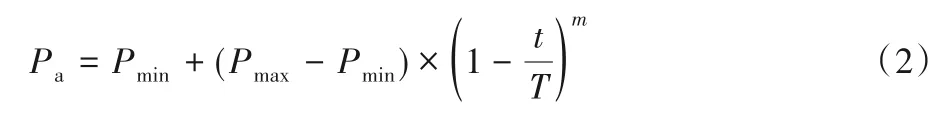
其中：Pmin和Pmax分別表示最小寄生失敗概率以及最大寄生失敗概率；t和T分別表示當前迭代次數與最大迭代次數；m是一個取值大于0 的非線性因子，其作用為控制寄生失敗概率的減小速率。分析式（2）可知，當m取值小于1，可以實現Pa在初期較大，而后期急速變小的效果。因此，本文Pmax和Pmin分別取0.5 和0.1，m和迭代次數取值分別為0.5 和500。Pa隨迭代次數的變化曲線如圖4 所示。可以看出，在迭代優化的早期過程中，寄生失敗概率維持在一個較大取值范圍內緩慢降低，而在后期則迅速變小，從而實現了寄生失敗概率Pa的自適應效果。

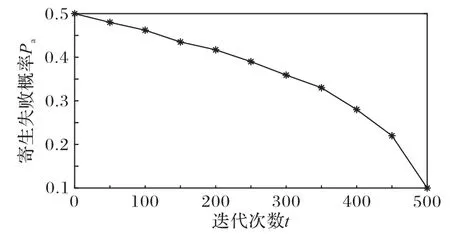
圖4 Pa隨迭代次數變化曲線Fig.4 Variation curve of Pa with iterations

1.4.2 自適應的步長控制量優化

萊維飛行的路徑是一種隨機行走，其行走步長服從重尾分布，因此CS 算法在全局空間上表現出了較強的隨機跳躍性，使其全局尋優能力較強；但由于其長步與短步分別以低頻率和高頻率交替出現，使用CS算法在全局空間中搜索鳥巢附近位置時極有可能搜索不徹底，忽略某些解。并且隨著迭代的不斷增加，長步長的出現可能會導致較優鳥巢位置被跳過，并使其附近的局部信息無法利用，使得算法很難在最優解處收斂，造成算法的收斂精度不高。

針對上述現象，本文提出一種自適應步長控制量，可有效控制CS算法的迭代步長，避免優秀位置解被跳過從而導致算算法收斂精度低的問題。

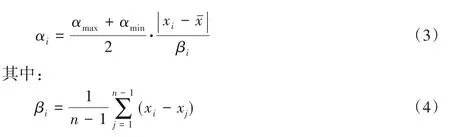
式中：xi為當前鳥巢位置解；αi為xi的下一個步長；αmax和αmin分別表示最大步長與最小步長，在本文中取值分別為1.5 和0.5；xˉ表示當前所有鳥巢位置解的平均值；βi表示當前鳥巢位置解與其他鳥巢位置解的平均差值。由式（3）可知，αi與當前鳥巢位置解和平均鳥巢位置解的差值的平均值成正比，因此可以自適應地對步長進行調整。這種自適應步長控制方法可以更好地利用局部信息，減少了原先算法由于跳躍性所導致的缺陷，提高了算法在全局空間中找到全局最優的可能性。

若對ENN 的閾值和權值進行隨機初始化，往往會使得網絡陷入局部最優，并降低收斂速度。為此，本文使用MCS 算法對模型進行優化。由于每個鳥巢都可能是ENN 的最優閾值與最優權值，使用均方根誤差作為適應度函數計算ENN 的最優權值與最優閾值。MCS 算法會不停地進行迭代運算，一直達到收斂條件（達到迭代次數或滿足最小均根方誤差），MCS 優化Elman 神經網絡（MCS-ENN）的流程如圖5 所示。ENN 相關參數在1.2 節已給出，MCS 算法的自適應寄生失敗概率和自適應步長控制量分別初始化為0.5和1.5，根據實驗數據量將鳥巢數n、迭代次數T和精度e分別設置為75、500和0.000 1。

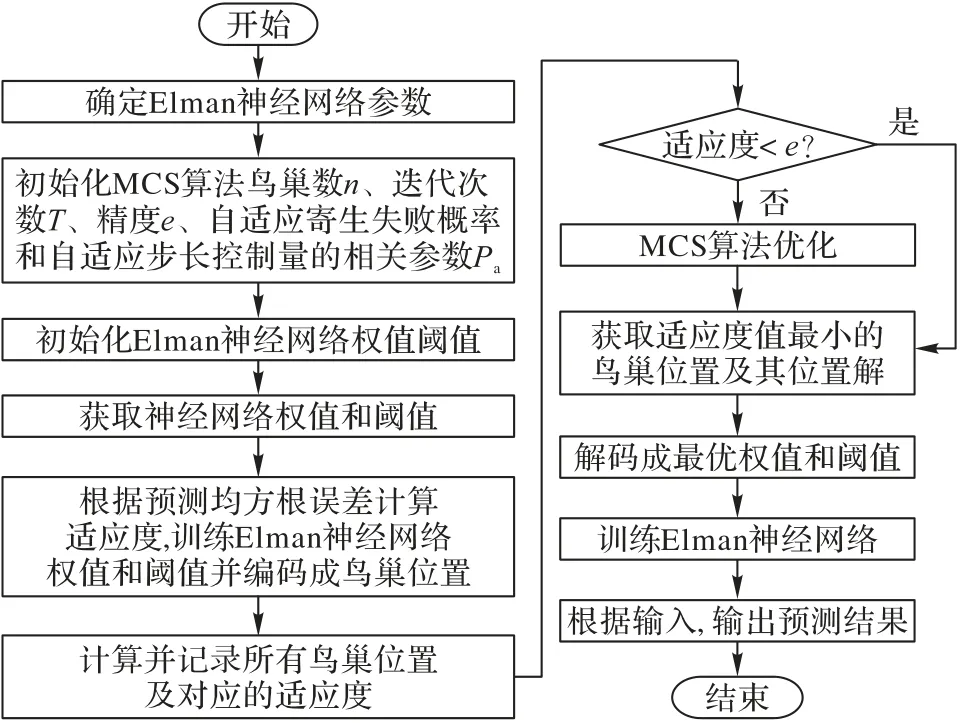
圖5 MCS-ENN流程Fig.5 Flowchart of MCS-ENN

1.5 利用時間特征優化ENN

中國節假日因其特有的文化傳統對于人的行為具有一定的導向作用，例如，中秋節時月餅的銷量會達到一年中的峰值。由于各個節假日活動對食品有不同的要求，而糖作為基礎食品材料，需求量受到節假日因素影響在一定范圍內有規律地波動。可見，制糖原材料的需求量與時間序列存在相互依賴關系，若預測時仍按照平時生活方式進行預測，將會與真實值產生較大誤差，降低預測精度。本文針對節假日原材料需求量變化的特點，對模型進行改進。

針對制糖原材料的時間高度敏感性，本文首先對數據分別按照“月”“半月”和“周”的時間粒度對數據進行切片，同時，以“0”“1”標簽的形式標識每條數據中是否包含節假日因素，如春節、元宵節等，“1”表示劃分的時間片內包含節假日因素，“0”則相反。將改進數據的節假日特征作為預測模型的影響因子，作為輸入變量對模型進行優化。

在MCS 算法優化的ENN 中加入節假日時間特征后，預測模型更加符合制糖企業的真實情況。通過對時間特征進行分析，提取節假日因素，加入節假日因素的TMCS-ENN的具體算法如算法1所示。

算法1 加入節假日因素的TMCS-ENN。

2 實驗設計與分析

2.1 原始數據

本文研究的制糖原材料數據來源于某真實制糖企業，實驗選取了制糖企業近5年共60個月的歷史數據。本次實驗數據集的主要結構描述如表1～3。

表2 原材料消耗數據集描述Tab.2 Description of raw material consumption data set

表3 成品糖銷售數據集描述Tab.3 Description of sugar sales data set

2.2 數據預處理

對于原材料需求量預測模型，首先需要對模型的輸入輸出、訓練樣本進行確定，也就是樣本數據的確定。真實而完整的數據有助于提高預測原材料需求量的精準度，然而用于預測原材料需求量的數據大多來源于單機系統、地磅稱重數據以及相關單據，因此需要對數據進行預處理，這是原材料需求量預測必不可少的環節［19］。

2.2.1 數據清洗與時間切片

制糖原材料數據因其來源可能出現數據異常、空缺、不一致等問題，會嚴重影響數據分析的準確性，所以需要通過對原數據進行清洗從而得到更加精準的預測結果。原始數據中的字段不能完全應用于預測模型，為降低計算量，本文對數據進行預處理時剔除了與預測無關的屬性。

空值數據可能會對模型預測結果產生一定的影響，因此，對該類數據進行處理十分必要。在進行預測時，若空值數據不影響預測結果，就不予考慮；若空值數據是關鍵數據，則不能忽略。本文針對這樣的關鍵性數據會根據時間選取該數據前后半個月的數據求平均值，以對該空缺數據進行填充。

由于數據本身的復雜性，不能直接體現其具有的時間特征因素。本文選擇以周、半月、月的時間粒度分別對現有數據進行時間切片，以周粒度為例，一條數據包括一周內的原材料購買量與實際消耗量等，切片后的數據從第1周開始生成對應ID。此外，每條數據以“0”表示不具有節假日，“1”表示具有節假日，作為數據的時間特征以及預測模型的影響因子之一參與模型優化，經過數據清洗與時間切片后的樣例如表4所示。

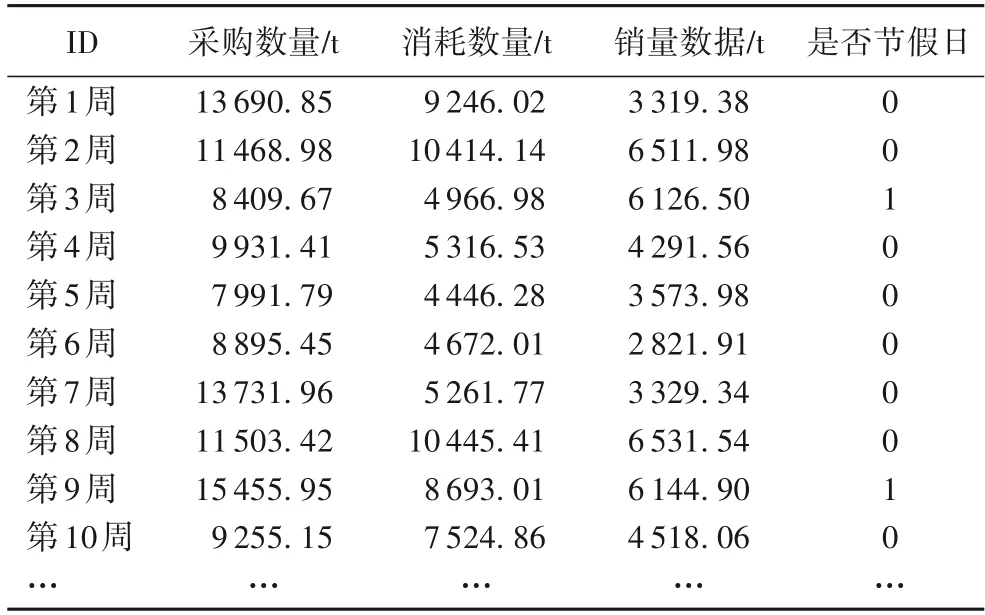
表4 巴西原糖數據時間切片樣例Tab.4 Worked-example of Brazil raw sugar data after time slicing

2.2.2 數據轉換與數據歸并

針對制糖原材料預測，若直接使用原始數據作為預測模型的訓練樣本，預測結果的誤差往往偏大，也會產生飽和的現象。因此對于歷史數據，首先要對輸入變量進行歸一化處理，避免沒有經過處理的數據影響到預測效果。本文將制糖企業原材料的數據樣本使用2.2.1 節中歸一化方式處理至［0，1］范圍。

數據歸并是在已有的數據特征中，根據任務目標需求尋找有用的特征，在不失真的條件下盡量精簡數據。對于原材料采購數據，相同對象因為所處環節不同可能會出現屬性值各不相同的現象，需要通過歸并解決數據冗余和不一致的問題。

2.3 預測模型評價指標

為了驗證模型的效果和性能，本文采取均方根誤差（Root Mean Squared Error，RMSE）、平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）以及預測精度（Forecasting Precision，FP）這三種指標進行評價。具體指標計算公式如下：

2.4 結果分析

本節實驗共分四組：首先驗證CS 算法對于ENN 的優化（記作CS-ENN）；其次，通過MCS 算法和CS 算法的對比實驗，驗證MCS 算法是否較CS 算法有更好的優化效果；接著，驗證加速時間特征因素后的TMCS 算法的優越性；最后，在不同時間粒度下對比TMCS-ENN和MCS-ENN的預測效果。

本文實驗選取的原材料預測樣本為某制糖企業2013年1月到2017 年12 月近5 年的巴西原糖采購的歷史數據。為保證預測的準確性和可比性，四組實驗都采用巴西原糖作為原材料預測未來10 個時間節點的情況。對周時間粒度實驗，共有165 周巴西原糖數據，其中前155 周數據作為訓練樣本，最后10 周（2017 年前10 周）數據作為測試樣本，對網絡進行訓練和預測；TMCS-ENN加入了節假日因素，輸入層個數設為4。對于按月預測，選取數據量共120 個月數據，其中前110 個月作為訓練樣本，后10 個月為預測樣本；對半月預測，選取數據量共120 個半月數據，其中前110 個半月作為訓練樣本，后10個半月為預測樣本。

2.4.1 權值優化對預測模型的影響

本組實驗比較CS算法優化權值、閾值的ENN與采取隨機權值閾值的ENN 模型預測精度。在周時間粒度下進行實驗，預測結果和百分比誤差如圖6 所示。由實驗可得，CS-ENN 的均方根誤差（RMSE）為0.102，平均絕對百分比誤差（MAPE）為8.72%，預測精度為91.28%；ENN 的三項指標則分別為0.173、12.15%以及87.85%。由圖6 可知，巴西原糖需求量在第6 周（春節）和第8 周（元宵節）明顯增高，并且CS-ENN 模型預測結果更好，其預測精度比ENN 高3.43 個百分點，誤差明顯減小，可見，由CS 算法優化的ENN 在一定程度上能夠提高預測精度。

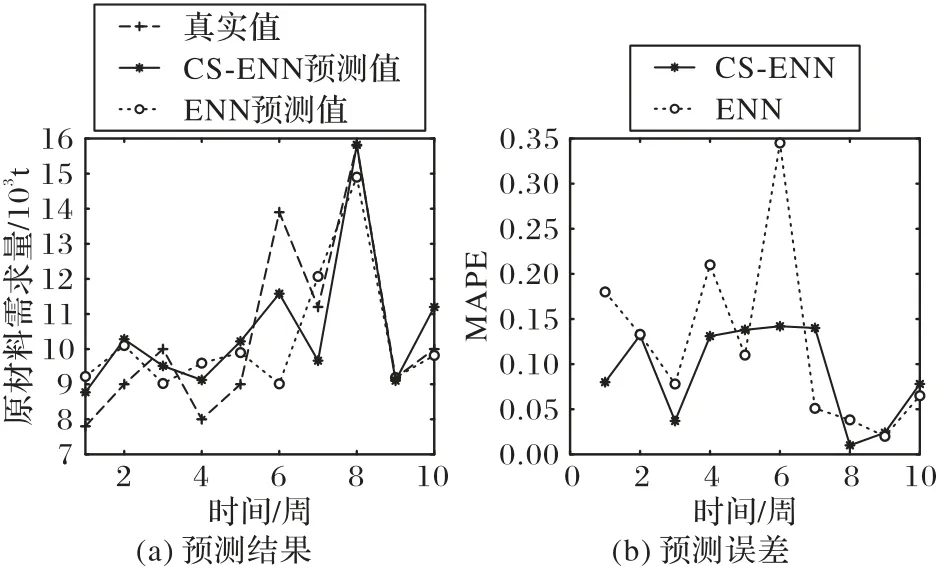
圖6 CS-ENN和ENN的預測結果及誤差比較Fig.6 Comparison of CS-ENN and ENN in prediction results and errors

2.4.2 MCS算法對預測模型的影響

本組實驗比較在MCS 算法優化下使用自適應寄生失敗概率和自適應步長控制量的ENN 預測模型與CS-ENN 預測模型的預測精度。在周時間粒度下進行實驗，預測結果和百分比誤差如圖7 所示。實驗結果表明，MCS-ENN 的均方根誤差（RMSE）為0.067，平均絕對百分比誤差（MAPE）為6.11%，預測精度為93.89%；而CS-ENN 對應各項指標分別為0.096、9.38%和90.62%。MCS-ENN 的預測精度較CS-ENN 提高了3.27 個百分點，誤差明顯減小，說明MCS 算法對于模型的優化效果更為明顯，能夠提高預測模型的精準度。

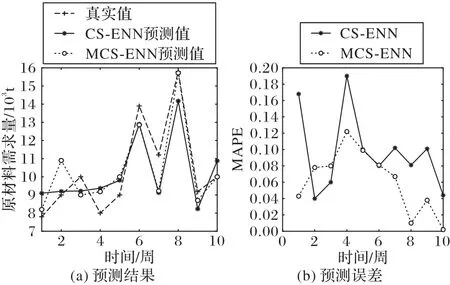
圖7 MCS-ENN和CS-ENN的預測結果及誤差比較Fig.7 Comparison of MCS-ENN and CS-ENN in prediction results and errors

2.4.3 時間特征對預測模型的影響

本組實驗比較加入節假日時間特征后對MCS-ENN 的影響。以周為時間粒度進行實驗，預測結果和百分比誤差如圖8 所示。實驗結果表明，加入節假日特征的TMCS-ENN 的均方根誤差（RMSE）為0.058，平均絕對百分比誤差（MAPE）為5.36%，預測精度為94.64%；而未考慮該特征的MCS-ENN 的對應各項指標分別為0.092、6.73%和93.27%。加入時間特征可以使得預測模型精度提高1.37 個百分點。圖8 中第6 周（春節）需求量明顯提高，這是因為該節點具有節假日的時間特征，而在加入節假日因素后預測誤差明顯變小，再次說明加入時間特征對預測模型有優化作用，能夠提高預測模型的預測精度。

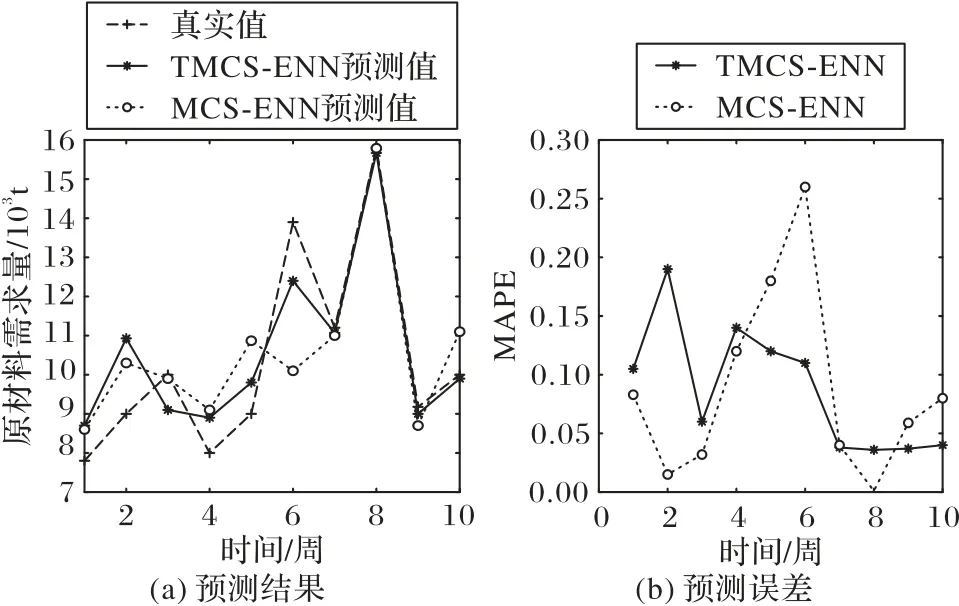
圖8 TMCS-ENN和MCS-ENN的預測結果及誤差比較Fig.8 Comparison of TMCS-ENN and MCS-ENN in prediction results and errors

2.4.4 時間粒度對預測模型的影響

為進一步探究不同時間粒度下，TMCS-ENN 預測模型的表現情況，本組實驗將時間粒度劃分為月、半月以及周分別進行實驗。其中，MCS-ENN 輸入層個數為3，隱含層個數為5。實驗得到預測結果和百分比誤差如圖9所示。

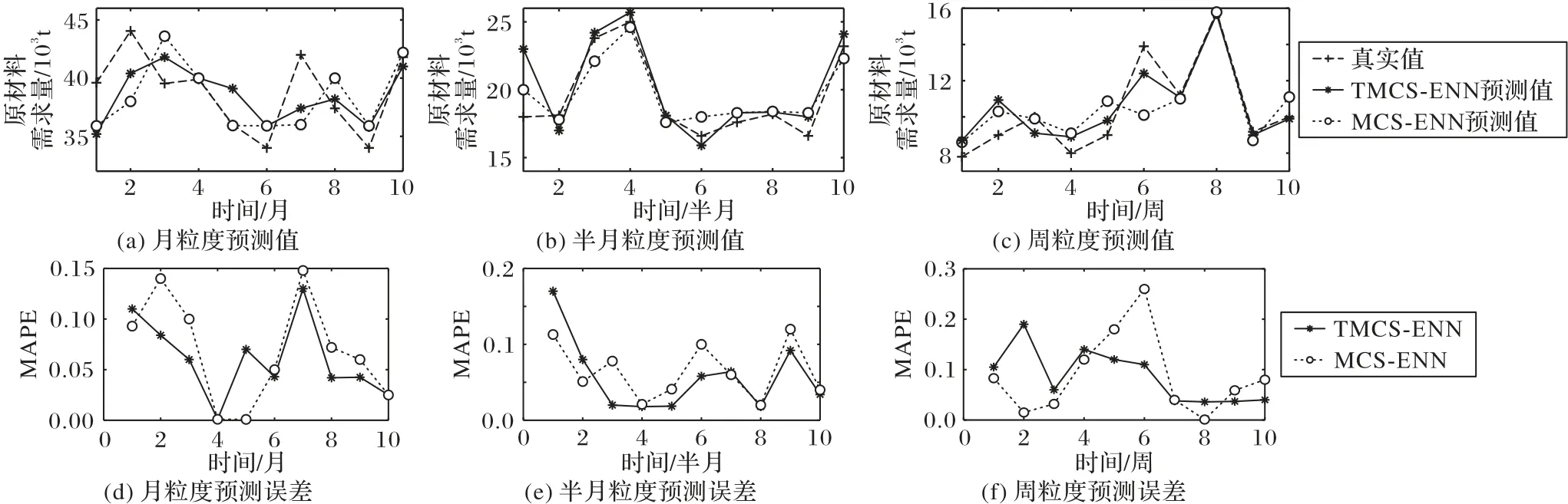
圖9 不同時間粒度TMCS-ENN和MCS-ENN的預測結果及誤差比較Fig.9 Comparison of TMCS-ENN and MCS-ENN in prediction results and errors under different time granularity

為進一步驗證實驗可信度，本文共對5 年歷史數據匯總的數據進行了5 次預測，并對最終結果取均值后得到對比結果如表5所示。表5較為直觀地展現出了在不同時間粒度下，TMCS-ENN 預測模型與MCS-ENN 預測模型各項評價指標的對比。由表5 可以看出，通過加入時間特征，模型預測精度相較未加入時間特征的MCS-ENN 模型的預測精度在月粒度下提高了1.02 個百分點；在半月粒度下提高了0.82 個百分點；在周粒度下提高了1.44 個百分點。對于同一模型，時間粒度劃分越細，則預測精度及其余各項評價指標越好。實驗數據表明，加入時間特征可進一步提高模型預測精度，有利于指導企業生產。

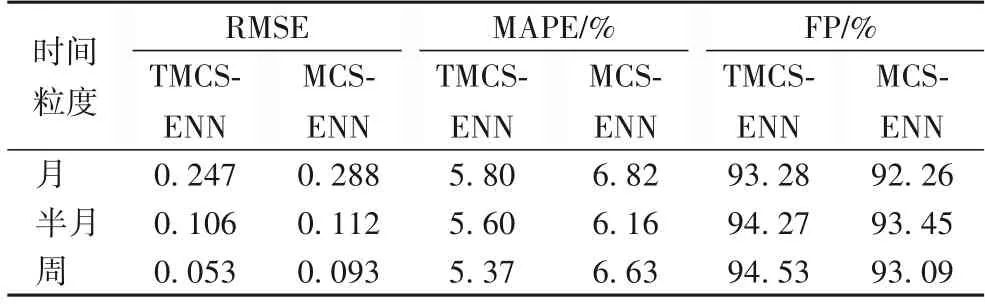
表5 不同時間粒度下的TMCS-ENN和MCS-ENN的評價指標對比Tab.5 Comparison of evaluation metrics of TMCS-ENN and MCS-ENN under different time granularity

通過以上四組實驗對比，從預測精度及誤差可以看出，CS-ENN 在任何情況下的預測精度均高于ENN；MCS-ENN 的預測精度相較于CS-ENN 預測的精度有進一步提高，表明本文對于CS算法的改進可以提高原材料需求量的預測精度；在進一步考慮到時間特征后，TMCS-ENN 預測模型的預測精度明顯提高，且時間粒度越細致精度越高。可以看出，利用本文提出的TMCS-ENN預測模型將有助于制糖企業科學合理地進行制糖原材料購買。

3 結語

原糖需求的精準預測有利于提高制糖企業的生產效率。現有原材料預測研究大多采用傳統回歸、線性規劃等算法模型，忽略了時間因素影響及行業特點，預測準確性有限；同時，傳統方法難以滿足原糖需求預測的時效性要求。針對這些問題，本文提出了一種基于改進Elman 神經網絡的制糖原材料需求量預測模型。通過提出自適應學習速率公式以及MCS算法優化ENN，有效提高了模型的局部搜索能力，避免了局部最優，并結合企業與現實背景，進行基于周粒度的短時數據切片設計，使用節假日特征因子進一步提高模型預測精度。通過多組多粒度時間片段數據實驗，在周時間粒度下的短期需求預測結果較準確，符合短時預測的時效性要求。

TMCS-ENN 預測模型為原材料供需匹配一致性提供了科學可行的解決方案，為企業智能化管理提供了技術支撐；然而，并未考慮到影響需求量的其他因素，如價格稅、國內生產總值、溫濕度及天氣等，將在后續研究中進一步完善。