航空發動機中央傳動錐齒輪聲學信號分析

劉元是，文 璧，杜 軍，徐勇強，劉利源

(中國航發四川燃氣渦輪研究院，四川綿陽 621000)

1 引言

航空發動機中央傳動錐齒輪是匹配發動機和附件機構的重要部件，其主要作用是將發動機主軸轉速與功率傳遞給附件裝置。由于航空發動機的工作轉速高、轉速波動性強，極大地增加了傳動系統的動載荷。此外，因工況的變化以及負載引起的外部激勵等因素影響，發動機中央傳動錐齒輪的壽命和強度會受到極大的考驗。

齒輪裝置在運轉狀態下，若伴隨著其內部故障的發生與發展，必然會導致振動加劇以及能量增大等現象。工程中，一般通過采集齒輪振動信號對齒輪裝置進行狀態監測和故障診斷。對于航空發動機中央傳動錐齒輪而言，其高轉速的特點使得嚙合頻率最高可達10 kHz以上，因此在測試中需要很大的測試帶寬。振動傳感器測試帶寬由于安裝支座的原因受限，此外發動機復雜的測試環境也給振動傳感器的安裝帶來了相當大的困難。因此，采用振動信號對發動機中央傳動錐齒輪進行狀態監測、故障診斷存在很大的難度。

相對于振動信號，聲壓信號也是機械設備狀態的重要信息，是振動的另一種表現形式。當設備狀態發生改變時，其聲學特性也會發生改變。聲學測試由于其非接觸、高頻響和高靈敏性等優點，可在航空發動機中央傳動錐齒輪上得到很好的應用。目前國內采用聲導管系統對航空發動機中央傳動錐齒輪進行聲學測試的研究比較少，主要有力寧[1]和欒孝馳[2]等通過聲導管對航空發動機中央傳動錐齒輪開展了行波共振方面的研究。

本文在中央傳動錐齒輪專項試驗中，以聲導管系統為中間媒介，利用聲壓傳感器對其內部噪聲信號進行了采集，再通過階次、希爾伯特包絡解調、倒頻譜等方法對信號進行了分析處理，證明了聲學測試對航空發動機內部齒輪等高轉速部件的狀態進行監測、故障診斷的可行性。

2 試驗概況

試驗在中央傳動裝置試驗器上進行，圖1 為中央傳動裝置試驗器原理圖。試驗時，通過軸向力、徑向力加載器模擬主軸承在發動機實際工作中的受力，通過模擬加載或真實附件加載模擬發動機實際工作中中央傳動裝置的功率傳輸。試驗的中央傳動錐齒輪從動輪齒數為51齒，主動輪齒數為38齒。

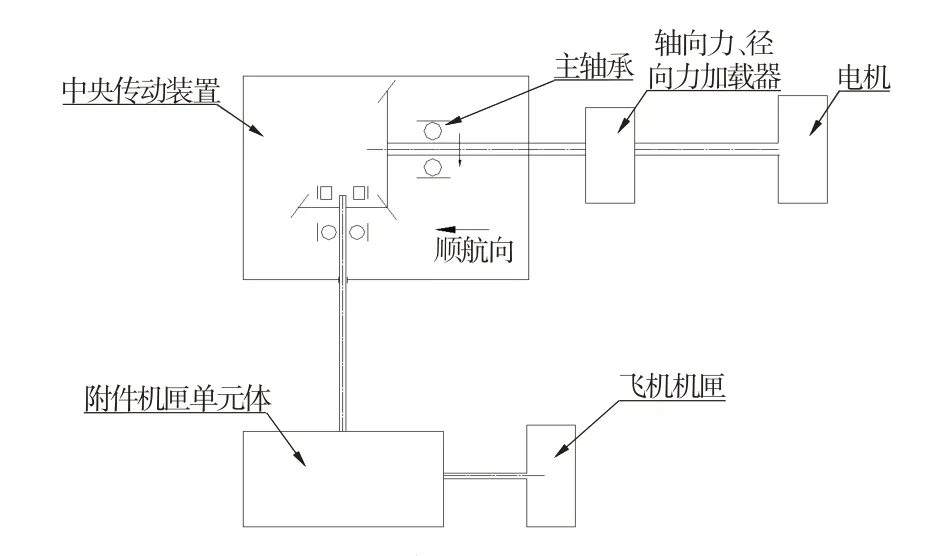
圖1 中央傳動裝置試驗器原理圖Fig.1 Schematic diagram of central gearing device

試驗測試系統框圖如圖2所示。聲壓傳感器采用自由場傳聲器，通過BNC 頭與采集系統連接，采樣率為100 kHz。試驗中，聲壓傳感器連接在聲導管上，采集齒輪箱內部噪聲；聲導管尾部與半無限長銅管相連。聲導管結構如圖3所示。

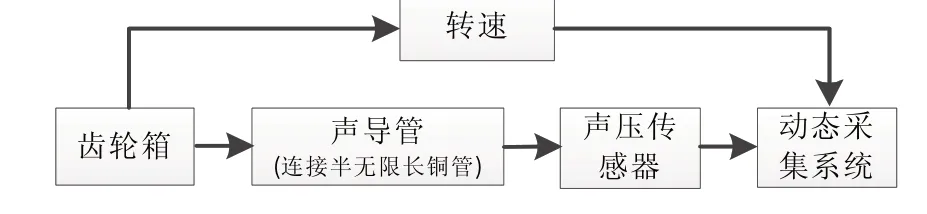
圖2 測試系統框圖Fig.2 Block diagram of test system

圖3 聲導管結構圖Fig.3 Structure diagram of acoustic duct

3 齒輪聲學信號分析

試驗過程中，齒輪箱經過掃頻增速轉速達到最大狀態后快速降至0，通過附件加載模擬發動機實際工作中中央傳動裝置的功率傳輸。試驗中通過采集系統對全程聲學信號進行采集，再利用頻譜分析法對其進行研究[3]。齒輪聲學信號頻譜一般包含齒輪轉頻及其低階倍頻、齒輪嚙合頻率及其倍頻、嚙合頻率的邊頻帶和齒輪幅的各階固有頻率等[4]。其中，嚙合頻率邊頻帶的識別對齒輪運行狀態的辨識十分關鍵。

3.1 階次跟蹤與階次分析

在采集齒輪箱內聲學信號的同時，也同步采集了旋轉軸的轉速信號，由此可以得到時間域與角度域的對應關系。此時，信號由時間域的函數轉變為角度域的函數，根據轉速的變化，通過重采樣獲得等角度采樣數據。再對等角度數據進行快速傅里葉變換(FFT)，得到幅值隨階次變化的函數，將信號由角度域轉換為階次域。圖4、圖5分別給出了試驗齒輪箱掃頻信號階次跟蹤及階次分析的瀑布圖。圖4橫軸為從動輪轉頻階次，縱軸為從動輪轉速。圖5 橫軸為信號頻率，縱軸為從動輪轉速。由圖4可知，齒輪運轉過程中，出現的頻率階次成分主要為高階轉頻，其中從動輪38階轉頻最為突出。根據從動輪齒數為51、主動輪齒數為38 可知，38 階轉頻正是該齒輪對的嚙合頻率，76 階轉頻為齒輪對的2 倍嚙合頻率。從圖5 可看出，嚙合頻率的幅值出現了數次突變，這是由于嚙合頻率隨著轉速升高而升高，在與齒輪箱內部各部件固有頻率重合時產生共振所致。此外，嚙合頻率在從動輪轉速11 000～18 000 r/min 區間內有大量邊頻帶出現。理想狀態下齒輪嚙合頻率周圍不存在邊頻帶，但實際工程中由于加工誤差以及安裝誤差影響，會導致少量微小的邊頻帶出現，若某一時刻大量邊頻帶突然出現往往伴隨著齒輪故障的發生。因此，需要對上述區間內出現的邊頻帶成分進行解調以進行后續分析[5]。

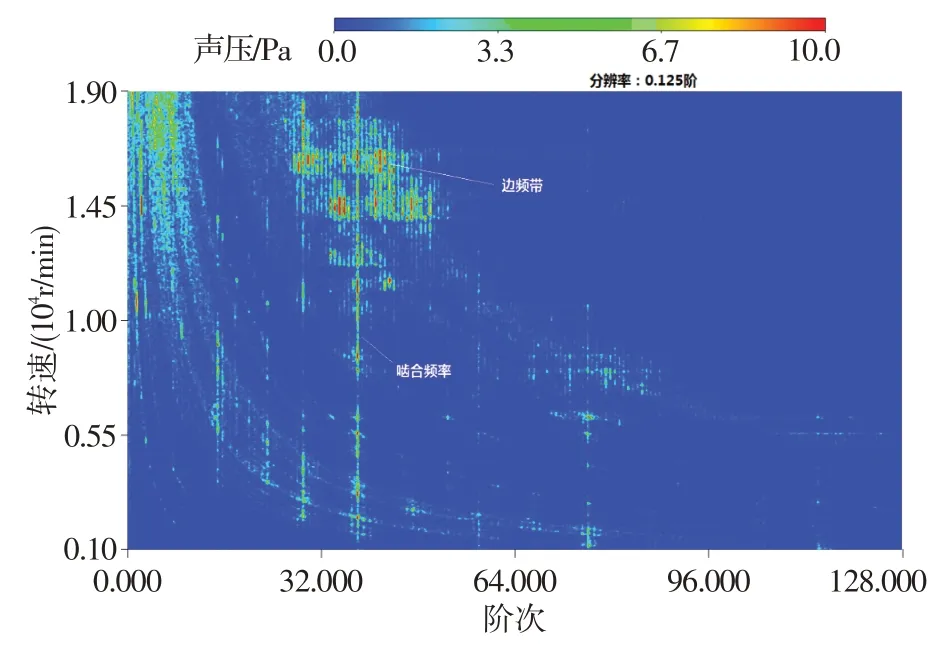
圖4 中心錐齒輪信號階次跟蹤瀑布圖Fig.4 The order tracking of center bevel gear signal waterfall diagram

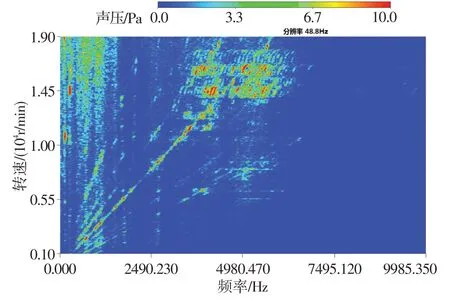
圖5 中心錐齒輪信號階次分析瀑布圖Fig.5 The order analysis of center bevel gear signal waterfall diagram

3.2 希爾伯特變換包絡解調

希爾伯特包絡是時域信號絕對值的包絡，其從信號中提取調制信號，分析調制函數的變化，對提取故障特征具有很大的優越性[6-7]。若一連續時間信號x(t)，其希爾伯特變換為：

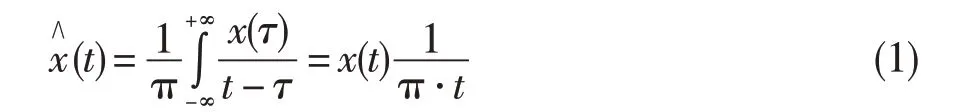
式中：t為時間變量，τ為卷積的積分變量。

(t)可以看成是x(t)通過一濾波器的輸出，該濾波器的h(t)為單位沖擊響應，其表達式為：

由信號x(t)及其希爾伯特變換(t)可構建出信號x(t)的解析信號z(t)：

信號x(t)的希爾伯特變換包絡解調為解析信號z(t)的幅值A(t)：

選取從動輪轉速為11 300 r/min與15 000 r/min時刻的信號進行包絡解調，嚙合頻率為中心頻率，帶寬為2 000.0 Hz。對信號進行希爾伯特變換后再進行FFT變換，結果如圖6所示。由圖可知，從動輪轉速為11 300 r/min 時，軸回轉頻率為188.3 Hz，此時主動輪轉速為8 420 r/min，軸回轉頻率為140.3 Hz；圖中出現的頻率主要為139.6，280.3，419.9，700.2 Hz等，與主動輪軸的轉頻140.3 Hz及其2倍頻、3倍頻、5倍頻接近。從動輪轉速為15 000 r/min時，軸回轉頻率為250.0 Hz，此時主動輪轉速為11 176 r/min，軸回轉頻率為186.3 Hz；圖中出現的頻率主要為186.5，372.1，558.6 Hz，與主動輪軸的轉頻186.3 Hz及其2 倍頻、3 倍頻接近。以上表明，該齒輪出現了齒輪嚙合頻率為載波頻率、調制頻率為主動輪軸的轉頻的情況。

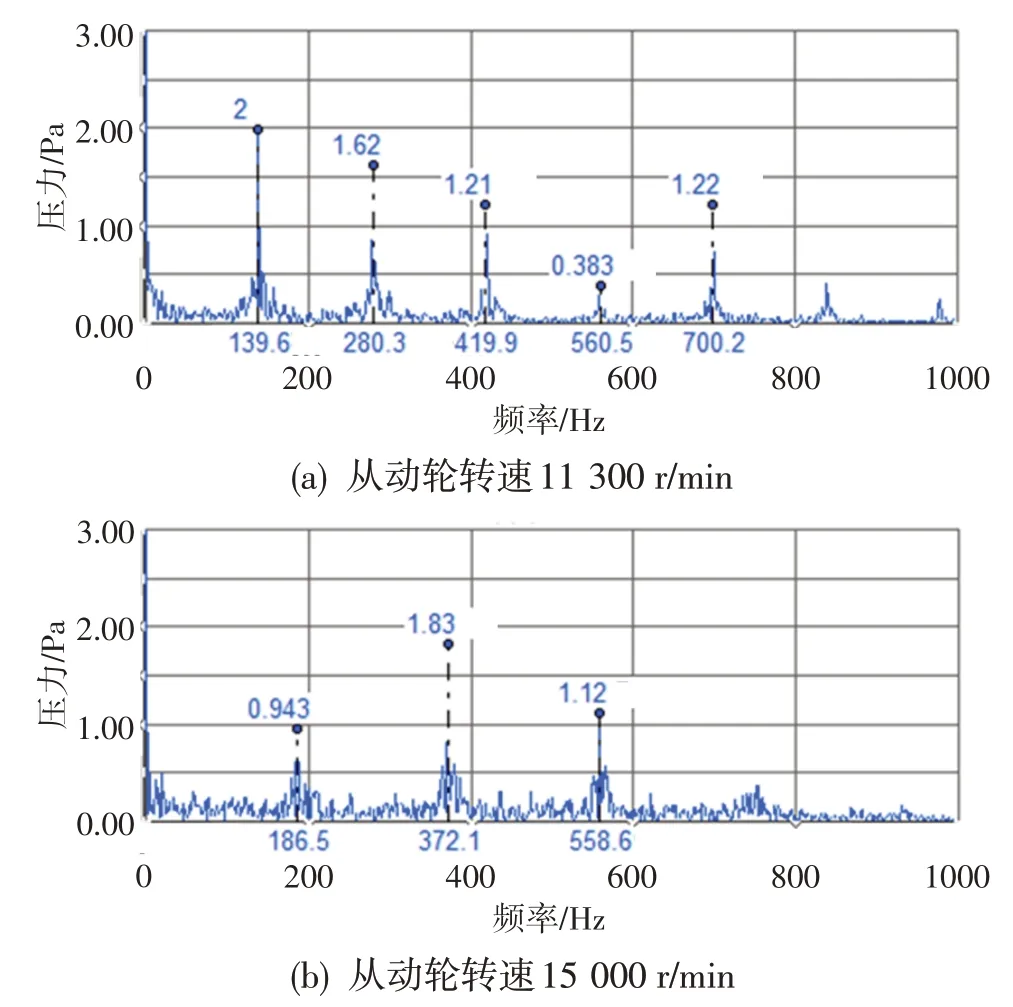
圖6 中央傳動錐齒輪信號邊頻帶包絡解調分析結果Fig.6 Envelope demodulation analysis of edge band of center bevel gear signal

故障齒輪的聲學信號通常表現為回轉頻率對嚙合頻率及其倍頻的調制，在頻譜上形成以嚙合頻率為中心的邊頻帶群。邊頻帶是故障源信息的體現，故障源的頻率由邊頻帶之間的間隔所體現，故障的程度則由幅值的變化大小所體現[3]。據此，通過希爾伯特包絡解調獲得的包含了主動輪的轉頻以及倍頻的多成分邊頻帶，初步分析認為主動齒輪可能出現了故障，下面利用倒頻譜分析對其做進一步研究。

3.3 倒頻譜分析

倒頻譜分析能夠分離和提取原信號和傳輸系統特性，是一種十分有效的齒輪故障分析方法。在齒輪信號檢測過程中，倒頻譜由于其特有性質，可從復雜的邊頻中識別出主要的信息功率譜。同時倒頻譜還能將邊頻譜中的周期成分明顯區分開[8]。幅值倒頻譜即實倒頻譜，其定義為[9]：

式中：τ為倒頻譜的時間變量，稱為倒頻率；F{}表示對括弧內的函數進行傅里葉變換；Gxx(f)表示對括弧內的函數進行子功率譜密度變換。變換過程中，倒頻譜是對數譜圖上周期性頻率成分能量的又一次集中，可以在倒頻譜圖中突出小周期信號，進而在倒頻譜中全面反映邊頻情況。在倒頻譜中能夠將邊帶間隔相等的邊頻族集中到某一倒頻分量上，據此選用倒頻譜對上述分析中出現的嚙合頻率附近的邊頻族進行分析。

同樣選取從動輪轉速為11 300 r/min 與15 000 r/min 時刻信號進行倒頻譜分析，結果見圖7。可看出，齒輪的倒頻譜出現了幾個明顯的沖擊成分。根據f=1/τ計算，從動輪轉速11 300 r/min 時沖擊點處頻率分別為140.1，70.5 Hz，分別與主動輪軸的轉頻140.3 Hz 及其1/2 倍頻接近；從動輪轉速15 000 r/min 時沖擊點處頻率分別為188.7，94.3，62.9，47.2，31.4 Hz，分別與主動輪軸的轉頻186.3 Hz及其1/2倍頻、1/3 倍頻、1/4 倍頻和1/6 倍頻接近。由此可知主動輪是故障齒輪，這與希爾伯特包絡解調分析結果相同，進一步驗證了故障發生的部位。此外，倒頻譜上出現的沖擊點主要為主動輪的1階轉頻及其分數諧頻，且從動輪轉速15 000 r/min時的分數諧頻數量相比從動輪轉速11 300 r/min時的增多，而分數諧頻一般是在齒輪磨損加劇后產生[10]，據此判斷主動輪出現了均勻磨損加劇的情況。拆卸分解發現，中央傳動錐齒輪試驗件的主動輪有均勻的輕微磨損。經分析，這是由于中央傳動錐齒輪載荷隨轉速升高而增大，在大載荷下主動輪均勻磨損加劇造成的。

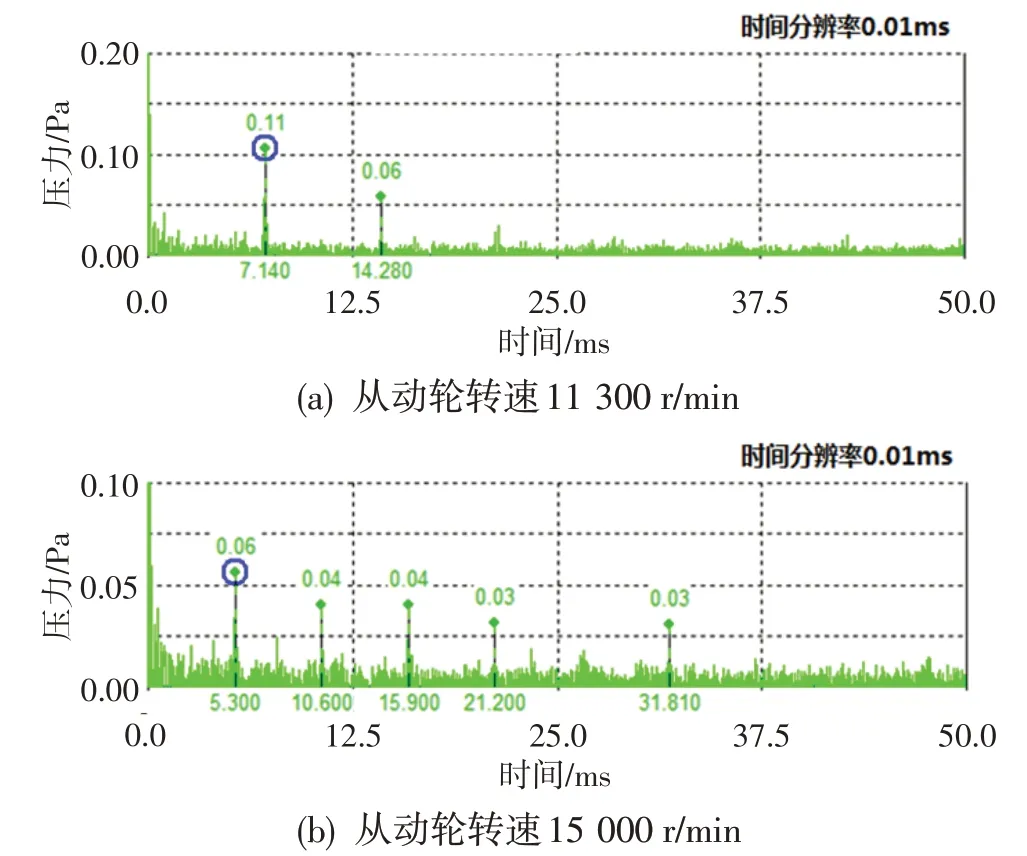
圖7 中央傳動錐齒輪信號倒頻譜分析結果Fig.7 Cepstrum analysis of center bevel gear signal

4 結論

(1) 使用聲導管系統作為媒介采集聲學信號的方法，具有非接觸、高頻響、高靈敏度等優點。該方法目前已經應用到了航空發動機傳動部件的故障辨識，以及燃燒不穩定性的研究中，有望在航空發動機測試中進一步擴大應用。

(2) 希爾伯特包絡解調和倒頻譜的分析方法對齒輪信號中邊頻帶的識別效果良好，可對齒輪的運行狀態進行有效辨識。

(3) 需要進一步解決的問題有：優化測試布局，降低測試背景噪聲；改進算法，降低算法運算時間；與其他測試方法相融合，提高診斷準確性。