LFMCW雷達高精度測距相位差改進算法*

劉 上， 朱國富， 王 玲， 陸 軍

(1. 湖南大學電氣與信息工程學院， 湖南長沙 410082； 2. 湖南大學信息科學與工程學院， 湖南長沙 410082；3. 湖南太康電子信息技術有限公司， 湖南長沙 410012)

0 引言

近年來，隨著中國基礎設施建設的振興與發展，大型工程不斷推進，雷達高精度測距技術在建筑物形變監測、湖泊液位測量、自動化汽車、目標高精度定位等方面被廣泛應用。線性調頻連續波雷達因具有結構簡單、測距分辨率高、抗噪聲能力強等特點被逐漸應用在高精度測距領域中。

線性調頻連續波雷達對單個靜止目標高精度測距的關鍵技術是準確得到回波信號與發射信號混頻后差拍信號的頻率，從而獲得高精度的測距信息。現有的高精度頻率測量方法主要有以下幾大類：比值法、基于FFT的頻譜細化算法、相位差法。典型的比值法有Rife算法[1]、Quinn算法[2-4]、Grandk算法等，這些算法利用頻譜峰值附近多條譜線的幅度比值對頻率進行校正，但接近量化頻率點時誤差較大，文獻[5-7]都針對這個問題進行了改進,但運算量大幅增加,且精度提高有限。基于FFT的頻譜細化算法首先使用少量點數FFT算法作粗估計，然后再用細化算法對頻譜的局部進行放大作細估計，主要方法有補零FFT、CZT、Zoom-FFT[8]，FFT+FT連續細化法[9-10]等，但若要達到理論精度，需要犧牲指數倍的運算量和采樣時間，對于工程應用非常不利。

上述兩種測量方法均以信號譜線作為頻率估計參數，沒有引入相位信息作為參數，文獻[1]分別給出了以信號譜線和相位兩種參數測量方法的克拉美羅下界，后者的估計下界遠低于前者。所以學者們開始對相位法測頻進行深入研究，Tretter最早利用回波信號的瞬時相位實現了頻率估計[11]，但在遠距離測量時存在相位模糊。為了避免這個問題，Kay提出一種基于采樣序列相鄰點相位差的估計方法[12]，但其對信噪比要求較高，于是Fitz提出了利用自相關函數相位的方法實現頻率估計[13]，這個算法降低了信噪比門限，但是測距范圍很小，沒有實際工程意義。文獻[14]針對這個問題提出了改進Fitz算法，將自相關函數的相位進行解纏，估計范圍擴大了M倍，且估計精度更高。文獻[15]提出了一種利用補零FFT細化頻譜的相位差測頻方法，精度更加逼近理論下界，但低信噪比時容易出現相位模糊。近年來基于相位差法的頻率估計算法不斷被提出[16-18]，但估計精度都不及文獻[15]。

綜上所述，比值法實時性強但頻率估計精度不足，頻譜細化的估計算法運算量過大，實時性不足，相位差法兼顧了精度和實時性的要求，但對信噪比條件要求較高。基于此，本文針對靜止目標的測距問題提出一種新的相位差改進算法，利用CZT消除相位模糊問題，再運用相位差法實現頻率估計。與以往相位差方法相比，大幅降低了運算量并在低信噪比條件下精度更高。

本文第一部分介紹了雷達測距技術的研究背景，第二部分推導了傳統相位差法測距的原理，第三部分給出了改進算法的原理和規避誤差的方法，最后在仿真中將它與經典算法對比，證明了該算法的性能優勢。

1 相位差法測距原理

線性調頻連續波雷達將發射信號與接收信號混頻，可以獲得需要我們研究的差拍信號。以單調頻斜率信號為例，雷達發射信號為

(1)

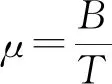
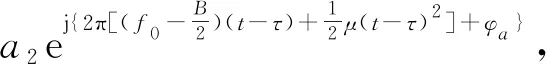
τ≤t≤T+τ

(2)

式中，τ=2r/c為延遲時間。兩個信號進行混頻，在實際應用環境中，τ數值很小，故混頻計算后可以忽略τ2項。得到差拍信號

(3)

由于τ?T，后續計算可以忽略τ，所以差拍信號的定義域可以記為0≤t≤T。根據式(3)，信號頻率fc由相位求導獲得，fc=μτ，所以距離和頻率的關系為r=cTfc/2B。

對差拍信號進行N點復采樣，采樣間隔T/N，無失真采樣需滿足奈奎斯特復采樣定理，即采樣頻率fs=N/T≥fc，所以最大探測距離r≤cN/2B，得到離散信號表達式：

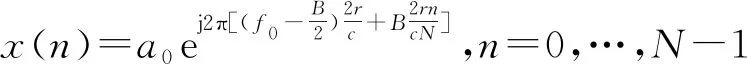
(4)

對其進行N點FFT變換，則距離分辨率ΔR=c/2B，變換后的表達式為

k=0,…,N-1

(5)

真實信號的頻譜在k取最接近2Br/c的整數k0時幅值最大，最大值處的相位為

(6)

(7)

所以真實值與量化頻點參考相位的相位差φr0=φk0-φk0， 距離估計就可以表示為

(8)

上述就是相位差法測距的過程，但是計算時忽略了相位模糊的問題。我們可以計算得到相鄰譜線相位差Δφk0>2π，所以計算距離偏移量時會出現模糊，需要細化頻譜使Δφk0<2π，從而消除模糊問題。

頻譜細化的主流算法有3種，補零FFT、Zoom-FFT和CZT(Chirp-Z)。文獻[16]就是利用補零FFT變換細化頻譜后消除了相鄰譜線的模糊，但其計算量較大且沒有考慮誤差導致的間隔譜線之間的相位模糊，所以在低信噪比條件下效果較差。Zoom-FFT所需要的原始數據較長，在工程瞬態過程中無法應用。CZT算法在Z平面對信號抽樣細化，具有運算量小、實時性高的優點，但還沒有學者利用CZT變換細化頻譜后再運用相位差法實現距離測量，所以本文對這個方法進行深入研究。

2 基于CZT變換的改進相位差算法

CZT變換即將序列x(n)(0≤n≤N-1)沿Z平面的一段單位圓作等分角的抽樣zk=AW-k(k=0,…,M-1),其中，A=A0ejθ0，W=W0e-jφ0，作CZT變換時A0=1,W0=1，θ0是起始采樣角度，φ0是兩相鄰采樣點之間的角度[19]，設CZT細化倍數是δ，則抽樣點在Z平面的周線如圖1所示。

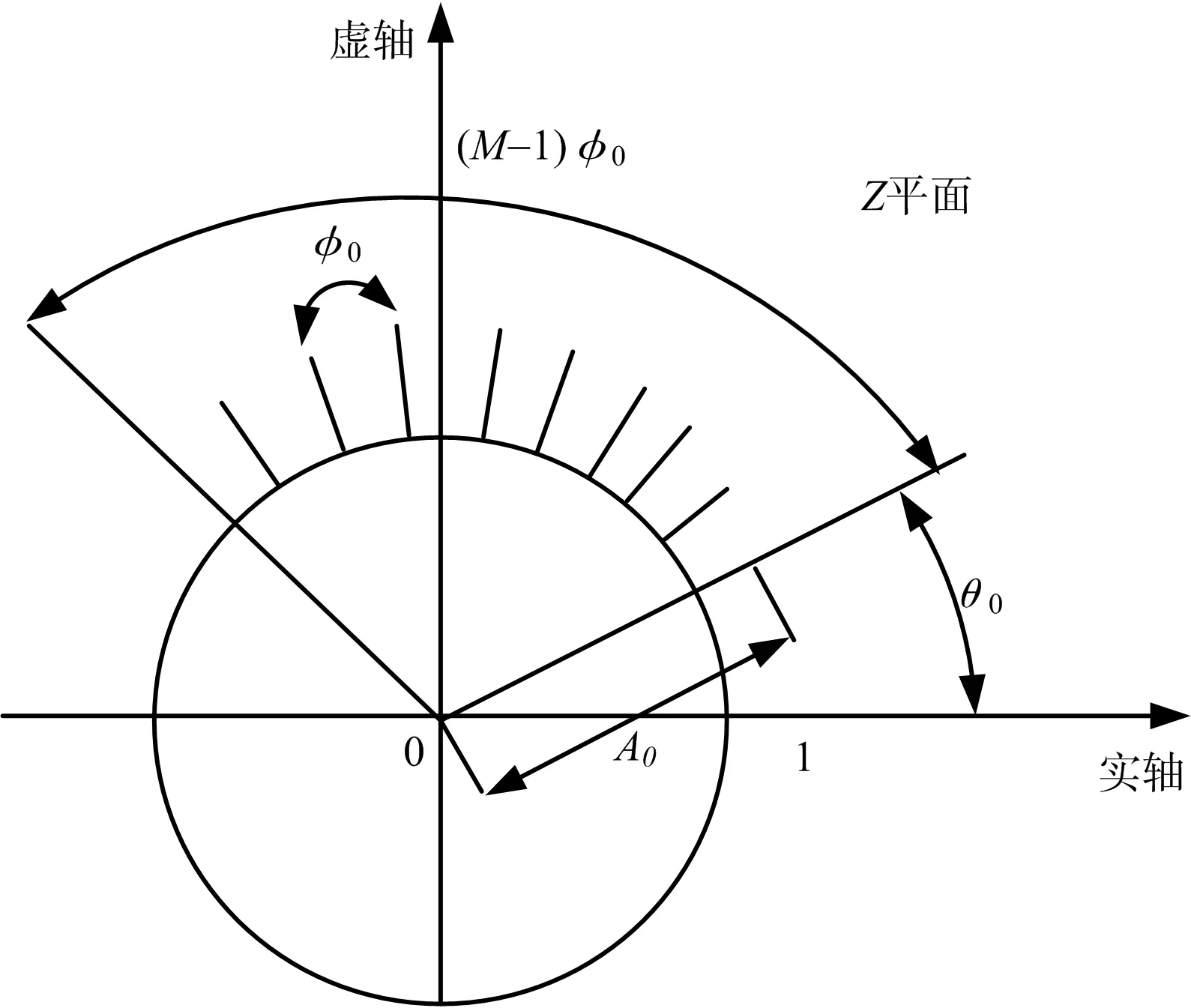
圖1 CZT變換在Z平面抽樣點的螺線軌跡

原信號的CZT變換表示為

(9)

(10)

由公式(5)可知，N點FFT后信號最大譜線的下標為k0，則θ0=2π(k0-1)/N，φ0=4π/MN，代入式(8)得

(11)

當r處于量化距離m1ΔR+m2Δr時(m2<δ)，參考相位為

(12)

式中，γ=δm1+m2。

當真實值偏移量化距離時，偏移值φr=φzk-φzk，則距離估計為

(13)

該算法利用CZT變換使頻譜細化了δ倍，完成了相鄰譜線相位去模糊的功能，但還需要進一步改進以獲得低信噪比條件下更好的測量效果。

在低信噪比環境下，信號最大譜線位置可能發生偏移，產生誤差。這時，我們會把第二大譜線m′2=m2±1當成m2來計算。當距離為r時，第二大譜線的相位為

而當r=m1ΔR+m′2Δr時，參考相位為

其中γ′=δm1+m′2。所以譜線偏移后計算得到的相位差為

(14)

將該結果計算距離，可以得到

(15)

理論上，即使噪聲導致最大譜線位置偏差，還是可以獲得正確的距離，但前提條件是上述相位值都是未解纏的，否則會出現模糊。例如φr-Δφzk<-π,m′2=m2+1時，計算得到的是解纏后的相位值，在-π～π區間，此時φ′r=φr-Δφzk+2π，這樣就出現了Δr的誤差。

為了避免這種情況，則必須滿足下式：

(16)

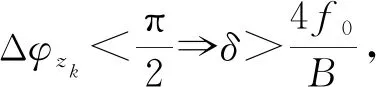
3 改進算法性能分析

3.1 改進算法與經典算法精度對比

采用Monte Carlo計算機模擬方法，對單一頻率的有噪聲差拍信號進行采樣，運用改進Fitz算法、補零相位差算法、本文算法進行仿真，仿真參數如表1所示。

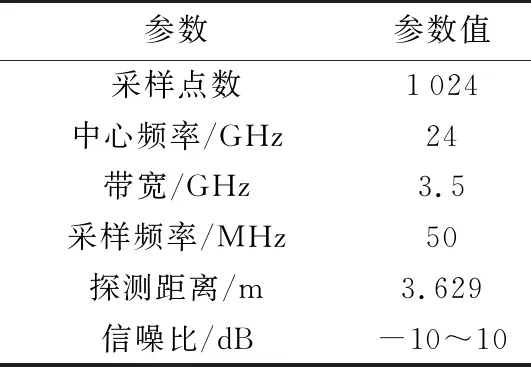
表1 仿真參數

在不同信噪比條件下對不同算法進行仿真并利用如下公式計算歸一化均方根誤差。

(17)

所得結果如圖2所示。

圖2 各算法不同信噪比誤差

圖2表明改進后的Fitz算法在高信噪比條件下精度比相位差算法低一個數量級。補零相位差算法精度較高但信噪比門限也高，為1 dB左右，改進的相位差算法精度最高，抗噪聲性能也最好，信噪比門限比補零相位差算法降低了7 dB。

3.2 改進算法與經典算法計算量對比

1) 改進Fitz算法

對N/2點信號作自相關運算，需要3N2/8次復乘，忽略復加運算。

2) 補零相位差算法

對輸入信號作8N點FFT運算，需要4Nlog28N次復乘。

3) 基于CZT的相位差算法

對輸入信號作CZT變換，使用基-2FFT法計算，M為細化點數，N為粗傅里葉變換點數，L為圓周卷積長度，L≥M+N-1，且L=2m(m為正整數)，則復乘次數為Llog2L+L+N+M[19]。

各算法計算量對比如表2所示。

表2 不同算法所需計算量對比

可見改進Fitz算法的計算量遠大于相位差算法，而CZT相位差算法又在補零相位差基礎上減少了一倍以上計算量，點數越多減少量越大，其優勢是顯而易見的。

4 結束語

本文針對相位差法信噪比門限高的問題，研究了低信噪比條件下誤差產生的原因，引入CZT算法，提出了能夠避免由于誤差導致的間隔譜線之間的相位差計算模糊的算法，提高了整體的抗噪聲性能，降低了運算量。新算法在仿真中驗證了其估計精度、抗噪聲性能等方面較經典相位差算法都有較大改善，實現了低信噪比條件下的高精度距離估計，對實際工程應用有重要意義。