含旋轉部件的動態目標ISAR成像及微多普勒特征提取*

趙東濤， 黃雁飛， 齊玉濤

(1. 中國飛行試驗研究院， 陜西西安 710089； 2. 中航西飛民用飛機有限責任公司， 陜西西安 710089)

0 引言

在逆合成孔徑雷達(ISAR)成像時，通常假設目標滿足剛體模型，即認為目標上所有散射點運動狀態是相同的。但是，對含有微動特征信息的目標，相對于主體部分存在高速旋轉, 由于不滿足剛體假設條件，其旋轉部件將在圖像中表現為沿多普勒方向的調制干擾，造成目標主體成像模糊[1-2]。為獲得目標完整、準確的成像特征描述信息，需要根據回波特征對旋轉部件和目標主體回波分離，一方面可以提高二維成像中目標主體結構的成像質量，獲得目標的精細結構特征信息[3],另一方面可提高微多普勒信號的微動參數估計精度，反演目標的運動和結構信息，作為目標識別的重要依據[4]。

Chen提出微多普勒概念以來，許多有效的微多普勒信號分離技術相繼被提出。小波變換分離活動部件及目標，通過剔除活動部件對成像結果的影響，提取清晰的散射中心，但是小波變換是一種時頻面上機械的格型分解，其本質上無自適應性[5]；基于Chirplet 基分解的分離方法，依據調頻率參數的大小對微多普勒信號進行分離，該方法對噴氣式飛機實測數據處理，取得了不錯的分離結果，但是，Chirplet 基函數包含4 個未知參數，分解算法運算量較大[6]；基于Radon變換的目標主體信號與微動信號分離方法，對回波信號進行時頻變換，然后在時頻平面上通過Radon變換來分離目標主體信號與微動信號，該方法對仿真數據取得較好的分離結果，但是對實測數據效果不明顯[7]。

本文利用目標主體信號穩定、多普勒頻率慢變化，而旋轉部件信號非平穩、多普勒頻率快變化的特性，采用時頻分析的技術將信號的時頻分布在時間維上按模值大小重新排列，設置門限剔除模值大的元素，從而將非平穩信號剔除,實現主體和微動信號的分離。但是在剔除非平穩信號過程中難免有主體回波損失，針對該情況，文中采用循環自適應的方式進行多次迭代，當剩余信號的總能量低于一定門限時迭代停止，認為剩下的成分就是目標主體的回波，從而實現目標主體回波和旋轉部件回波的分離。通過將旋轉部件回波和目標主體回波分離，可以提高目標主體的成像質量，對微動信號作單獨分析，能更好地獲得旋轉部件的微動特征參數[8-9]。

1 含旋轉部件目標回波成像模型

含旋轉部件目標ISAR成像轉臺模型示意圖如圖1所示，假定目標主體的平動已經補償并轉化為轉臺模型，xoy和x′o′y′分別為剛體目標和旋轉目標的坐標系，剛體散射點A(xA,yA)圍繞剛體坐標系原點O作角速度為ω0的勻速旋轉運動，旋轉目標散射點B(xB,yB)除了繞轉臺中心作角速度為ω0的勻速旋轉，還圍繞旋轉目標坐標系原點O′以自轉角速度ω′0作勻速旋轉運動，兩種轉動的角速度關系ω′0?ω0。

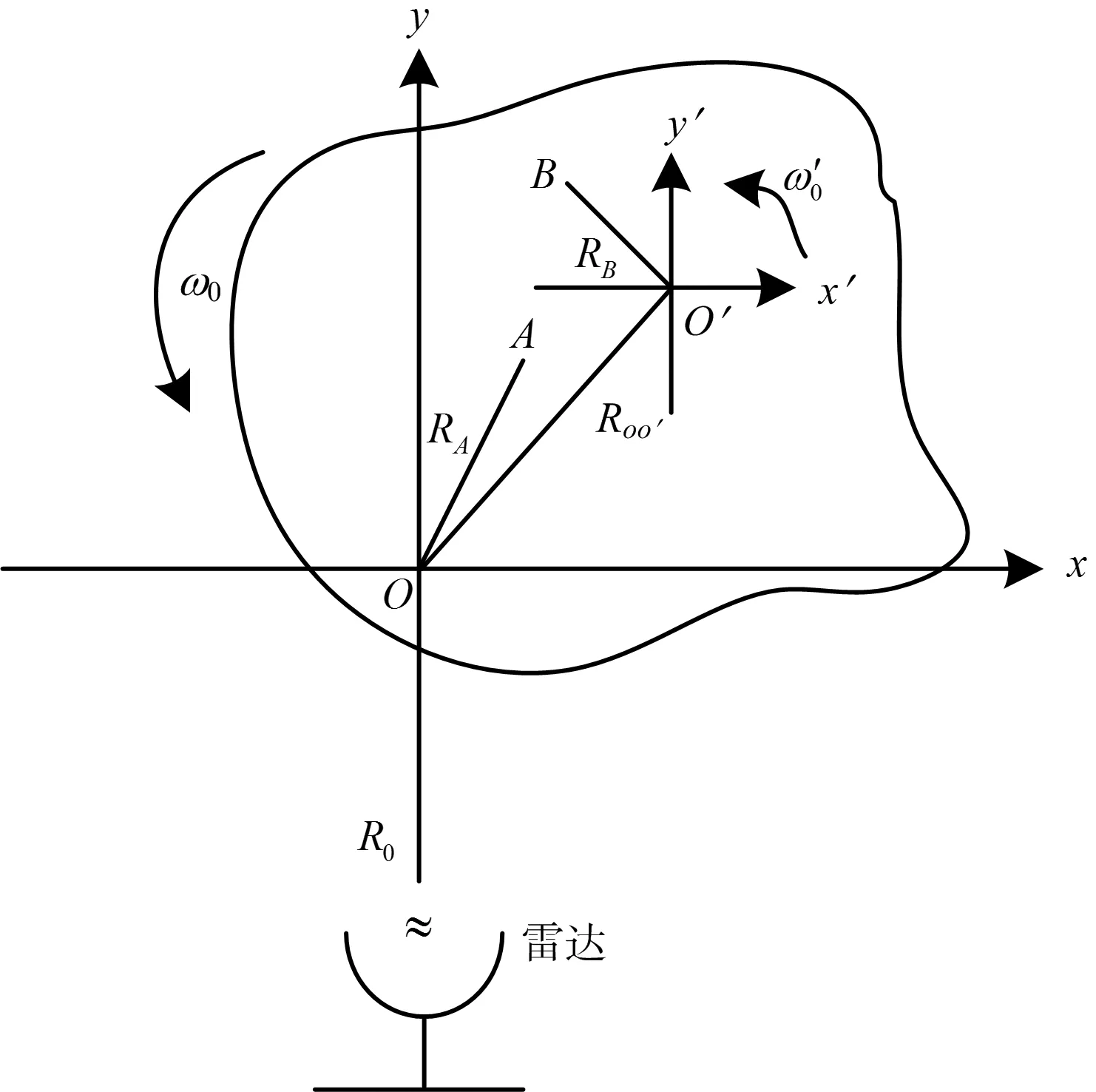
圖1 含旋轉部件ISAR轉臺模型示意圖

設雷達發射的線性調頻信號如式(1)所示：

(1)

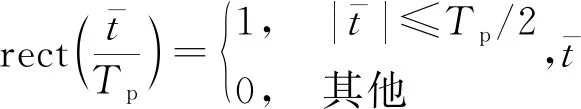
目標上第i個散射點的回波如式(2)所示：

(2)

式中，σ(tm)為目標后項散射系數，c為光速。以坐標原點O為參考距離構造參考信號如式(3)所示：

(3)

采用解線性調頻(Dechirp)信號處理方法，即

(4)

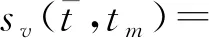
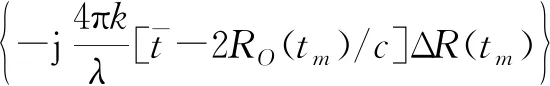
(5)

式中，λ為波長，ΔR(tm)=R(tm)-RO(tm)。

在快時間域對Dechirp處理之后的信號進行距離壓縮，可得如式(6)所示：

sv(f,tm)=σ(tm)Tp·

(6)

剛體散射點A和坐標原點O之間距離滿足：

ΔRA(tm)=RAsin(ω0tm)

(7)

由于RO O′?RO和RB?RO，旋轉部件散射點B和坐標原點O之間的距離如式(8)所示：

ΔRB(tm)=RO O′sin(ω0tm)+RBsin(ω′0tm)

(8)

2 基于時頻分析的微動特征信號分離算法

微動特征信號分離算法思路是利用主體回波信號穩定、多普勒頻率慢變化，而旋轉部件回波信號非平穩、多普勒頻率快變化的特性，采用時頻分析技術去除微多普勒效應的方法，實現機身主體回波和機翼旋轉部件回波的分離。具體步驟如下：

步驟1： 將包絡對齊后回波數據按距離單元存儲構成二維矩陣，行為同一距離單元不同發射脈沖的回波，列為每一個發射脈沖按距離單元存儲的回波；

步驟2： 每個距離單元作短時傅里葉變換(STFT)如式(9)所示：

(9)

式中，ω(i)為窗函數，k表示第k個距離單元，對于固定的頻率Ω，考慮到含有M個元素的集合，即

Sk(m)={STFTk(m,Ω),m=0,1,…,M-1}

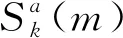
步驟4： 對于含有微動特征信息的STFT的變換結果按照模的大小重新排列，得到排列之后的結果：|φk(0)|≤|φk(1)|≤…≤|φk(M-1)|；

步驟5： 取固定的門限值Q%(Q一般取10～15)，采用循環自適應的方式進行多次迭代，剔除STFT中幅度較大的值，保留單頻信號；

步驟6： 將各個距離單元剩下的元素沿著時間軸進行累加，得到去除微多普勒效應后的剛體散射點的頻譜。微動特征信號分離流程如圖2所示。

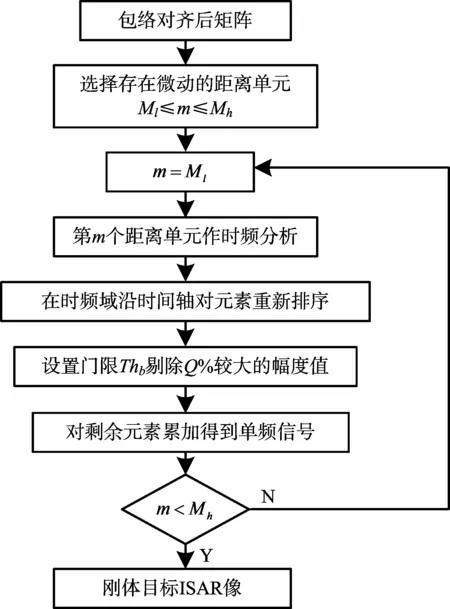
圖2 微動特征信號分離流程圖

3 微動信號分離后特征提取方法

由于旋轉部件微動具有周期性的簡諧振動，周期性的旋轉導致雷達回波調制亦具有周期性，因此可利用回波相關法估計旋轉部件微動的周期和頻率。假設旋翼葉片回波s(t)的離散表示為s(n)，其中n=1,2,…,N表示時域回波第n個時間點，N為時域回波信號點數，則回波自相關如式(10)所示：

(10)

由函數相關特性可知，R[m]在回波周期的整數倍處出現峰值，可反映回波的周期性，根據R[m]峰值之間的間距可以得到信號的周期估計結果，假設時間采樣間隔為Δt，那么周期估計結果表示如式(11)所示：

T=|m1-m2|Δt

(11)

式中，m1和m2分別表示相鄰兩個峰值的位置，則微動轉動頻率估計表示為F=1/T。

4 算法仿真分析

假設目標散射點模型由5個散射點組成，第1,2,3,4為主體射點，第5個散射點為主體散射點上附加旋轉散射點，旋轉頻率為25 Hz，散射點分布如圖3所示。設雷達發射線性調頻(LFM)信號，載頻為9.5 GHz，帶寬為1 GHz，脈寬為50 μs，脈沖重復頻率為1 kHz，成像積累脈沖數為512個。

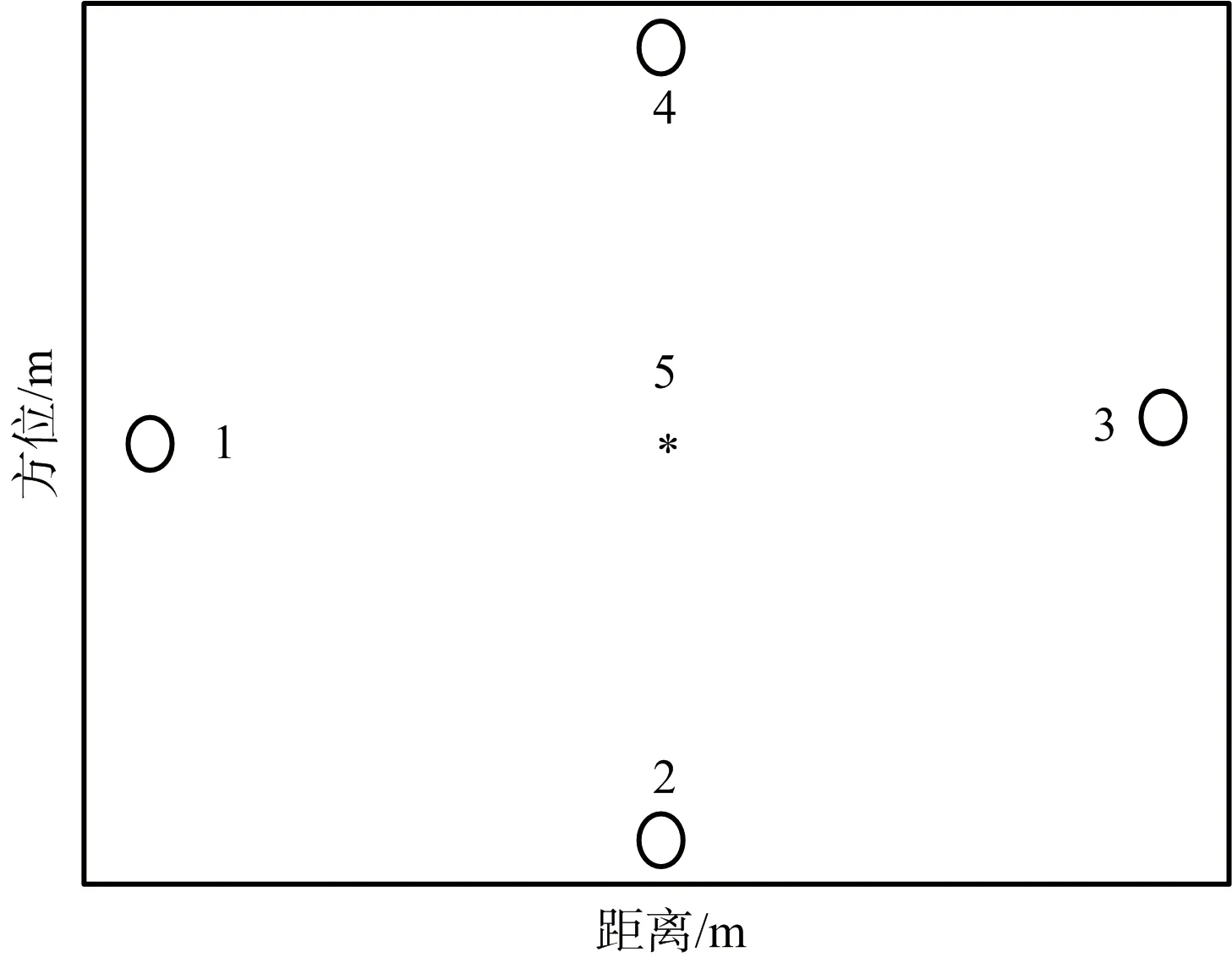
圖3 目標散射點分布示意圖

仿真過程中，向回波中加入高斯白噪聲，信噪比SNR=0 dB。對目標回波數據處理得到的ISAR 成像結果如圖4所示，從圖4可以看出，由于旋轉散射點5在第235個距離單元，該距離單元受到微多普勒調制的影響，使得主散射點1，3和5淹沒在調制帶中，掩蓋了主散射點。對該距離單元進行STFT得到其時頻圖如圖5所示，從圖5可以看出，回波信號的瞬時多普勒包含3條直線和1條正弦曲線，分別對應該距離單元內目標3個主體散射點和1個旋轉散射點。對該距離單元回波STFT后數據按照模的大小進行排列，分離STFT中幅度較大的值，保留單頻信號，實現旋轉部件成像和目標主體成像分離，分別如圖6和圖7所示。對分離后的微多普勒信號作自相關處理得到旋轉部件的旋轉周期，如圖8所示，此處求出旋轉周期為0.04 s，與旋轉頻率為25 Hz一致。

圖4 目標回波ISAR成像

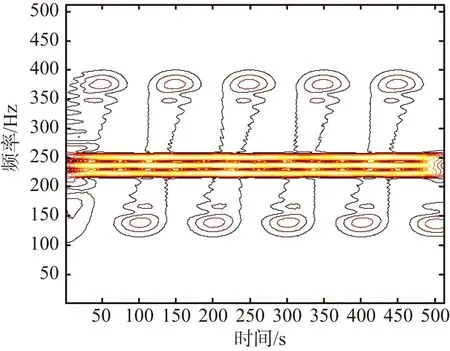
圖5 第235個距離單元回波的STFT

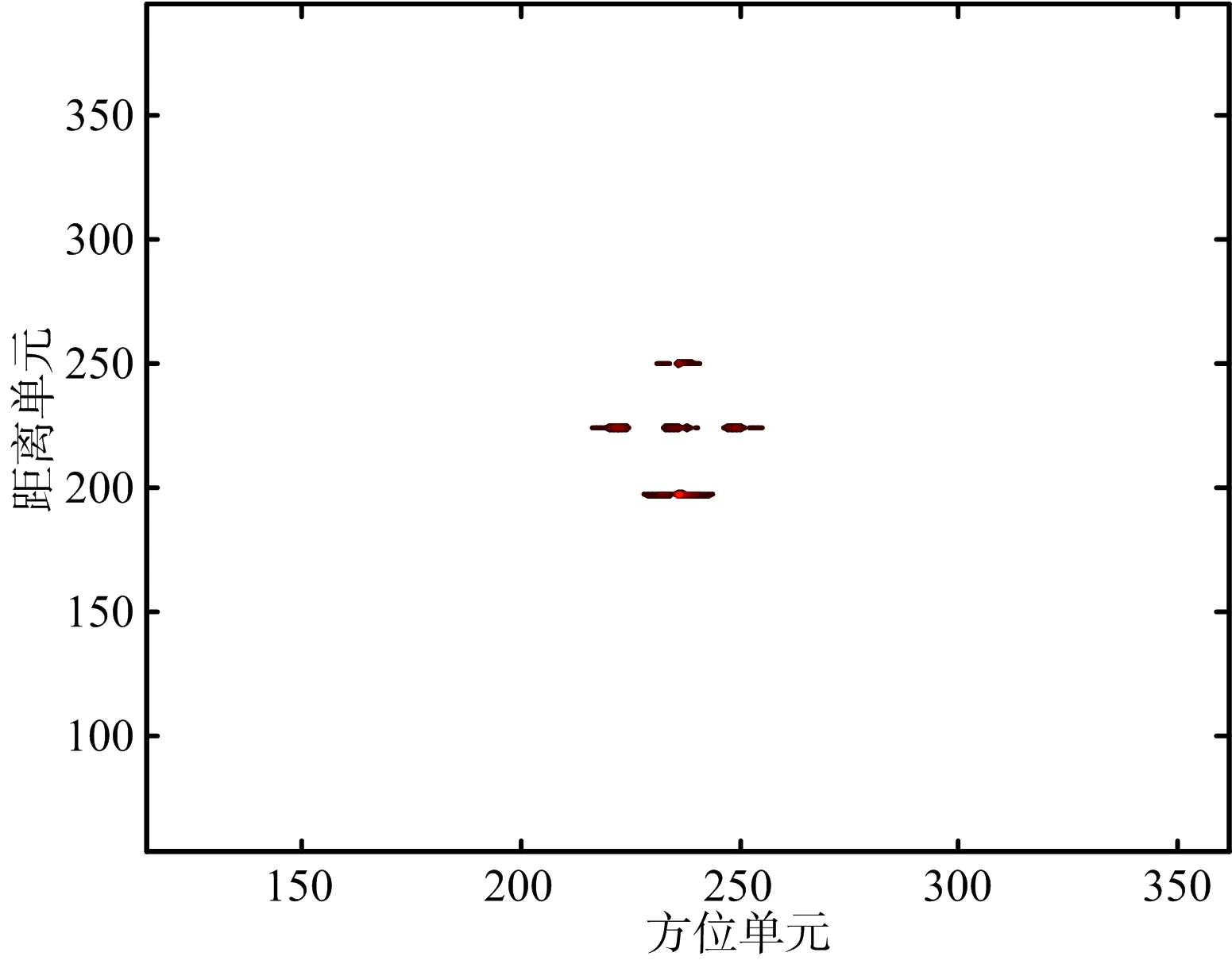
圖6 分離后目標主體部件的ISAR像

圖7 分離后目標旋轉部件的ISAR像

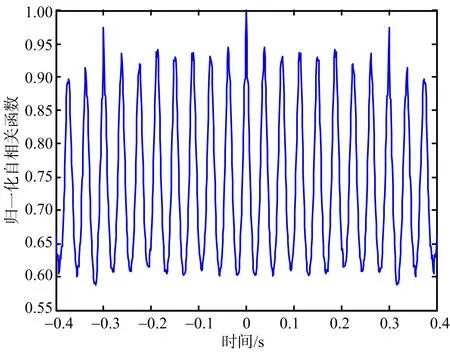
圖8 分離后第235個距離單元信號自相關

5 實測數據分析

以運七螺旋槳飛機雷達實測數據進行分析，驗證算法對實測數據的有效性。測量雷達工作在X波段，發射LFM信號，雷達載頻為9.5 GHz，帶寬為1 GHz，脈寬為50 μs，脈沖重復頻率為1 kHz，成像積累脈沖數為512。運七飛機實測數據ISAR圖像如圖9所示，從圖9可以看出，螺旋槳的旋轉帶來ISAR成像中的條帶干擾，由于螺旋槳相對于轉臺中心的角速度很大，無法將其散射點位置聚焦到方位的坐標，形成貫穿整個距離門的條帶，在第238個距離單元附近產生兩個展寬的微多普勒帶。采用上述方法對微多普勒信號和目標主體回波進行分離，分別如圖10和圖11所示，從圖10可以看出，去除微動信號后能夠清楚看到目標主體二維圖像，從圖11可以看出，分離出的微動信號調制頻率與目標ISAR圖像中的頻率一致，成功地實現了微動信號與主體信號分離。通過對比微多普勒分離前后的目標ISAR 像，可以看出，經該方法對實測數據進行微多普勒分離，能獲得聚焦的主體圖像。對第238個距離單元微多普勒信號分離前后的自相關函數分別如圖12和圖13所示，從圖中可以看出，分離前微動信號疊加在目標主體部分之上，微動特征不是很明顯，而分離后微特征信息比較明顯，與飛機實際螺旋槳調制周期一致。通過對比微多普勒分離前和分離后的目標ISAR 像及微多普勒特征信息，可看出該方法對實測數據微多普勒分離有效，可以獲得聚焦的主體圖像，且有利于更準確地估計出旋轉部件的微動參數，可用于不同類型飛機目標的分類和識別。

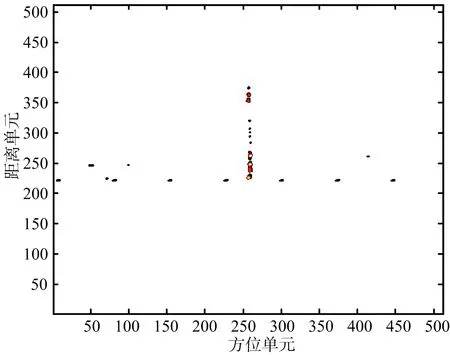
圖9 目標回波數據ISAR像

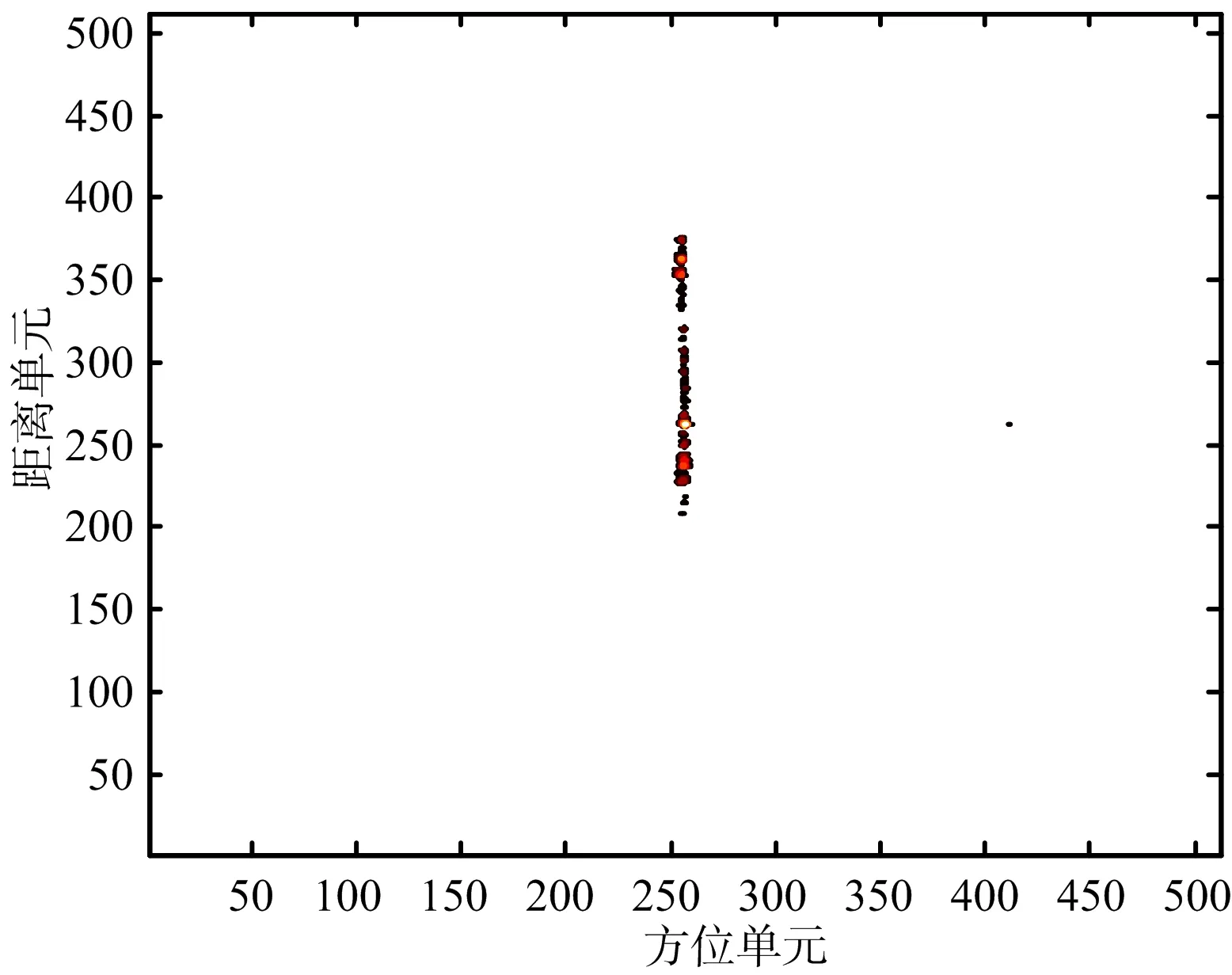
圖10 分離后目標主體部件的ISAR像

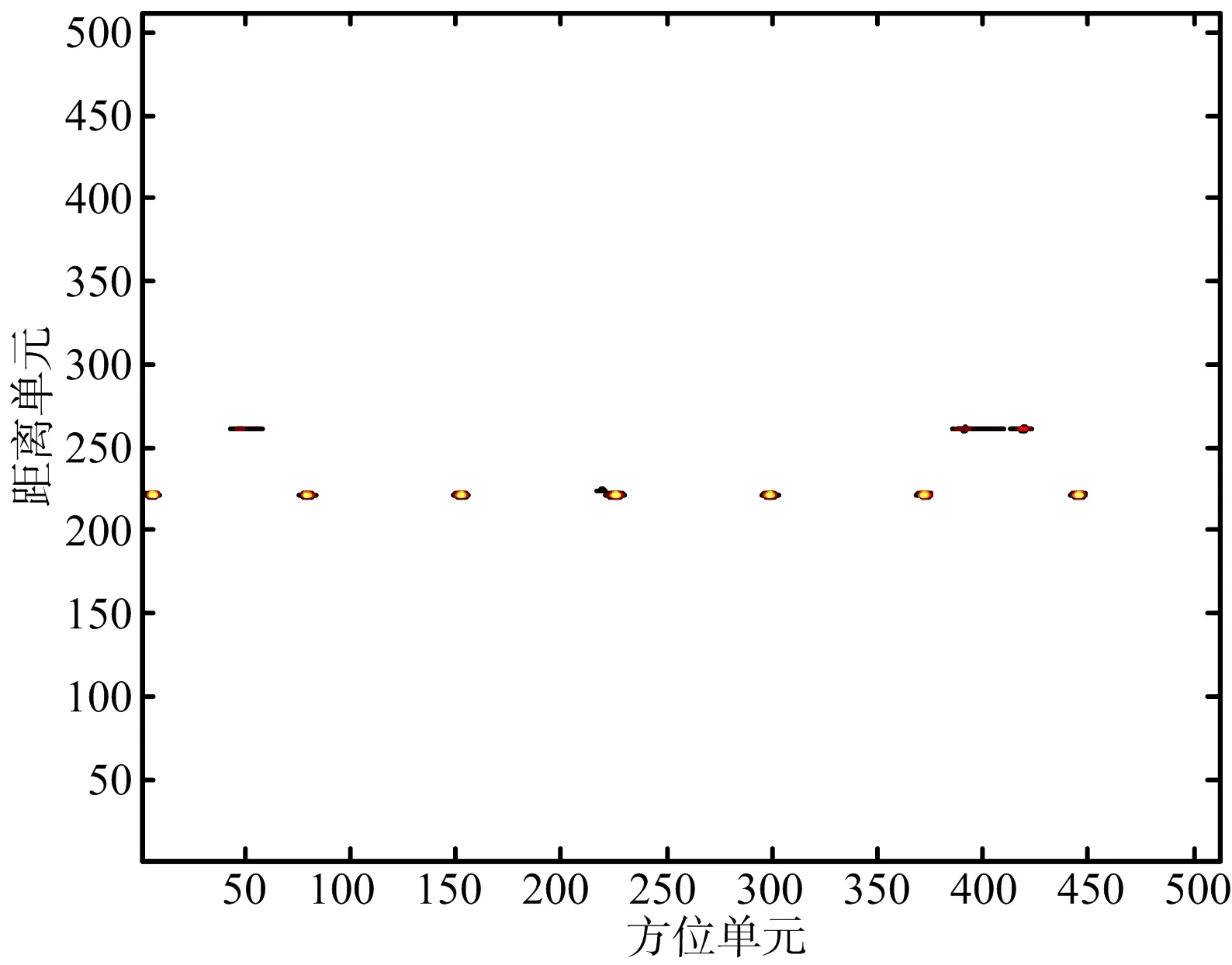
圖11 分離后目標旋轉部件的ISAR像

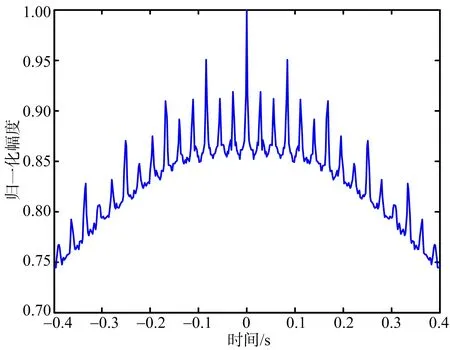
圖12 分離前第238個距離單元信號自相關

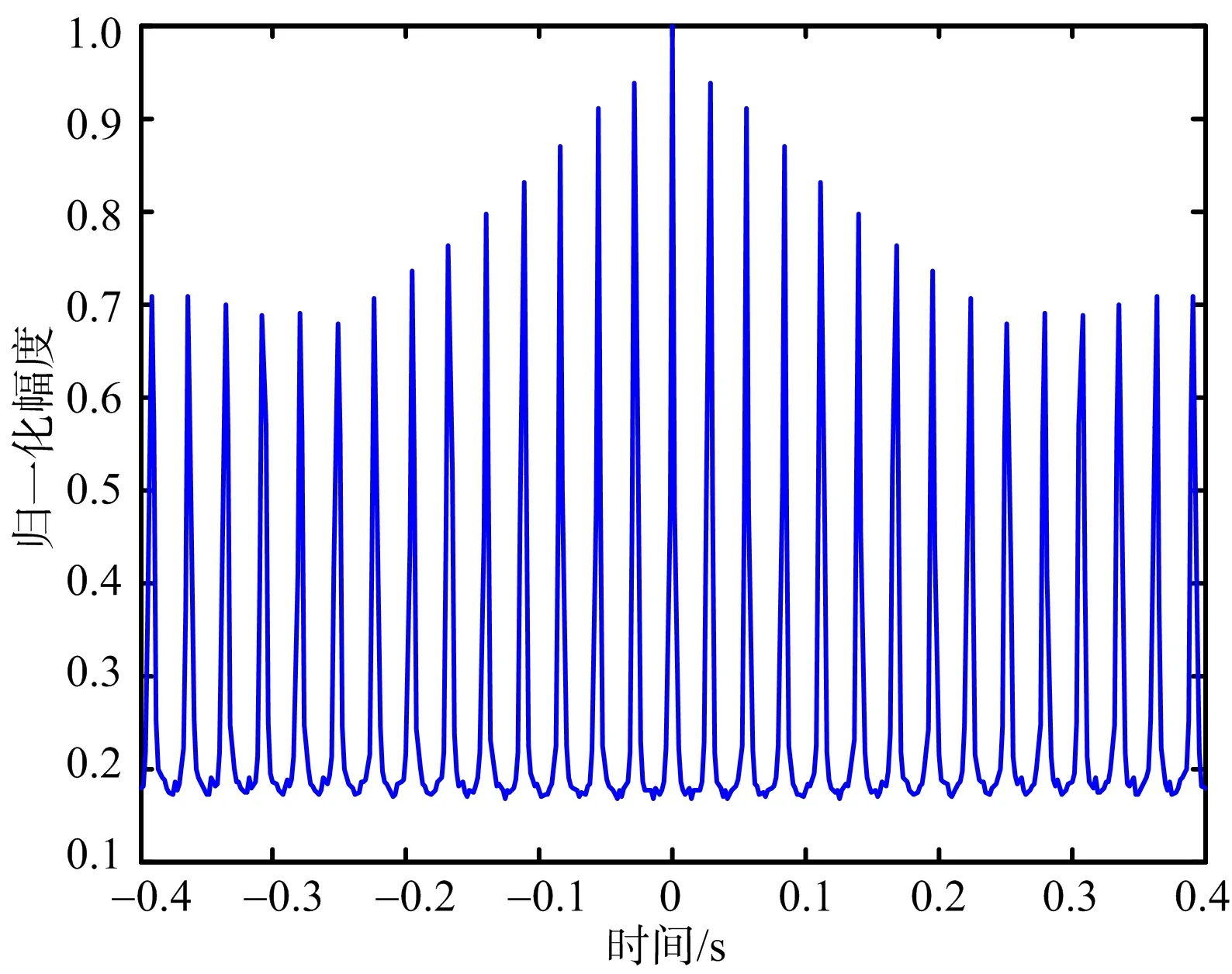
圖13 分離后第238個距離單元信號自相關

6 結束語

本文從含有微動特征信息的螺旋槳飛機目標的雷達實測數據中，獲得其二維逆合成孔徑雷達(ISAR)圖像，采用時頻分析技術分離出目標主體成像和微動部件成像，實現機身回波和主旋翼回波的分離，并對微動信號作單獨分析，更好地獲得旋轉部件的微動參數特征, 最后，通過仿真和實測數據驗證了本文提出算法的有效性。