磁懸浮雙轉子系統的定點碰摩特性

王東雄 王念先 陳奎生

1.武漢科技大學機械自動化學院，武漢，4300812.湖北汽車工業學院汽車工程學院，十堰，442002

0 引言

主動磁懸浮軸承(active magnetic bearing, AMB)是一種通過可控電磁力實現轉子穩定懸浮的新型軸承，具有無接觸、高轉速、高可靠性和支承特性主動可控等優點[1]，近年來在高速旋轉機械中的應用受到高度關注。為獲取高效率和高推重比，燃氣輪機、渦輪機和航空發動機等旋轉機械普遍將雙轉子結構作為其核心轉子部件。將雙轉子系統中的機械軸承替換為AMB將形成一個磁懸浮雙轉子系統，可顯著降低系統復雜度、減小質量、優化結構，獲得更高的可靠性和可維護性，大幅提高雙轉子系統的整體性能[2]。

隨著現代旋轉機械對高推重比和高功率密度的持續追求，轉靜部件之間的預留間隙更小、碰摩故障更易發生。碰摩是由不平衡、不對中、支座松動、油膜渦動和裂紋等故障引發的二次故障，輕者造成結構振動加劇、密封磨損、噪聲增大，影響機械使用壽命，重者將釀成慘烈事故[3]。為保證旋轉系統的穩定運行，需要研究磁懸浮雙轉子系統的碰摩特性。此外，為更合理地設計控制系統以發揮AMB支承特性主動可控的優勢，深入了解磁懸浮雙轉子系統碰摩故障下的振動特性至關重要。

根據接觸區域，碰摩可分為定點碰摩[4]、偏摩[5]和全周碰摩[6]。國內外學者從理論[7-8]、仿真[9-10]和試驗[11-12]等方面對單轉子系統在不同碰摩形式下的動態特性進行了深入研究。不同于單轉子系統，中介軸承的引入成為雙轉子系統的交叉激勵源，使得內外轉子之間的振動耦合加劇，導致雙轉子系統的動態特性更為復雜。考慮到接觸過程中圓盤和固定限位器端部表面敷涂層的軟化特性，YANG等[13-14]基于描述法向沖擊力的Lankarani-Nikravesh模型和表征摩擦特性的庫侖模型，建立了定點碰摩故障下的雙轉子系統動力學模型，分析了轉速比、初始間隙和限位器曲率半徑等參數對定點碰摩響應的影響，并在系統響應中觀察到內外轉子轉頻的組合頻率分量。可以看出，機械軸承支承的雙轉子系統的碰摩響應非常復雜，且明顯受軸承支承特性的影響，而磁懸浮雙轉子系統中AMB的支承特性不僅與軸承的結構參數有關，還與反饋控制系統及轉子的振動狀態等有關。轉子的動態響應通過機械系統和控制系統影響軸承的支承特性，使系統的碰摩響應發生變化，這種耦合效應將導致系統的動力學響應更加復雜。考慮到AMB的保護軸承與內轉子之間的接觸效應，EBRAHIMI等[15-16]基于拉格朗日方程建立了PD控制下磁懸浮雙轉子系統的十自由度動力學模型，分析了轉速比、重力、內轉子剛度和中介軸承剛度等參數對系統非線性動力學行為的影響。該動力學模型較為簡單，主要聚焦于系統的非線性動力學行為，未考慮雙轉子系統與機匣之間可能發生的碰摩故障。關于磁懸浮雙轉子系統碰摩故障下振動特性的詳細研究報道很少，而這對旋轉機械的穩定運行和故障診斷具有實際意義。

旋轉機械部件表面通常敷有各種涂層以延長使用壽命[17]。對于具有較軟涂層的轉靜碰摩，沖擊剛度并非由轉靜件的結構剛度決定，而是取決于涂層的局部接觸剛度(與涂層的材料性能和接觸區域的半徑有關)[18]。在這種情況下，Lankarani-Nikravesh模型[19]比分段線性模型[20]更適合描述涂層較軟的轉靜碰摩作用，已有學者進行了相關研究[13-14,21]。考慮到轉靜件表面涂層的軟化特性，筆者應用Lankarani-Nikravesh模型和庫侖模型分別對接觸過程中的法向沖擊力和摩擦特性進行描述，將PID控制下AMB支承特性等效為剛度阻尼模型，結合有限元法建立磁懸浮雙轉子系統定點碰摩故障下的動力學模型，并采用Newmark-β法求解，與文獻中試驗結果的對比驗證了動力學模型的有效性。最后，對定點碰摩故障下磁懸浮雙轉子系統的振動特性及接觸過程進行分析。

1 動力學模型

如圖1所示，磁懸浮雙轉子系統的內外轉子通過2個中介軸承連接，外轉子通過2個AMB實現懸浮支承。加載圓盤模擬實際雙轉子結構中的壓氣機盤或渦輪盤。外轉子左端和內轉子右端分別通過彈性膜片聯軸器連接2臺高速電機。根據實際需要，可調節2臺高速電機的旋轉方向，實現內外轉子的同向旋轉和反向旋轉。本文研究同向旋轉磁懸浮雙轉子系統的定點碰摩特性，為便于分析，對系統動力學建模過程做如下假設：①僅考慮徑向振動，忽略扭振及軸向振動的影響；②中介軸承簡化為線彈性支承；③AMB轉子熱套在外轉子轉軸上，將其與轉軸視為一個整體進行建模；④碰摩發生在圓盤3與固定限位器之間，且圓盤3和限位器敷有涂層，涂層的局部接觸剛度遠小于圓盤3和限位器的結構剛度；⑤碰摩時，忽略熱效應和摩擦力矩的影響；⑥系統不平衡量位于圓盤1和圓盤3上。

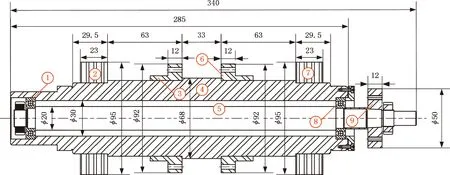
1.中介軸承 2.AMB轉子 3.圓盤2 4.外轉子 5.內轉子 6.圓盤3 7.AMB轉子 8.中介軸承 9.圓盤1圖1 磁懸浮雙轉子系統結構圖Fig.1 Structure diagram of magnetic suspended dual-rotor system

1.1 AMB支承模型

支承特性是AMB或機械軸承進行轉子動力學分析的基礎。相比于機械軸承，AMB系統開環不穩定，須采用反饋控制實現轉子懸浮。差動驅動模式的八磁極AMB豎直方向的基本控制回路和控制框圖見圖2。

(a)基本控制回路 (b)控制框圖圖2 AMB的基本控制回路和控制框圖Fig.2 Basic control loop and control blockdiagram of AMB

PID控制下，AMB的等效剛度ke和等效阻尼ce可表示為[22-24]

ke=kiAaAsKP-ks

(1)

ce=kiAaAs(KD-KI/ω2)

(2)

式中，KP、KI和KD分別為比例系數、積分系數和微分系數；Aa、As分別為功率放大器和位移傳感器的增益；ω為系統渦動頻率；ks、ki分別為AMB的位移剛度系數和電流剛度系數；μ0為真空磁導率；α為磁極對夾角的一半；Ap為磁極橫截面積；N為線圈匝數；Ib為偏置電流；g0為名義氣隙長度。

由式(1)可看出，AMB的等效剛度和等效阻尼同時取決于結構尺寸和控制系統，這表明在結構參數確定的情況下，AMB的支承特性可通過控制系統進行調整。考慮到AMB在X軸和Y軸的弱耦合效應，忽略等效交叉剛度和等效交叉阻尼。這樣，每個AMB可等效為2個相互正交且獨立的彈簧阻尼結構，從而可采用分散PID控制策略。

1.2 定點碰摩模型

考慮到轉靜部件表面所敷涂層的軟化特性，采用刻畫界面間局部變形的Lankarani-Nikravesh模型描述接觸過程中的法向沖擊力，采用庫侖模型描述摩擦力。如圖3所示，法向沖擊力Fn和切向摩擦力Ft分別為

(3)

Ft=frFn

(4)

式中，ce為恢復系數；fr為摩擦因數；kr為接觸剛度；μd、Ed、Rd分別為圓盤的泊松比、彈性模量和半徑；μp、Rp分別為固定限位器端部的泊松比和半徑；r為圓盤與限位器端部在碰撞方向上的距離；v為圓盤在碰撞方向上的沖擊速度；v0為初始沖擊速度。

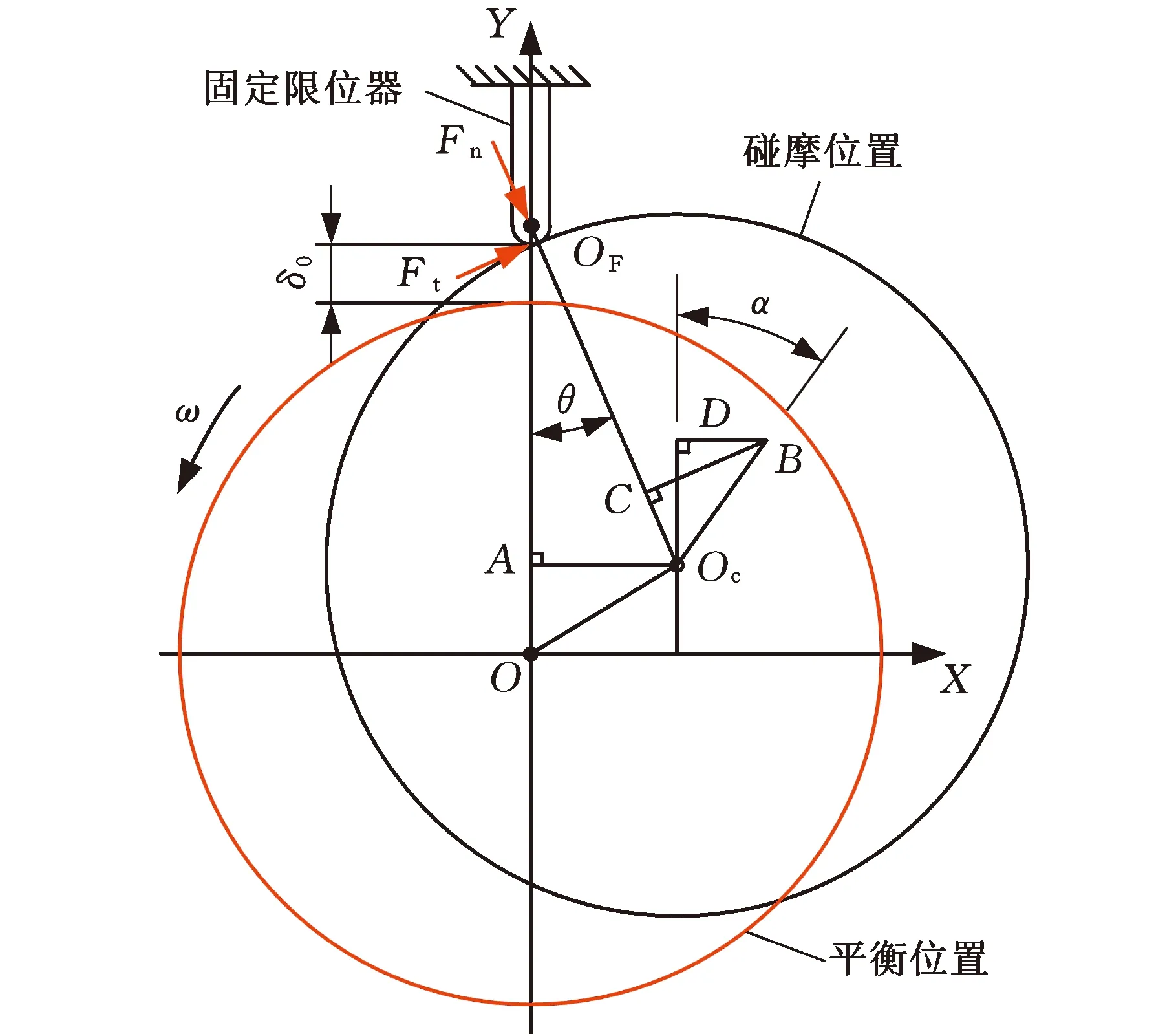
圖3 圓盤-固定限位器的碰摩力模型Fig.3 Rub-impact force model for disc-fixed limiter

若圓盤與限位器之間的初始間隙為δ0，圓盤中心Oc(x,y)和限位器端部中心OF(0,Rd+Rp+δ0)的連線與豎直方向之間的夾角為θ，則圓盤與限位器的中心距OcOF和r分別為

(5)

(6)

r>0表示發生碰撞。碰摩時的接觸角度為

(7)

圓盤中心的速度(vx,vy)與豎直方向的夾角為

α=arctan(vx/vy)

(8)

式中，vx、vy分別為圓盤中心的速度在水平方向和豎直方向的分量。

則由圖3可知圓盤在碰撞方向上的沖擊速度

(9)

在獲取r、v和v0的基礎上，由式(3)可得碰撞過程中的法向沖擊力Fn和摩擦力Ft，因此作用在圓盤上的碰摩力在水平方向和豎直方向的分量可分別表示為

(10)

由式(3)可知，初始沖擊速度v0直接影響法向沖擊力Fn的大小，因此準確確定碰摩發生的初始時刻、精確計算初始沖擊速度至關重要。本文采用線性插值法修正積分步長[25]，以提高計算精度。

1.3 系統動力學模型

根據圖1所示磁懸浮雙轉子系統的結構特點，采用Euler-Bernoulli梁單元模擬轉軸，將內轉子離散為11個軸段單元和12個節點，將外轉子離散為22個軸段單元和13個節點。為方便建模，將內外轉子上的3個圓盤視為剛性圓盤。系統有限元模型由圓盤單元、軸段單元和軸承單元組成，如圖4所示，圖中的坐標系為雙轉子系統建模過程中廣義位移(xk、yk、φyk、φxk)的參考坐標系。

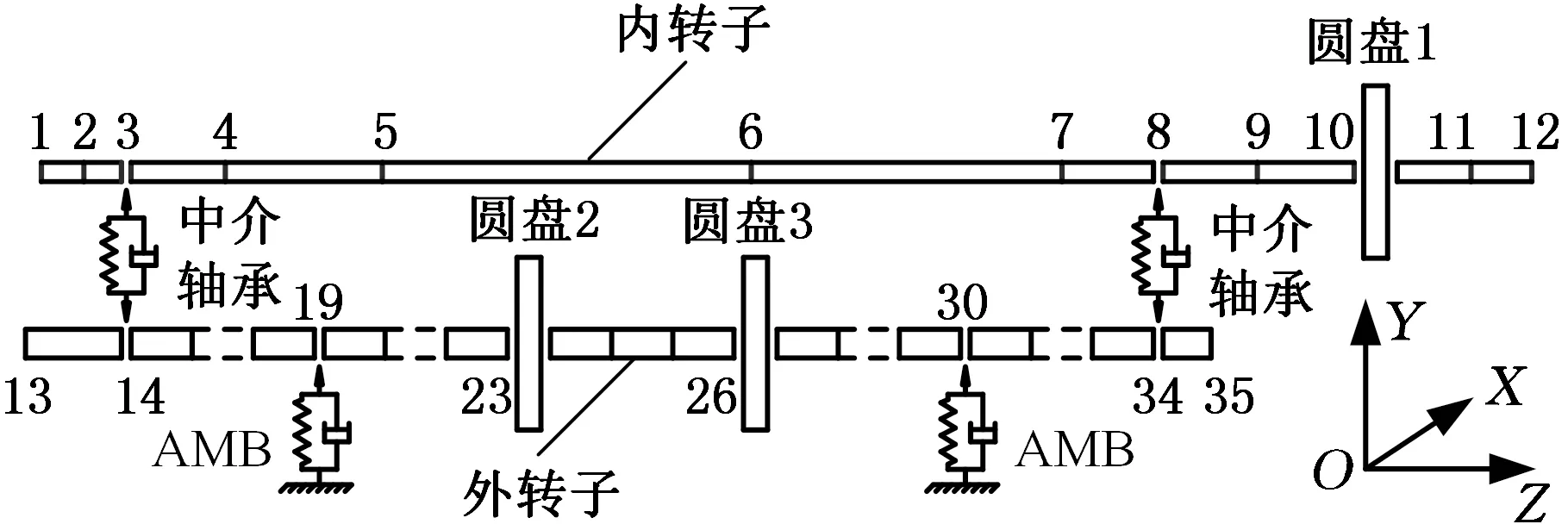
圖4 磁懸浮雙轉子系統的有限元模型Fig.4 Finite element model of magnetic suspendeddual-rotor system

各剛性圓盤單元、彈性軸段單元和軸承單元的運動方程可參考文獻[26]。由圖4設內轉子的廣義位移矢量為

(11)

式中，xk、yk(k=1, 2, …, 12)為內轉子節點k分別沿X軸和Y軸的平動位移；φxk、φyk為節點k分別繞X軸和Y軸的轉動位移。

通過組裝內轉子各軸段和圓盤的運動方程，可得內轉子在OXZ平面和OYZ平面的運動方程：

(12)

式中，Mi、Ji、Ki分別為內轉子子系統的質量矩陣、陀螺矩陣和剛度矩陣；ωi為內轉子的旋轉角速度；Q1i、Q2i分別為作用在內轉子子系統OXZ平面和OYZ平面的24×1階廣義力。

同理，設外轉子的廣義位移矢量為

(13)

式中，xk、yk(k=13, 14, …, 35)為節點k分別沿X軸和Y軸的平動位移；φxk、φyk為節點k分別繞X軸和Y軸的轉動位移。

外轉子在OXZ平面和OYZ平面的運動方程為

(14)

式中，Mo、Jo、Ko分別為外轉子子系統的質量矩陣、陀螺矩陣和剛度矩陣；ωo為外轉子的旋轉角速度；Q1o、Q2o為46×1階廣義力。

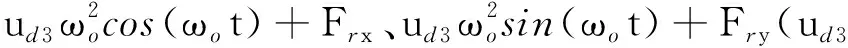
磁懸浮雙轉子系統的動力學方程可表示為

(15)

式中，0為零矩陣。

式(17)未考慮AMB和中介軸承的支承剛度與阻尼的影響。根據圖4所示AMB和中介軸承的節點編號，對系統剛度矩陣和陀螺矩陣進行修正[14]。在此基礎上，采用Newmark-β法獲取定點碰摩故障下的磁懸浮雙轉子系統動態響應。

2 動力學模型的驗證

采用上述動力學建模方法，建立圖5所示的雙轉子系統(參數見表1)的動力學方程，并將計算結果與試驗結果和仿真結果進行對比，以驗證建模方法的有效性。

圖5 雙轉子系統的有限元模型[13]Fig.5 Finite element model of Yang’s dual-rotor system

未碰摩情況下，內轉子旋轉角速度ωi=252.6 rad/s、外轉子旋轉角速度ωo=301.2 rad/s時，圓盤1在豎直方向的位移響應如圖6所示，從轉子的時域響應中可觀察到拍振現象，因為此時內外轉子的轉速比較接近[27]。本文仿真結果顯然與文獻[13]中的試驗結果一致。

表1 雙轉子系統主要參數[13]

(a)試驗結果[13]

根據文獻[13]，當內轉子旋轉角速度ωi=184.1 rad/s、外轉子旋轉角速度ωo=276.1 rad/s時，圓盤1在未碰摩情況下的響應頻譜只包含內外轉子的激勵頻率；在碰摩情況下，頻譜中除了內外轉子的激勵頻率外，還有ωo-ωi和ωi+ωo等組合頻率成分。本文仿真結果如圖7所示，響應頻譜也有上述特征頻率分量，只是各頻率分量對應的幅值有所不同，這是不平衡量位置和初始條件的差異導致的結果誤差。由上述分析可知，本文建立的定點碰摩故障下磁懸浮雙轉子系統的動力學模型是正確的。

圖7 雙轉子系統響應頻譜圖的仿真結果Fig.7 Frequency spectra of dual-rotor systemobtained by simulation results

3 磁懸浮雙轉子系統的定點碰摩特性分析

磁懸浮雙轉子結構的尺寸參數如圖1所示，系統其他參數如表2所示。為便于分析，定義外轉子旋轉角速度與內轉子旋轉角速度之比(即轉速比)rs=ωo/ωi。

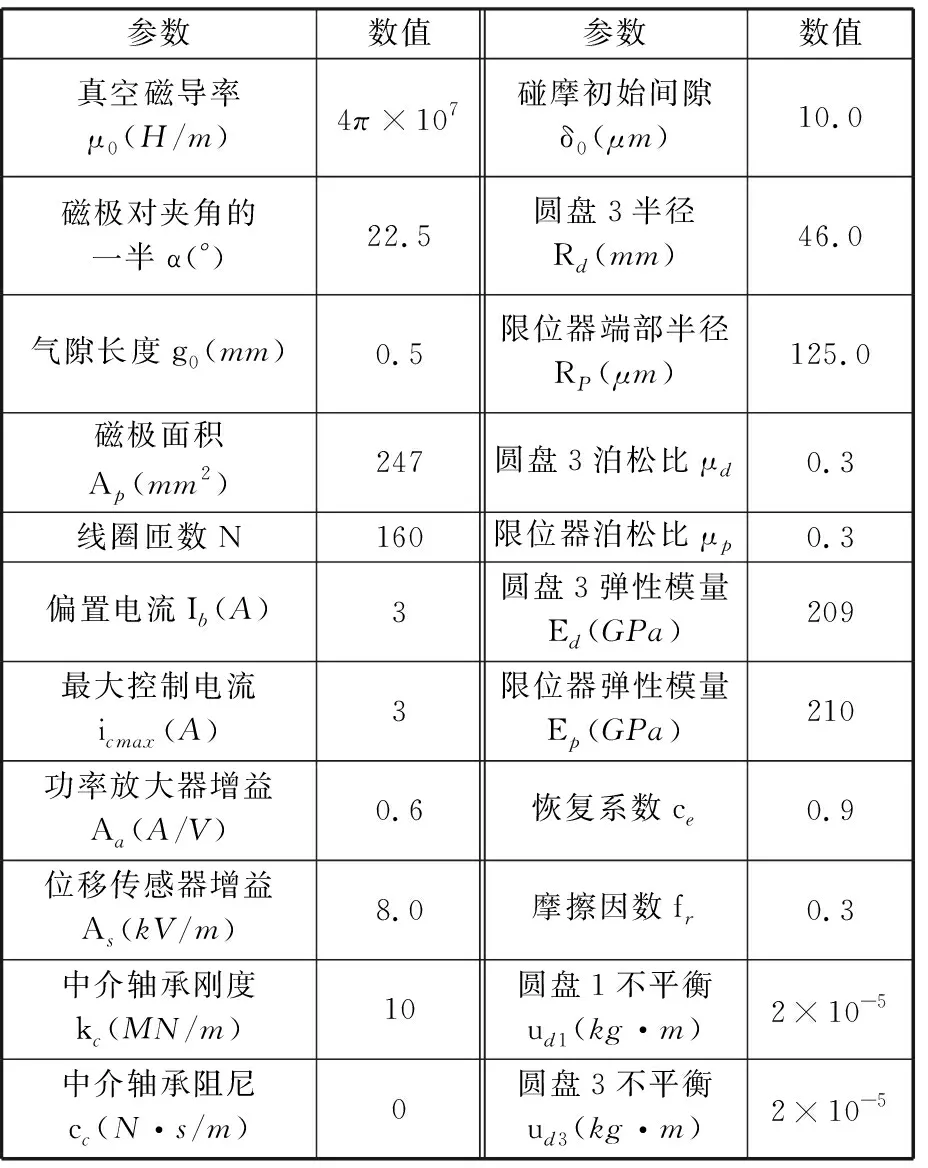
表2 磁懸浮雙轉子系統的主要參數

3.1 碰摩特性分析

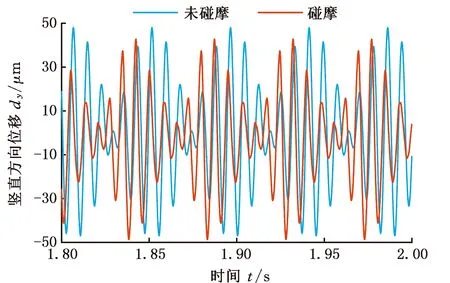
比例系數KP=5、微分系數KD= 5×10-4、積分系數KI=0、內轉子旋轉角速度ωi=700 rad/s、轉速比rs=1.2時，圓盤1和圓盤3的時域波形、軌跡和頻譜如圖8～10所示，圖中，“○”、“*”分別表示圓盤中心某一時刻和后續某一時刻的位置，據此判斷轉子的渦動方向；軌跡圖中的數字表示一個運動周期內圓盤依次發生碰撞的順序；圖9、圖10中的虛線所處位置表示碰摩的初始間隙。由于內外轉子的旋轉角速度較為接近，故從時域響應中可觀察到拍振現象，這與文獻[13,27-28]中所得出的結論是一致的。

(a)內轉子

(a)內轉子(未碰摩)

(a)內轉子

未碰摩時，內外轉子均做正向渦動，運動軌跡表現為相互交織的環，頻譜只包含內轉子轉頻(fi=111.5 Hz)和外轉子轉頻(fo=133.5 Hz)。碰摩時，內轉子軌跡為“花瓣”狀，外轉子軌跡為相互交叉的橢圓；在一個運動周期內的6次碰摩過程中，內轉子在過程3～6中做正向渦動，在過程1、2中做反向渦動，而外轉子始終處于反向渦動狀態。反向渦動下，轉子的軸向纖維承受交變應力，長期工作在這種狀態下的轉子很容易發生疲勞失效[29]。頻譜中出現17個等間距分布的頻率分量n(fo-fi) (n=1,2,…,17)，其中的第5、第6個分量分別表示內外轉子的轉頻。等間距頻率分量的出現主要是由于轉子徑向載荷在碰摩過程中發生變化，產生的碰摩力激發較寬的頻帶，且在中介軸承的耦合作用下，外轉子除了受本身不平衡激勵外，還受內轉子的不平衡激勵。這些復雜載荷的周期性激勵產生整數倍轉頻差頻率分量，進而形成峰值等間距分布的頻譜。

為深入了解定點碰摩情形下轉靜碰摩部件相互作用時的動力學特性，進一步分析轉子發生反向渦動的原因，有必要研究整個碰摩過程。Lankarani-Nikravesh模型中，一個完整的碰摩過程可分為壓縮階段和分離階段[19]。圖9顯示出了一個運動周期內圓盤在6次碰摩過程中的壓縮階段和分離階段(分別用藍線和紅線表示)。可以看出，圓盤在各碰摩過程中的起始接觸角度和接觸深度是不同的。圖11給出了一個運動周期內圓盤在碰撞方向的法向沖擊力、接觸深度、接觸角度(未接觸時角度設為零)和沖擊速度的變化過程，碰摩特征參數列于表3。

如圖11所示，在接觸過程的壓縮階段，法向沖擊力隨接觸深度從零逐漸增大，且與接觸深度同時達到最大值，而沖擊速度一直減小，直到0，隨后進入分離階段；在分離階段，接觸深度和法向沖擊力均從最大值減小為0，而沖擊速度從0一直增大。在接觸過程中參數的變化趨勢與Lankarani-Nikravesh模型中相應參數的變化趨勢一致[19]，這說明了本文所建系統碰摩動力學模型的合理性。在Lankarani-Nikravesh模型中，材料的阻尼導致碰撞過程中的部分能量損失，沖擊速度在接觸開始時刻的值大于結束時刻的值。由圖11b發現，沖擊速度在接觸開始的值并不總是大于結束的值，這是因為碰摩過程中，沖擊速度的大小不僅與圓盤的運動速度和方向有關，還取決于接觸角度。碰摩過程4～6中，接觸角度隨時間的推移表現出先增大后減小的趨勢，說明圓盤中心從左向右運動到最大接觸角位置后又向左運動，轉子處于運動方向急劇改變的位置區間。

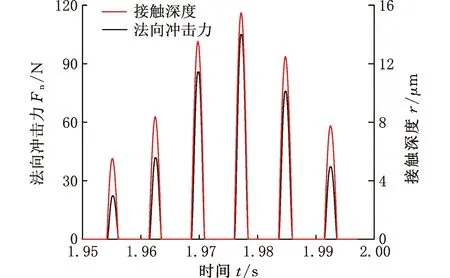
(a)法向沖擊力和接觸深度

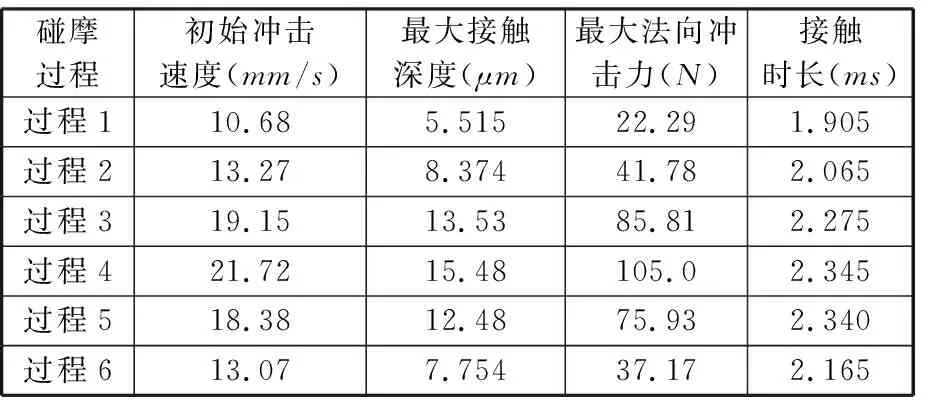
表3 磁懸浮雙轉子系統碰摩特征參數

由圖11、表3可看出，在一個運動周期內的6次碰摩過程中，最大法向沖擊力達到105.0 N，對應的摩擦力達到31.5 N(外轉子不平衡力幅值14.1 N的2.23倍)，故摩擦力取代不平衡力成為主導系統響應的主要載荷。摩擦力的方向總是與外轉子旋轉方向相反，驅動外轉子沿摩擦力方向運動，導致外轉子做反向渦動。在中介軸承的強烈動力耦合作用下，內轉子處于間歇反向渦動狀態。此外，碰摩過程壓縮階段開始時刻的初始沖擊速度決定了表征碰摩特征的最大接觸深度和最大法向沖擊力。初始沖擊速度越高，圓盤在沖擊方向上減速為零時所需的接觸深度越大，導致法向沖擊力越大。接觸時長不僅與接觸深度有關，還取決于圓盤在碰摩過程中的軌跡弧長。

圖12為外轉子圓盤3豎直方向動態響應的瀑布圖。0～350 Hz范圍內的19個頻率分量可分為兩部分：一部分為內外轉子轉頻的組合頻率分量(mfi±nfo；m,n=1,2,…)(圖12中藍線箭頭標注)，另一部分為分數階形式的組合頻率分量 (mfi±nfo)/2(圖12中紅線箭頭標注)。根據對不同轉速比下轉子動態響應瀑布圖的分析發現，當內外轉子的轉頻是其轉頻差的整數倍時，組合頻率分量mfi±nfo可表示為整數倍的轉頻差分量n(fo-fi)，分數階形式的組合頻率分量 (mfi±nfo)/2可表示為分數階形式的轉頻差分量n(fo-fi)/2，后者出現在系統的臨界角速度附近。轉速比rs=1.2時，各頻率分量對應的轉頻差表達式見表4。轉頻差描述因碰摩故障產生的響應頻率分量，可直觀地反映內外轉子之間通過中介軸承耦合作用表現出來的動力耦合現象，這是雙轉子系統碰摩響應與單轉子系統碰摩響應的主要區別。

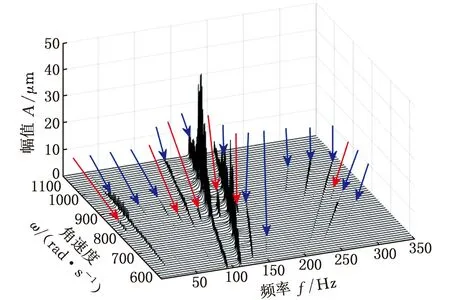
圖12 磁懸浮雙轉子系統碰摩響應瀑布圖(KP=5,KD=5×10-4,KI=0)Fig.12 Waterfall plot of rub-impact response formagnetic suspended dual-rotor system(KP=5,KD=5×10-4,KI=0)

表4 轉速比rs=1.2下組合頻率分量的轉頻差形式

圖13為內轉子圓盤1的分岔圖和ωi=700 rad/s時的Poincaré圖。未碰摩時，在圖13a中600～1000 rad/s范圍內，內轉子響應始終表現為周期5的次同步振動，此時，圖13b中Poincaré圖出現5個散點。碰摩時，轉子在805～845 rad/s范圍內表現為周期10振動，如圖13c所示，該范圍恰好在系統第一階臨界角速度828 rad/s附近，與圖12中分數階組合頻率分量出現的范圍一致，因此高階次同步振動的出現意味著碰摩程度的加劇。系統在其他轉速處表現為周期5振動，如圖13d所示，圖中出現5個散點。

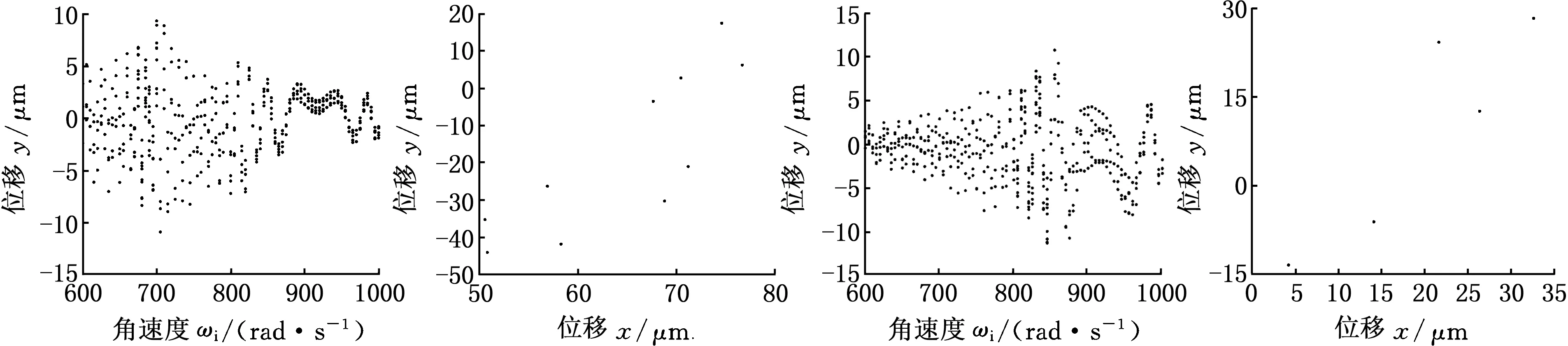
(a)未碰摩的分岔圖 (b)未碰摩的Poincaré圖 (c)碰摩的分岔圖(d)碰摩的Poincaré圖圖13 磁懸浮雙轉子系統分岔圖與Poincaré圖(KP=5,KD=5×10-4,KI=0)Fig.13 Bifurcation diagrams and Poincaré maps of magnetic suspended dual-rotor system(KP=5,KD=5×10-4,KI=0)

3.2 控制參數的影響

軸承的支承特性通常對轉子系統的動態響應有很大影響[30]。下面簡要分析在PID控制下，系統的碰摩特性隨AMB控制參數的變化規律。

由式(1)可知，比例系數可控制AMB的等效剛度，而等效剛度對系統的臨界角速度有很大影響。在KP∈{3，5}、KD= 5×10-4、KI=0、rs=1.2、其他參數與表2相同的情況下，系統前兩階臨界角速度如表5所示。KP=3、其他參數與3.1節示例相同時，系統的碰摩響應和接觸過程分別如圖14～17所示，角速度對轉子響應的影響見圖18、圖19。由表5可知，內轉子角速度ωi=700 rad/s與系統的第一階阻尼臨界角速度非常接近。對比圖10中KP=5時的碰摩響應，圖16的頻譜中不僅出現整數倍轉頻差頻率分量n(fo-fi) (n=1,2,…,17)，還含有分數階形式的轉頻差頻率分量n(fo-fi)/2 (n=1,3,5,…,35)，且整數倍轉頻差分量的幅值大于相鄰分數階轉頻差分量的幅值；最大法向沖擊力由圖11a的105.0 N增大到圖17a的138.6 N；分數階頻率分量從圖12中的6個增加至圖18中的8個；頻率分量出現的角速度范圍更寬，幅值增大，碰摩更為嚴重。這是因為轉子的運行角速度接近系統臨界角速度時，系統振幅較大，振動劇烈，導致圓盤發生碰摩時的沖擊速度較高、摩擦力較大，轉子將發生后向渦動，且頻譜中的頻率成分更為復雜，碰摩更為嚴重。因此，在強烈的碰摩激勵下，圖19a中臨界角速度附近670～700 rad/s范圍內發生高階次同步周期10振動，此時，圖19b中出現10個散點，而在其他范圍內表現為周期5振動。可見，比例系數對磁懸浮雙轉子系統的碰摩響應有重大影響。對PID控制的磁懸浮雙轉子系統而言，可通過改變比例系數的方法使系統的工作角速度遠離臨界角速度，從而避免發生嚴重的碰摩響應。

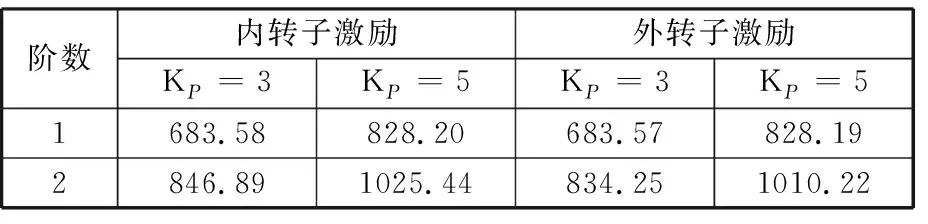
表5 磁懸浮磁懸浮雙轉子系統的前兩階臨界角速度

圖14 碰摩響應的時域波形圖(KP=3,KD=5×10-4,KI=0)Fig.14 Oscillogram of time domain for ru bbingresponses(KP=3,KD=5×10-4,KI=0)

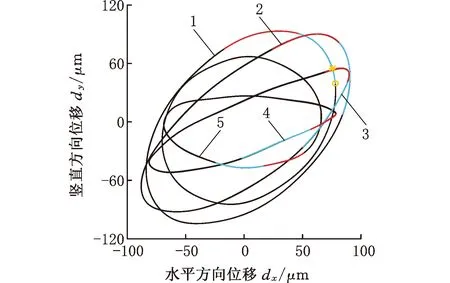
(a)內轉子

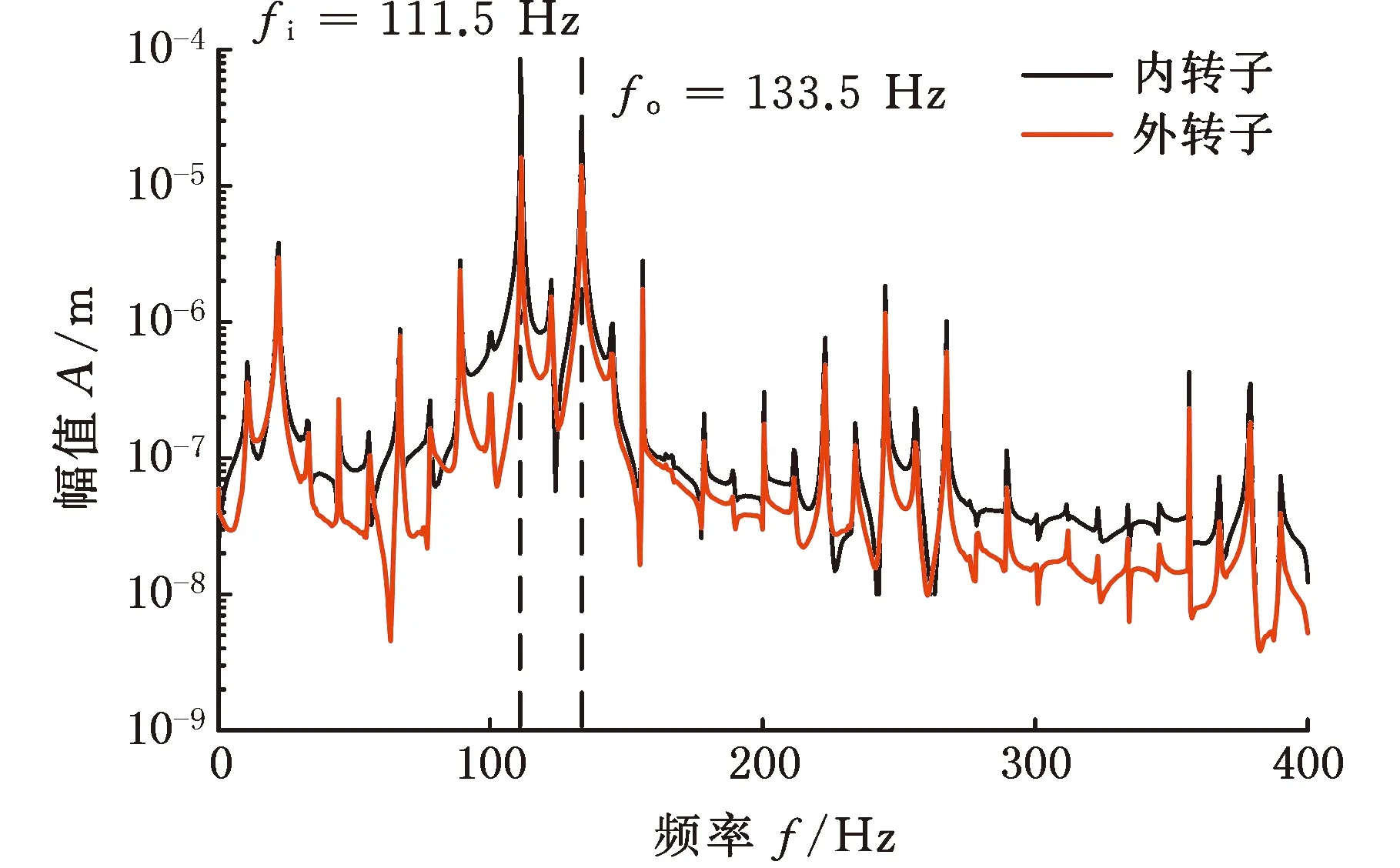
圖16 碰摩響應的頻譜圖(KP=3,KD=5×10-4,KI=0)Fig.16 Spectrogram of ru bbing responses(KP=3,KD=5×10-4,KI=0)

(a)法向沖擊力和接觸深度

圖18 磁懸浮雙轉子系統碰摩響應瀑布圖(KP=3,KD=5×10-4,KI=0)Fig.18 Waterfall plot of rub-impact response formagnetic suspended dual-rotor system(KP=3,KD=5×10-4,KI=0)

(a)分岔圖 (b)Poincaré圖圖19 磁懸浮雙轉子系統分岔圖與Poincaré圖(KP=3,KD=5×10-4,KI=0)Fig.19 Bifurcation diagrams and Poincaré maps ofmagnetic suspended dual-rotor system(KP=3,KD=5×10-4,KI=0)

根據式(1)，微分系數可改變AMB的等效阻尼。在KD=3×10-3、其他參數與3.1節示例相同的情況下，系統的碰摩響應及接觸過程如圖20～23所示，角速度對轉子響應的影響見圖24、圖25。對比3.1節中KD=5×10-4時的碰摩響應，一個運動周期內的碰摩從圖9d中的6次減少到圖21b中的2次；最大法向沖擊力從圖11a的105.0 N減小到圖23a中的7.0 N；圖24中僅出現整數倍的轉頻差分量，幅值大幅減小，碰摩程度減弱。因此，在圖25a的600～1000 rad/s范圍內，轉子始終做周期5振動。微分系數較小時，AMB提供的等效阻尼較小，抑制系統振動的能力有限，振幅較大，轉子的渦動軌跡較為復雜，內外轉子均處于反向渦動的狀態，頻譜中除整數倍轉頻差頻率分量和分數階轉頻差頻率分量外，可能還出現其他雜亂頻率成分。微分系數較大時，等效阻尼較大，一個運動周期內圓盤的碰摩明顯減少，碰摩過程中的最大接觸深度和法向沖擊力顯著減小，內外轉子均做正向渦動，頻譜中僅出現整數倍轉頻的差頻率分量。可見，選取較大的微分系數有助于減小振動、克服振蕩，降低碰摩的嚴重程度。通過AMB控制系統為雙轉子系統引入適量可控阻尼以實現減振增穩，這是磁懸浮雙轉子系統優于傳統雙轉子系統之處。

圖20 碰摩響應的時域波形圖(KP=5,KD=3×10-3,KI=0)Fig.20 Oscillogram of time domain for ru bbingresponses(KP=5,KD=3×10-3,KI=0)

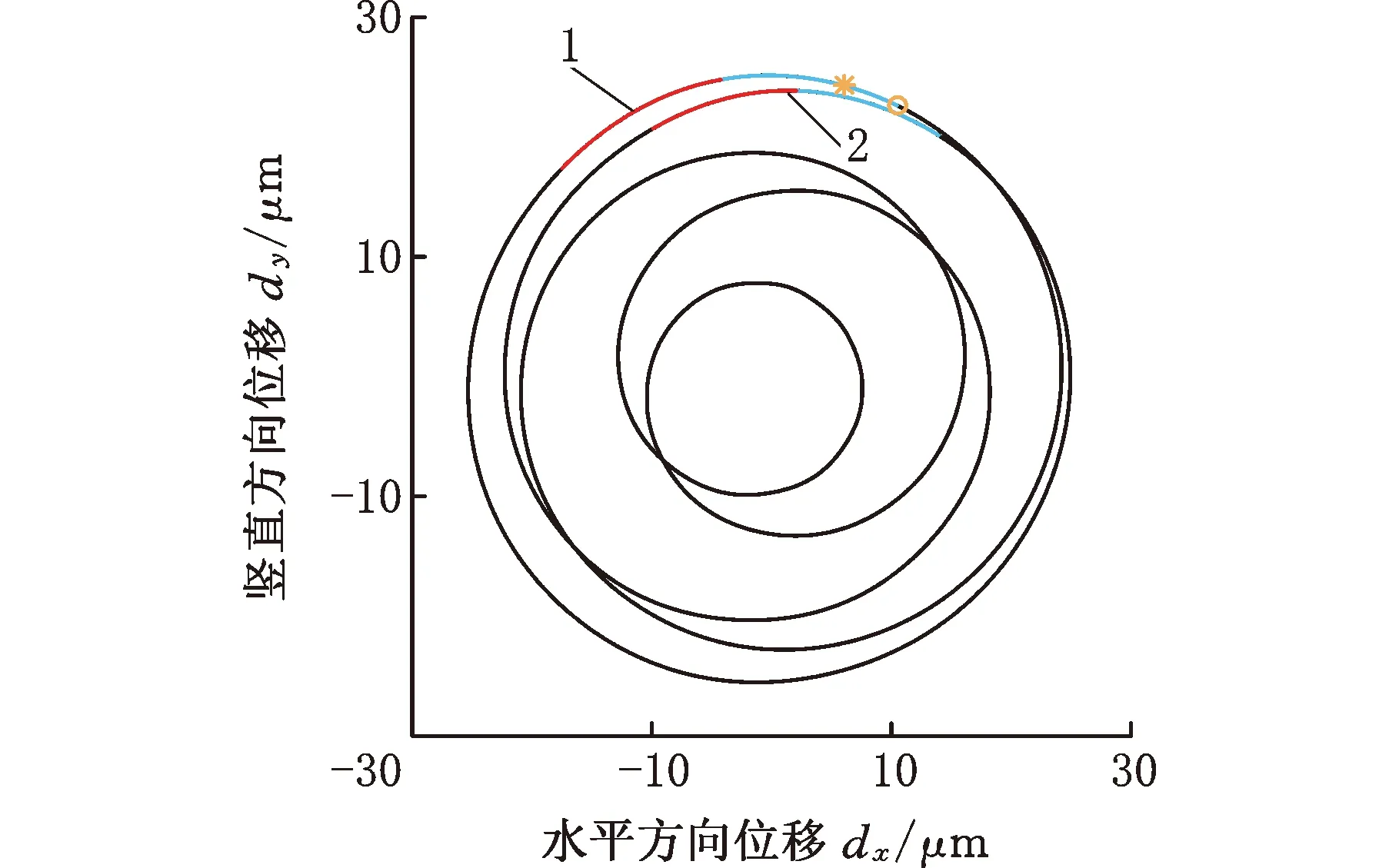
(a)內轉子

圖22 碰摩響應的頻譜圖(KP=5,KD=3×10-3,KI=0)Fig.22 Spectrogram of rubbing responses(KP=5,KD=3×10-3,KI=0)

PID控制通常先選取合適的比例系數和微分系數以保證系統具有適當的剛度和阻尼，再以減小穩態誤差、提高系統控制精度為目的來選取適當的積分系數。在實際的磁懸浮轉子系統中，過大的積分系數會使系統在低頻段的頻率特性產生滯后，在高頻段的進動模態發生失穩現象[24]。因此，本節主要分析較小積分系數對系統碰摩特性的影響。在KI=180、其他參數與3.1節示例相同的情況下，系統的碰摩響應及接觸過程如圖26～29所示，角速度對轉子響應的影響見圖30、圖31。相比于3.1節中KI=0時的碰摩響應，內轉子的渦動軌跡從圖9c的“花瓣”狀漸變為圖27a的“蝴蝶”狀，在一個運動周期內，外轉子始終處于反向渦動狀態，內轉子做反向渦動的次數從2增加到5；圖29中的接觸深度和法向沖擊力逐漸增大；圖30中，內轉子在角速度ωi=600 rad/s附近出現頻譜連續現象，轉子振幅急劇增大，系統運動開始變得不穩定；圖31a中，除了基本的周期5振動外，還在小范圍內出現了周期10振動和混沌振動。ωi=700 rad/s時，圖31b中出現5個散點，轉子仍做周期5振動。隨著積分系數的增大，在角速度不變的情況下，AMB的等效阻尼逐漸減小，在一個運動周期內，轉子做反向渦動的次數增加，各接觸過程中的接觸深度和法向沖擊力逐漸增大，轉子的頻譜成分和非線性運動更加復雜。可見，在滿足系統穩態控制精度的情況下，應選擇較小的積分系數。

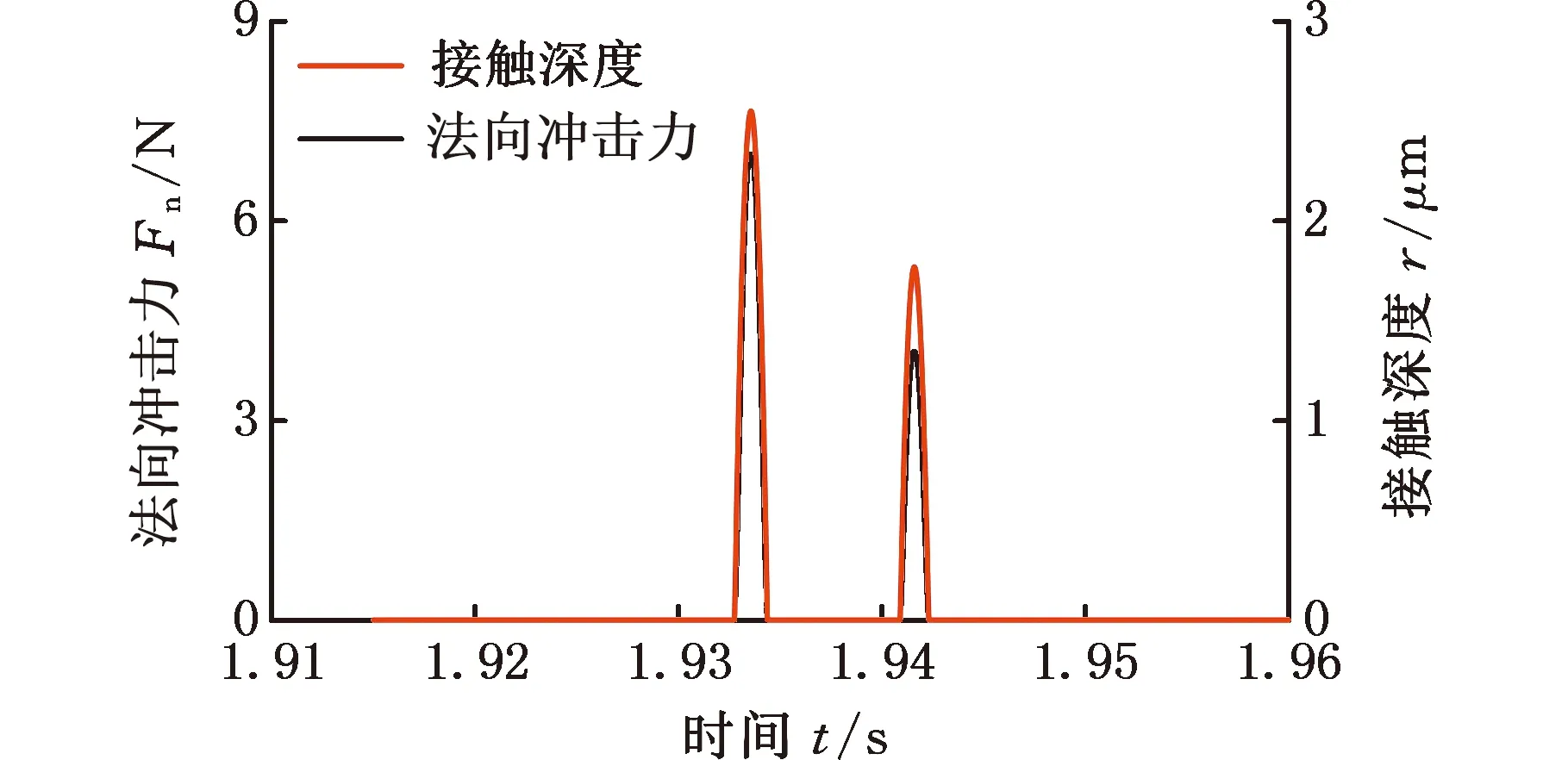
(a)法向沖擊力和接觸深度

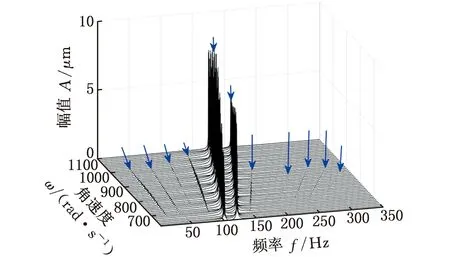
圖24 磁懸浮雙轉子系統碰摩響應瀑布圖(KP=5,KD=3×10-3,KI=0)Fig.24 Waterfall plot of rub-impact response of themagnetic suspended dual-rotor system(KP=5,KD=3×10-3,KI=0)

(a)分岔圖 (b)Poincaré圖圖25 磁懸浮雙轉子系統分岔圖與Poincaré圖(KP=5,KD=3×10-3,KI=0)Fig.25 Bifurcation diagrams and Poincaré maps ofmagnetic suspended dual-rotor system(KP=5,KD=3×10-3,KI=0)

圖26 碰摩響應的時域波形圖(KP=5,KD=5×10-4,KI=180)Fig.26 Oscillogram of time domain for rubbingresponses(KP=5,KD=5×10-4,KI=180)

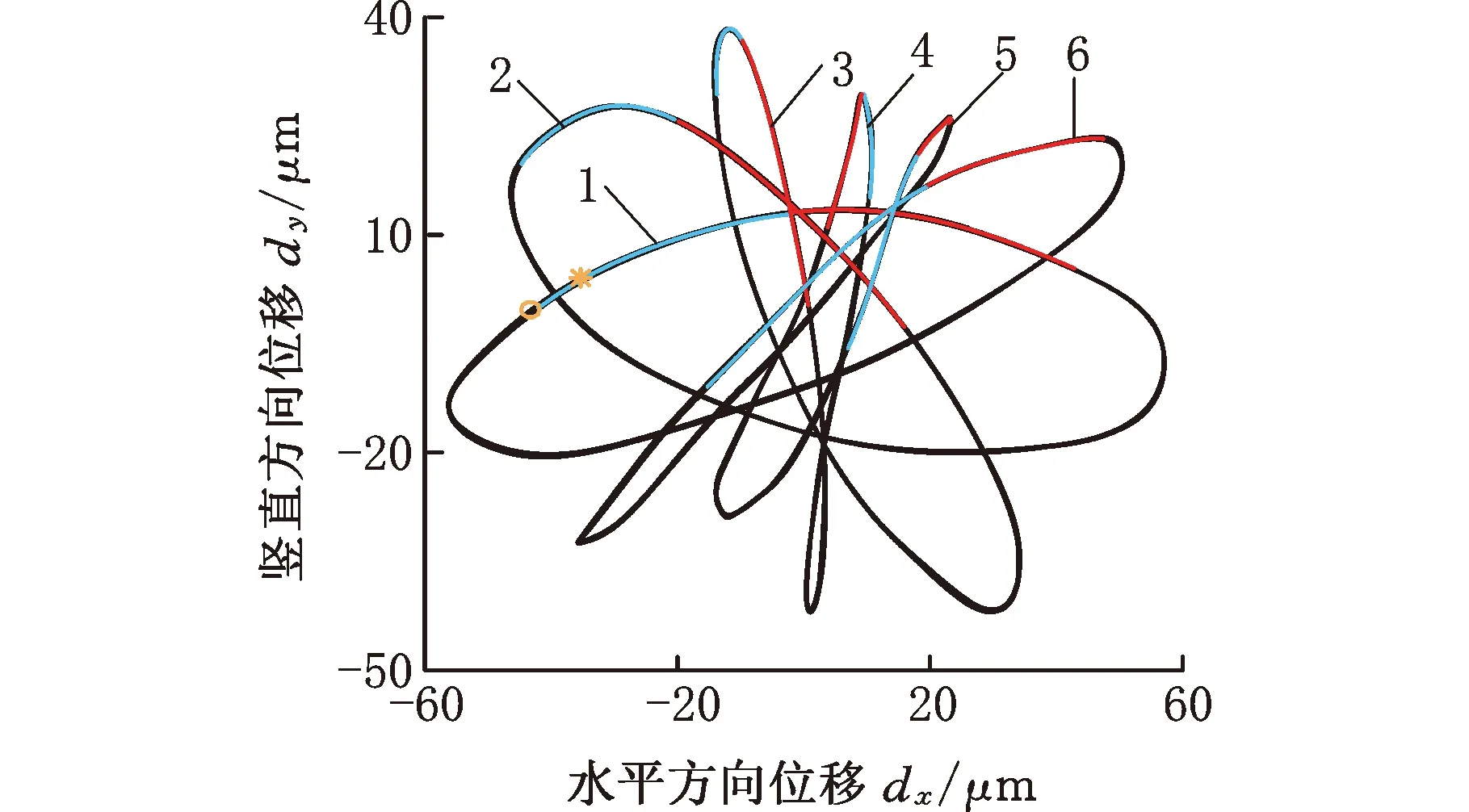
(a)內轉子

圖28 碰摩響應的頻譜圖(KP=5,KD=5×10-4,KI=180)Fig.28 Spectrogram of rubbing responsesresponses(KP=5,KD=5×10-4,KI=180)

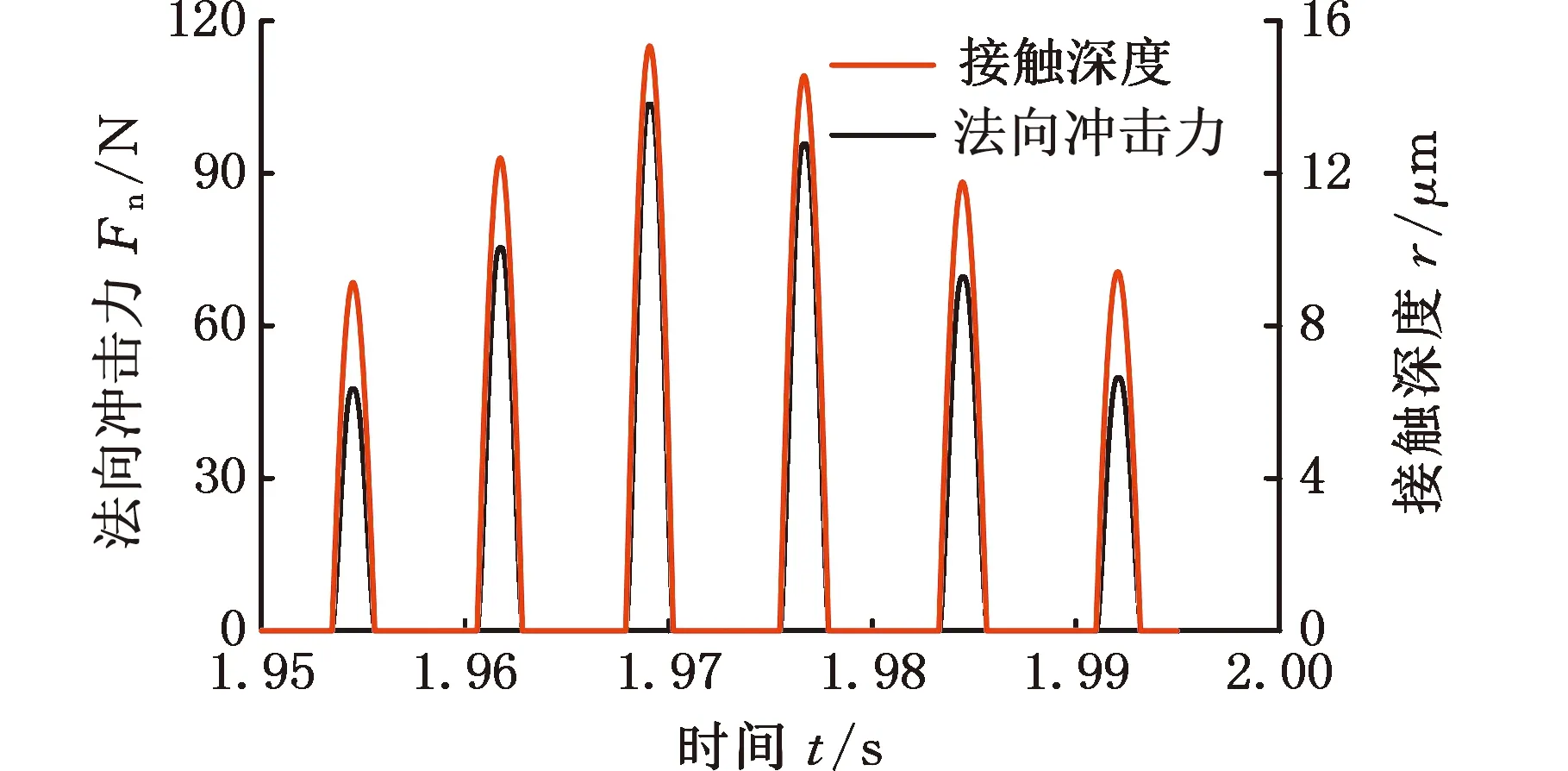
(a)法向沖擊力和接觸深度

圖30 磁懸浮雙轉子系統碰摩響應瀑布圖(KP=5,KD=5×10-4,KI=180)Fig.30 Waterfall plot of rub-impact response of themagnetic suspended dual-rotor system(KP=5,KD=5×10-4,KI=180)

(a)分岔圖 (b)Poincaré圖圖31 磁懸浮雙轉子系統分岔圖與Poincaré圖(KP=5,KD=5×10-4,KI=180)Fig.31 Bifurcation diagrams and Poincaré maps ofmagnetic suspended dual-rotor system(KP=5,KD=5×10-4,KI=180)

4 結論

(1)將不同轉速下的計算結果與文獻中的仿真結果和試驗結果進行對比，驗證了磁懸浮雙轉子系統定點碰摩故障下的動力學模型有效性。

(2)由于中介軸承的動力耦合作用，碰摩較弱時，內外轉子正向渦動，頻譜中出現整數倍的轉頻差頻率分量n(fo-fi)，其中，n=1,2,…；碰摩嚴重時，內外轉子處于反向渦動狀態，渦動軌跡復雜；隨著碰摩的進一步加劇，臨界轉速附近的頻譜不僅含有整數倍轉頻差頻率分量，還出現分數階轉頻差頻率分量n(fo-fi)/2, 其中，n=1,3,5,…。

(3)在碰摩過程的壓縮階段，轉靜部件之間的接觸深度和法向沖擊力從零增加到最大值；在分離階段，接觸深度和法向沖擊力從最大值減小為零。最大接觸深度和最大法向沖擊力取決于初始沖擊速度。

(4)比例系數和微分系數對磁懸浮雙轉子系統的定點碰摩響應有顯著影響，通過選擇使系統運行角速度遠離臨界角速度的比例系數或較大的微分系數可顯著降系統碰摩的嚴重程度。積分系數對系統的碰摩響應有一定影響，在滿足穩態控制精度下應選擇較小的積分系數。