GEO衛星對BDS相對定位性能的影響分析

祝會忠 張馨洋 楊 虎 唐龍江 李 軍

1 遼寧工程技術大學測繪與地理科學學院，遼寧省阜新市中華路47號，123000

由于GEO衛星的高軌道特性以及靜地幾何特征，其軌道的確定和預報難度較大，衛星軌道精度較低。但同時其擁有更高的區域可見性，能有效增加衛星數，進一步提高區域導航性能。研究表明，目前BDS的GEO衛星的精密定軌精度為dm級[1-5]。許多學者對GEO衛星位置計算、廣播星歷誤差、衛星鐘差、BDS服務性能以及定位精度進行了研究，然而對GEO衛星的引入對BDS高精度定位性能的改善的詳細分析較少，特別是在BDS高精度相對定位方面。因此，本文基于非差觀測模型推導BDS長距離相對定位模型，利用長距離基線估計測站位置坐標、整周模糊度和對流層延遲誤差參數；通過MGEX測站BDS觀測數據，設計BDS IGSO+MEO組合星座以及BDS全星座相對定位的靜態與動態對比實驗；同時，對GEO衛星的精密軌道精度進行研究，重點分析GEO衛星對BDS高精度長距離相對定位性能的影響。

1 BDS基本觀測模型

1.1 BDS非差觀測模型

非差偽距觀測值和載波相位觀測值是BDS最基本的觀測值，BDS相對定位采用多頻偽距和載波相位非差觀測值[6]，其觀測方程為：

(1)

(2)

式中，Φ為載波相位觀測值；P為偽距觀測值；ρ0為測站到衛星間的幾何距離；λ為載波相位波長；N為載波相位整周模糊度；下標i為頻率；I為電離層延遲誤差；T為對流層延遲誤差；ts為衛星鐘差；tR為接收機鐘差；O為衛星軌道誤差；δX為坐標初值改正量，即位置參數；H為未知參數的系數向量；上標s為衛星號；ε為觀測噪聲。

1.2 隨機模型

BDS相對定位中，多項誤差對觀測值的影響與高度角有關[7]。本文根據衛星高度角大小來確定觀測值的權重，采用基于高度角的隨機模型：

(3)

式中，σ為觀測值噪聲；a為因子；E為衛星高度角。

根據衛星高度角進行定權，其權值可表示為：

(4)

2 BDS相對定位觀測模型

2.1 由非差觀測模型確定相對定位模型

通過BDS非差觀測方程獲得相對定位模型。首先固定一個測站R為參考站，其非差載波相位觀測方程為[8]：

(5)

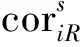
(6)

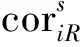
(7)

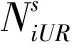
2.2 殘余誤差的處理

對于式(7)，考慮到電離層延遲誤差以及對流層延遲誤差隨基線長度的增加會存在殘余影響，因此將對流層延遲誤差用單顆衛星和測站天頂對流層延遲誤差的對流層投影函數表示。對流層投影函數可用與衛星高度角E有關的函數map表示：

(8)

天頂對流層延遲誤差參數估計可采用分段線性函數。基線兩端測站的共視衛星高度角相差很小，由于GEO和IGSO衛星的高軌道特性，基線兩端測站同一衛星的高度角相差更小，投影函數差值也較小。考慮到式(8)計算得到的2個測站的投影函數數值相近，因此對其進行合并估計。對于中長距離基線，對流層延遲誤差的殘差為：

(9)

式中，RZTD為基線兩端測站的相對天頂對流層延遲誤差參數。電離層延遲誤差殘差的處理可采用參數估計的方式進行改正，電離層延遲誤差可作為參數來估計，歷元間電離層延遲誤差參數變化可采用隨機游走過程進行約束。

3 實驗與結果分析

采用香港、澳大利亞地區MGEX測站中的3組基線觀測數據，觀測時間為2018年doy050～075，詳細情況見表1。分別以STR1、HKWS、PERT站為基準站，對3組實驗數據進行靜態和動態BDS高精度相對定位實驗，測站位置以及GEO衛星分布見圖1。以GFZ精密星歷產品為參考驗證BDS衛星精密軌道精度，以SLR數據作為參考值，根據GEO/IGSO/MEO衛星軌道的徑向誤差進行分析。選取GEO衛星C01、IGSO衛星C08和C10、MEO衛星C11進行統計分析，4顆衛星徑向誤差的STD和RMS值見表2。

表1 實驗數據

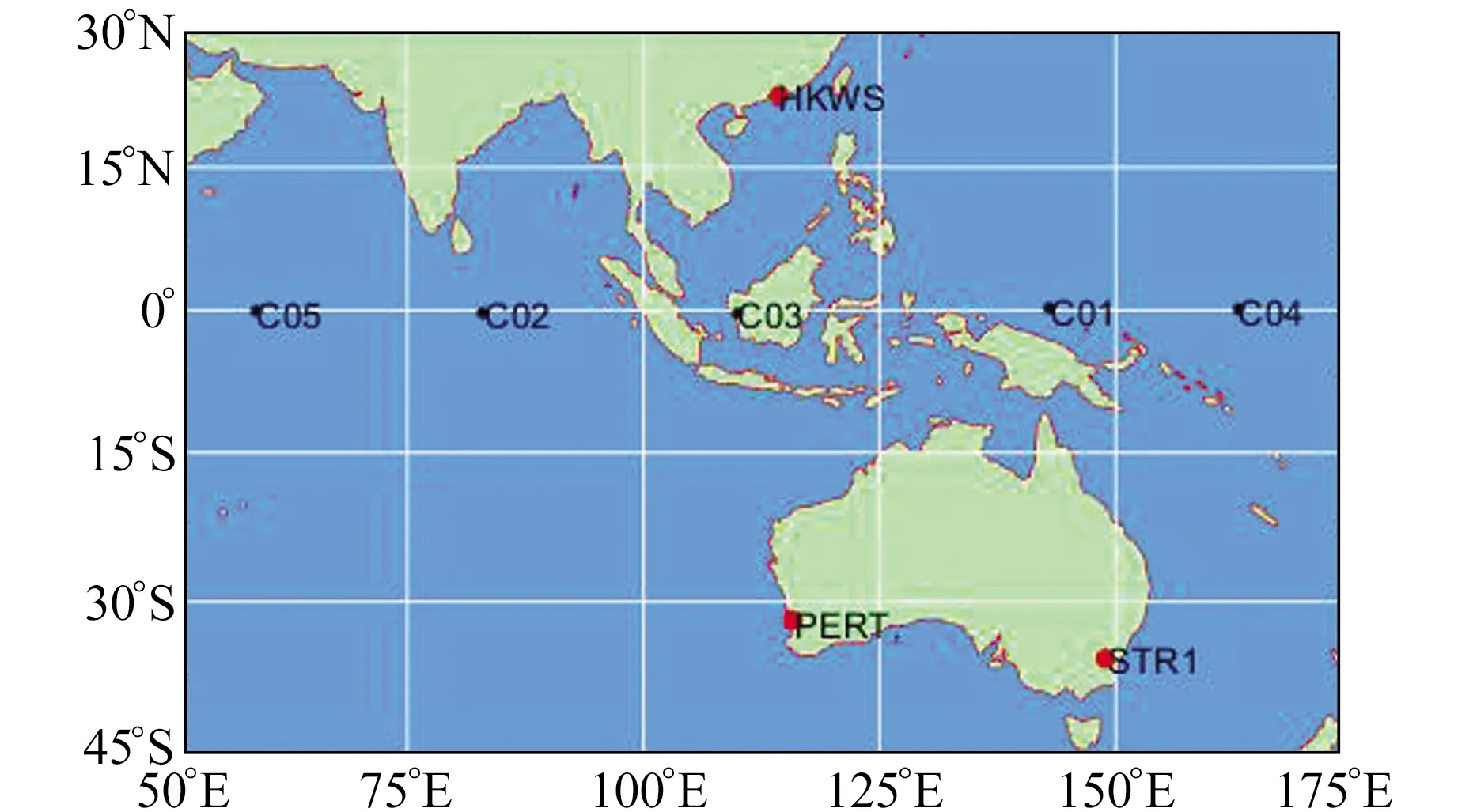
圖1 測站分布

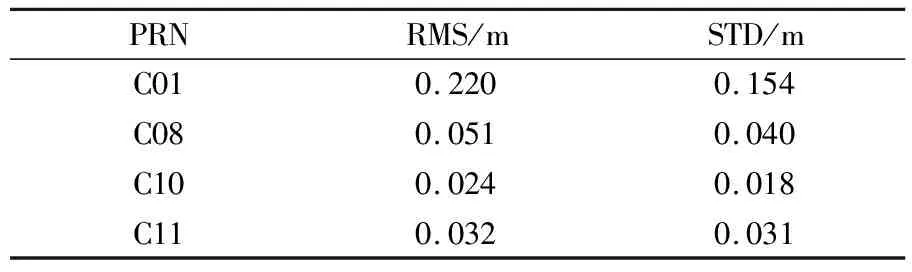
表2 徑向誤差的RMS和STD比較

由表2可知，GEO衛星軌道精度明顯低于IGSO和MEO衛星。但GEO衛星在特定地區可被長期穩定地觀測到，能夠增加BDS衛星星座的可用衛星數量，改善衛星觀測條件，增強觀測模型的幾何構型。在數據解算過程中，可通過采用降低GEO衛星觀測值權重的方法降低GEO衛星的影響。

3.1 靜態相對定位結果分析

利用不同地區3條基線的觀測數據分析GEO衛星對BDS靜態相對定位的影響，以IGS周解的測站坐標作為參考值，采用2種BDS靜態相對定位實驗方案：方案1采用IGSO+MEO組合，方案2采用IGSO+MEO+GEO全星座組合。3組測站在各觀測時段均包含3顆以上GEO衛星的觀測數據。

以doy056為例分析3個基準站可見衛星數和PDOP值，結果見圖2。可以看出，加入GEO衛星后，在衛星數較少時，GEO衛星能夠顯著改善幾何構型，對加快解算收斂速度和提高定位精度有提升作用。

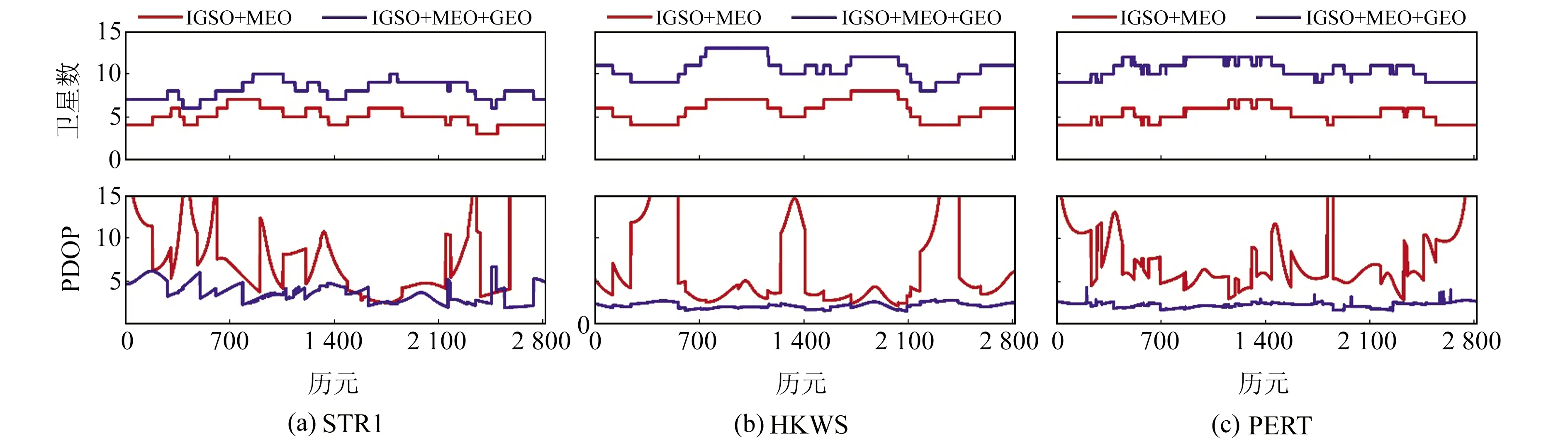
圖2 可見衛星數量和PDOP值

圖3為方案1和方案2靜態相對定位單天解，定位結果統計信息見表3。

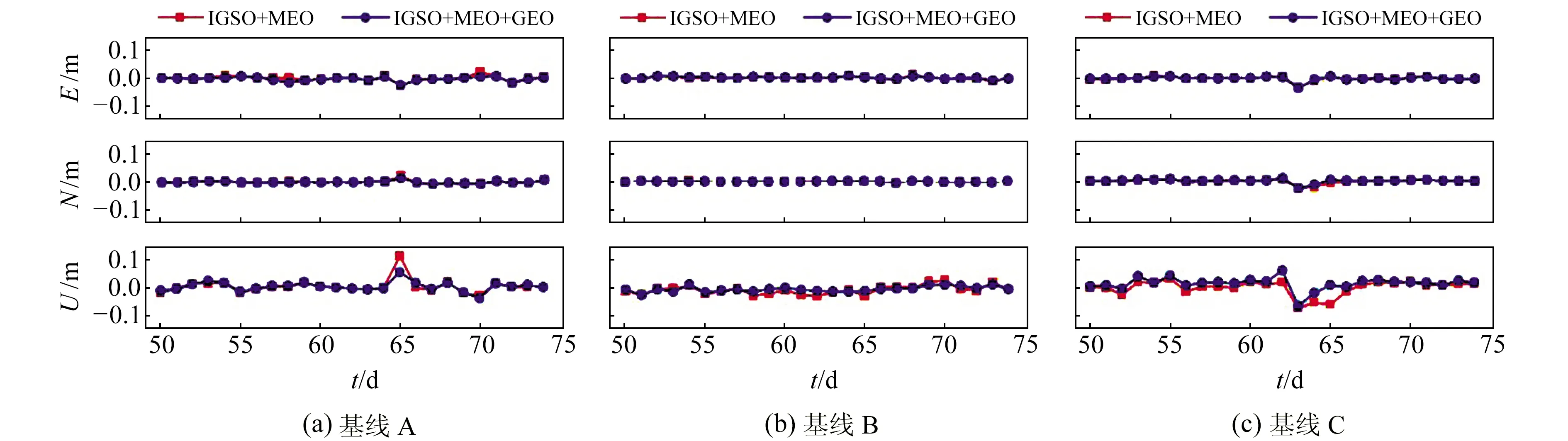
圖3 靜態基線單天解偏差

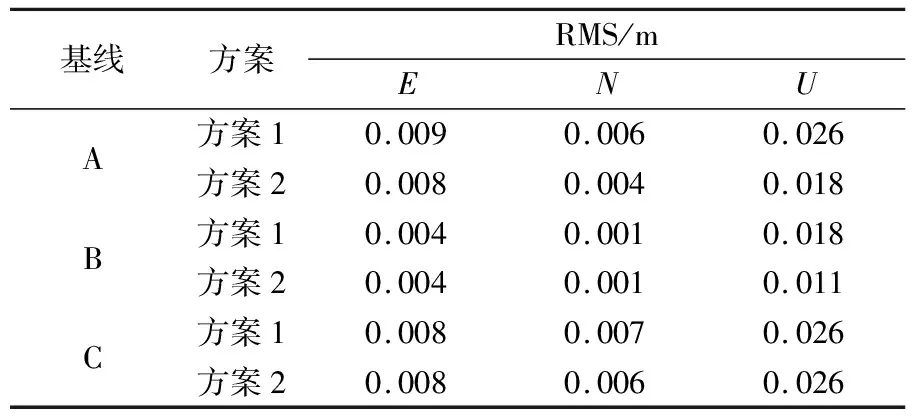
表3 靜態基線精度統計

可以看出，方案2各方向靜態基線單天解精度均優于方案1。2種方案各測站平面精度均優于0.01 m，達到mm級；U方向上，2種方案均優于0.03 m。但因為單天24 h的觀測數據時間較長，不使用GEO衛星的MEO+IGSO組合的定位精度相對于全星座差別較小。

將24 h分為12個觀測時段，每段2 h，以doy056為例進行靜態基線解算，定位結果見圖4，統計結果見表4。

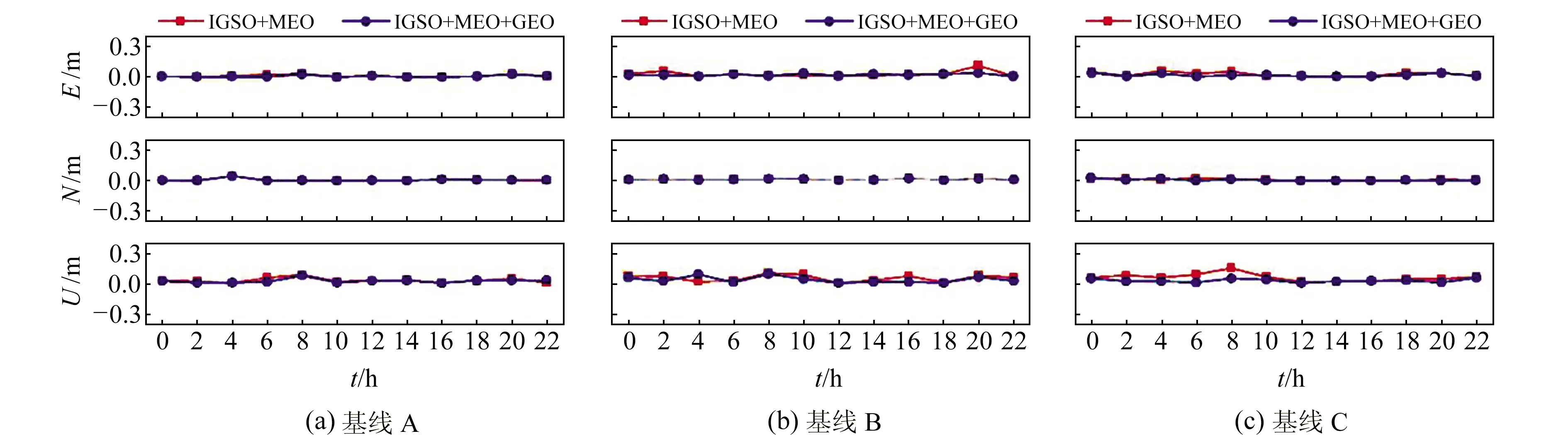
圖4 2 h靜態基線誤差對比

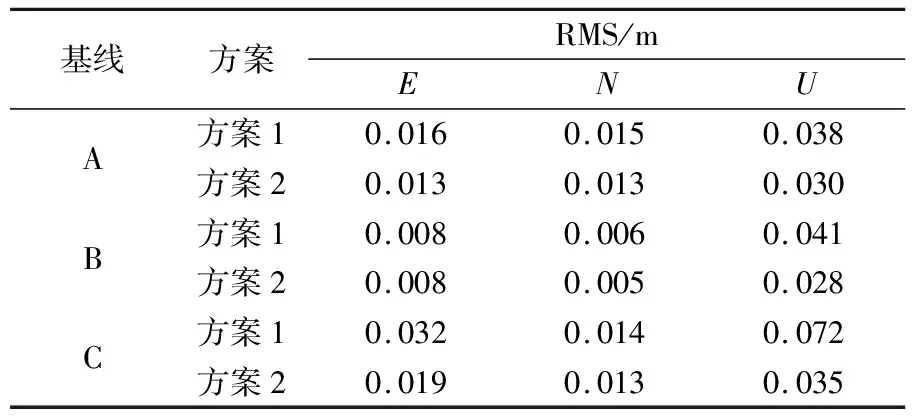
表4 2 h靜態基線精度統計

可以看出，加入GEO衛星對靜態相對單天解和2 h解中U方向精度提升最為明顯，E、N方向也有不同幅度提升。觀測時長越短，GEO衛星對靜態相對定位性能的提升越顯著。相對定位模型對衛星軌道誤差具有一定削弱作用，因此GEO衛星的軌道精度對相對定位，特別是中短基線的影響較小。

3.2 動態相對定位結果分析

為了更準確地對模擬實時動態基線解算結果的收斂時間進行分析，以實時動態方式處理3條基線doy056的數據，定位結果見圖5(圖中neq為法方程協因數主對角線上3個元素的矢量和)。可以看出，2種組合的法方程差異較大，加入GEO衛星后能有效改善衛星幾何構型，提高定位精度。以doy056為例，對動態相對定位收斂后精度進行統計，統計結果見表5。

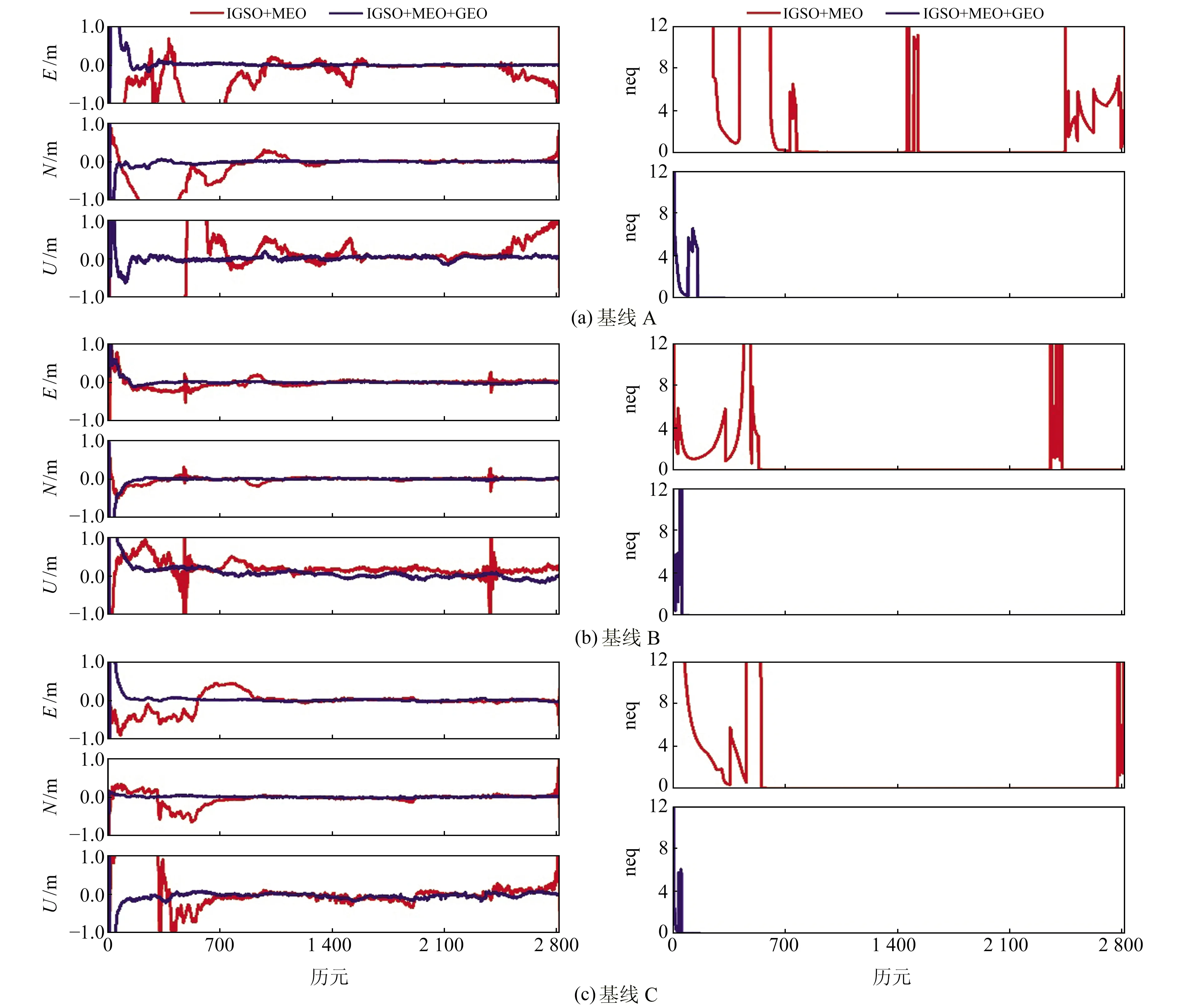
圖5 動態基線誤差比較

從圖5和表5可以看出，加入GEO衛星后，3條基線動態解算結果均有大幅提升。圖6為doy056第1時段BDS動態相對定位偏差。對3個方向的誤差進行RMS統計得到收斂時間，統計結果見表6(單位min)。從表中可以看出，GEO衛星能顯著提升BDS實時動態相對定位的定位性能，其中基線C在方案1動態模式下不收斂，方案2中，3個方向在60 min左右就可收斂到0.1 m以內，動態相對定位的結果和收斂速度大幅提升。

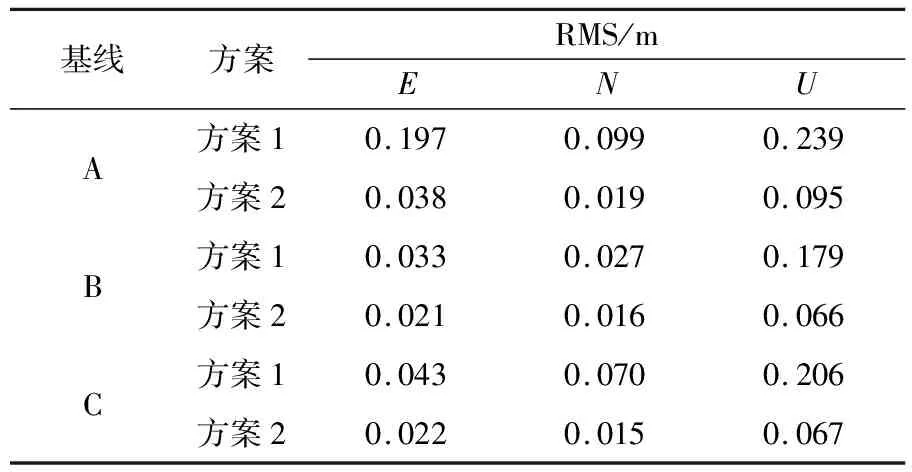
表5 動態相對定位精度統計

表6 收斂時間統計

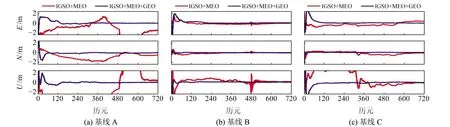
圖6 第1時段BDS動態相對定位偏差

4 結 語

基于高精度相對定位方法，利用靜態和動態2種數據處理模式對包含GEO衛星的BDS全星座模式和不包含GEO衛星數據處理模式的2種實驗方案的定位精度、PDOP值、收斂速度以及法方程等方面進行性能分析。結果表明，BDS全星座的衛星個數較多，各測站定位結果、PDOP值和幾何構型均較為穩定；不包含GEO衛星的數據處理中，觀測時長較短或動態定位時，定位結果以及PDOP值起伏較大，平面精度優于U方向，N方向精度最高。靜態相對定位單天解和2 h解中，缺失GEO衛星的定位精度低于全星座，其中2 h解算結果更為明顯。缺少GEO衛星的動態定位相對于全星座的定位性能降低明顯。雖然GEO衛星的軌道徑向誤差相對于IGSO和MEO衛星較大，但衛星數量和觀測值的增加可明顯提升定位性能，特別是衛星數較少的時段和動態定位數據處理模式，在較短的觀測時間內可顯著提升定位效果。而且相對定位中，通過差分組合降低了衛星軌道誤差的影響，GEO衛星軌道徑向誤差大的缺陷可以通過相對定位的方式克服。