基于滑動奇異譜分析方法的重力固體潮提取

王建波 王晉南 孫 潔 齊鑫敏 劉相威 高文宗

1 江蘇海洋大學海洋技術與測繪學院，江蘇省連云港市蒼梧路59號，222005 2 菏澤市測繪研究院，山東省菏澤市珠江路1717號，274002 3 山東科技大學測繪與空間信息學院，青島市前灣港路579號，266590

雖然CG-5重力儀自帶軟件可提供固體潮改正值，但理論模型是建立在理想條件和固定參數的基礎上的，其計算得到的重力固體潮理論值與實際值之間存在一定差異。如何快速從相對重力觀測數據中分離重力固體潮改正，對相對重力觀測具有重要意義。

SSA方法可以對原先一維時間序列時延排序得到的時滯矩陣進行分解和重構，提取出原序列中代表不同成分的信號，如周期信號、趨勢信號、噪聲信號等。郭金運等[1]采用該方法提取重力固體潮，并進行周期為10 d的靜態相對重力固體潮提取實驗，取得很好的效果。雖然相對重力儀靜態零漂線性度很好，但零漂總體呈下降趨勢[2]。另外，相對重力儀在長時間靜態重力觀測時會受到觀測時間長、零漂線性度改變、非線性誤差[3]以及復雜環境噪聲的影響，這些影響因素會降低SSA方法提取重力固體潮的精度。為此，本文提出滑動SSA方法，通過設置奇異譜分析數據長度時間窗口，解決長時間靜態相對重力觀測時重力固體潮的提取問題。

1 原理與方法

1.1 SSA方法、重力固體潮粗差識別及修復

SSA方法的原理、粗差識別及迭代插值方法可參見文獻[1]。用SSA方法提取重力固體潮時，一般先利用ω-correlation方法[4]對重建成分(RCs)進行頻譜分析和重構。而本文理論重力固體潮值選取與之不同，分為2種：1)對實測重力數據采用Eterna調和分析獲得潮波參數，然后用TSoft軟件[5]計算得到理論重力固體潮值；2)用CG-5重力儀自帶軟件進行計算。

粗差識別時，利用SSA方法獲得原靜態相對重力觀測時間序列的主成分，計算原靜態相對重力觀測時間序列與主成分之間的殘差，分析殘差值時間序列，并以3σ閾值原則識別粗差。具體過程為：利用SSA方法處理原靜態相對重力觀測時間序列，利用ω-correlation方法分析各重建成分之間的相關性，找出趨勢項、周期項以及第i階次，當重建成分階次大于i時，各個重建成分之間不能很好地分離；合并前i階項得到主成分，計算原相對靜態重力觀測值序列和主成分序列之間的殘差并識別粗差。

本文通過奇異譜迭代方法插補粗差處的重力值，與文獻[1]不同之處在于：將殘差時間序列中粗差位置處的殘差值設置為0，然后通過SSA方法分解重構重建殘差趨勢項，用趨勢項的值代替原缺失位置的0值。循環此過程，直至缺失位置處前后兩次插補的數據殘差RMS小于10-3μGal。這時，將重建的殘差數據序列與之前提取的主成分數據序列相疊加，得到修正后的靜態相對重力時間觀測序列。

1.2 零漂和固體潮提取思路

針對長時間靜態相對重力觀測數據中零漂和固體潮的變化特點和SSA方法分析有限長度周期性信號的特點，本文提出采用滑動SSA方法提取長時間重力固體潮改正：

1)將原M天的靜態相對重力觀測值時間序列按L天為一個時間段進行滑動分組，滑動窗口長度為1 d，即任意相鄰兩組數據序列的起始時間相隔1 d，得到每個時間段M-L+1組數據序列。

2)對每個時間段內每組靜態相對重力觀測值序列，利用多項式擬合得到L天內的零漂值。從每組觀測值中減去對應多項式擬合計算得到的零漂值，對其結果采用SSA方法提取固體潮，然后提取每組數據序列的固體潮改正。

3)對每個時間段內M-L+1組數據均通過多項式擬合提取零漂，將剔除零漂后的重力數據觀測序列通過SSA方法提取重力固體潮改正值。重力固體潮(或零漂)按同一天取平均值獲得當天重力固體潮改正(或零漂)的最終結果，即第1～M天分別在第1、2、…M-L+1組中找到對應值，并按1 d、2 d、…、M天取平均。為降低SSA中邊界效應的影響，在精度對比統計中不統計每組前2 d和最后2 d的數據。

2 實驗與分析

2.1 實驗數據及數據預處理

相對靜態重力觀測時間序列中除包含重力固體潮外，還包括海潮負荷、零漂和噪聲等。本次實驗利用CG-5相對重力儀(序列號41221)在固定點(坐標120.10°E、36.00°N；大地高25.5 m)進行連續2個月(2016-03-05 00：00～05-04 23：59)的靜態相對重力觀測。相對重力儀采樣頻率為6 Hz，儀器前55 s進行數據采集，后5 s進行數據處理，因此1 min內可得到330個數據。相對重力儀自帶地震濾波功能，可對獲取的靜態相對重力觀測數據進行低頻噪聲過濾，舍棄高于6倍標準偏差的高頻噪聲。濾波之后對樣本數據每分鐘進行一次平均處理并且作為結果自動記錄，61 d共獲得87 840個數據。對相對重力觀測數據進行預處理，采用本文提出的方法進行重力固體潮改正提取。作為對比，采用多項式擬合提取零漂，將剔除零漂后的重力數據采用SSA提取重力固體潮改正，技術路線如圖1所示。

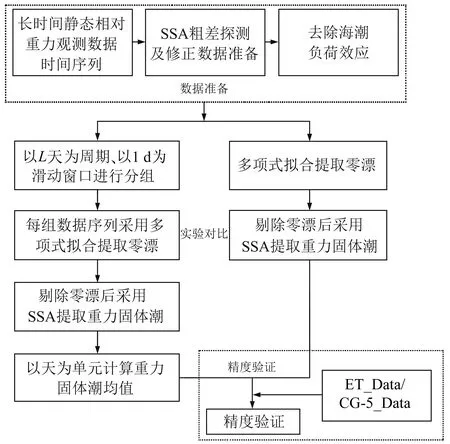
圖1 滑動SSA提取重力固體潮技術路線

首先利用SSA方法進行粗差探測，將4 d共5 760個重力觀測數據作為嵌入維數，對87 840個相對重力觀測數據時間序列進行SSA分解和重構，獲得RCs；通過ω-correlation方法分析各RC之間的相關系數，前30階重構成分ω-correlation分析結果如圖2所示。根據相鄰兩個RC之間的相關系數大于0.85可以判斷，R2、R3、R4、R5、R7、R8、R9、R10、R16、R17、R20、R21、R26、R27、R28、R29均具有周期性。從重力數據序列SSA得到的前30階重構部分FFT功率譜分析結果(圖3)可以看出，從第15階開始，不同頻率混疊較嚴重，而且振幅非常小，各重構成分之間無法很好地分離，因此合并前14項重構成分作為原重力數據時間序列主成分。原靜態相對重力觀測與主成分之間殘差時間序列如圖4(a)所示，根據3σ準則選擇閾值區間為(-0.009 8 mGal，0.009 8 mGal)，若超出此閾值區間則判定為粗差，共624個。根據奇異譜迭代方法修正殘差處的粗差相對重力值，經過迭代后得到粗差處相鄰兩次迭代修復值殘差的RMS為9.57×10-6μGal，修復后的殘差值如圖4(b)所示。可以看出，殘差序列較為平穩，插補效果良好。修復后的殘差疊加主成分可得到修復后的靜態相對重力觀測時間序列，結果如圖5(a)所示。海潮和重力固體潮成因相同，因此具有相同的頻率。本文基于NAO.99b海潮模型[6]，結合TSoft軟件計算本次實驗同歷元下的重力海潮負荷值時間序列，結果如圖5(b)所示，將海潮對相對重力的影響從原時間序列中去除，結果如圖5(c)所示。

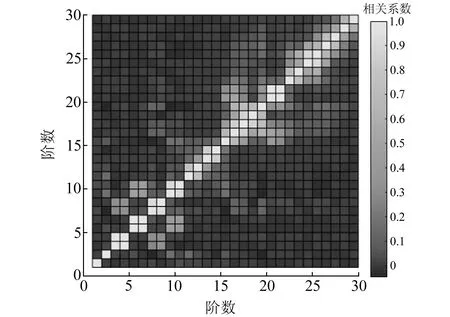
圖2 靜態相對重力數據序列SSA前30階重建部分的ω-correlations

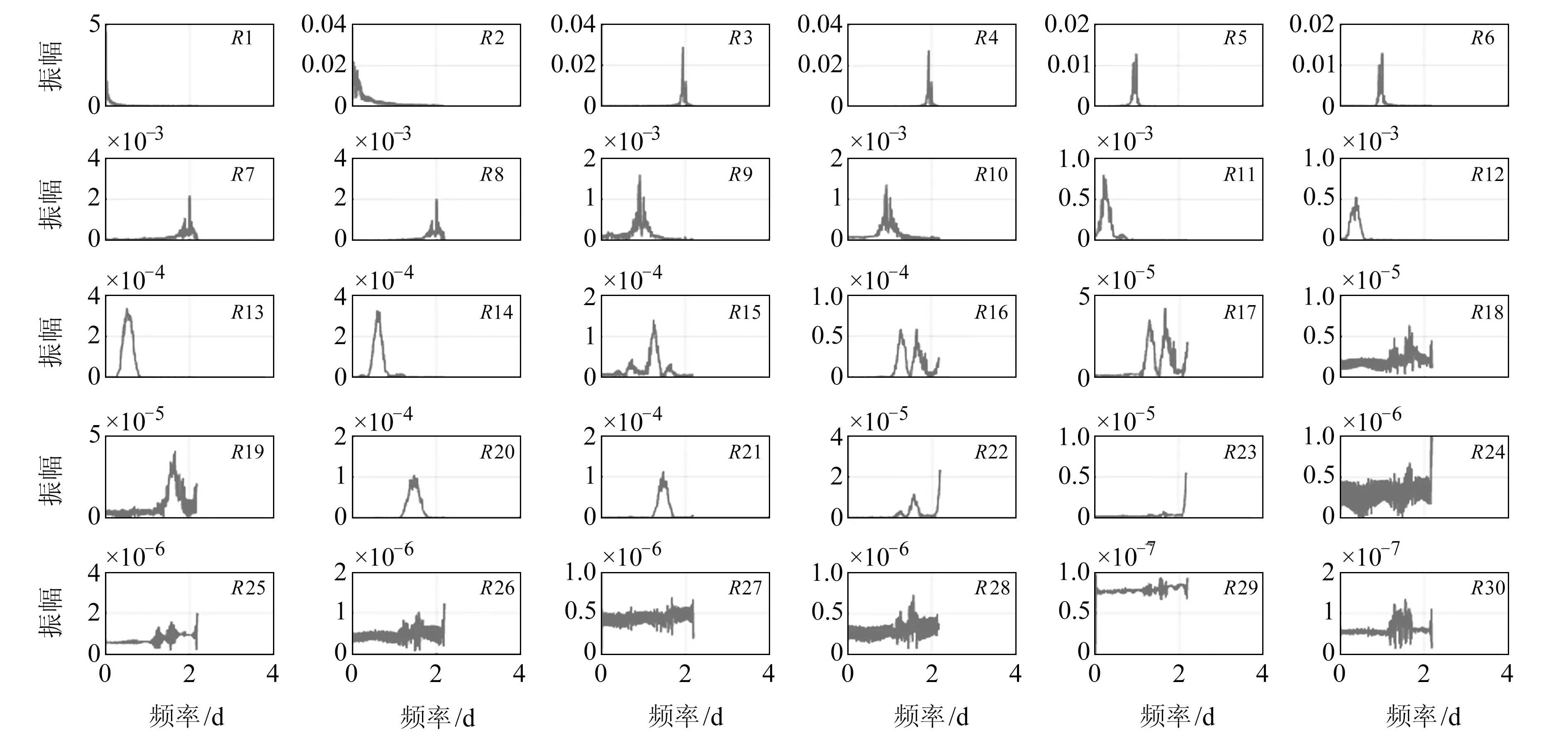
圖3 靜態相對重力數據序列SSA前30階重構部分的FFT功率波譜分析

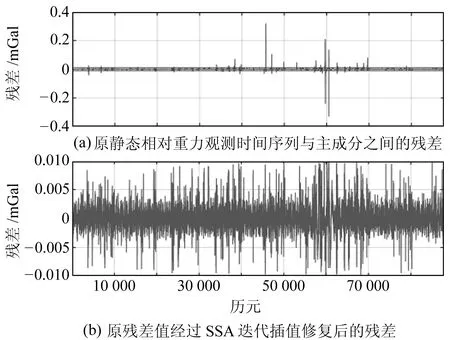
圖4 原靜態相對重力觀測時間序列與主成分之間的殘差

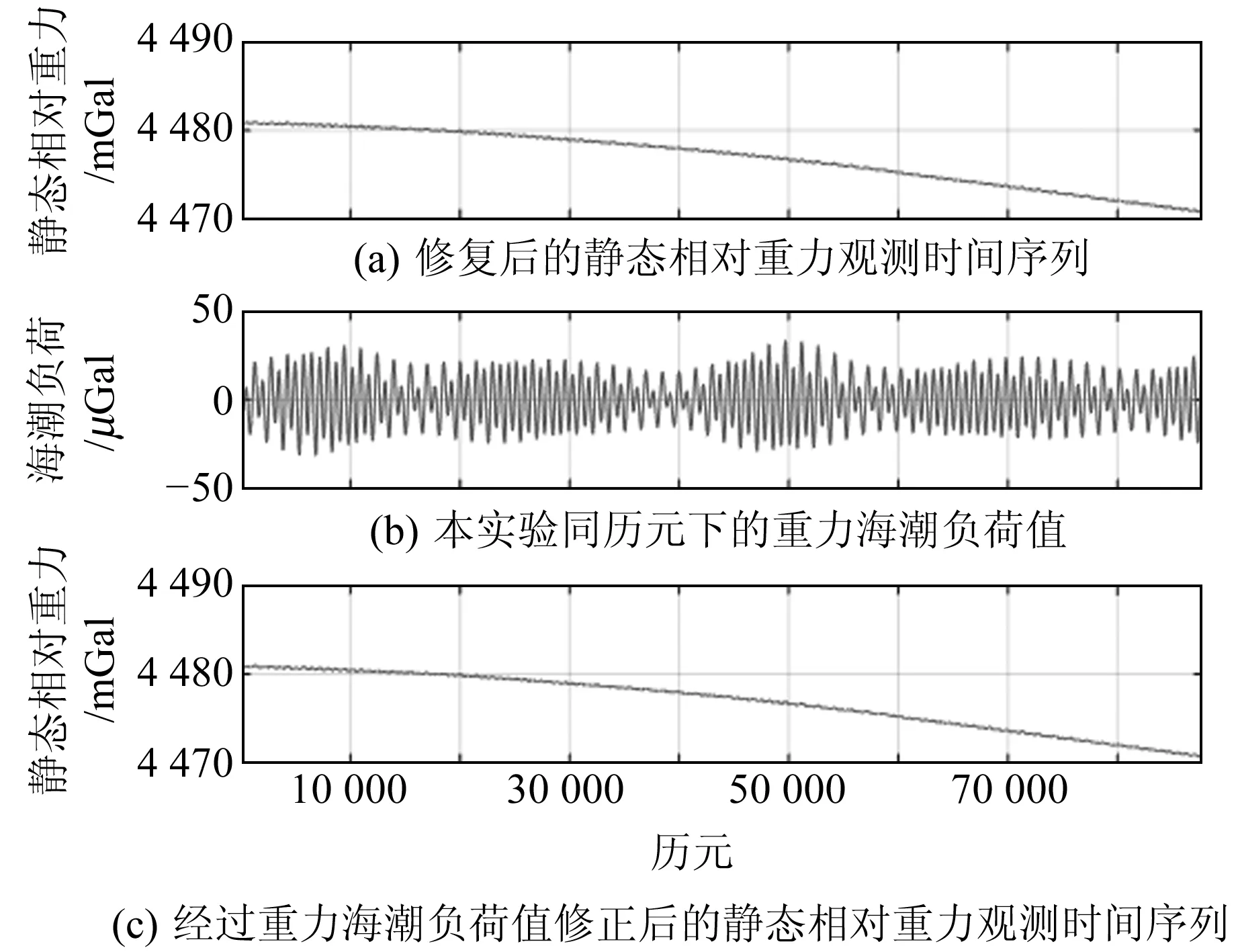
圖5 靜態相對重力觀測時間序列

2.2 滑動SSA方法提取重力固體潮改正

為了驗證滑動SSA方法提取重力固體潮改正的效果，對61 d靜態相對重力觀測時間序列分別以10 d、15 d、20 d、25 d、30 d、40 d、50 d為時間段，并以1 d為滑動窗口進行分組，得到每個時間段內包含的數據序列組數分別為52、47、42、37、32、22和12。

在提取重力固體潮之前，首先需要剔除每組靜態相對重力觀測數據中的零漂項。采用SSA方法識別CG-5相對重力觀測數據中的趨勢，將SSA窗口長度設為4 d，對每組數據進行分解和重構，得到趨勢項RC1。然后采用多項式擬合提取零點漂移，擬合公式為：

y=ax2+bx+c

(1)

式中，a、b、c為擬合參數。利用SSA提取零漂時可剔除噪聲，因此效果會更好。對每組數據序列剔除擬合后的零漂值，然后選擇嵌入維數5 760進行 SSA，對重構成分進行ω-correlation相關性分析。個別分組中兩個相鄰RC之間的相關系數大于0.80時無數據，因此對比實驗中均選擇相關系數大于0.65(當相關系數為0.75時結果類似，相關系數為0.65時提取結果精度提高更明顯)。從重構項i≤15中得到每組中同頻率重構序列，對重構序列進行合并。對每組重構序列進行求和，計算每組提取的重力固體潮改正。SSA在分解重構過程中存在邊界效應，因邊界效應不是本文主要研究內容，為削弱其影響，將每組前2 d和最后2 d共5 760個重力固體潮提取結果舍去，再采用本文方法計算最終的重力固體潮改正值，得到的結果分別記為HSSA_10、HSSA_15、HSSA_20、HSSA_25、HSSA_30、HSSA_40和HSSA_50。

為了驗證提取精度，將實測重力數據采用Eterna調和分析獲得潮波參數后用TSoft軟件計算得到重力固體潮值(記為ET_Data)和CG-5重力儀自帶軟件計算的重力固體潮值(記為CG5_Data)分別作為參考值，提取結果與同時刻ET_Data和CGS_Data之間的差值如圖6所示，差值統計如表1(單位μGal)所示。

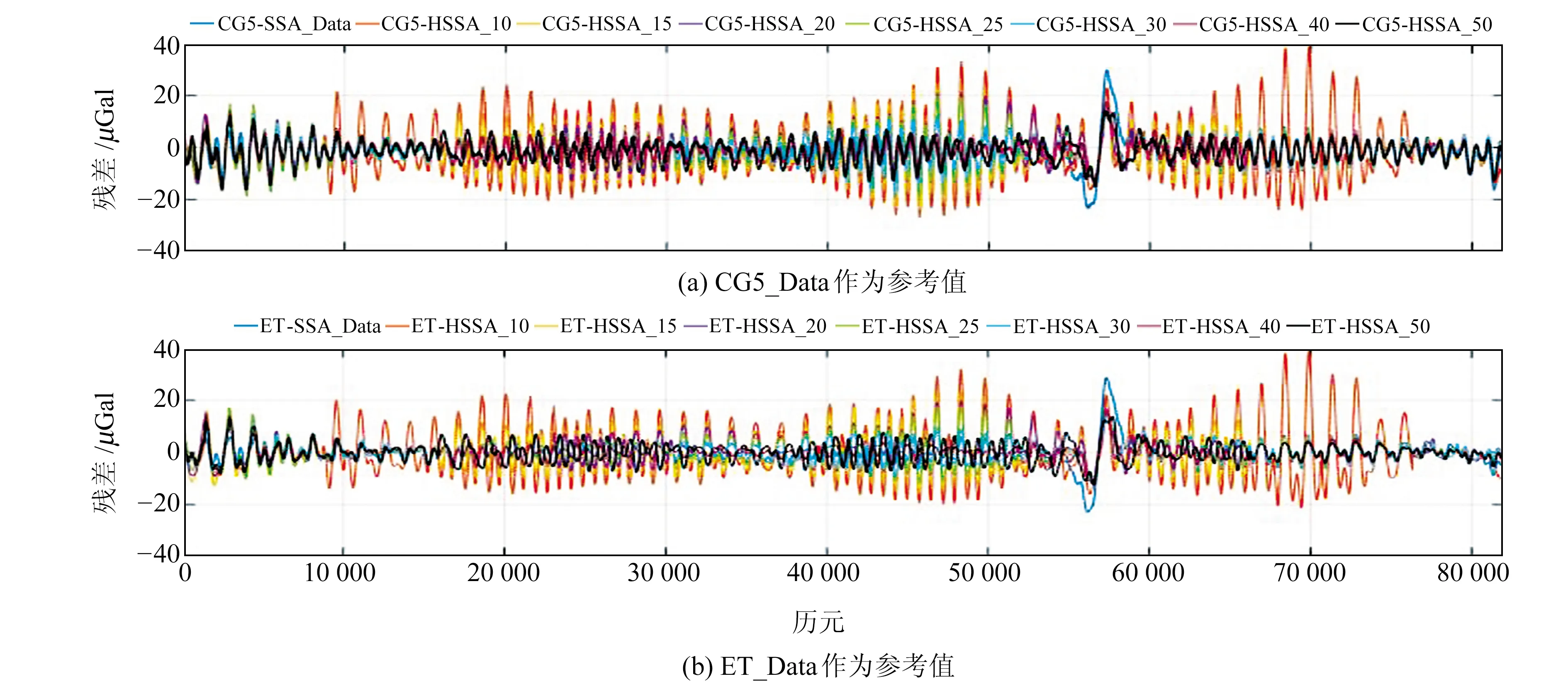
圖6 不同方法提取的重力固體潮殘差對比

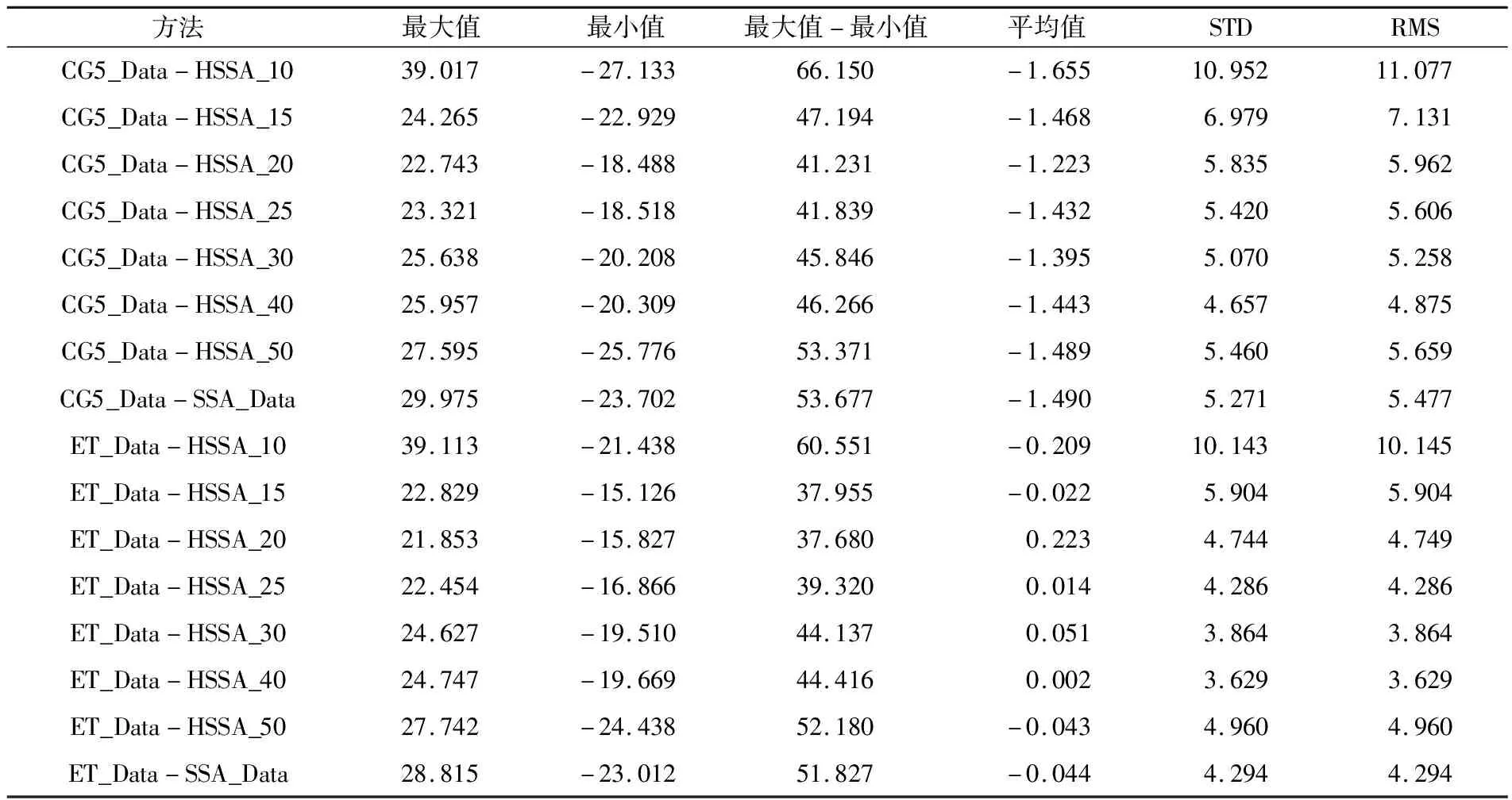
表1 滑動SSA和SSA提取長時間重力固體潮殘差統計

2.3 多項式擬合方法提取零漂和SSA提取重力固體潮

將61 d靜態相對重力觀測數據序列作為一個時間段長度，采用多項式擬合方法提取零漂值，設嵌入維數為5 760，利用SSA分解重構獲得RC1趨勢項，并利用式(1)進行多項式擬合。將零漂數據從靜態相對重力序列中剔除，然后選擇嵌入維數5 760進行SSA，對重構成分進行ω-correlation相關性分析，從結果中選出重構項i≤15和相關系數大于0.65的兩個相鄰RC項，得到同頻率重構序列，并對重構序列進行合并。對重構序列進行求和，計算提取的重力固體潮改正，得到的結果記為SSA_Data。為削弱邊界效應影響，同樣將前2 d和最后2 d共5 760個重力固體潮提取結果舍去，其與同時刻ET_Data和CG5_Data的結果比較如圖6所示，差值統計如表1所示。

2.4 不同方法提取重力固體潮殘差分析

由表1可知，無論是滑動SSA還是SSA方法，提取重力潮改正結果與理論值差值的標準差(STD)均小于11 μGal，說明SSA方法提取重力固體潮改正結果較可靠，精度較高。對于同一種提取重力固體潮改正方法，選用CG5_Data作為理論參考值，其提取結果比選用ET_Data作為理論參考值時大，說明SSA或滑動SSA方法的提取結果更接近ET_Data理論值。采用滑動SSA提取重力固體潮改正時，每個連續時間段長度不同，其提取結果與理論值殘差的STD和RMS不同。選擇連續時間段長度為30 d和40 d時，滑動SSA提取重力固體潮改正值與理論值殘差的STD和RMS比SSA方法更小，結果更優。選擇滑動時間段長度為10 d、15 d、20 d、25 d和50 d時，滑動SSA方法提取重力固體潮改正值與理論值殘差的STD和RMS大于SSA方法，表明SSA方法更優。選擇滑動時間段長度為30 d時，滑動SSA方法提取重力固體潮改正值與ET_Data理論值殘差的STD和RMS比SSA方法均小0.43 μGal；滑動SSA方法提取值與CG5_Data理論值殘差的STD和RMS比SSA方法分別小0.201 μGal和0.219 μGal。選擇滑動時間段長度為40 d時，滑動SSA方法提取重力固體潮改正值與ET_Data理論值殘差的STD和RMS比SSA方法均小0.665 μGal；滑動SSA方法提取值與CG5_Data理論值殘差的STD和RMS比SSA方法分別小0.614 μGal和0.602 μGal。選擇滑動時間段長度為10 d時，采用滑動SSA方法提取重力固體潮時，提取結果與理論值差值的STD和RMS最大，即提取精度最低。殘差最大值與最小值之間的差值可表明殘差范圍，范圍越小說明殘差的離散程度越小。當選用CG5_Data作為理論參考值時，除選擇10 d進行滑動計算的結果外，滑動SSA方法提取結果的離散程度均小于SSA方法，提取結果殘差離散程度最小的方法為選擇20 d進行滑動計算；當選用ET_Data作為理論參考值時，除選擇10 d、50 d滑動計算外，滑動SSA方法提取結果的離散程度均小于SSA方法，提取結果殘差離散程度最小的方法為選擇20 d進行滑動計算。結果表明，通過滑動SSA方法提取固體潮可降低提取結果殘差的離散程度。

由圖6可知，殘差序列均在零值附近擺動，說明提取的零漂與參考信號擬合程度較高。殘差時間序列仍然具有明顯的周期性，因為相對重力序列中除零漂和固體潮外，還包括其他因素產生的周期信號，如天氣變化、水文變化以及其他干擾噪聲，這些因素在殘差序列中會有所反映。由于ET_Data理論值是實測重力數據采用Eterna調和分析獲得潮波參數，再利用TSoft軟件計算得到的，以ET_Data為參考值時比以CG5_Data為參考值時殘差振幅略小。選用不同連續時間段進行滑動計算的結果區別較大，其中選用連續時間段30 d、40 d計算結果較好。

3 結 語

本文將時間長度為2個月的靜態相對重力觀測數據序列按時間窗口10 d、15 d、20 d、25 d、30 d、40 d和50 d分別分為52組、47組、42組、37組、32組、22組和12組，采用滑動SSA方法進行重力固體潮改正提取實驗。結果表明，SSA方法提取重力固體潮結果精度較高，采用滑動SSA和SSA方法提取的重力固體潮值與理論值(CG5_Data和ET_Data)殘差的標準差均小于11 μGal。與SSA方法相比，選用合適時間段長度的滑動SSA方法提取固體潮可以降低提取結果殘差的離散程度。選用CG5_Data值作為參考值、連續30 d和40 d數據作為一組時，滑動SSA方法提取的重力固體潮改正結果殘差的RMS比未使用滑動SSA方法時分別小0.219 μGal和0.602 μGal；選用ET _Data值作為參考值、連續30 d和40 d數據作為一組時，滑動SSA方法提取的重力固體潮結果殘差的RMS比未使用滑動SSA時分別小0.430 μGal和0.665 μGal。因此，選擇合適的連續滑動時間段，滑動SSA方法比SSA方法提取重力固體潮改正結果精度略高。