基于相關函數的錨桿智能檢測方法

袁一民，楊 飛*，代建云

(1.武漢大學電氣與自動化學院，武漢 430072；2.武漢大學土木建筑工程學院，武漢 430072)

錨桿錨固在工程應用中主要起支護作用，廣泛應用于各類土木工程，如邊坡、隧道、礦井等。自20世紀80年代起，以聲波反射法為基礎的無損檢測技術開始逐漸取代傳統的拉拔試驗法，成為了錨桿錨固質量檢測的主要手段[1-2]。在工程檢測中，錨桿埋入長度和灌漿飽和度被用于評判施工質量的好壞，而飽和度可利用入射信號與反射信號的能量比進行評估[2]，所以也須找到錨桿底端的反射波位置(即定位到了錨桿的長度)。目前,錨桿錨固質量檢測主要依靠操作人員的經驗，受人為因素的影響很大[3]。另外，因環境噪聲以及錨固系內部各類缺陷反射波混合疊加的影響，反射波形會發生各種不可預計的變化。這些都是導致錨桿長度和錨固的缺陷位置測量誤差大甚至根本無法檢測定位的主要原因。

利用Hilbert變換獲取反射信號的瞬時相位和瞬時頻率圖并進行分析，可以判定錨桿的缺陷位置和長度[4-6]。但使用該方法時，反射信號的相位圖中會出現多個相變點，需要操作人員具有高水平經驗來正確解釋數據。小波變換和經驗模態分解被用于對反射信號進行分解和去噪，并通過重構的反射信號來估算錨桿長度并檢測錨固缺陷位置[7-9]。但其更側重于反射信號的預處理，有助于信號異常點的提取。雷明等采用自相關分析方法開發了自動提取算法來測量錨桿長度[10]，該方法適用于高信噪比的反射信號，但當信噪比較低時測量準確度較低。

現提出一種基于相關函數的錨桿錨固質量無損檢測的數據處理方法，該方法利用互相關分析來輔助Hilbert變換進行錨桿長度和缺陷位置的精確測量。同時，綜合該方法和信號處理算法集成了一種新的錨桿智能檢測模型。

1 錨桿智能檢測模型

為從源頭上減少信號采集過程對檢測結果的干擾，通常會對目標錨桿重復進行多次敲擊和采集信號。在取得相當數量的波形數據后，首先對這些信號依次進行快速傅里葉變換(fast Fourier transform,FFT)頻譜分析，獲取信號主頻和帶寬信息后進行濾波去噪，然后利用近鄰聚類算法，對濾波后的信號進行對比篩選，從中選取最優、最好的一條信號作為原始的輸入；接著，分別采用廣義互相關算法和Hilbert變換對最優信號進行分析，最終獲得錨桿長度和缺陷位置，具體流程如圖1所示。

圖1 錨桿智能檢測模塊流程圖

1.1 去噪模型

去噪模型主要包括頻譜分析和濾波處理(圖1左邊部分框圖)，首先通過FFT獲取信號頻譜，獲得其主頻fc和濾波帶寬wn以用于設計合適的帶通濾波器。濾波處理采用有限長單位脈沖響應(finite impulse response，FIR)濾波器，具有嚴格的線性相位特性。若理想的數字濾波器的頻率響應函數為Hd(ejω)，則理想的單位脈沖響應[11]為

(1)

式(1)中:n為序列點數；ω為角頻率；j為虛數符號。hd(n)是一個無限長序列，無法設計適用于有限聲波信號的FIR數字濾波器。因為截斷信號會帶來截斷誤差，增加新的頻率成分并且改變譜值大小，從而導致頻率泄漏[12]。

針對這一問題，可以利用“加權”序列，也就是窗函數w(n)來修正，即

h(n)=hd(n)w(n)

(2)

窗函數的使用不能完全避免頻譜的泄漏，但可以有效地減少，因此FIR數字濾波時窗函數的選擇尤為重要。在工程上，選擇窗函數的三大原則分別為：主瓣窄寬帶；旁瓣低幅度，尤其是第一旁瓣；旁瓣幅度下降快速率[13]。通常上述幾點難以同時滿足，需要根據不同類型的信號選擇不同的窗函數。考慮到錨桿反射信號隨時間增長呈指數衰減的特點，文中去噪模型采用Gaussian窗函數，可有效提高信號的信噪比[14]。

1.2 錨桿信息提取模型

1.2.1 相關函數

若x(n)、y(n)是兩個能量有限的連續信號，并假設兩者呈因果關系，則有

(3)

在數字信號處理中，x(n)與y(n)的互相關函數定義為

(4)

x(n)的自相關函數定義為

(5)

1.2.2 信號篩選模型

聲波反射法采集的若干信號在經過FIR加窗濾波后，需要進行逐一對比，挑選出一條最具代表性的信號。首先采用式(4)，逐一計算n條信號兩兩之間的相關系數，可得n×n相關性矩陣R為

(6)

判斷矩陣R中是否存在元素rij>K，其中K為經驗閾值。若不存在，則表明此次采集到的所有信號無法用于后續分析；若存在，則使用近鄰聚類算法[16]將這些信號看作沒有類別標簽的樣本集{X1,X2,…,Xn}，若這些樣本可分為k類，其聚類中心依次為{Z1,Z2,…,Zk}，篩選最優信號的具體步驟如下：

Step1將樣本X1作為第一個類的中心，即Z1=X1。

Step2對剩下的樣本計算dist(Xi,Z1)，若小于相關系數閾值T，則Xi作為新的一類的中心Z2；否則，將Xi分配至第一個類，并將第一類的中心Z1更新為該類所有樣本的平均值。

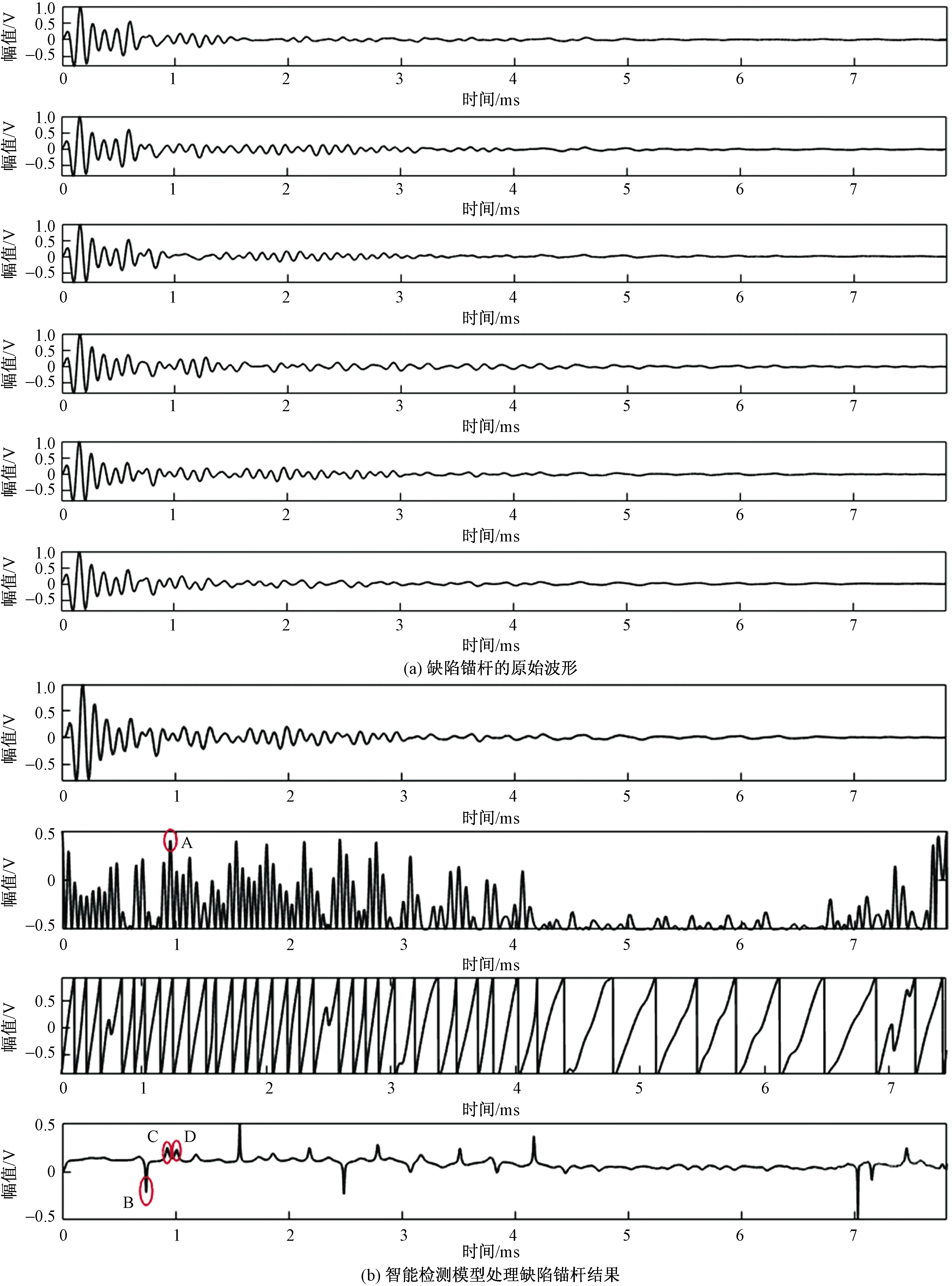
Step3將剩余的樣本分別計算dist(Xi,Z1)、dist(Xi,Z2)，若dist(Xi,Z1)

Step4按照上述步驟重復下去，直至將n個樣本分類完畢。

Step5分類完畢后獲得k個聚類中心，通過對比各聚類中心誤差平方和(SSE)得到最優類。已知誤差平方和公式為

(7)

式(7)中：k為類的個數；Zi是第i個類的聚類中心，dist(x,Zi)是指樣本x和Zi的相似度[17]。

Step6此時已知最優類的聚類中心Z以及包含的樣本{Y1,Y2,Y3,…}，計算dist(Z,Yi)并進行排序，獲得最優信號。

1.2.3 相關匹配模型

利用聲波反射法進行錨桿錨固質量檢測時，由于反射信號與入射信號間存在相似性，并且是周期性的。因此，可以通過分析反射信號與入射信號間的相關性，自動判別出桿底反射信號初始時刻的區間范圍。這里采用廣義互相關時差估計算法，利用加權函數來增強信號有效成分，進而提高時差估計精度，其原理如圖2所示。若x(t)、y(t)是兩個能量有限的連續信號，并假設兩者是因果的，則廣義互相關函數表示為

圖2 廣義互相關原理圖

(8)

式(8)中：ψxy(ω)為廣義加權函數；Gxy(ω)為信號x(t)與y(t)的互功率譜[18]。

首先從反射信號x(t)的首波起跳點處向后取2個周期的信號段作為入射信號y(t)，然后通過式(8)獲取到反射信號與入射信號的相關性信息后，搜索第二峰值點Tc，該點即為錨桿底端信號反射時刻范圍搜索中心。接著，再利用Hilbert變換提取信號瞬時頻率信息，在以Tc為中心，Td為半徑的時刻范圍內搜索距離Tc最近的突變點，可快速精確定位錨桿底端位置并計算出錨桿長度。同時，通過信號瞬時頻率信息也可定位并計算灌漿段的缺陷位置和長度信息。若在反射時刻范圍內未搜索到信號突變點，則將Tc作為錨桿底端信號反射時刻。

1.2.4 錨桿長度和錨固缺陷位置

假設信號在tx時刻發生突變，則被測錨桿的缺陷位置或長度l滿足表達式

(9)

式(9)中：l1為錨桿外露部分長度，可在檢測前測量；l2為錨桿埋入部分長度；tx為入射聲波突變點對應的時刻；t0為入射聲波首波對應的時刻；t1為聲波從桿頭傳播至孔口所用時間；C為聲波在錨固桿系上的傳播速度[7]。

2 實驗分析

為驗證本文提出的智能檢測模型的有效性，利用該模型對5根注漿模擬桿進行測試，圖3所示為實驗數據采集現場。剛灌注了混凝土沙漿的模擬桿實物模型如圖4所示，其桿體采用直徑20 mm的鋼筋，密實段為混凝土澆筑；空漿處為桿體外裹泡沫，并用膠帶封纏；外殼由長度2 m,內徑0.2 m的PVC管包裹。實驗使用自主研發的聲波檢測儀，配置磁致伸縮振源進行反射信號采集，采樣周期為2 μs，采樣長度為4 096點。在本實驗中：ωn=2 kHz，K=0.88,T=0.93，Td=100 μs。

圖3 模擬錨桿實驗

圖4 注漿后的模擬錨桿

圖5、圖6分別是對無缺陷錨桿和有缺陷錨桿采集的信號波形及利用智能檢測模型進行處理的波形示意圖，表1是采用智能檢測模型和常規的瞬時相位模型對模擬桿#1、#2、#3、#4、#5的反射信號進行處理的結果對比。其中圖5(a)和6(a)是對無缺陷錨桿和有缺陷錨桿采集的6條原始波形；圖5(b)和圖6(b)分別是利用智能檢測模型對無缺陷錨桿和有缺陷錨桿最優反射信號進行處理的結果，每組示意圖對應的四條波形從上到下依次是：從數字濾波后的6條信號中篩選出的最優信號、最優信號的廣義互相關信息、最優信號的瞬時相位圖、最優信號的瞬時頻率圖。通過以上實驗，對智能檢測模型的有效性進行分析：

圖5 無缺陷錨桿的信號處理與分析

圖6 缺陷錨桿的信號處理與分析

(1)觀測6條原始波形可知：采樣過程中，6次采集的波形都是有所不同的，如圖5(a)中有一條波形是明顯異于其他五條波形的。說明了在采樣過程中采集相當數量的信號并從中篩選出最優信號進行后續分析的必要性。另外，每條原始波形都不同程度地含有較強的噪聲干擾，由此可見，對采樣波形進行去噪是必不可少的。

(2)首先使用去噪模型對圖5(a)所示的6條原始波形進行濾波消噪，然后使用信號篩選模型從濾波后的6條信號波形中篩選出最優信號為第四條波形，也即圖5(b)第一條波形；最后，使用相關匹配模型對最優信號進行分析和特征提取。從圖5(b)第二個波形可知，廣義互相關處理后的波形的第二波峰時刻為A點對應時刻TA=0.618 ms，然后再以該點為中心，在圖5(b)第三、四個波形上查找突變點，可發現其附近有3個突變點B、C、D，對應時刻分別為TB=0.424 ms、TC=0.652 ms和TD=0.962 ms，TC時刻距離TA最近且在搜索范圍內，故利用式(9)，取桿系波速C=4 700 m/s可計算出錨桿長度為1.54 m。已知該無缺陷模擬錨桿外露部分長0.1 m，全長1.5 m，故錨桿長度檢測誤差為2.67%。

(3)利用去噪模型和信號篩選模型從圖6(a)中獲得最優信號為第5條波形，再使用相關匹配模型對其進行分析和特征提取。從圖6(b)第二個波形可知，廣義互相關處理后的波形的第二波峰時刻為A點對應時刻TA=0.946 ms，然后再以該點為中心，在圖6(b)第三、四波形上查找突變點，可發現其附近有3個突變點B、C、D，對應時刻分別為TB=0.702 ms、TC=0.900 ms和TD=1.012 ms，TC時刻距離TA最近且在搜索范圍內，利用式(9),取桿系波速C=4 700 m/s可計算出錨桿長度為2.123 m，缺陷B對應長度為1.658 m。已知該缺陷模擬錨桿外露部分長0.1 m，全長2.1 m，缺陷位置為1.59 m，故錨桿長度檢測誤差為1.10%，缺陷檢測誤差為3.24%。

(4)使用智能檢測模型和常規檢測模型對采樣數據進行處理，其中常規檢測模型是利用Hilbert變換獲取信號的瞬時相位圖來判定突變點位置[4-6]。通過表1中的數據對比可知，常規檢測模型在錨桿長度未知的情況下，對錨桿長度的檢測誤差不穩定且較高，而本文中提出的智能檢測模型的檢測結果誤差穩定且較低。

表1 智能檢測模型和常規模型處理結果對比

3 結論

對于長度未知錨桿在質量檢測中存在的檢測誤差大的問題，提出了一種基于相關函數的錨桿智能檢測方法，經過實際的工程檢測驗證，得到以下結論。

(1)對目標錨桿采集相當數量的反射信號，充分利用FFT、FIR、近鄰聚類、廣義互相關以及Hilbert變換這些信號處理算法，可從源頭上保證了數據采樣對分析結果的最低干擾，實現了在桿長未知的情況下，對錨桿底端反射位置和缺陷異常點的精確定位，從而實現對錨桿長度和灌漿飽和度這兩大施工評判標準的精準測量。

(2)實驗結果表明，采用智能檢測模型明顯優于常規的瞬時相位、瞬時頻率檢測模型，具有更好的缺陷檢出穩定性和更低的定位誤差率。

(3)將該智能模型算法集成到錨桿分析軟件中，可自動得出評判結果，整個測量過程可無需人工干預，不僅可以節約人力，還可有效地避免人為主觀因素的影響，實現檢測過程的智能化。