基于優化算法的移動機器人全局路徑規劃

何佳澤 張壽明

（昆明理工大學信息工程與自動化學院）

移動機器人同步定位與建圖（SLAM）中，需要規劃一條從起始點到終點的路徑，這個過程就被定義為全局路徑規劃［1，2］。傳統的A*算法是一種啟發式搜索算法， 它將整個地圖分成很多個節點，以評估節點的代價函數值來作為節點的綜合優先級［3］，通過遍歷周邊的節點，選取最高優先級的節點， 逐漸找到一條從起點到終點的最優路徑。 傳統A*算法在二維柵格地圖中的路徑規劃效果比較好， 它能快速找到代價最小的函數值，從而得到線路最短的路徑。 但是，因為它需要遍歷周邊節點， 所以在尺寸較小的地圖中比較實用。隨著地圖尺寸的不斷擴大，它將會搜索大量的無用節點，使得搜索的節點數量以指數級增長［4］。

為了使A*算法在尺寸較大的地圖中也能使用，筆者提出將它與啟發神經網絡（GBNN）模型結合，并使用跳點搜索（JPS）算法跳過下一個無用節點，減少整體計算量，從而提高算法的性能。

1 算法原理

1.1 A*算法柵格地圖全局路徑規劃

A*算法采用代價函數，通過不斷尋找周圍的節點，分析其代價規劃出一條最優路徑［5］，代價函數模型如下：

式中 F（n）——從起始狀態經由狀態n到目標狀態的代價；

G（n）——在狀態空間從起始狀態到狀態n的實際代價；

H（n）——從狀態n到目標狀態規劃的最佳路徑的代價。

A*算法是一種二維柵格地圖， 首先建立A*代價函數柵格地圖（圖1）。

圖1 A*代價函數柵格地圖

圖1建立的是5×5的柵格地圖，A*算法的基本原理是從起點開始遍歷周邊8個節點的代價函數值。 每一個柵格的長、寬都為10，根據對角線計算方法可知，柵格對角線距離為，近似為14；G（n）的值為起點到某一個柵格的最短距離［6，7］。筆者采用曼哈頓距離展開計算求得H（n）：

其中10為柵格的寬度。

求出起點周圍8個相鄰節點的代價函數值F（n），并且方向是朝著終點，（3，3）節點的代價函數值最小［8］，所以全局路徑規劃到（3，3），并且以此點為中心點， 計算周圍8個相鄰節點的代價函數值，選取下一個規劃路徑點，直到到達目標位置點為止［9］，如圖2所示。

圖2 A*算法代價函數規劃路徑

圖2中，起點到第2個節點最小代價函數值為54，然后是48，再到終點是42，由此得到一條最優全局路徑規劃。

1.2 A*算法的優缺點

A*算法由于原理簡單，在實際生產中得到了廣泛的應用， 但是它的缺點也同樣非常明顯，如果地圖比較大的話，它將會遍歷很多點，計算量特別大，并且每一個點的計算量也非常大，所以對系統的運算能力要求較高［10］。 為了彌補這兩方面的不足，筆者使用JPS算法與GBNN模型結合的方法來克服這兩個方面的缺點。

2 跳點搜索法

為減少中間無效節點和一些效果比較差的節點，筆者采用跳點搜索規則對每個節點周圍的可拓展節點進行篩選，跳過不需要拓展的節點［11］。 這樣就可以減少大量的節點運算，提高整體性能，進而提高搜索效率［12］。

水平方向和對角線方向的篩選規則如圖3、4所示。

圖3 水平方向篩選規則

圖3、4中灰色點代表不適合經過X節點建立全局路徑規劃的點， 白色點代表適合經過X節點建立全局路徑規劃的點。 圖3中路徑從X22節點朝著X點向地圖的右邊運動， 可以直觀地看出從X22到Y最短的路線是走直線：X22→X→X42→Y，直接經過X的路徑是最短的，如果繞過X，那么將不是最優選擇；如果終點Y是節點X51或者X53，那么經過X節點就不是最優路徑選擇， 此時的規劃路徑將不經過X節點。 同理在圖4中X22節點朝著X方向向Y節點運行， 搜索過程則可以直接跳過X節點。所以筆者根據圖3所示的水平方向篩選規則分成a、b兩種情況來篩選拓撲點（圖4所用對角線方向篩選規則同理）：

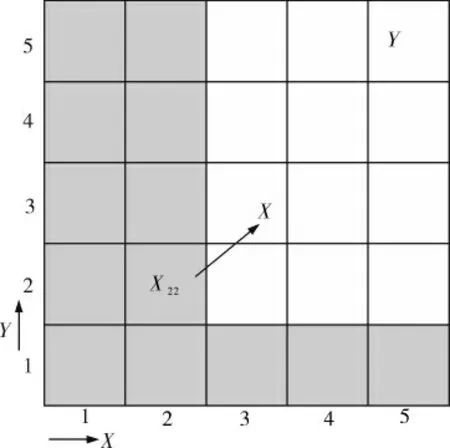
圖4 對角線方向篩選規則

a. 從X22節點向右側移動不經過X節點比經過X節點的路徑差的情況，如終點為X42或者X52；

b. 從X22節點向右側移動不經過X節點比經過X節點的路徑優的情況，如終點為X51或者X53。

情況a中X節點會加入到點集合中，情況b中X節點就會被去掉，這樣就可以去掉無效或者低效節點，減少節點處理量。

在沒有障礙物節點的環境中， 沿著X、Y方向的節點篩選規則為：

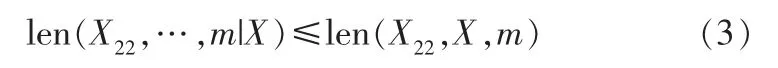
其中，m代表X可以拓展的相鄰節點，len（）代表路徑行進長度；（X22，…，m|X）代表不通過X而直接到m的最短路徑；（X22，X，m）代表X節點到達m的最優路徑。

同理，可以得到在沒有障礙物節點的環境中對角線方向的篩選規則：

3 A＊算法與GBNN模型優化

3.1 GBNN模型

GBNN模型是一種離散的生物啟發神經網絡，它不需要機器學習和深度學習。GBNN模型是三維立體神經網絡，主要用在水下機器人的路徑規劃中。 筆者通過簡化，構建了如圖5所示的二維神經網絡［13］，與二維柵格地圖一一對應。

圖5 簡化的二維GBNN模型

該算法的主體思想是不斷向四周傳遞激勵，障礙物對發散出的激勵有抑制作用，通過迭代算法計算出每個位置的活性數值。 該算法有記憶特性，地圖上的每一個點都可以通過不斷迭代到達激勵的發出點，這個激勵的發出點也就是路徑規劃中的終點［14］。

GBNN數學模型如下：

其中，Wij是兩個神經元i、j之間的連接權值，xi是i神經元的活性輸出值，Ii是i神經元的外部激勵值，ωij是i、j兩個神經元之間的連接系數，函數g是模型變換函數，γ、r為常數，根據情況設置。筆者采用的是二維柵格地圖，所以式（7）使用的是GBNN二維模型的歐拉公式，xix、xiy分別表示第i個神經元的x、y坐標值，通過式（7）即可求出i、j神經元之間的距離。

3.2 A*算法與GBNN模型結合

GBNN的二維神經網絡結構可以與路徑規劃中的柵格地圖一一對應起來，每一個神經元和一個平面二維柵格對應，它依據二維柵格地圖中各個柵格的狀態來決定神經元的外部輸入。 通過直接計算神經元的活性值來規劃路徑，這樣就可以避免大量代價函數計算， 減少節點之間的運算量。 GBNN模型不需要神經網絡學習， 不需要訓練，可以滿足路徑規劃對實時性的要求。

4 實驗仿真

筆者提出在A*算法的基礎上使用跳點搜索，這樣去掉不需要的低效和無效節點，然后在此基礎上加入GBNN模型。 模型構建以后，通過MATLAB仿真方法比較算法優化前后的效果。

實驗配置如下：

硬件 CPU i7-8750H

內存 16GB

軟件 MATLAB2016a

首先建立50×50的柵格地圖， 規定起點和終點的位置，隨機生成障礙物坐標，通過比較算法優化前后的路徑規劃時間、路徑遍尋節點數量和全局規劃路徑長度這3個指標來比較。

圖6為優化算法流程。

圖6 優化算法流程

圖7、8分別顯示了50×50的二維柵格地圖未使用和使用筆者所提算法的規劃路徑，圖中綠色圈為起點，藍色圈為終點，規劃路徑為藍色曲線。圖9、10分別對應圖7、8的運行時間、遍歷節點數和路徑總長度。

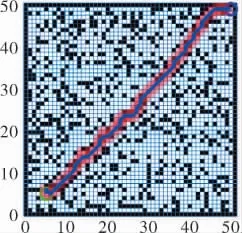
圖7 未使用優化算法規劃路徑

圖8 使用優化算法規劃路徑

圖9 未使用優化算法路徑規劃數據

圖10 使用優化算法路徑規劃數據

因為算法具有隨機性，為了使結果更具真實性，所以通過多次仿真實驗，比較算法優化前后的路徑規劃時間、路徑遍尋節點數量和全局規劃路徑長度的平均值，詳見表1。

表1 算法優化前后性能對比

通過表1可以看出優化后的算法對二維柵格地圖全局路徑規劃效果較好。

5 結束語

對傳統的A*算法進行優化， 加入JPS 和GBNN，將3種算法進行結合。 采用路徑規劃時間、路徑遍尋節點數量和全局規劃路徑長度這3個指標對算法的優劣性進行對比， 可以看出使用3種算法結合后的優化算法效果較好。