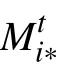百度遷徙規模指數構造方法反演

王 聰，嚴 潔

(1. 四川警察學院計算機科學與技術系 四川 瀘州 646000；2. 四川警察學院道路交通管理系 四川 瀘州 646000)

作為分析人口遷徙規律的重要工具，百度遷徙網站[1]提供了城市和省區間遷徙的人口比例和總體遷移規模估計，為COVID-19疫情防控提供了重要參考。然而，百度遷徙規模指數作為一個無量綱數，其構造方法并未公開，僅能從有限的信息推知該指數與實際遷徙人口可能存在正相關特征。目前國際疫情防控形勢仍不樂觀，輸入性疫情在國內仍時有局部性傳播。考慮到人類遷徙行為是COVID-19迅速傳播的主要驅動力[2]，從防范疫情全國性二次蔓延的立場出發[3]，分析百度遷徙的數據構造方法及與真實人類遷徙行為的對應關系，從中反推出遷徙行為的確切人數，可以為研究總結疫情防控規律提供有益參考。

來自移動通信網絡的數據是公共衛生管理的重要研判依據[4]。文獻[5]利用復雜網絡理論擬合人類遷徙與流行病學傳播的關系，發現相對于節點間的經緯度距離，疫情傳播與節點的等效距離相關性更強，而節點間的人類遷徙流量是等效距離的核心構成部分。因此，在COVID-19疫情爆發初期，考慮人類遷徙特征的流行病傳播研究就得到了廣泛關注。文獻[6]利用城市間航空流量數據和騰訊人類遷徙數據，以種群傳播模型進行建模。由于航空并非中國大陸出行的首選工具，該研究對疫情初期傳播過程的解釋能力存在缺陷。曾在區域經濟學[7]、城市經濟學[8]和人口地理學[9]等領域得到應用的百度遷徙網站也已重新開放，公開了百度依托移動互聯網采集的全國300余個地級市和30余個省(直轄市，自治區)的人類遷徙狀況。百度遷徙網站的數據陸續更新至2020年5月初，并保留1月10日-3月15日的數據以供參考。文獻[10]利用百度遷徙的數據初步調查了湖北省外部分城市遷入人口與疫情數據的關系，然而該分析僅局限于百度標注的流量較大的50個城市，相對于全國300余個地級市而言，覆蓋面有所欠缺。文獻[11]從百度遷徙數據中發現，各地累積確診量和自武漢流入的人口總數高度相關，且次生傳播鏈基本被斬斷，因此提出了一種考慮輸入病例和地區人口效應的定量化評估新型冠狀病毒地區防控效果的近似方法。文獻[12]利用百度遷徙的數據，對國內前50天疫情管控措施的有效性進行了細致分析，評估了旅行限制和社會疏導措施在防止傳染病傳播方面的效果。文獻[13]以百度遷徙數據為依據，分析了限制城際人口流動，篩查/診斷/隔離/疑似密切接觸者，以及社交隔離與個人安全防護等非醫學干預手段的效果。該研究指出，此類措施在付出高昂經濟代價的同時，可能使得患病人數減少了67倍。文獻[14]使用了百度遷徙公布的包括武漢市歷史與實時人口流動數據，以說明病例輸入在疫情城際傳播中的作用，并評估了防控措施的效率。文獻[15]則使用從百度遷徙數據中提取出武漢到河南的記錄，將河南省的輸入性病例視為對武漢市的無偏抽樣，以此估算出COVID-19在武漢的傳播情況。文獻[16]利用百度遷徙的數據，結合我國疾控中心的每日確診病例數據訓練SEIR模型，參考SARS的部分流行特征，利用LSTM神經網絡預測了COVID-19疫情在國內的峰值和演化趨勢。文獻[17]利用2020年1月10日-23日的百度遷徙數據分析了中國大陸的疫情空間格局特征，指出在省域層面疫情嚴重程度主要受鄰近特征與人口遷徙強度的影響。文獻[18]利用百度遷徙數據分析了疫情對中國城市人口遷徙的影響和城市的恢復能力。以上工作存在的一個共同問題是將百度遷徙規模指數假定為每日鐵路、公路和航空人口流量的近似擬合，而這一假設目前并沒有明確的依據。因此，本文前期工作[19]利用公開新聞報道中的春運數據，證實了遷徙規模指數與實際遷徙人數呈粗略線性關系，并給出了一個線性系數的大致估計，以此為依據分析了COVID-19在早期的時空傳播特征。

隨著疫情在全世界的蔓延，部分研究人員也利用人類遷徙數據研究疫情在國外的傳播與控制。文獻[20]使用了包含547 166次航班，總計101 455 913名乘客的人類遷徙數據集，分析了遍及六大洲22個國家的人口遷徙與疫情流行狀況的潛在關聯性，并建議在限制高感染地區人口流動的同時，亦應對全球范圍內的人口遷徙進行必要管控。涉及具體國家和地區的人口遷徙與疫情防控研究也普遍展開。文獻[21]使用了由Teralytics提供的2020年1月1日-4月20日匿名手機漫游數據捕獲美國每個縣的實時移動趨勢，利用這些數據來生成社交隔離評價指標，并結合流行病學數據來探索COVID-19的疫情增長規律；文獻[22]利用超過2 700萬個移動設備的漫游記錄，結合社交網站公開的數據，估計了美國不同區域社交隔離政策造成的地理和社會網絡溢出效應；文獻[23]將移動遷徙數據與人口普查統計數據相結合，建立了COVID-19在波士頓市區的精細傳播模型。文獻[24]利用一個包含意大利107個大區的人類遷徙網絡數據集估計了改進SEIR傳播模型的參數后指出，對人類遷徙與社交隔離的有效限制已將該國疫情嚴重程度降低了45%。文獻[25]利用社交網站提供的近似實時的意大利人口遷徙數據進行了大規模分析，以研究交通管制策略對個人和地方政府經濟狀況的影響；文獻[26]則關注了另一個疫情嚴重的國家巴西：通過航空數據的分析顯示，約76%的巴西毒株可能在2020年2月22日-3月11日期間自歐洲傳入，并主要在本地和本州內傳播。此后盡管航空旅行人數急劇下降，但大型城市的輸出效應不容忽視，當前該國的干預措施仍不足以控制疫情傳播。文獻[27]利用巴西數百萬匿名移動漫游數據分析了COVID-19在巴西各州內最可能的傳播方式，為公共管理計劃制定與資源分配提供了參考。人類遷徙數據同樣被應用于英國[28]和印度[29]等國家的疫情防控研究。

概覽近期文獻和成果，百度遷徙提供的數據已成為COVID-19疫情傳播研究的核心數據來源之一。然而可能出于商業原因，百度遷徙提供的反映遷徙人口絕對規模的指數僅為無量綱數，公開的信息僅能表明該指數的構成與人口遷徙量正相關，僅能回答如“區域A的在某日的遷徙規模指數相對于區域B高約1.25”，該指數代表的物理意義不夠明確，對于遷徙人口的絕對數量刻畫存在缺陷。考慮到流行病學模型對參量的敏感性，這一概要性質的表述限制了相關研究的可靠性。因此，有兩個問題是不得不回答的：1) 百度遷徙的數據與真實人類遷徙流量滿足什么映射關系?2) 如何從百度遷徙數據反推出真實的人口遷徙流量?

為了解答這兩個問題，本文首先概要闡述了百度遷徙的數據來源與獲取，然后以一個具體行政區劃為例，挖掘了百度遷徙數據中內蘊的一個恒等關系。在此基礎上，從理論上反演了實際遷徙人口和百度遷徙指數的函數表達式。基于費馬 - 歐拉定理(Fermat-Euler theorem)證明得到了真實遷徙人數的高概率互質特征，以此為基礎對映射函數的參數進行了有效估計，最終得到了一個自洽的線性函數映射模型。真實數據集上對內蘊恒等式的驗證結果支持了該模型的有效性。

1 百度遷徙數據概覽

百度慧眼是百度推出的一個商業地理智能數據平臺。作為商業數據中面向公眾開放的部分，百度遷徙網站展示了中國大陸省市兩級全部行政區劃的遷入/遷出遷徙規模指數以及與上一年度同一時間節點的對比，并針對每個行政區劃，分別按照地市級和省級級別提供了最熱門的100個遷入來源區劃和遷出目的區劃，以及遷自/遷入對應區劃的人口百分比。其遷徙邊界定義為某一區劃的行政管理地域，包括該行政區劃所管轄的所有下級區劃。

百度遷徙數據總體可以分為兩部分：遷徙規模指數和熱門遷徙區劃的遷徙人口百分比。百度將這兩個參量解釋為：1) 遷徙規模指數：反映遷入或遷出人口規模，城市間可橫向對比；2) 熱門遷入/遷出地比例：遷入/遷出到某城市的人口與全國遷入/遷出總人口的比值。

典型的百度遷徙數據的核心內容可以整理如表1和表2所示。

表1 人口遷徙百分比

表2 特定日期遷徙規模指數列表

其中，表1的核心數據是特定區劃遷徙人口的百分比。如表1的第一條目可解讀為：2020年1月1日自上海市遷入北京市的人口占北京市總體遷入人口的1.62%；表2的值項是指定區劃和指定方向的遷徙指數。如表2的第一條目表明，天津市在2020年1月1日的遷入規模指數為2.480 868。

2 百度遷徙數據中的內蘊等式

即遷徙規模指數與實際遷徙人數正相關。將遷徙規模指數的構造方法定義為真實遷徙人數的函數：

式中，以區劃 α的視角統計遷至區劃 β的人口數量，應等同于以區劃 β視角統計的自區劃 α遷入的人口數量。然后從真實數據中觀察是否存在其他等式。對美元流通數據[30]、手機信令數據[31]、GPS漫游數據[32]和小樣本的問卷調查[33]研究證實，群體視角下人類出行距離呈現出顯著的冪律分布，或帶指數截斷的冪律分布特征，出行人數隨出行距離增長將顯著衰減。因此同省內的區劃更有可能出現于彼此的Top100遷徙目的地中。寧夏回族自治區僅轄有5個地級市，是全國下轄地級市最少的省區之一，為縮短行文，在此將其作為示例進行考察。抽取2020年1月1日寧夏及所轄地級市的人口遷徙情況如表3～表5所示。

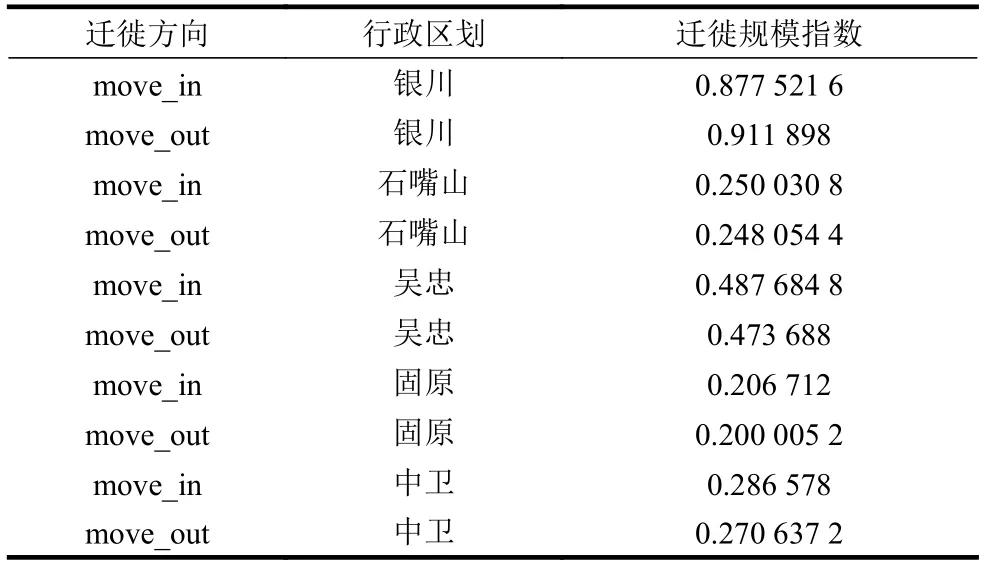
表3 寧夏所轄區劃2020年1月1日遷徙規模指數統計

其中表3可解讀如：2020年1月1日，銀川市遷入規模指數為0.877 521 6，遷出規模指數為0.911 898；表4可解讀如：銀川市遷入人口中有18.13%來自石嘴山市，有31.06%來自吳忠市；表5可解讀如：銀川市遷出人口中有17.32%前往石嘴山市，有32.04%前往吳忠市。

觀察發現，表3～表5中的內蘊等式為：

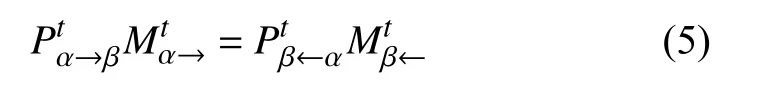
為校驗該內蘊等式是否成立，首先定義相對誤差RE(relative error)：

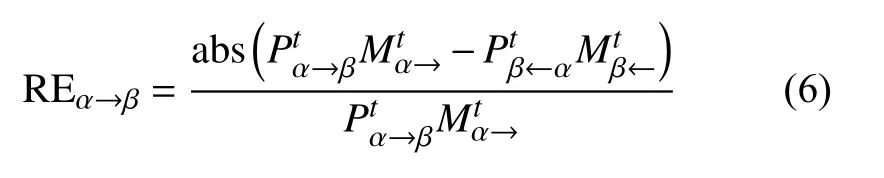
相對誤差RE的作用是評價遷徙數據相對于式(5)的偏離程度。將表3～表5的數據代入式(6)，以遷入數據為基準，得到以百分比表示的相對誤差統計如表6所示。

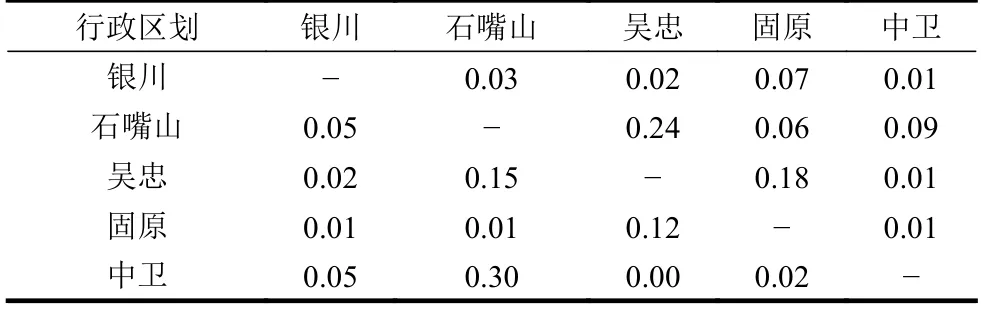
表6 寧夏所轄區劃2020年1月1日遷徙指數相對誤差統計 %

表中可見，最大的相對誤差值僅為0.3%，平均相對誤差也僅為0.07%。因此，從小樣本數據來看，可以認為內蘊等式得到了有效驗證。

3 遷徙規模指數構造反演與參數估計

3.1 遷徙規模指數構造過程推導

注意到式(1)對遷徙規模指數特征的刻畫仍是極為粗略的，滿足該式的函數形式也不是唯一的。因此有必要推導出遷徙規模指數的確定表達式，即式(2)的確切形式。

將式(2)代入式(5)，可得：

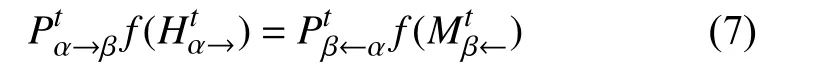
即，遷徙規模指數可表達為實際遷徙人數的線性函數。

3.2 參數估計

在爬取的數據中，遷徙指數至多保留至小數點后7位，因此首先排除遷徙指數上的舍入誤差問題。考慮人口遷徙的隨機性，若指數存在舍入誤差，則尾數的最后一位的取值應近似服從均勻分布。抽取2020年1月-4月遷徙規模指數共95 590條，最后一位實際取值分布如表7所示：

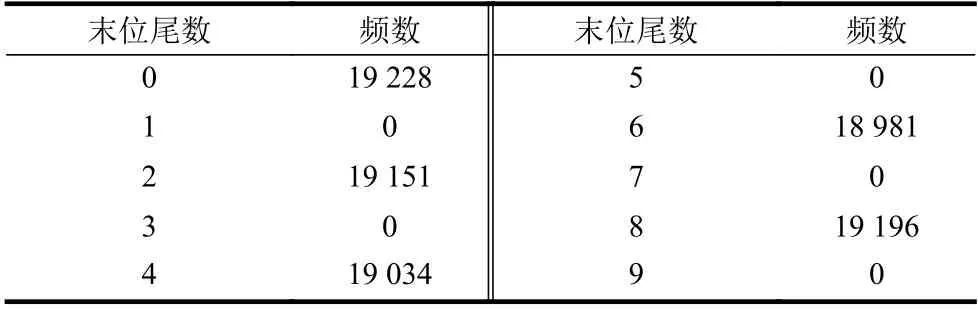
表7 遷徙規模指數尾數統計

其中，原生數據中小數點后有效數字不滿7位的取值，以0補足。表中可見末位尾數全部為偶數，難以滿足均勻分布推論，不應認為是偶然因素所致。因此有理由認為爬取的指數是一個精確的數值，可以排除舍入誤差問題。

對181 701條遷徙規模指數記錄(包含2020年數據，及對應的2019年歷史數據)進行統計，其中僅包含44 703個不同的取值。因此有理由認為，該指數的取值是離散的，即推論1是成立的。于是將44 703個出現過的指數值進行排序并取級差，結果如圖1所示。

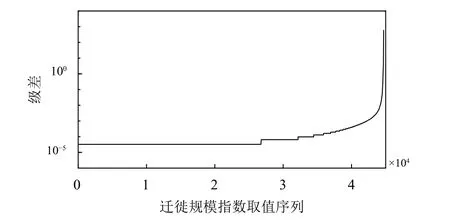
圖1 遷徙規模指數取值級差

圖中可以看到鮮明的離散特征，即不同取值之間的差值集中在有限個離散的值上，這為推論2的成立提供了可靠的依據。更為關鍵的現象是，無論是級差還是遷徙規模指數取值，都是最小間隔3.24×10-5的正整數倍，有理由認為是一個或多個自然人在遷徙規模指數上映射的結果。

接下來討論實際遷徙人數的互質特征。根據費馬-歐拉定理，s條記錄值互質的概率P(s)可利用黎曼 ζ函數(Riemann ζ function, 當s為正整數時，ζ(s)退化為歐拉乘積公式)表示為[34]：

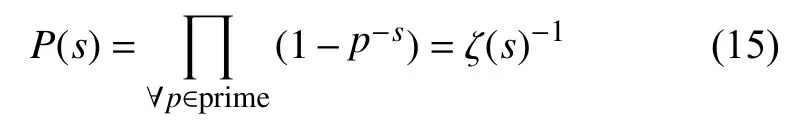
式中，p的值域被定義為質數集合。根據 ζ函數性質可知，當s≥1時 ，P(s)單調遞增。特殊地，當s為正偶數時，ζ (s)的取值可解析地表達為：

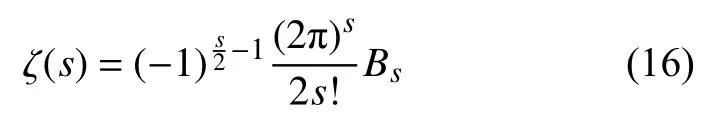
式中，Bs為第s項伯努利數(Bernoulli number)。

當s=10時，P(s)的值收斂至約99.9%；當s=14時，P(s)收斂至高于99.99%。即隨機抽取不少于14條不同的遷徙人口值，其互質的概率超過99.99%，且隨著抽取記錄數量的增加，這一概率仍會進一步提升。而統計得到指數的取值高達4萬余條，因此有理由認為，遷徙指數記錄所代表的實際遷徙人數極高概率是互質的，其最大公約數為1。因此，可以認為當一個自然人映射到遷徙規模指數上時，有：

于是，將斜率k代入式(13)，可得任一方向上百度遷徙規模指數的構造方法為：

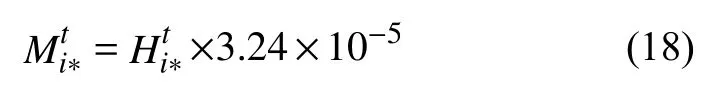
4 數據獲取方法

4.1 數據訪問接口

通過對百度遷徙網站Web頁面的分析可知，遷徙規模指數數據來自接口：http://huiyan.baidu.com/migration/historycurve.json，該接口以HTTP GET方法訪問，并攜帶必要參數如表8所示。

表8 遷徙規模指數數據訪問必要參數

其中的id參數定義為以國家標準GB/T2260-2007定義的中華人民共和國行政區劃代碼[35]，涵蓋了所有省級區劃及其(除直轄市)直管的下級區劃。正常情況下返回JSON格式文本形如：

其中的有效數據為list字段，記錄了2020年春運期間特定區劃在特定日期的遷徙規模指數，以及以農歷日期對齊的2019年同期數據作為對比。

地級市遷徙人口比例數據來自接口：

http://huiyan.baidu.com/migration/cityrank.json

省級遷徙人口比例數據來自接口：

http://huiyan.baidu.com/migration/provincerank.j son

以上接口以HTTP GET方法訪問，并攜帶必要參數如表9所示。

表9 遷徙百分比數據訪問必要參數

正常情況下返回JSON格式文本形如：

其中有效數據為list字段。"city_name"等字段以Unicode轉義字符形式編碼，使用時應進行解碼。

4.2 數據污染與有效性校驗

百度遷徙網站一種可能的反爬蟲策略為隨機投放污染數據。舉例而言，本文初次爬取的三亞市在2020年2月2日遷出至地級市的數據即可能存在污染。與真實數據對比如表10所示。

限于篇幅，表10僅枚舉前3位數據。因此為了確保爬取數據的準確性，采用了一種主-從爬蟲框架，首先確保主從節點使用不同的IP地址，由主節點按日期爬取數據并進行校驗。對于校驗失敗的數據，交由從節點重新爬取，以避免主從節點同時被遠程主機屏蔽。

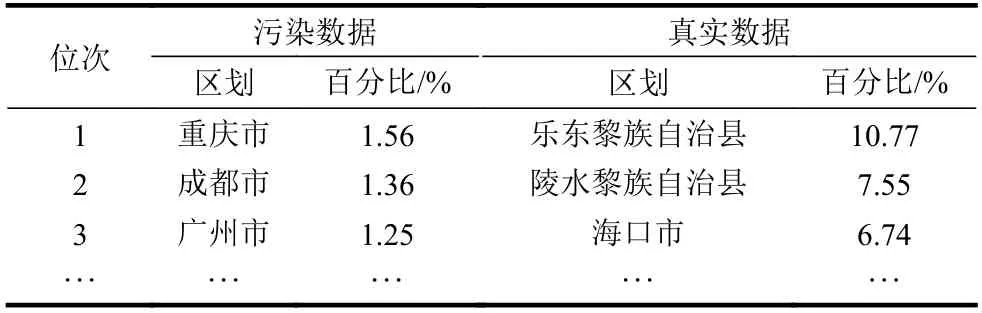
表10 污染數據與真實數據對比示例

5 內蘊等式有效性驗證

首先考察市際遷徙流量是否滿足本文提出的線性關系。在數據中，北京、上海等4個直轄市，以及湖北省潛江市、天門市和新疆維吾爾自治區石河子市、圖木舒克市等直轄縣級行政區劃均被納入城市區劃進行采集和統計。數據中，約93.81%的記錄誤差位于舍入誤差區間內，異常記錄僅占約6.19%。意味著在城市間交通流量這個層面，線性映射模型的基本假定可以得到滿足，數據測量誤差對于函數映射模型有效性的影響是有限的。正常記錄、異常記錄和全部記錄的相對誤差累積分布如圖2a所示。圖中可見，大約81.2%的記錄相對誤差在5%以內；而由于異常記錄占比較低，過濾異常記錄后，這一指標微升到82.8%。對于異常記錄而言，這一百分比則有51.1%。然而僅僅考察相對誤差是不夠全面的，誤差的絕對差值，抑或就本文述及的模型而言，誤差的絕對人口數，也是評價模型有效性的重要指標。定義絕對誤差AE(absolute error)：

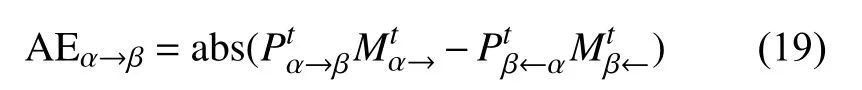
遷入流量的絕對誤差與式(19)類似，不再贅述。絕對誤差的含義顯然是經由線性映射模型換算后城市 α和 β統計視角下遷徙人口的差值。圖2b是正常節點絕對誤差統計直方圖。圖中可見，對于正常記錄而言，當不考慮舍入誤差時，有約87.44%的記錄絕對誤差不多于3人；約93.44%的記錄絕對誤差不多于5人。絕對誤差的極值出現在1月20日：當日汕頭視角下自深圳遷入人口及對應的反向記錄的誤差達到了79人的極值，但對應的相對誤差僅為0.48%。因此有理由認為，相較于測量誤差，舍入誤差具備壓倒性的影響。當考慮舍入誤差時，遷徙人數的取值將松弛為某個特定區間，因此記錄的絕對誤差顯著減小。圖2c統計了異常記錄絕對誤差人數。圖中可以看到，即使是異常記錄，其最大絕對誤差人數相對于舍入誤差區間也僅偏出36人。在異常記錄中，有82.98%的記錄誤差人數在3人以內，有98.65% 的記錄絕對誤差人數在10人以內。可見，少量的違例現象對線性映射模型不產生本質影響，將其假定為數據測量誤差是自洽的。

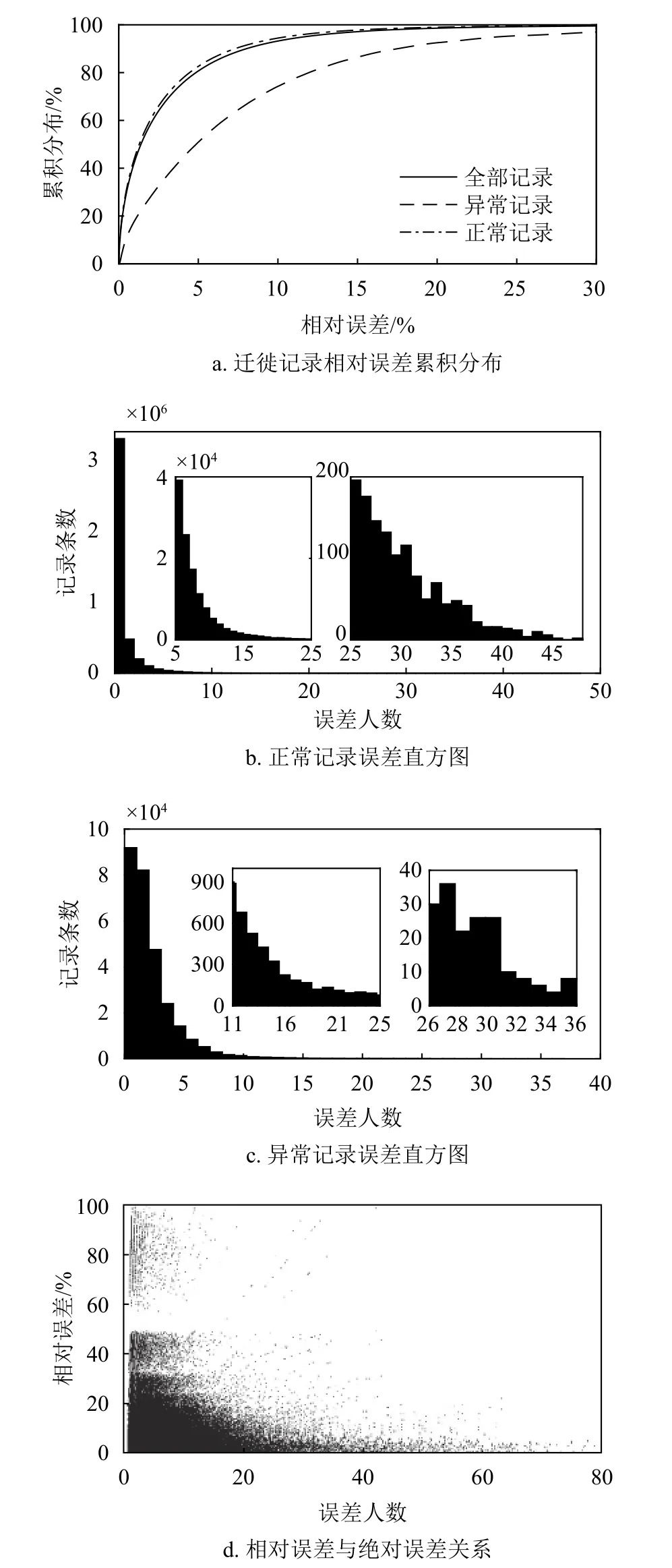
圖2 市際遷徙流量校驗

注意到一個現象，即較多的絕對誤差人數未必對應于較高的相對誤差。因此，通過圖2d分析異常記錄的相對誤差和絕對誤差的對應關系。該圖可分為4個邏輯象限：高相對誤差高絕對誤差；高相對誤差低絕對誤差；低相對誤差高絕對誤差和高相對誤差高絕對誤差。在圖中，高相對誤差高絕對誤差區域幾乎為空白。此外，除在低相對誤差低絕對誤差象限集中了大部分記錄外，另外兩個象限也存在一定比例的記錄分布。分析可知，當兩地人口遷徙流量懸殊時，以低流量區劃視角統計的記錄易出現高相對誤差低絕對誤差的情況：而兩地人口流量均較大時，則易出現低相對誤差高絕對誤差的違例數據。

市-省間遷徙流量數據同樣可以印證線性映射模型的有效性。利用與市際遷徙流量相同的統計方法進行分析。如圖3a，有82.65%的數據記錄誤差位于舍入誤差區間內。該數據雖較城市間流量數據偏低，但全部記錄的相對誤差同時亦有顯著降低：有約92.06%的記錄相對誤差不高于5%；這一指標在正常記錄中達到了97.13%，在異常記錄中同樣達到了77.3%，說明在市省流量層面的測量誤差影響同樣是有限的。圖3b是正常記錄的絕對誤差統計。其中有73.86%的絕對誤差人數在3人以內，有95.77%的絕對誤差人數在10人以內。在正常記錄中誤差人數極值為97人，出現于1月20日北京市視角下自廣東省遷入人數，此時相對誤差為1.32%，仍處于舍入誤差松弛區間。如圖3c，當將考察視角遷移到異常記錄時，發現擦除舍入誤差后最大誤差人數為250人，出現于1月17日濮陽市視角下自山東省遷入數據，此時對應的相對誤差也僅為2.64%。注意到即使僅考慮異常記錄，也有約98.6%的絕對誤差人數仍不多于50人——對于少則數百萬，多則近億人口的省級行政區劃而言，可以認為這個量級的測量誤差影響仍是有限的。相對誤差與絕對誤差的對應關系如圖3d所示。可見在市-省層面表現出了與市際遷徙相似的分布特征，但其低相對誤差低絕對誤差象限的記錄更加貼近相對誤差坐標軸。一個合理的解釋是，省級區劃的遷徙記錄來自下轄市級區劃對應記錄的簡單加和，因此下屬區劃間測量誤差的累積會抬高絕對誤差；但由于測量誤差存在部分相互抵消的現象，而市級區劃的流量基數不變，因此隨著遷徙流量的累加，相對誤差反而會有所下降。

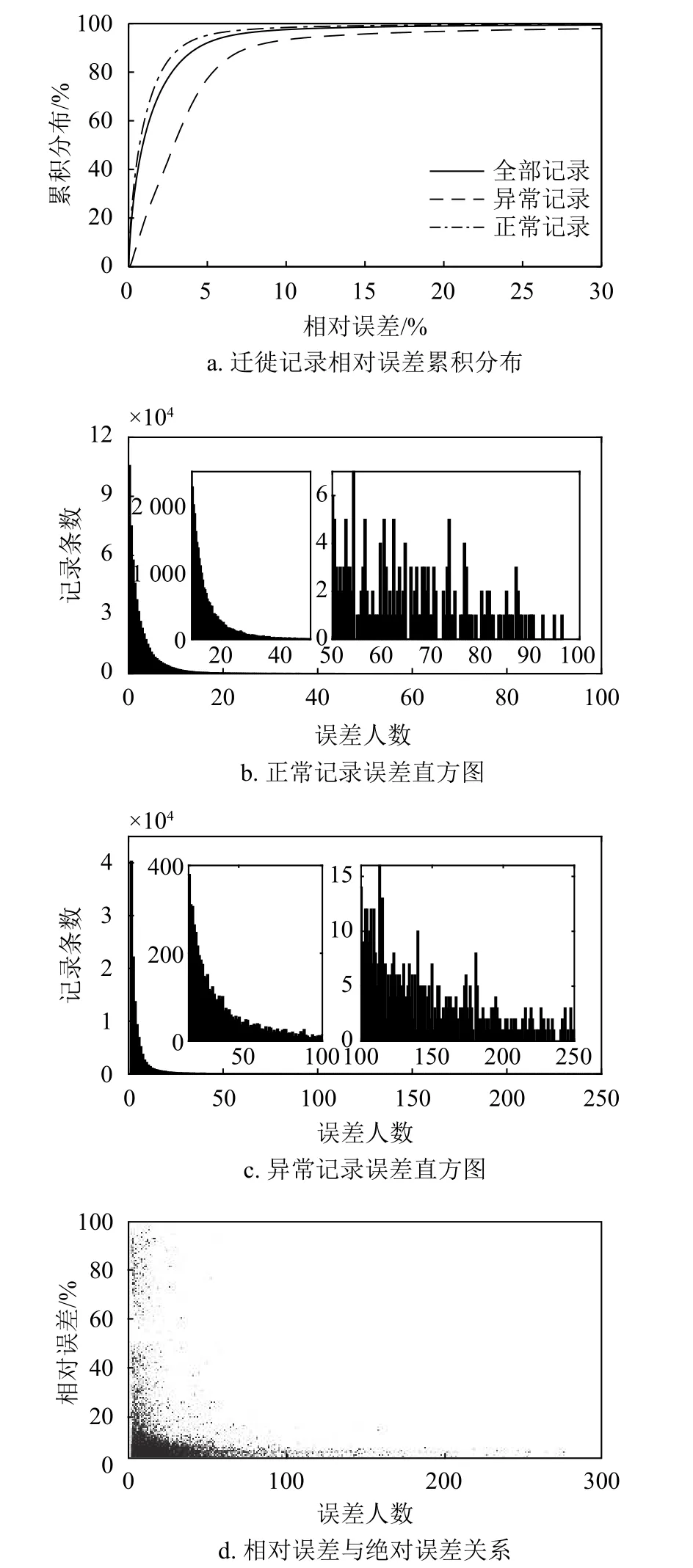
圖3 市-省遷徙流量校驗

將同樣的分析方法應用于省際遷徙數據進行驗證。在圖4a中，有84.87%的記錄誤差可被舍入誤差區間覆蓋。同時，由于記錄兩端的節點均為省級區劃，人口遷徙基數較大，降低了遷徙記錄的相對誤差：有50.73%的記錄相對誤差小于0.5%；89.43%的記錄相對誤差小于5%。圖4b與4c分別統計了正常記錄與擦除舍入誤差后異常記錄的絕對誤差。可以看出，即使在省級區劃這個層面，絕對誤差仍可控制在相對很低的水平。對4個月的遷徙記錄統計顯示，正常記錄中的極值出現于1月12日江西視角下自廣東遷入記錄，與其對應的反向記錄差值為107人，對應的相對誤差僅為0.05%。異常記錄中的極值出現在1月23日北京視角下遷往山東的記錄及對應的反向記錄，此時絕對誤差達到357人。相對于兩地當日該方向上70 871～71 337人的遷徙人數而言，其相對誤差僅為約0.5%。如圖4d所示，相對誤差與絕對誤差的關系也體現出與市際流量和市省流量相似的特征。但隨著流量基數的增加，低相對誤差高絕對誤差象限匯聚了相對更多的記錄。總的來看，省際遷徙流量的數據同樣可以給予線性映射模型有力的支持。

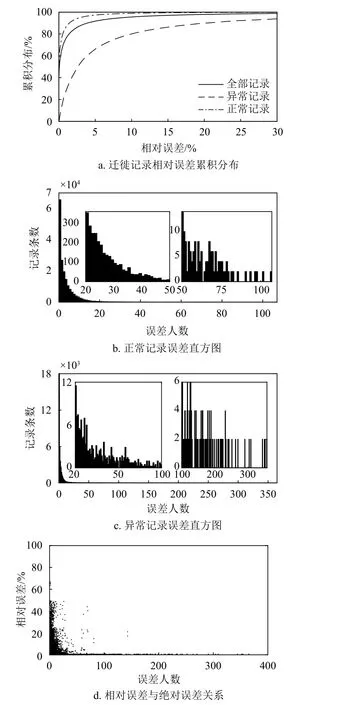
圖4 省際遷徙流量校驗

6 結 束 語