學材再構建，溫故而知新

甄慰

復習課是幫助學生“再學習”的一種載體。一節復習課的好與差，不僅會影學生的復習效果，還會影響學生系統知識的構建及學習能力的提升。日常的復習課，教師容易以“炒冷飯”的方式來梳理知識或是“題海戰術”方式以練代講。在復習課中如何實現知識的內化和升華，使復習課具有獨特的教學價值？下面，以廣州市教育研究院楊健輝教師指導的小學數學五年級上冊《多邊形面積計算》復習課教學為例，談談復習課的學材再構建。

一、變中重構，融會貫通

多邊形的認識和面積計算，分散安排在不同年級的教材中，雖成獨立單元，但系統性不太強，不容易揭示知識之間的內在聯系。三角形的面積、平行四邊形的面積、梯形的面積在學生的印象中就是幾個互不相干的公式。可以通過公式的再現，在“變”與“不變”中，讓學生真真切切地感受到各公式間的緊密聯系，融會貫通。

例如：

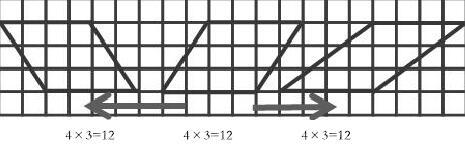
（1）依次出現方格圖中三個平行四邊形，研究保持數據不變（底、高），其某條邊整體變動而面積保持不變的道理。

4×3=12? ? ? ? ? ? ? ? ? 4×3=12? ? ? ? ? ? ? ? ? 4×3=12

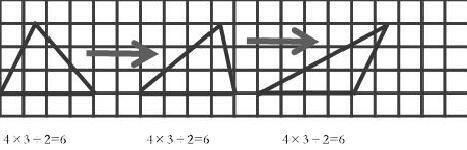
（2）依次出現方格圖中三個三角形，研究保持數據不變（底、高），其頂點變動而面積保持不變的道理。

4×3÷2=6? ? ? ? ? ? ? ? ? ? ?4×3÷2=6? ? ? ? ? ? ? ? ? ?4×3÷2=6

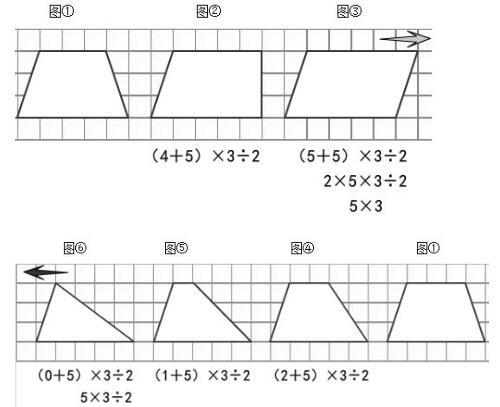
（3）從梯形出發，使其一條底邊長度發生變化引起圖形面積數值的變化，嘗試溝通三組公式之間關系。

《多邊形的面積》這個單元除了公式推導時層層遞進，共同利用轉化的方法之外，還有一個內在聯系——梯形面積公式，但在知識背后的橫向聯系，學生很難發現。展示梯形的一條底邊長度發生變化過程，將梯形的面積公式與其它圖形的面積公式進行整合，讓學生發現，看來貌似八竿子打不著邊的、完全不關聯的梯形的面積公式是其它三種圖形面積的通用公式，給公式新的含義。從而使學生的認知結構在新的建構中得到新的生成、伸展和生長，培養學生更好的數學思維品質。

二、多次轉化，思中得慧

轉化思想不僅是一種基本的數學思維，同時也是促進學生諸多數學思維培養的催化劑。多邊形的面積計算是以長方形面積計算為基礎，以圖形內在聯系為線索，以未知轉化為已知的基本方法開展學習（將平行四邊形轉化為一個長方形、將三角形學過的長方形、正方形、平行四邊形推導出面積計算公式、將組合圖形轉化為基本圖形），滲透轉化的思想比較單一。因此，本課借助以下題組來引導和促進學生對轉化思維的進一步應用：

例如：

（1）一個長方形（如下圖）的長是12厘米，寬是5厘米。A、B兩點是上、下兩邊的中點，這個平行四邊形的面積是多少？

方法一：長方形的面積減去兩個三角形（三角形的底即長方形長的一半，高即長方形的寬）;方法二：直接找數據算平行四邊形面積（底即長方形長的一半，高即長方形的寬）;方法三：平行四邊形通過等積變形轉化成長方形面積的一半。

（2）一個直角梯形（如下圖），已知涂色的三角形面積是48平方厘米，求梯形的面積。

方法一：先求小三角形面積（梯形的上底即三角形的底，梯形的高即三角形的高），再加上大三角形;方法二：先求大三角形的底邊（即梯形的下底），再求梯形面積。

數學的本質是思維。讓學生在思考中獲得思考的經驗，從而發展其思維、啟迪其智慧，是數學教學的重要價值所在。片段二中題組解法多種均不是此題組的目的所在，而是在借助圖形的轉化、數據的轉化、關系的轉化去突出圖形之間的聯系，從而去求得多邊形的面積。這一過程中，讓學生充分體會到轉化的魅力，對轉化思想有一個更深刻的理解，促進學生整體認知水平的發展。

三、錯例再現，辨中嘗新

學生在之前的單元整理和復習中，已進行系統整理知識，彌補學習缺陷。但在總復習，更強調在原有知識的基礎上體現提高、發展，促進認知結構的完善。本課作為一節期末總復習課，其中要包含的要素有：對計算公式的理解、計算方法的融合、計算技能的熟練及復習應考的準備等。因此，以往的錯例便是最好的資源。

例如：

（1）下圖三角形的面積是：6×4.8=14.4平方厘米。

（2）一個平行四邊形的底是4厘米，高是9厘米，它的面積是36平方厘米;與它等底等高的三角形面積是72平方厘米。

（3）工地上有一堆鋼管，橫截面是一個梯形，已知最上面一層有2根，最下面一層有12根，共堆了10層，這堆鋼管共有140根。

題（1）看似計算錯誤，實則是底和高之間的對應關系反復強調也是重復出錯，錯在“不對應”，但根源是在三角形的高的概念上。辨析中，學生借助三角形的高就是“從頂點到底邊的垂線段”，再次對“頂點”“底邊”和“高”之間的關系進行辨析。理清三角形底和高的對應關系本質是頂點和它的對邊以及它們間的對應關系。

題（2）看似考查三角形面積和平行四邊形面積之間的關系，實則是三角形面積公式的推導過程欠清晰。回顧三角形的面積=底×高÷2，“底×高”求出了什么？“÷2”又是什么意思？——平行四邊形是由兩個完全一樣的三角形拼起來的，平行四邊形的面積是最初的三角形面積的2倍。

“錯點”是鮮活的教學資源，學習過程中總有計算錯誤存在。因此，在復習課中，把這個錯例作為一個再學習的內容讓學生開展研究，使這些錯誤發揮新的作用，引導學生去“找錯”，培養學生“析錯”“糾錯”的能力、反思意識，提升數學素養。

舊知識的再現并不是簡單重復以前的學習內容，本課對公式、轉化、錯例等“再學習”的真正意義所在是使圖形之間的整體關系、計算方法與思考的聯系、復習補差與考題嘗新的關系、公式的運用與數學本質的關系等進行深度整合。

復習是學生對所學知識的再學習、再認識、再整合的過程，是進一步鞏固基礎知識、優化思維、提高能力的重要階段。作為數學教師，我們應以復習課為載體，讓學生在“再學習”的過程中能夠形成更加條理化、系統化的知識體系。完善知識結構，促使學生自身數學能力得到有效的發展和提升。