排污權價格不確定情境下企業生產決策的均值-方差模型
金 帥 ,牛藝霏 ,吳蘇閩
(1.江蘇大學 管理學院,江蘇 鎮江 212013;2.南京大學 社會科學計算實驗中心,南京 210093)
近年來,考慮排污權交易的企業生產運作研究已經成為運作管理領域的熱點,并涌現出不少探索性成果。Dodos[1]和Li[2]基于Arrow-Karlin模型,通過假定排污權價格服從特定已知隨機過程,研究了多期排污權交易下實現生產與庫存成本最小化的企業最優動態控制問題。杜少甫等[3]將排放權視為企業的一種資產和生產要素,從運作層面考察了排污權交易對企業單期生產策略的影響及其優化問題。其后,也有學者從考慮產品市場隨機需求[4-5]、消費者偏好[6-7]、排污權交易市場因素[8-9]以及納入供應鏈運作場景[10-13]等不同角度進行了拓展與深化研究。然而,相關研究尚集中在基于排污權價格確定情境的探討。
相比而言,面向排污權價格不確定情境的生產運作研究并不多見,典型文獻有:Gong等[14]將排污權價格隨機情境引入生產運作研究,并考察了擁有清潔與常規兩種生產技術的制造商實現有限規劃期內貼現成本最小化的生產規劃策略;Song等[15]運用兩階段隨機模型探討了存在碳排放約束的制造商的最優產能擴張與生產問題;易永錫等[16]從預期成本現值最小化視角運用實物期權法分析了排污權價格不確定性對企業污染治理投資決策的影響;Pommeret等[17]則關注于總量約束隨機變動引致排污權價格不確定,從跨期污染控制成本最小化視角研究了企業清潔技術投資與治污決策以及排污權銀行機制的影響。值得一提的是,上述研究關注排污權價格不確定情境下實現污染治理或生產成本最小化的特定環節跨期決策問題,有必要將生產運作諸環節結合在一起從整體收益層面進行綜合考慮[3];特別是,現有考慮排污權價格不確定性的研究均是基于風險中性假設,而且,即便面向產品隨機需求情境的相關研究也鮮有考慮到企業決策風險及其對決策行為的影響。
事實上,由于受市場機制及其外界不穩定環境(如宏觀經濟、環境政策、減排配額等因素)的影響,排污權市場價格具有顯著的波動性,排污權本質上是企業的一種風險資產。行為運作管理的相關研究也表明,決策主體在面對不確定性時并不完全遵循風險中性假設,而是會納入對風險的考量[18]。由此可見,研究如何有效測度排污權價格不確定性所引致的企業決策風險、建立考慮風險的決策優化模型,具有重要的理論意義和實踐價值。然而,相關研究更少見,金帥等[19-20]分別探索運用前景理論分析框架與CVaR 準則,探討了實現前景效用最大化與隨機利潤CVaR 最大化的企業生產決策,但卻忽視了對于排污權價格不確定情境下企業隨機利潤性質的論證,也缺少對于決策者在決策時對期望利潤考量的關注,而現實企業決策制定往往是基于對期望利潤與風險的綜合權衡所作出的。
鑒于此,基于現有研究成果,本文面向“排污權市場價格不確定”這一客觀情境,探索引入金融風險管理的經典工具——均值-方差模型,建立對企業生產決策風險和回報的基本測度,剖析考慮風險并兼顧期望利潤的生產優化問題,揭示排污權價格不確定性對生產決策的影響及其機理,以期彌補現有相關研究的不足,并為企業生產決策制定、宏觀調控與體系優化等提供理論依據。
1 基本假設與參數
采納文獻[3-4,8-19]中的基本模型架構,主要考慮單污染物排污權交易管制下排放依賴企業在排污權市場價格未知情形下的單周期生產決策問題,如圖1所示。
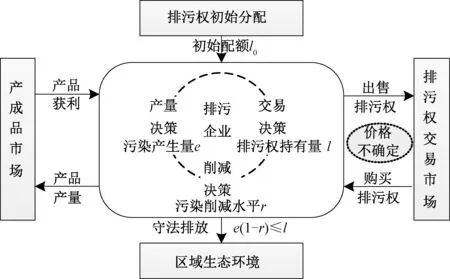
圖1 排污權價格不確定情境下企業生產決策分析框架
結合現實情況,做出如下假設:
假設1考慮企業具有污染排放依賴性且守法,在確定技術水平下,其污染產生量是產量的增函數。由此,可將其產量獲利記為污染產生量e的函數B(e),且滿足B(e)連續可微,B(0)=0,B'(0)>0,B″(e)<0,即生產的邊際收益遞減[8]。進而記理性企業在無規制情形下的最大產污量為,即B'()=0。此外,企業單位污染削減成本是其削減水平r(0≤r<1)的函數C(r),且滿足C(r)連續可微,C(0)=0,C'(r)>0,C(1)→∞,C″(r)>0,即C(r)隨r的提高而加速上升[3]。
假設2單位排污權對應單位污染合法排放權利。排污權可在市場中自由交易,且無交易成本與市場支配力,但不能存儲與借貸排污權[8]。記企業初始分配獲得的排污權數量(即初始配額)為l0。
假設3企業是排污權市場價格接受者,在生產計劃制定時排污權市場價格P未知。根據先驗信息可知,P是一個非負連續隨機變量,均值與標準差分別為μ與σ,概率密度函數f(P)非負可積[19]。
2 基本模型建立與分析
基于假設1、2可知,為了履行總量控制下的減排責任,守法企業的排污權持有量l不得少于其排污權占用量,即l≥e-er;且因排污權不能存儲與借貸,所以企業的理性選擇為l=e(1-r),進而其排污權交易量t=l-l0。其中:t>0意味著初始配額不足,需要購買;t<0則表明需要出售剩余;而若t=0,則無需交易。由此可得企業凈收益函數:
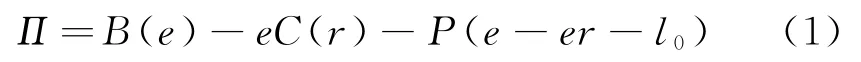
2.1 排污權市場價格追隨者的最優生產決策特征
面向排污權市場價格不確定情境建模,首先要厘清作為價格追隨者的企業對排污權市場價格的最優反應。根據上述假設與分析,可將任意給定排污權市場價格p下的企業最優決策模型化為:
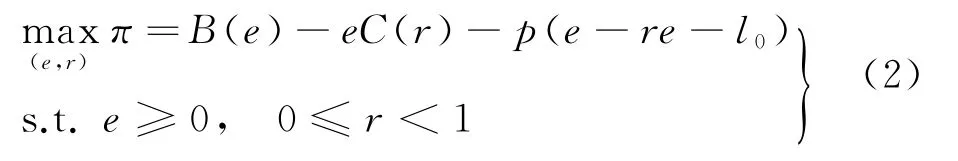
命題1在任意排污權市場價格p下,作為價格追隨者的企業最優生產策略,包括最優產量e*、削減水平r*、排污權持有量l*與交易量t*及其最優收益π*等,均與p密切相關,且滿足:
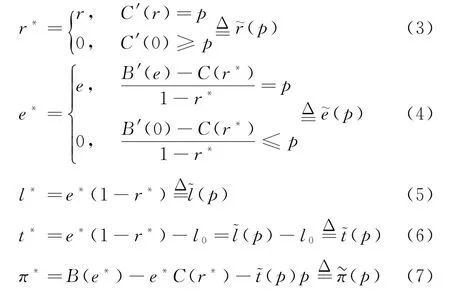
采用拉格朗日乘子法易證得命題1。在關于排污權交易市場支配力影響的研究[8]中已有類似論證與闡釋,不再贅述;但是文獻[8]中缺乏對最優決策性質的剖析。命題1較好地體現了排污權交易規制區別于傳統環境規制的顯著特征,即排污權市場價格成為衡量企業決策是否成本效率的重要標準。由式(3)、(4)也不難發現:①僅當p>C'(0)時,企業適宜削減污染(r*>0);②僅當p<[B'(0)-時,企業開展生產(e*>0)才有利可圖。
下面重點分析最優決策及其結果的相關性質。首先,由C(r)與B(e)均連續可微易知:
性質1及都是在[0,∞)內關于p的連續函數,其中:當p=0時當p≥pmax時,
其次,依次對式(3)~(6)進行全微分,整理可得:
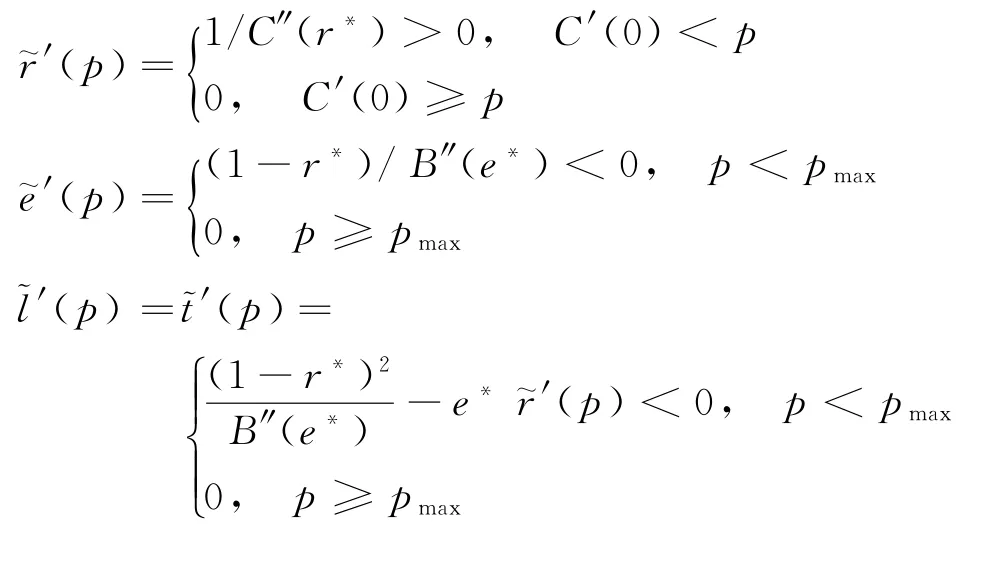
由此可得:

性質4若將最優決策下企業在產品生產與污染削減環節的凈收益
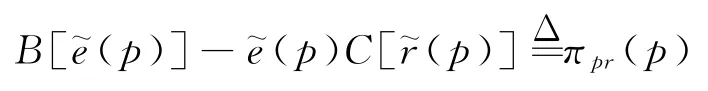
證明當p≤C'(0)時,結合式(3)、(4)可得:
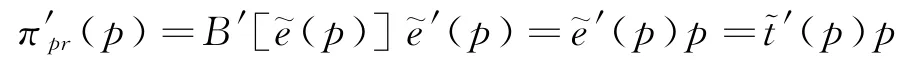
當p>C'(0)時,結合式(3)~(5)可得:
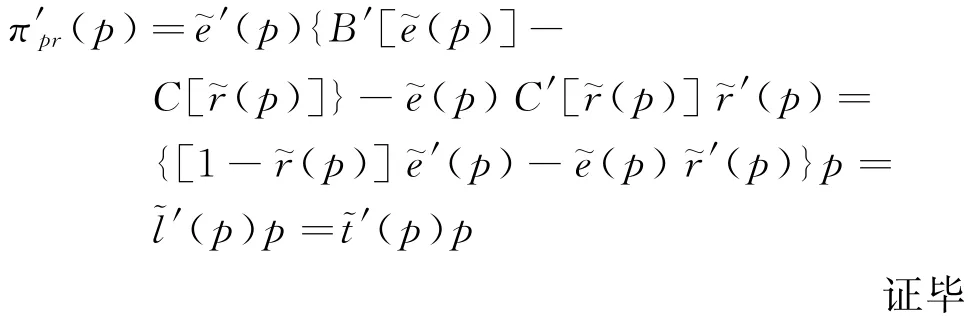
2.2 面向排污權市場價格不確定情境的基本模型
作為價格接受者的企業,盡管無法對排污權市場價格做出完美預測,但是在實踐中可以根據對排污權交易的歷史價格、經濟發展走勢等的分析,形成對未來排污權市場價格的預判。
因此,記x∈[0,∞)為企業生產計劃制定時對排污權市場價格的預期值,結合式(1)與命題1 可知,在排污權市場價格不確定情境下,企業凈收益函數可進一步表述為
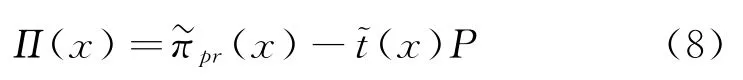
由此也可將模型式(2)所述特定p下的決策優化問題轉化為排污權市場價格預期的最優選擇問題:
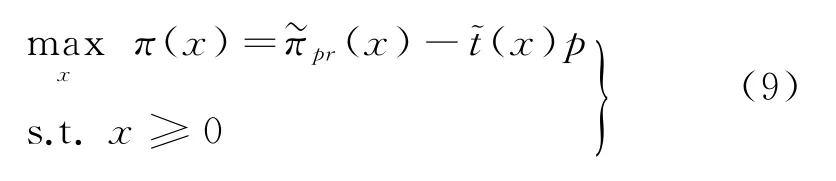
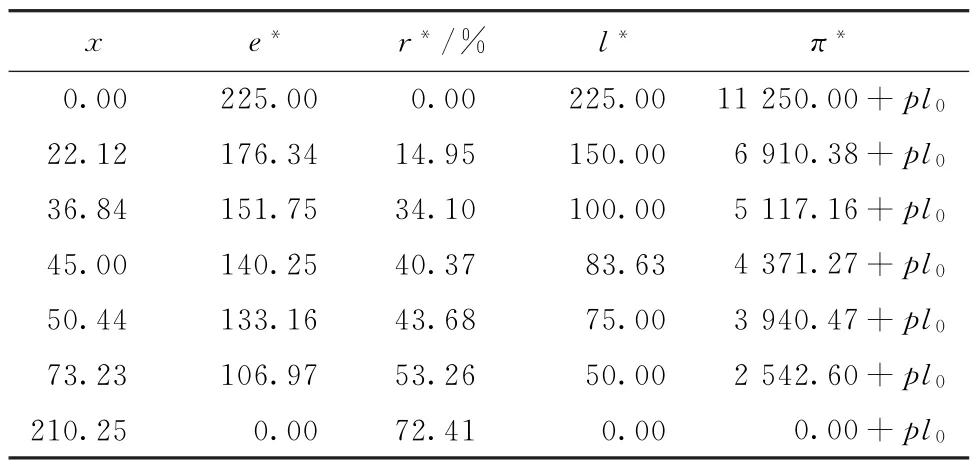
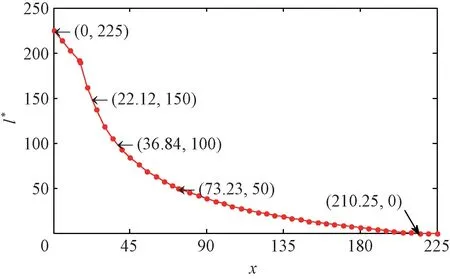
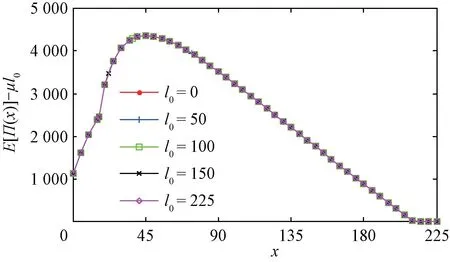
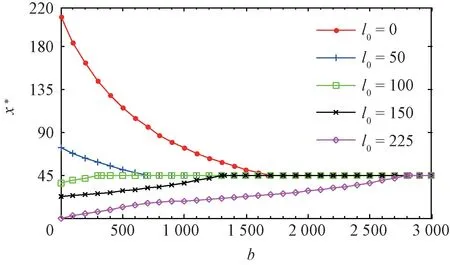
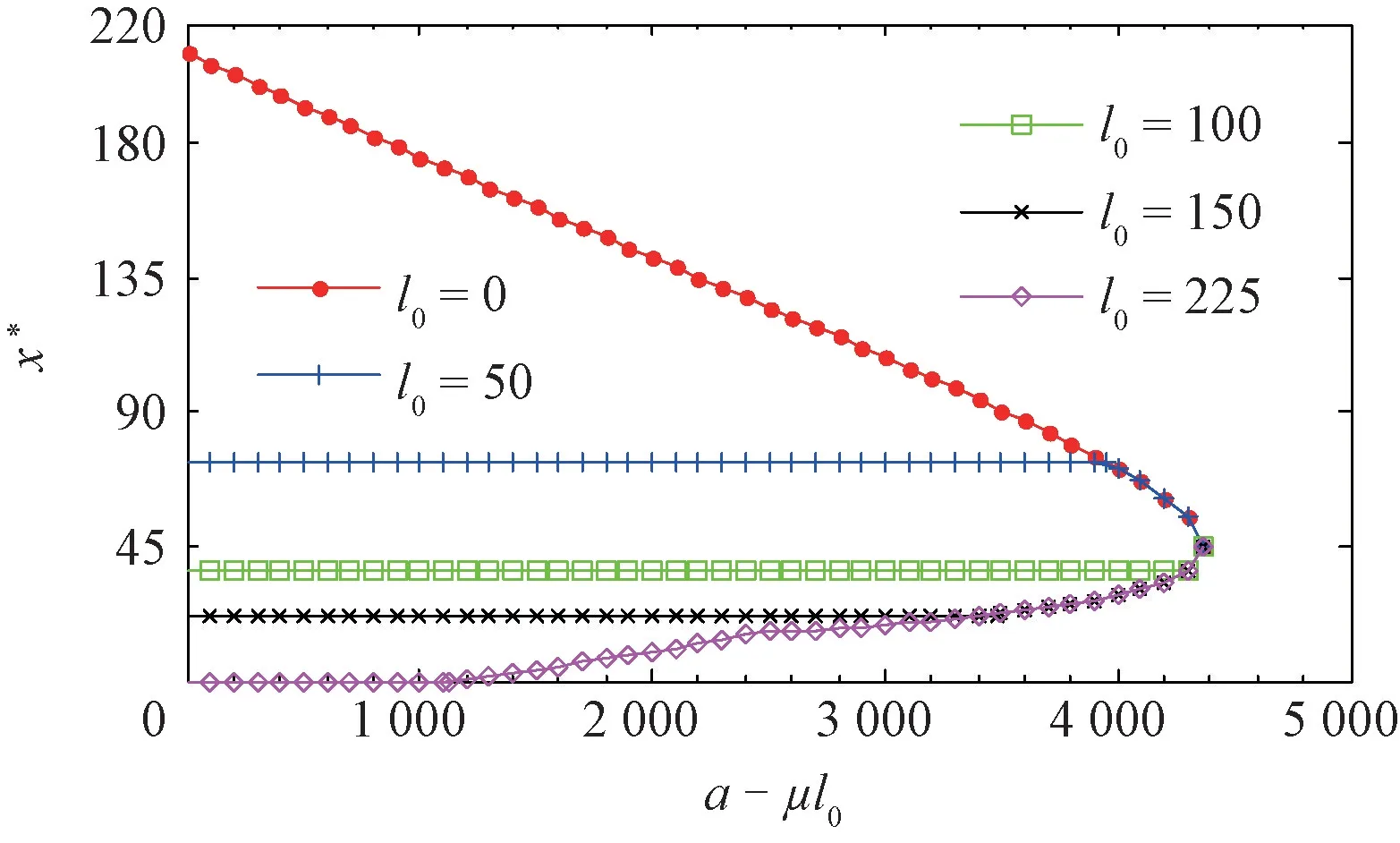
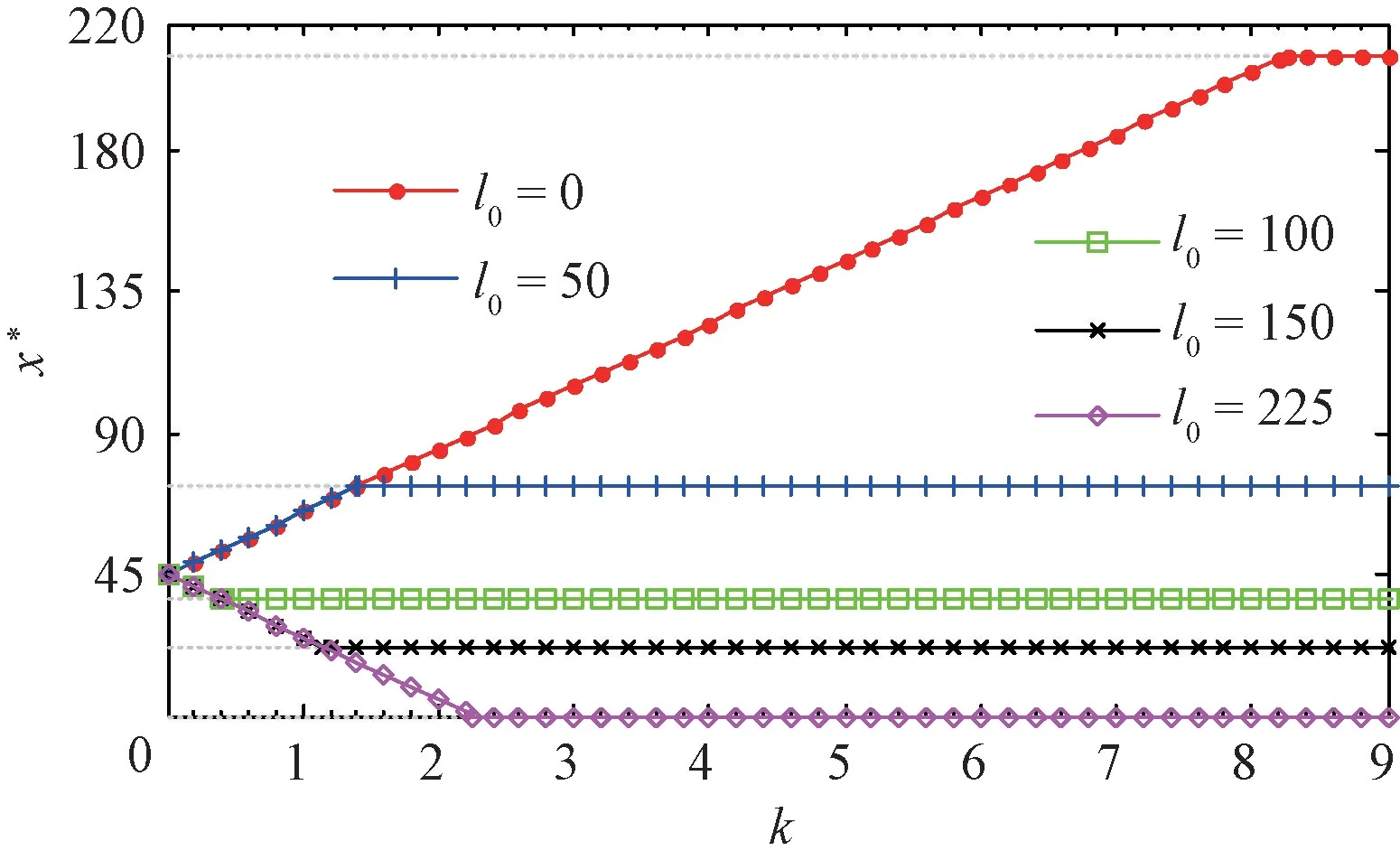
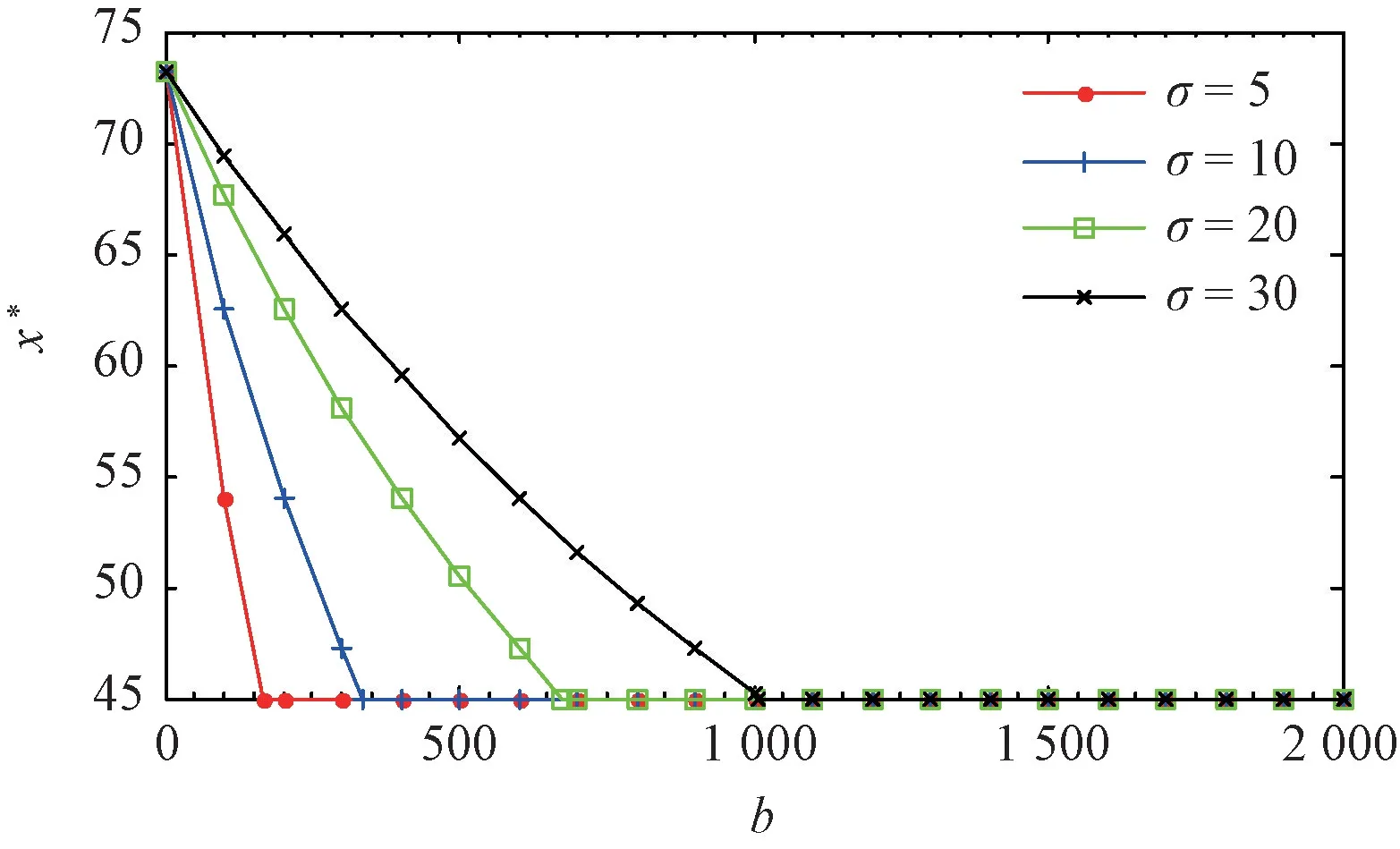
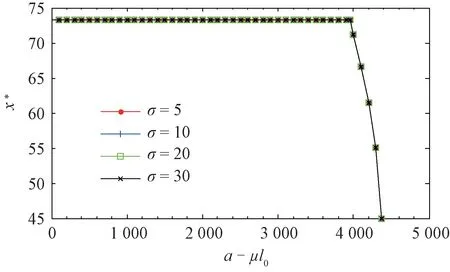
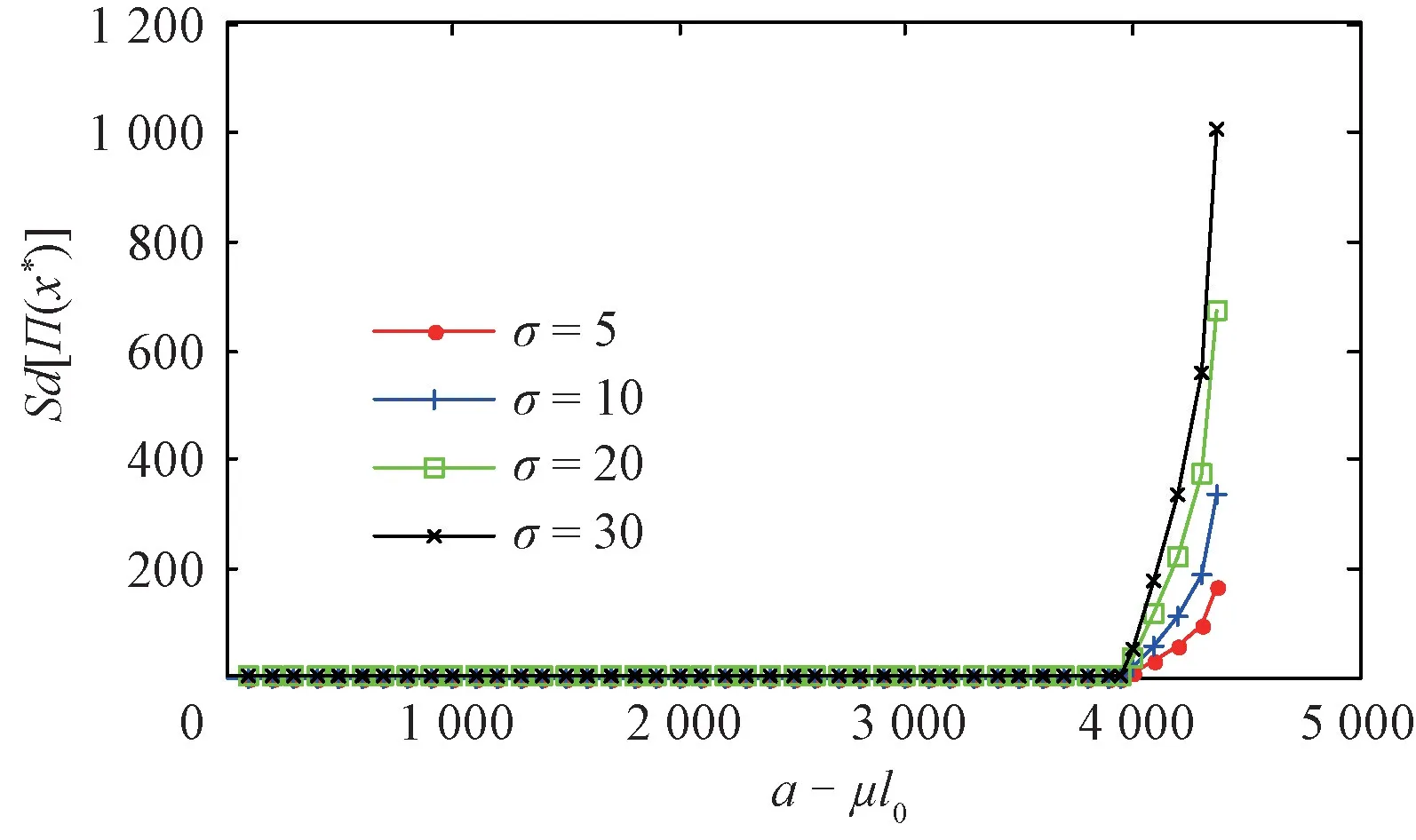
命題2任意特定排污權市場價格p下,π(x)關于決策變量x∈[0,∞)連續可微。其中:當p 當p≥pmax時, 進而,基于命題1所述價格追隨者的最優生產策略,模型式(9)的最優解為 證明因與在[0,∞)上連續可微,易得π(x)在[0,∞)內連續可微,且π'(x)=~t'(x)(x-p)。當p≥pmax時,若x≥pmax,由命題1知, 故π'(x)=0;若x 由式(8)與命題2易見,企業面對排污權市場價格不確定性的決策困境。一般而言,僅當x=P時,決策是最優化的,而不論是高估或低估未來排污權市場價格都會導致不同程度的利潤損失。 進一步,由式(8)可以計算得到企業隨機利潤的均值與方差,分別為: 由式(13)、(14),結合命題2易得: 命題3排污權價格不確定情境下,企業隨機利潤的期望值函數E[Π(x)]關于x∈[0,∞)連續可微,且有:①當μ 此外,E[Π(x)]在內單調遞增;當μ 命題4在排污權價格不確定情境下,企業隨機利潤的方差函數V[Π(x)]同樣關于x∈[0,∞)連續可微,且有 相應地,V[Π(x)]的值域為且僅當x=時,V[Π(x)]=0。換言之,實現隨機利潤方差最小化的最優決策為且 均值-方差模型是Markowitz[21]提出的風險投資分析工具。其核心思想在于:通過用均值和方差來刻畫收益和風險,在“高收益”與“低風險”兩大相互制約的決策目標之間做出最佳權衡。 顯然,最理想的決策方案是能夠在風險全局最低時獲得全局最大的預期收益。然而,由命題3、4易知,該理想結果僅在這一特例情況下存在,因此,決策者一般需依據特定決策偏好對這兩大目標進行權衡,選擇相對滿意的有效解。 為了系統刻畫排污權價格不確定情境下的企業生產決策,遵循均值-方差模型的分析框架,建立下述3種基于不同典型決策偏好的決策模型: 在可接受利潤標準差波動范圍,即風險容忍水平b≥0內,實現預期利潤最大化(P1): 在滿足最低預期利潤目標a的基礎上,實現利潤波動風險最小化(P2): 特定風險厭惡系數k下,實現綜合考慮均值與方差的期望效用值最大化(P3): 需要說明的是,因排污權具有緊缺性,企業初始配額通常不會過量,故重點分析l0≤的情形。 為了深入考察排污權價格不確定情境下的決策行為特征、驗證所得結論,參照文獻[3,19-20],細化假設如下: 假設4單位產量的產污量為ε,并考慮線性逆需求函數pc(q)=κ -αq,進而,B(e)=。此外,單位污染削減成本函數[3]C(r)=c0r/(1-r)。 設定企業相關參數基礎值為:κ=150,α=0.5,ε=1.5,c0=16。由此可得:pmax=210.25=225,不同排污權市場價格x下的企業最優決策結果如表1所示,并與命題1及其性質所述一致:e*、l*和π*與x負相關,r*則與x正相關。其中,排污權最優持有量l*與x之間的關系如圖2所示。 表1 基礎參數取值下的企業最優決策結果 圖2 排污權最優持有量l*與x 之間的關系 進而,由t*=l*-l0可知,企業參數確定時僅取決于l0,即為l*=l0時所對應的排污權價格,特殊地,當l0=0時=pmax=210.25,而且隨著l0從0不斷增加將從pmax逐步降低,直至l0=時=0。不失一般性,設定排污權市場價格參數取值為:μ=45,σ=20。 由E[Π(x)]=可知,E[Π(x)]取決于兩個外部變量:l0與μ。值得一提的是,就特定企業而言,當x確定時與均確定,與l0、μ、σ等無關則只受l0的影響。 圖3所示描述了既定排污權價格隨機場景下期望利潤E[Π(x)]隨排污權預期價格x的變化趨勢,圖4所示以l0=50為例刻畫了μ變動對E[Π(x)]的影響。 圖3 不同l0 下企業期望利潤E[Π(x)]的變化趨勢 圖4 不同μ 下E[Π(x)]的變化趨勢(l0=50) 由圖3、4可見:①不同l0下,E[Π(x)]的差異在于初始配額的期望價值μl0;②μ變動對E[Π(x)]的影響體現在改變了預期交易排污權的期望成本,進而,因為=0,所以當l0確定時,E[Π(x)]在x=處不會因μ的變動而發生變化;③無論l0或μ取值如何,E[Π(x)]在x=μ處達到最大值,即。同理,由V[Π(x)]=Sd2[Π(x)]=(x)σ2可知,隨機利潤的方差與標準差取決于外部變量l0與σ,而與μ無關。 由圖5 可見,無論l0取值如何,Sd[Π(x)]在處最小且為0,而且x與的偏離越大,隨機利潤的不確定性也將增加,進而實現方差(標準差)最小化的最優決策為 圖5 不同l0 下Sd[Π(x)]的變化趨勢 圖6所示進一步反映了不同l0下隨機利潤的期望與標準差之間的對應關系,即有效前沿曲線。 圖6 不同l0 下的有效前沿曲線 其中,任意l0下,E[Π(x)]-μl0取值為1 125、4 371.27和0處分別對應x=0,x=μ,x≥pmax時的狀態。當x=時,顯然與Sd[Π(x)]=0處相對應。 此外,當l0既定時,σ變動會等比例改變特定x下的Sd[Π(x)],如圖7所示。換言之,排污權價格不確定性越高,則隨機利潤波動性也將越大。 圖7 不同σ 下Sd[Π(x)]的變化趨勢(l0=50) 圖8~10 分別展現了基準情景下基于模型(P1)~(P3)的企業最優決策變化趨勢。值得一提的是,由表1可知,當μ=45時,期望效用最大化的最優決策結果為:若l0<83.63,購買排污權;若l0>83.63,則出售排污權。 由圖8 并結合圖6 可見:①與命題5 所述一致,當b=0時,無論l0如何,即極度風險厭惡的企業不會選擇交易排污權。隨著b的不斷增加,企業風險容忍度也不斷增加,對于期望最優決策下需要購買排污權的企業而言將逐步降低,與之相應的是,企業將擴大生產、降低污染削減水平,并增加排污權購買量。對于期望最優決策下需要出售排污權的企業而言則將逐步提高,即降低生產規模、提高污染削減水平,以降低其排污權占用量,進而其排污權出售量也將隨之提高,直至b≥Sd[Π(μ)]時=μ。② 因為μ既定時,也確定,所以由Sd[Π(μ)]=可知(見圖8),企業初始配額l0越接近期望最優決策下的排污權占用量,則排污權市場價格不確定性給企業帶來的決策風險越小,進而與期望最優決策的偏離越小,且企業將在更小的風險容忍度b閾值上采用期望最優決策。 圖8 不同l0 下的模型(P1)最優解 由圖9 并結合圖6 可見:①與命題6 所述一致,當a≤E時,即不交易排污權時的期望利潤已經能使企業滿足是風險最小的理性選擇。隨著a的增加,當a>E時,無論l0如何都將趨于μ,直至a=E[Π(μ)]=4 371.27+45l0時=μ;而當a>E[Π(μ)]時,期望利潤水平無法得到滿足,故不存在最優解。②l0越接近風險中性最優決策下的排污權占用量~l(μ),企業將在更高的期望利潤水平a內傾向于不參與排污權交易,以規避排污權市場價格不確定性帶來的決策風險。盡管如此與風險中性決策之間的偏離卻也越小。 圖9 不同l0 下的模型(P2)最優解 圖10所示則較好地支持了命題7:①當k=0時,利潤風險不會給企業帶來影響=μ。隨著k的增加,利潤風險考慮占綜合效用的比重越來越大,進而產生最優決策與風險中性最優決策的偏離,企業愈發趨向于不參與排污權交易,直至kσ≥時,不交易排污權的利潤風險已經為0,進而k增加不會再對企業決策產生影響。②由kσ≥并結合表1可知,同樣有:l0越接近~l(μ),風險規避的企業將在更小的風險權重k內轉向不參與排污權交易,且與風險中性決策之間的偏離卻也越小。 圖10 不同l0 下模型(P3)最優解 進一步,以l0=50為例開展σ變動對最優決策影響的敏感性分析(見圖11~13)。由前已知,當l0=50時=73.23,風險中性最優決策結果為購買排污權,且σ變動只會等比例改變特定x下的Sd[Π(x)],而不會影響E[Π(x)]。 圖11 不同σ 下模型(P1)最優解 圖12 不同σ 下模型(P2)最優解 圖13 不同σ 下模型(P3)最優解 模擬結果同樣較好地支持了所得結論,并表明:①對于模型(P1),σ越大,當=μ時,企業的最低風險容忍度b將等比例增加,且在相同b下,σ越大,則與風險中性決策的偏離有擴大的趨勢。②對于模型(P2),σ變動不會影響企業期望利潤,進而也不會改變企業對排污權市場價格的最優預期,即不同σ下隨期望利潤水平a變動的變化趨勢完全相同。但是,當a∈ (EE[Π(μ)]]時,σ越大,則最優解處的利潤波動風險越大,如圖14所示。③對于模型(P3),因在相同風險權重k下σ越大,則利潤風險的影響將越明顯,進而σ越大,則企業風險規避特征也將顯著,即相同k下,其對排污權的最優價格預期越趨于 圖14 不同σ 下P2最優解處Sd[Π(x*)]的變化趨勢 通過考察作為價格追隨者的理性企業在排污權交易管制下的最優行為反應,將排污權價格不確定情境下的生產決策優化問題轉化為排污權價格預期的最優選擇問題。據此,基于均值-方差模型的分析框架,深入探討了排污權價格不確定所引致的企業生產決策風險測度以及考慮風險的決策優化問題。結果表明:企業不參與排污權市場交易時所面臨的利潤波動風險最小且為零風險;相應地,盡管基于不同決策偏好所形成的最優決策也不盡相同,但是考慮隨機利潤風險的最優決策均將系統性偏離風險中性最優決策,而且企業風險規避程度越高,則越趨于不參與排污權交易。該結論也較好地從微觀行為選擇層面解釋與揭示我國排污權交易市場中普遍存在的“惜買”與“惜賣”現象的發生機理。同時,研究結果也從側面印證了引導企業樹立合理的風險意識、排污權初始分配兼顧企業實際需求等的重要性與必要性,特別是宜將如何有效降低價格不確定性、建立相對穩定的排污權市場價格形成機制作為體系構建與完善的重中之重。 此外,結合我國排污權交易的實施特點,未來可從納入排污權多期有效與有償分配等情景要素以及考慮企業多期決策問題等方面進行拓展研究。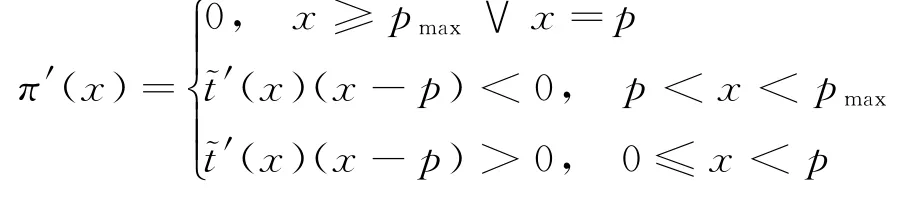
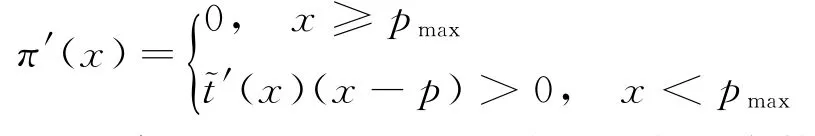
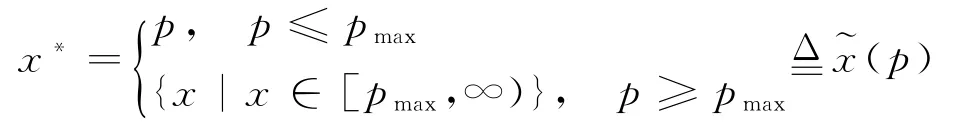
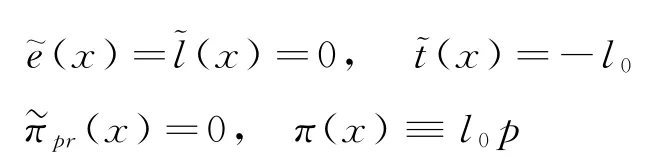
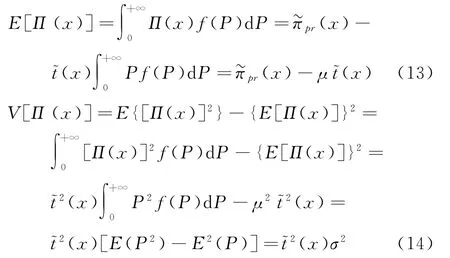
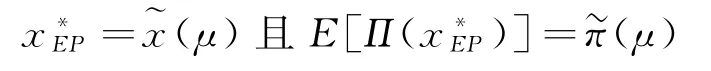
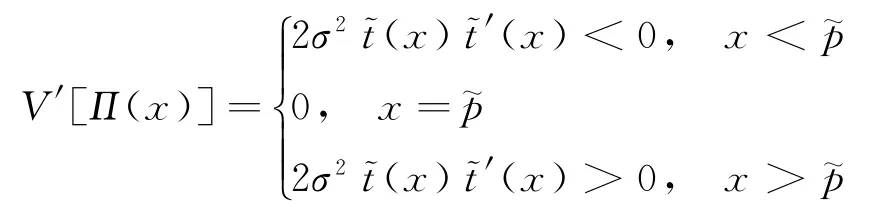
3 基于均值-方差模型的決策分析
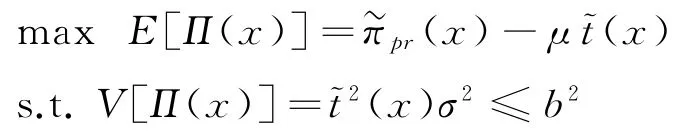
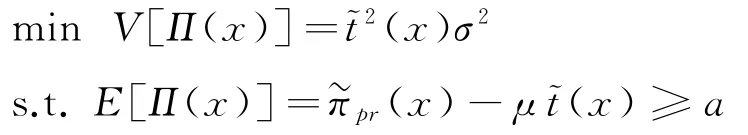
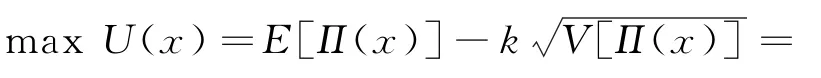
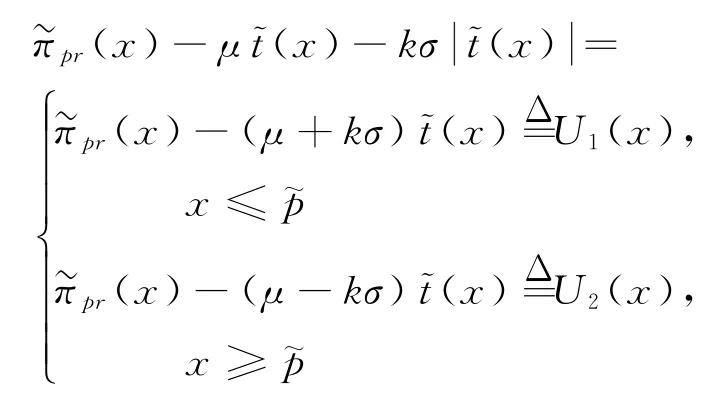



4 算例分析
4.1 企業隨機利潤的期望與方差
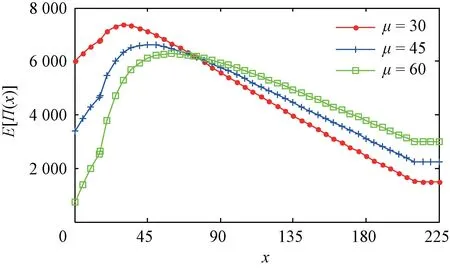
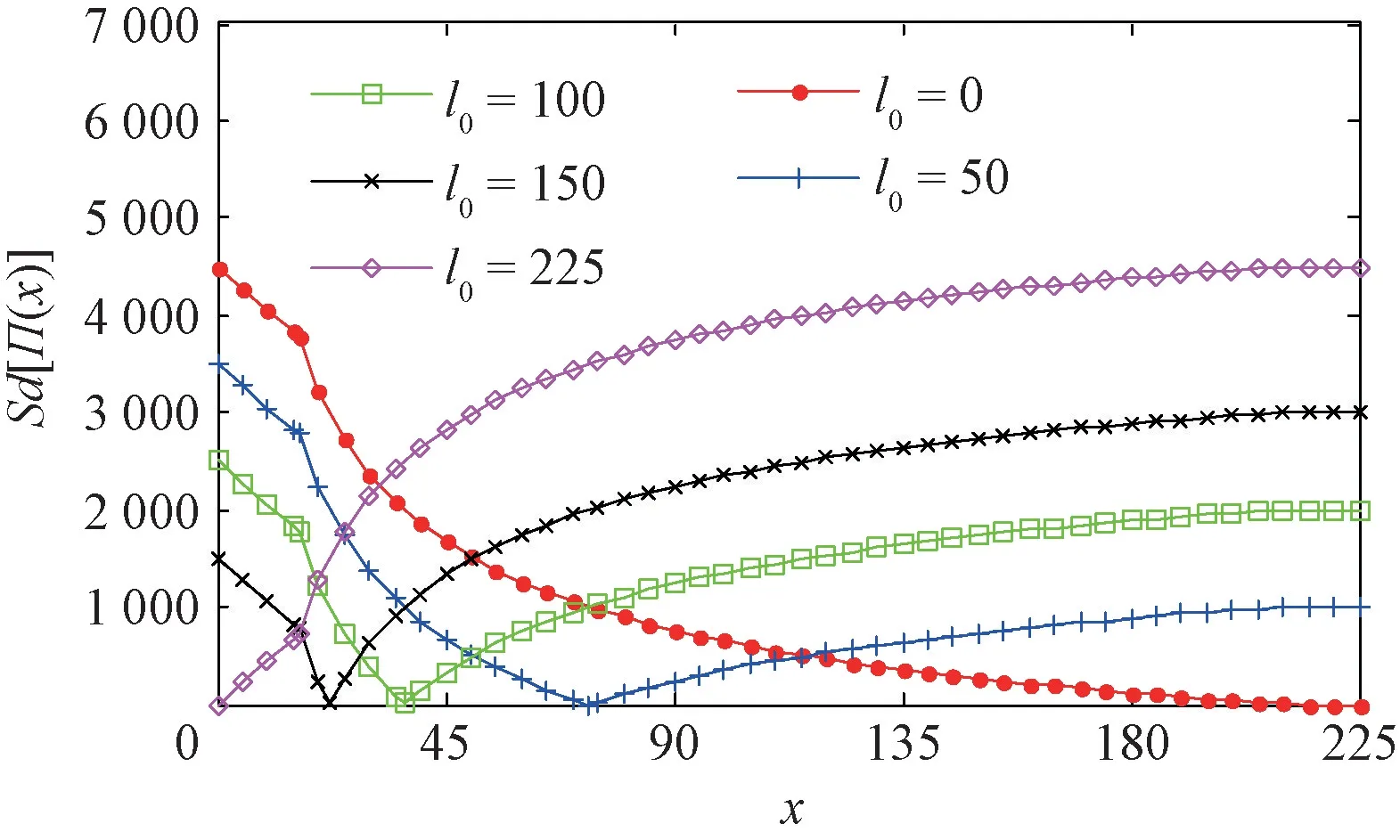
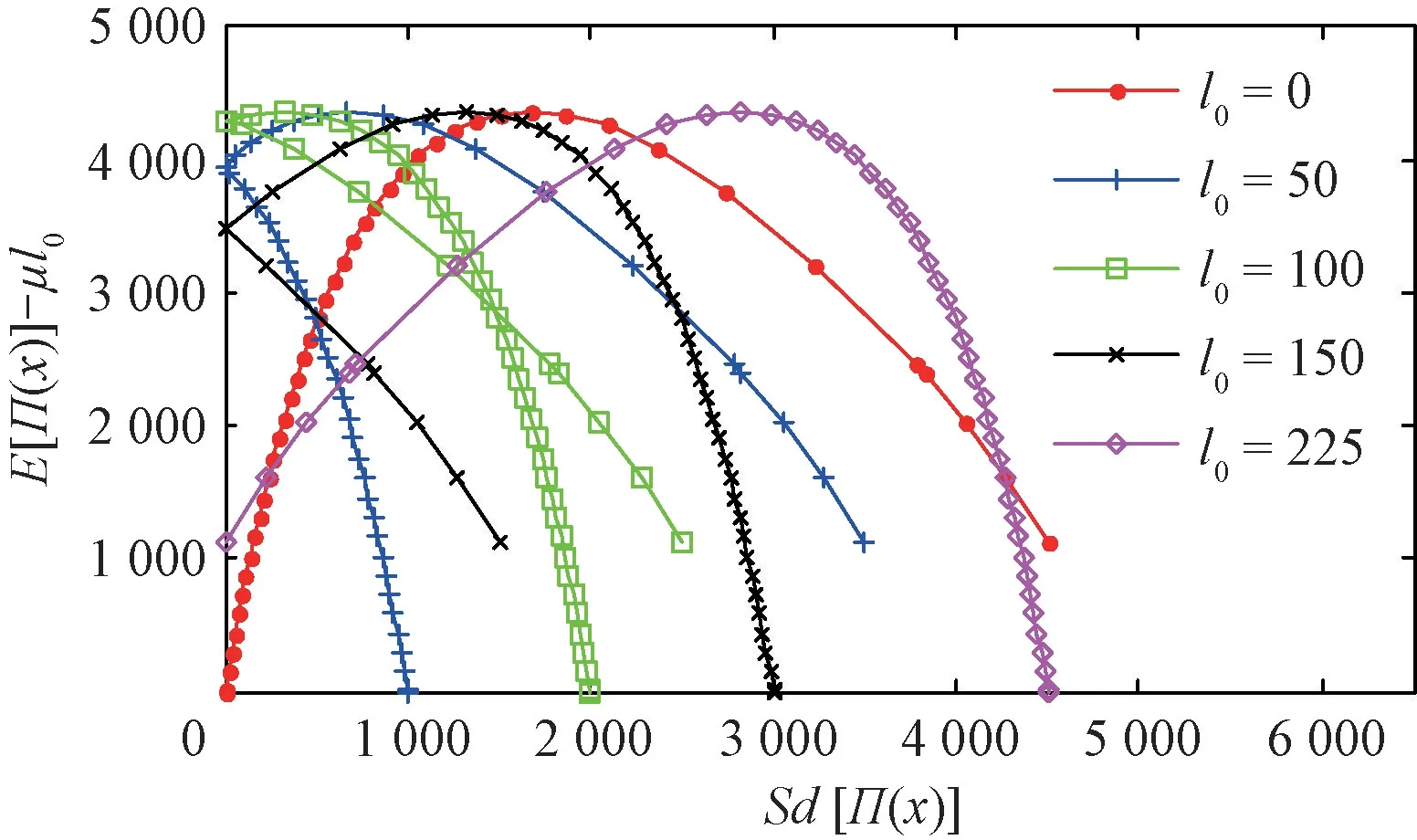
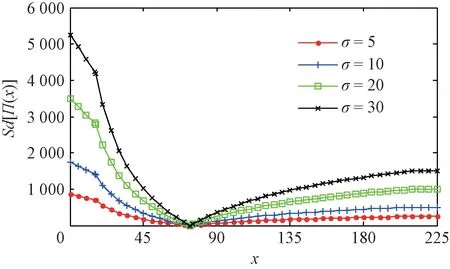
4.2 基于均值-方差模型的優化決策

5 結語

