基于多維運籌函數的城市軌道交通網絡優(yōu)化設計

商 闊

（山東大學 數學學院，山東 濟南 250100）

依據交通運輸部的數據，截至2020年12月31日，全國已經有44個城市開通了城市軌道交通，一共擁有233條交通線路，總長度達到7545公里，地鐵車站4600多座，在軌運行的車輛達到2528輛。建成后交通網絡將更加復雜①。

從數據上來看，城市軌道交通客流量很大，其中乘客出行目的地復雜，具有很大的不確定性。研究城市軌道交通主要是依據O-D數據，O-D數據是一種從起點到終點之間的數據，這個數據可以通過調查得出，目前大多采用向路人采訪、或者是貨流的調查等等，依據這些調查數據，可以整理出不同的影響因素與起終點相關的各種分布研究，也可以做交通統計調查、交通發(fā)生的統計等圖直觀地描述交通狀況。

在現實中，可以利用城市的某時刻乘客O-D數據，并依據城市軌道交通的基礎信息數據、該時段的列車運行數據以及北京城市軌道交通的主要狀況，就可以從微觀領域涉及分析某個人最優(yōu)化的出行策略，并利用MATLAB軟件設計一套算法，盡可能地優(yōu)化乘客出行的最優(yōu)路徑安排。

1 已有的文獻

交通優(yōu)化是一個數學建模問題，數學模型是利用數學符號、數學理論、程序以及圖形等，對實際問題的本質進行高度抽象刻畫的一種模擬方法。從知識體系來看，高等數學分為數學原理的基礎研究、數值的計算以及進行數學建模，數學建模是數學知識在實踐中運用的重要體現，在軟件方面，如MATLAB、Mathematica等軟件的開發(fā)，更是推進了數學的發(fā)展，在新工科建設的背景下，數學建模也是重要的課程。

陳文斌等[1]從單點信號控制出發(fā)，考慮到一些交叉口軌道交通運行的特點，針對信號相位組合提出優(yōu)化策略，通過定義相位燈中的綠燈利用率，把相位燈中與交通流組合的問題抽象為交通對象的聚類問題，然后綜合運用聚類分析，建立優(yōu)化模型，模型將軌道交通在交叉口的延誤時間作為優(yōu)化對象，并運用vissim進行仿真，得出這樣可以使得總延誤時間降低15%左右。朱宇婷等[2]在深入考察軌道交通擁擠和客流的脈沖特征之后，用線路中各個發(fā)車的時刻相位作為變量，以乘客支出最小化為目標，以軌道交通的容量、間隔、站臺最大容量和補貼等為約束條件，基于遺傳算法等技術，提出了調整軌道交通費用和旅客出行開支的優(yōu)化方法。萬浩純等[3]將旅行乘客的最短出現時間與客流量進行了匹配，在考察了停站次數、線路車輛以及調查的時間間隔等因素的前提下，通過蟻群和遺傳算法求解了兩個目標同時實現的可能性，提出了越行判別的方法，建立了優(yōu)化模型，并以上海的16號軌道交通為例，進行了驗證，結果表明，優(yōu)化后乘客消耗的時間降低了9.2%，驗證了模型的有效性。郝雪、王世平[4]分析了軌道交通中的供電問題，試圖將弓網系統進行優(yōu)化，主要是采用提高弓網耦合建立模型仿真的精度，對傳統模型中較難實現受電弓滑板的情況描述問題進行了改進建模，并針對弓網系統中振動和剛性接觸的截面導致仿真不準確的問題，提出利用接觸壓力來檢測的原理，并運用Ansys軟件進行了建模仿真，結果顯示，仿真結果比傳統檢測提高了精度，具有更高的可靠性和精確性。郭曉林[5]綜合考慮的交通中的三大效益，即經濟效益、交通效益和社會效益，提出了交通最優(yōu)化的軌道綜合模型，并以寶雞市的交通作為樣本，驗證了模型的可靠性。劉洪麗、馮伯林[6]運用矩陣迭代的方法進行了道路優(yōu)化的建模，通過與Dijkstra算法進行對比發(fā)現，該算法可以更加簡潔地進行優(yōu)化，顯示出所走的路徑，并利用某個中等城市的數據進行了分析。

上述文獻采用的方式都是先數學建模，然后再進行樣本的驗證，從文獻上看，數學建模的思想是重要的，首先有了建模優(yōu)化的思路，問題也就迎刃而解。下面先利用運籌學中的一些知識構建出建模思想，然后利用MATLAB進行模型化，最后用樣本進行驗證。

2 最優(yōu)交通設計的思路

2.1 繪制出行距離分布圖

乘客的出行距離分布，主要是采用graph函數，將距離為1（即相隔一站距離）的車站和換乘車站相連，建立一個擬地鐵線路圖。然后利用distances函數，求出每一個乘客的起點和終點的最短距離，即為出行距離。但注意到換乘車站雖然相連但距離為0，故給予所有因換乘相連的車站以權重0.01，這樣在計算最短距離時，換乘車站不會有干擾（只有在換乘超過100次時才會有影響，但實際這種情況不會發(fā)生），這樣以1為一個距離段，去除極少數變量后，利用distances函數繪制出行距離分布圖。

2.2 任意兩站的最短路徑設計

利用shortestpath函數求出每個人走最短路徑需依次乘坐的車，然后根據每個人的入站時間和列車的到達、出發(fā)時間，第一輛車的出發(fā)時間需在乘客入站時間之后，第二輛車的出發(fā)時間需在上一輛車到達換乘點的時間之后，以此類推，找出符合條件的列車的編號。最后用shortestpath函數可以求出任意兩站的最短路徑。

2.3 運用樣本進行檢驗

程序是否可靠需要樣本的檢驗，這里采用北京軌道交通某一時段的具體數據，帶入程序進行驗證，并針對結果進行評析。

3 最優(yōu)交通設計的MATLAB代碼

3.1 程序的設計

按照以上思路，利用MATLAB可以設計出最優(yōu)交通路線：

load（'origin.mat'）//number=table2array（OD（：，1））;//originator=table2array（OD（：，2））;//destination=table2array（OD（：，3））;//start_time=table2array（OD（：，4））;//f inish_time=table2array（OD（：，5））;

%以上操作可以將O-D數據表格數據分為五個相應變量

l=1：328;//k=1;//whilek<=length（originator）//if~ismember（originator（k），l）//~ismember（destination（k），l）//number（k）=[];//originator（k）=[];//destination（k）=[];//start_time（k）=[];//finish_time（k）=[];//end//k=k+1;//end//duration=finish_time-start_time;

clear lk%去除所有非法變量

station_number=table2array（information1（：，1））;//station_name=table2array（information1（：，2））;//line=table2array（information1（：，3））;//road=zeros（328）;

for k=1：328//for l=1：328//ifstation_name（k）==station_name（l）//road（k，l）=1;//else

if abs（k-l）==1&&line（k）==line（l）//road（k，l）=1;//else//road（k，l）=0;//end//end//end//end%根據所給地鐵路線圖，生成一個“道路”矩陣

road（37，54）=1;//road（54，37）=1;//road（193，237）=1;//road（237，193）=1;//road（300，150）=1;

road（150，300）=1;%環(huán)形線特殊情況

clearlk;//G=graph（road，'omitselfloops'）;//for k=1：height（G.Edges）

if station_name（G.Edges.EndNodes（k，1））==station_name（G.Edges.EndNodes（k，2））

圖1 北京市部分乘客出行距離分布圖

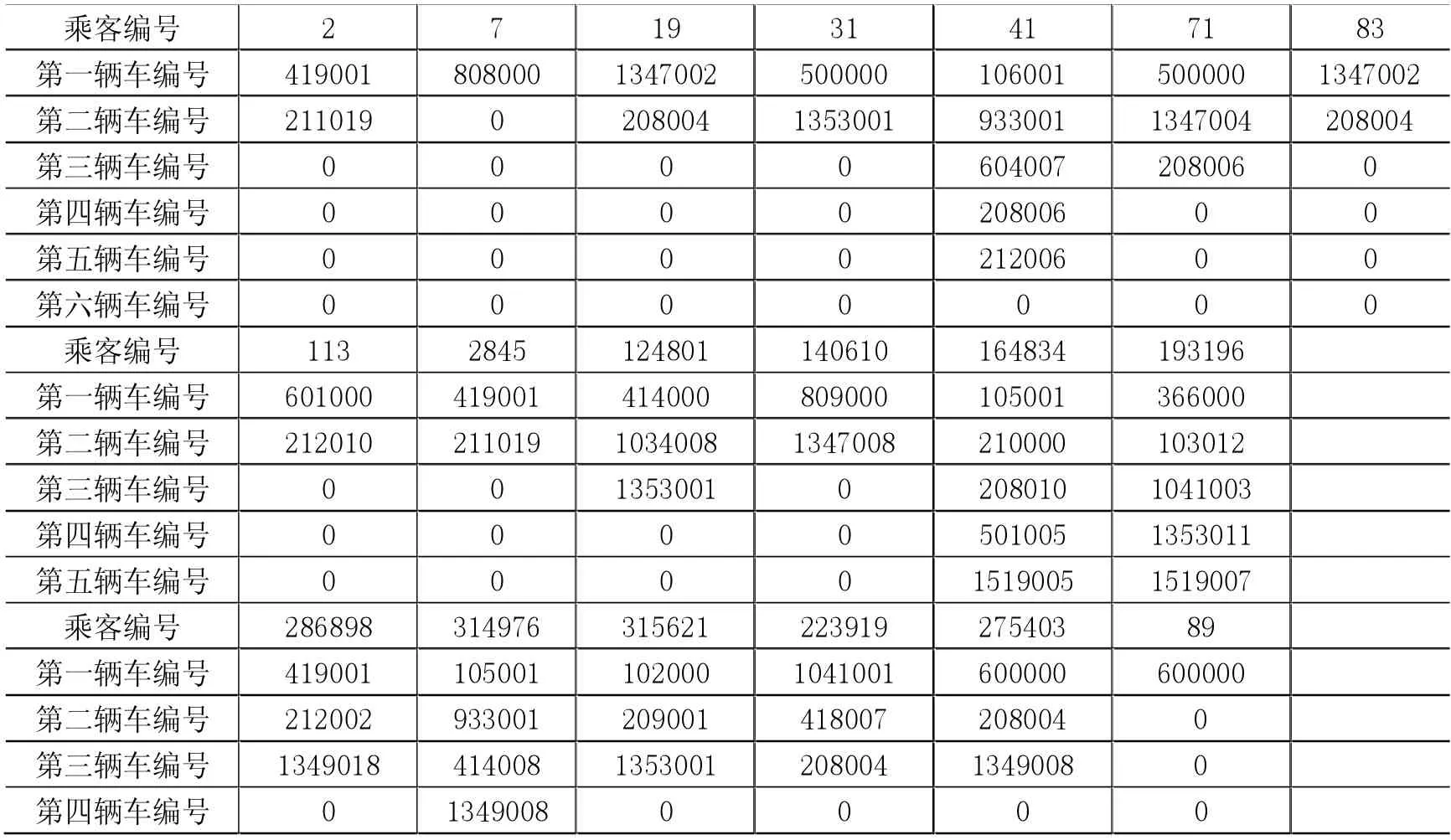
表1 北京市某時間段乘客的最優(yōu)乘車路線設計

G.Edges.Weight（k）=0.01;//end//end//for k=1：length（originator）

distance（k，1）=distances（G，originator（k），destination（k））;//end//distance=floor（distance）;

clearlk;//%統計所有人的出行距離

c=0;//m=-1;//while sum（c）<10^4//m=m+1;//c=distance<=m+1;//c=distance（c）>m;//end

st=m;//%篩選出最小的滿足運行量在圖像上明顯的時段

while sum（c）>=10^4//m=m+1;//c=distance<=m+1;//c=distance（c）>m;//end//ed=m+1;

%篩選出最大的滿足運行量在圖像上明顯的時段

bin_dt=st：ed;//histogram（distance，bin_dt）;%繪制出行距離分布圖

clear bin_stcdedmnstsupposed_todaybin_edbin_dubin_dt

subways（end+1，：）=subways（1，：）;

x=[2，7，19，31，41，71，83，89，113，2845，124801，140610，164834，193196，223919，275403，286898，314976，315621];//x=string（x）;//subways_taken=[];//for n=1：length（x）

line_number=find（number==x（n））;//P=shortestpath（G，originator（line_number），destination（line_number））;//now=start_time（line_number）;//p=1;//while length（P）>1

l=find（subways.station==P（1））;//l=l（subways.station（l+1）==P（2））;//l=l（subways.set_off（l）>now）;//mintime=min（subways.set_off（l））//l=l（subways.set_off（l）==mintime）//l=l（1）;l=subways.number（l）;//subways_taken（p，n）=l;//p=p+1;

l=find（subways.number==l）;//l=l（subways.set_off（l）>now）;//A=subways.arrive（l）;//l=subways.station（l）;//while l（1）~=P（1）&&l（2）~=P（2）//l（1）=[];//A（1）=[];//end//k=0;//while l（1）==P（1）

l（1）=[];//P（1）=[];//k=k+1;//ifisempty（P）||isempty（l）//break//end//end//now=A（k）;//end//end

clearklmintimeAnansline_numbernowpPx//subays_taken;//P=shortestpath（G，a，b）;%對于需要從a站到b站的乘客，輸入左邊相應的程序即可得到最短路徑。

3.2 程序執(zhí)行

為了驗證程序有效性，輸入北京市的有關數據，然后執(zhí)行上述程序后，得到所有人出行（默認所有人按最短路徑）距離分布見圖1。

帶入相關的數據，可以解出最優(yōu)出行路線設計。如表1所示。

從結果來看，本程序可以對乘客的路線進行優(yōu)化，并能夠節(jié)約出行時間，同時也可以防止軌道交通的過度擁擠，最大化地利用軌道交通。

4 結論

出行的最優(yōu)設計有利于提高交通運行的效率，減少不必要的轉車，降低軌道交通的擁擠程度。本文利用運籌學的相關函數，設計了MATLAB程序，并以北京市為例進行驗證，從效果來看，程序運行良好，能夠得到期望的效果。

注釋：

①交通部《2020年城市軌道交通運營數據》，2021年4月3日交通要聞。