社會網絡問題中的算法

李曉明

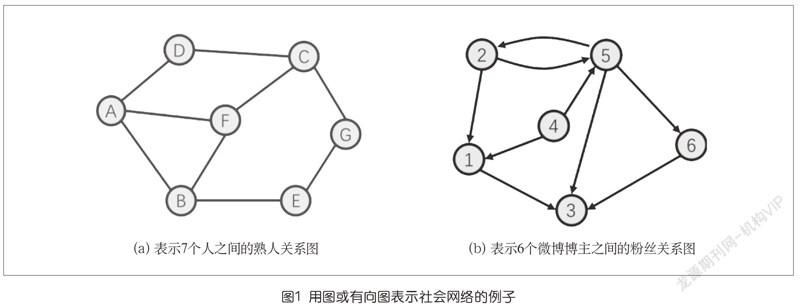
人和人之間的關系，可以看成是一個網絡，可以用圖或有向圖來描述，或者說用它們來建模。在本欄目第2期討論一筆畫問題時我們接觸過圖，在第4期談連通問題時針對的也是圖，而在第13期討論網絡最大流問題時采用的模型則是有向圖。第21期談選舉，也用到了有向圖。圖和有向圖是用算法求解問題中十分常見的一類模型。

取決于所考慮的人群范圍和關系的定義，社會網絡，有時也稱社交網絡，可以多種多樣。最熟悉的，是現實生活中的“熟人”關系，見面相互都能叫得上名字，用圖來描述就很合適，如圖1（a）所示。而微博博主之間的“粉絲關系”，不一定是互相的，用圖來表示就不合適了，需要用有向圖，如圖1（b）所示。箭頭方向就表達了粉絲關系的單向性。如果兩個人互粉，如節點2和節點5，那么他們之間就有兩條不同方向的邊。

社會網絡分析有許多現實的意義。例如，在新冠肺炎疫情期間，發現一個病例，要確定他有哪些“密接者”，就涉及社會網絡分析。那種社會網絡，其中的邊具有時間特性（只是在某個時間段存在），也稱作“接觸網絡”。現在一些城市要求市民在一些場所通過掃描特定的二維碼“打卡”，其意義之一就是為了在發現病例的時候，能夠迅速構建與他相關的接觸網絡。

本文介紹社會網絡分析中的兩個基礎算法，讓讀者從中了解社會網絡分析的一種主要計算模式——矩陣運算①。這類算法，從算法邏輯的角度來說，會顯得比本專欄前面介紹過的那些算法簡單許多，它們的引人入勝之處在于其結果體現了某些社會現實意義。在討論中，我們總假定網絡結構是已經給定的有向圖，而且采用的是鄰接矩陣表示。在本欄目第4期討論圖的連通問題時，我們用過圖的鄰接矩陣表示。不過那里僅涉及無向圖，鄰接矩陣是對稱的;本文則主要關注有向圖，鄰接矩陣一般不對稱。例如，圖2（a）就是前面圖1（b）中有向圖的鄰接矩陣表示，其中行和列的編號對應圖中的節點，即第i行第j列的值aij=1，當且僅當有一條從節點i指向節點j的邊。有時候，如果需要表示一個節點指向自己的情形，就會有aii=1。

對矩陣概念陌生但對編程比較熟悉的讀者，不妨就想像程序語言中的“二維數組”。在Python中可用二維列表或者numpy中的數組直接體現，如圖2（a）中的矩陣用二維列表給出就是：

A=[[0，0，1，0，0，0]，

[1，0，1，1，1，0]，

[0，0，0，0，0，0]，

[1，0，0，0，1，0]，

[0，1，1，0，0，1]，

[0，0，1，0，0，0]]

用A[i][j]訪問它的第i行第j列元素。有時候，為方便起見，也用矩陣（數組）的第i個行向量和第j個列向量來分別指代A[i][j]，j=1，2，…，n和A[i][j]，i=1，2，…，n。注意，它們分別都包含n個元素，視覺形象上對應數組的行和列。

我們要討論的兩個算法，其社會現實意義分別與社會網絡中人們的“發言權”和“影響力”有關。為了體會這些說法的現實含義，不妨考慮下面這樣一種情境。

設想在某中學的一個班里，學生們相處久了相互已經比較熟悉。現在要討論某個話題，如生物多樣性，或者校門口那一棵大槐樹的高度。教師讓每個學生分別填寫表1，寫出自己的姓名和2～5個認為對該話題比較有發言權的同學的姓名。

教師收上來這些紙條，你馬上能意識到，她有了一個社會網絡的數據，而且其中表達的關系是有方向性的：每個學生是其中一個節點，如果學生i在他的表中提到了學生j的名字，那么網絡中就有一條從i指向j的邊。例如，圖3就是一次實際填報數據給出的結果。我們看到每個節點發出有若干指向其他節點的邊（稱為出向邊），同時作為結果，每個節點也“收到了”若干來自其他節點的邊。此處重點是，這種“入向邊的條數（稱為“入度”），不同節點很可能是不同的，反映了一個學生被其他學生“認可”的情況。

一般來說，針對一個話題，每個學生都會有自己的觀點，有的堅實，有的飄忽，姑且稱其為不同程度的“發言權”。而這種程度是被其他同學看在眼里，表達在上述表格中的。顯然，這種發言權意味著某種價值，有高低。我們來介紹一種評估這種價值的計算方法。

按照填表時給學生的背景意義，我們可以理解，如果節點i的入度大于節點j的入度，大致可以說明更多的人認為i比j對當下話題更有發言權。也就是說，節點的入度可以是發言權高低的一種指示器。不過我們還想更進一步，認為一個人的發言權不光取決于有多少人認為他有發言權，還取決于認為他有發言權的人有多大的發言權。同時，若某人認可的人較多，他的分量體現在一個人身上應該較少。直覺上，這是有道理的。利用一些合理的直覺（盡管不一定能證明總是對的），形成啟發式來指導計算，是利用計算機求解問題的一種基本策略。在本欄目前面的文章中我們已經看到過不少例子。在這種思想下，接著就要考慮兩點，一是將啟發式變成算法，二是在應用實踐中檢驗。

下面就是解決這個問題的著名的PageRank算法，它通過迭代同時更新每個節點的值，直到收斂誤差滿足要求或達到某個預設的迭代次數。算法要點是：在迭代的每一輪，讓每個節點將自己的當前值均分給出向鄰居節點，同時將從入向鄰居節點收到的當前值加和作為自己下一輪的當前值。圖4給出一個示意。關注左邊圖中的節點v，它有3個入向鄰居，每個有不同的出度。右邊則是按照上述算法思想對v進行更新的公式。

不難想到，基于有向圖中的連接關系，對每一個節點都可以寫出一個類似但不同的公式來。假設有n個節點，通常令每個節點的初值為1/n，按照公式進行迭代，就是PageRank計算的過程。在我們前面設置的背景問題下，這也就是學生們對某一個問題的“發言權”的計算過程了。

不過，上面只是闡述了“算法思想”。落實到明晰的算法描述還需要做些整理。關鍵在于“按不同的公式同時更新每個節點的值”具體怎么實施。這里首先要解決的是不同公式的統一表達問題。