不確定DoS攻擊下的異構(gòu)多智能體系統(tǒng)異步控制器設(shè)計(jì)

倪洪杰，俞文海，張 丹

(浙江工業(yè)大學(xué) 信息工程學(xué)院，杭州 310023)

由于多智能體系統(tǒng)理論在各種工程領(lǐng)域中具有巨大的實(shí)際應(yīng)用價(jià)值，近年來多智能體系統(tǒng)的分布式協(xié)同控制問題引起了大量專家學(xué)者的注意，很多實(shí)用有趣的成果見諸報(bào)道。例如通過多自主無人車輛的智能感知與協(xié)同控制，可以實(shí)現(xiàn)無人車之間的間距控制，達(dá)到減少交通擁堵、降低尾氣排放和保護(hù)環(huán)境等目標(biāo)[1-2]。通過多無人機(jī)編隊(duì)控制[3]、多移動(dòng)舞臺(tái)機(jī)器人協(xié)同控制[4]等可以變換出許多有意義的圖案或者保持某種隊(duì)形運(yùn)動(dòng)，給觀眾帶來無與倫比的視覺體驗(yàn)。另外，在無線傳感網(wǎng)絡(luò)中通過多智能體系統(tǒng)協(xié)同控制理論和方法可以對(duì)目標(biāo)的狀態(tài)進(jìn)行更好的探測(cè)、定位和預(yù)測(cè)[5]。

通常多智能體系統(tǒng)中各個(gè)智能體之間都是基于網(wǎng)絡(luò)傳輸，因此可能會(huì)存在復(fù)雜的網(wǎng)絡(luò)攻擊和不確定環(huán)境干擾等問題[6-7]。例如，F(xiàn)eng等[8]研究了基于事件觸發(fā)安全協(xié)同控制策略下遭受DoS攻擊的線性多智能體系統(tǒng)，并分析了安全平均一致問題下DoS攻擊的頻率和持續(xù)時(shí)間。Ni等[9]提出了針對(duì)存在DoS攻擊下連續(xù)時(shí)間異構(gòu)線性多智能體網(wǎng)絡(luò)基于魯棒隨機(jī)采樣數(shù)據(jù)的輸出反饋一致控制器設(shè)計(jì)方法。然而以上研究中攻擊行為的統(tǒng)計(jì)概率信息都是確定已知的，但在實(shí)際情況下往往很難精確地獲取相關(guān)攻擊信息，因此研究不確定的DoS攻擊下系統(tǒng)協(xié)同控制問題將更具現(xiàn)實(shí)意義。另外，當(dāng)攻擊發(fā)生時(shí)，多智能體之間的通信將被阻塞甚至完全打斷，各個(gè)智能體之間的通信連接情況不再是某一單一的狀態(tài)，而是在不斷發(fā)生變化。馬爾可夫切換系統(tǒng)方法通常被用來描述此類參數(shù)突變的實(shí)際系統(tǒng)，關(guān)于馬爾可夫切換系統(tǒng)的研究已經(jīng)有了很多重要的結(jié)果，其涵蓋的領(lǐng)域有系統(tǒng)穩(wěn)定性分析、濾波器設(shè)計(jì)和控制器合成等[10-12]。例如，Lam等[13]和Wu等[14]分別研究了基于馬爾可夫切換系統(tǒng)方法的H∞魯棒控制和滑模控制問題，Zhang等[15]針對(duì)DoS攻擊下的異構(gòu)線性多智能體系統(tǒng)提出了一種新的切換系統(tǒng)方法并給出了攻擊強(qiáng)度和一致性能之間的數(shù)量關(guān)系。然而，大部分已知的關(guān)于馬爾可夫切換系統(tǒng)工作無論是應(yīng)用于控制還是濾波都基于一個(gè)重要的假設(shè)，那就是控制器/濾波器始終可以完全獲取設(shè)備的狀態(tài)信息以確保控制器/濾波器模式始終與系統(tǒng)模式同步運(yùn)行。因此，所設(shè)計(jì)的控制器被稱為模式相關(guān)控制器或同步控制器，然而在實(shí)際應(yīng)用中，這種理想的假設(shè)是很難成立的。

基于對(duì)上述問題的觀察和分析，針對(duì)在復(fù)雜網(wǎng)絡(luò)攻擊下的基于有向通信傳輸?shù)漠悩?gòu)線性多智能體系統(tǒng),設(shè)計(jì)了一個(gè)異步輸出反饋控制器來解決：1)不確定發(fā)生的DoS攻擊導(dǎo)致基于固定數(shù)據(jù)采樣周期通信的系統(tǒng)模型發(fā)生不確定的變化從而造成系統(tǒng)失控和2)由于攻擊行為的復(fù)雜以及網(wǎng)絡(luò)誘導(dǎo)時(shí)延、丟包等產(chǎn)生的系統(tǒng)模型-控制器異步現(xiàn)象。首先通過使用馬爾可夫切換系統(tǒng)方法來構(gòu)建系統(tǒng)模型，并將攻擊發(fā)生的不確定性描述為在一個(gè)凸包面上分布的狀態(tài)轉(zhuǎn)移概率矩陣，然后設(shè)計(jì)一個(gè)靜態(tài)輸出反饋控制器并引入馬爾可夫鏈來描述系統(tǒng)和控制器之間的異步現(xiàn)象。本文所提出方法主要有兩個(gè)益處：1)所遭受的攻擊信息可以是確定、不確定甚至是完全未知的，因此在實(shí)際應(yīng)用中能夠取得更好的效果；2)所設(shè)計(jì)的異步控制器包含了常見的模型獨(dú)立控制器(M={1})和同步控制器(M=N且μsφ=1)，具有更為廣泛的通用性，實(shí)際應(yīng)用中限制更小。

1 預(yù)備知識(shí)和問題引入

1.1 圖論基礎(chǔ)

首先介紹一些圖論中的基本概念。由集合(v，ε)構(gòu)成一個(gè)有向圖G，其中V={v1,v2,…,vn}表示具有n個(gè)節(jié)點(diǎn)的集合，ε?V×V是有序節(jié)點(diǎn)對(duì)構(gòu)成的邊集合。如果在圖G中的任意兩個(gè)節(jié)點(diǎn)都是連通的，則可以稱此有向圖G是連通圖。鄰接矩陣定義為A=[aij]，當(dāng)(νi,νj)∈ε時(shí)aij>0，表示節(jié)點(diǎn)i可以從節(jié)點(diǎn)j獲得信息，否則aij=0。節(jié)點(diǎn)i的鄰居集合被定義為Ni={j∶aij>0}。矩陣D=diag{di}稱為入度矩陣，其中di=∑j∈Niaij是節(jié)點(diǎn)i的入度權(quán)重，拉普拉斯矩陣定義為L=D-A。牽引矩陣G=diag{g1,g2,…,gn}表示領(lǐng)導(dǎo)者和跟隨者之間的交互關(guān)系，如果第i個(gè)跟隨者能夠獲得領(lǐng)導(dǎo)者信息，則有g(shù)i>0，否則gi=0。更多圖論的詳細(xì)介紹可以參考文獻(xiàn)[16]。

假設(shè)1有向圖G是連通圖并且其中沒有孤立的點(diǎn)。

假設(shè)2[17]DoS攻擊持續(xù)的時(shí)間是有界的并且攻擊行為的變化滿足馬爾可夫過程。

1.2 攻擊描述和系統(tǒng)建模

在本文中，假定有一個(gè)領(lǐng)導(dǎo)者和n個(gè)跟隨者，領(lǐng)導(dǎo)者模型為:

(1)

式中：x0(t)∈m，y0(t)∈q分別是領(lǐng)導(dǎo)者的狀態(tài)變量和測(cè)量輸出，m×m和q×m是兩個(gè)常數(shù)矩陣。

跟隨者的模型描述為:

(2)

式中：xi(t)∈ni、ui(t)∈pi、ωi(t)∈mi和yi(t)∈q分別是第i個(gè)智能體的狀態(tài)、輸入、擾動(dòng)和輸出，在異構(gòu)多智能體系統(tǒng)中，常數(shù)矩陣Ai，Bi，Ci，Di一般各不相同。

由于所設(shè)計(jì)的控制系統(tǒng)通常都是采用數(shù)字方式，因此本文假定每一個(gè)智能體都能夠周期地觸發(fā)采樣過程，類似基于數(shù)據(jù)采樣通信過程可參考文獻(xiàn)[18]。正常情況下系統(tǒng)以T0為固定采樣周期進(jìn)行采樣，然而由于DoS攻擊的存在導(dǎo)致通信連接被破壞，由于每一個(gè)智能體采用保持輸入機(jī)制來更新狀態(tài)，因此隨著攻擊持續(xù)的時(shí)間不同，采樣周期hk=tk+1-tk將會(huì)變?yōu)?T0，3T0，4T0,…，假設(shè)hk取值于一個(gè)有限集合R，即hk∈R={δ1T0,δ2T0,…,δNT0}，其中δj,j=1,2,…,N是正整數(shù)。將采樣時(shí)刻tk簡記為k，定義馬爾可夫鏈{ρ(k),k∈+}用來描述DoS攻擊過程，ρ(k)∈N?{1,2,…,N}，概率轉(zhuǎn)移矩陣Λ={πst}，轉(zhuǎn)移概率定義為Pr(ρ(k+1)=t|ρ(k)=s)=πst且有對(duì)于任意的s,t∈N有πst>0和則多智能體系統(tǒng)的模型可以分別描述如下:

領(lǐng)導(dǎo)者為

(3)

跟隨者為

(4)

上述式中有：

(5)

(6)

但是在實(shí)際中由于攻擊者會(huì)刻意隱藏其攻擊行為導(dǎo)致很難精確獲取相關(guān)攻擊信息，因此轉(zhuǎn)移概率矩陣Λ={πst}中的某些元素可能是不確定甚至完全未知的，為此本文將用一個(gè)凸多面體來描述概率轉(zhuǎn)移矩陣中有界但不確定的元素，具體形式為

(7)

其中Λr=[πst],s,t∈N,r=1,…,是包含不確定元素的狀態(tài)轉(zhuǎn)移概率矩陣，αr∈[0,1]，是凸多面體中面的個(gè)數(shù)。為便于分析，定義N=N其中：

(8)

不確定和未知的元素分別用上標(biāo)“～”和“^”表示。

此外，由于攻擊行為過于復(fù)雜以及各種網(wǎng)絡(luò)傳輸問題，控制器所獲取的模型信息往往是不準(zhǔn)確的，因此控制器模態(tài)可以視為是系統(tǒng)模態(tài)的觀測(cè)值，兩者之間存在異步現(xiàn)象。本文設(shè)計(jì)的控制器為

(9)

(10)

定義下列誤差信號(hào):

(11)

和下列符號(hào):

(12)

于是可以得到閉環(huán)系統(tǒng)

(13)

其中：

(14)

1.3 多智能體系統(tǒng)一致性問題

輸出一致性問題描述如下：

問題1[21]設(shè)計(jì)控制器(9)使得：

1)當(dāng)ωi(k)=0且在非零初始條件下有

(15)

成立，其中χ(0)={ηi(0),εi(0),ρ(0),σ(0)}表示初始條件。

2)當(dāng)ωi(k)∈l[0,∞)且在零初始條件下有

(16)

成立，其中γ是一個(gè)正數(shù)(魯棒增益)。

為了解決問題1，本文需要一個(gè)合適的引理來處理有向圖，根據(jù)假設(shè)1可知L+G為正定矩陣[22]，首先引入一個(gè)非奇異矩陣U∈n×n使得

U-1(L+G)U=J

(17)

其中J是L+G的約旦標(biāo)準(zhǔn)型，λi是它的對(duì)角元素且有Re(λ1)≤Re(λ2)≤…Re(λn)。對(duì)于任意復(fù)數(shù)特征值λ，定義分解形式為

(18)

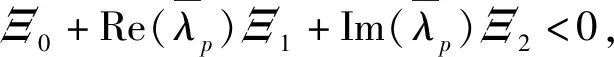
Ξ0+Re(λp)Ξ1+Im(λp)Ξ2<0

(19)

成立，其中Ξ0，Ξ1和Ξ2是與特征值無關(guān)的實(shí)對(duì)稱矩陣。

在得出主要結(jié)論之前，還需要引入以下幾個(gè)引理：

引理2對(duì)于具有適當(dāng)維度的矩陣T，M，U和W，T+(MW)y<0成立充分條件為

(20)

引理3存在正定矩陣Q使得不等式-QTⅡ-1Q≤-Q-QT+Ⅱ?qū)τ谌我鈱?shí)矩陣Ⅱ≥0都成立。

(21)

2 問題分析與主要結(jié)果

2.1 一致性問題轉(zhuǎn)化和系統(tǒng)降維

定理1問題1可解，即異構(gòu)多智能體系統(tǒng)一致性得到保證等價(jià)于低階閉環(huán)系統(tǒng)

(22)

均方漸近穩(wěn)定和低階閉環(huán)系統(tǒng)

(23)

均方漸近穩(wěn)定且具有魯棒增益γ≥0，其中λi是拓?fù)渚仃嘗+G的非零特征值。

證明可以找到一個(gè)非奇異矩陣U∈n×n使得

(24)

其中：

易知，上式等價(jià)于如下的n個(gè)低階系統(tǒng)

(26)

同步漸近穩(wěn)定，其中：

(27)

2.2 基于Lyapunov理論分析系統(tǒng)穩(wěn)定性

定理2如果對(duì)于任意的s∈N和φ∈M存在魯棒系數(shù)γ≥0，一系列正定對(duì)稱矩陣Pρ(k)以及控制器增益Fσ(k)和Kiσ(k)使得下列不等式

(28)

(29)

成立，那么問題1可解，其中：

(30)

(31)

(32)

(33)

定義：

(34)

那么可得

(35)

其中有：

(36)

(37)

其中有

(38)

(39)

(40)

于是可得

E{ΔV(zi(k),k)}=

(41)

根據(jù)式(28)可知E{ΔV(zi(k),k)}≤0。

(42)

將不等式兩邊從0累加到∞有

(43)

2)對(duì)于隨機(jī)系統(tǒng)(23)，分別考慮ωi(k)=0和ωi(k)≠0兩種情況。

(44)

(45)

b)當(dāng)ωi(k)≠0時(shí)，有

(46)

(47)

于是可以得到

(48)

根據(jù)式(29)并使用引理4可知H≤0，對(duì)Hamiltonian函數(shù)兩邊從k=0累加到∞有

E{V(∞)-V(0)}+

(49)

由于零初始條件V(0)=0和V(∞)>0可以得

(50)

也就是

(51)

定理2雖然給出了解決問題1的充分條件，然而并不能直接方便的用來求解控制器(9)，為了克服這個(gè)困難，本文通過運(yùn)用一系列矩陣變換方法得出定理3。

2.3 基于LMI求解控制器增益

(52)

(53)

其中Ξiφ、Υ為自行設(shè)定的參數(shù)矩陣，且有：

(54)

(55)

(56)

(57)

(58)

(59)

(60)

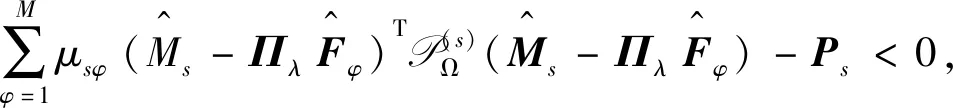
(61)

(62)

應(yīng)用引理4有

(63)

上、下矩陣不等式分別左、右乘以對(duì)角矩陣diag{I,G,…,G}T，diag{I,H}T和它們的轉(zhuǎn)置后，應(yīng)用引理3可得

(64)

(65)

2)同理存在ε>0使得

(66)

(67)

應(yīng)用引理4可得

(68)

再一次應(yīng)用引理4有

(69)

(70)

由于ψisφ=Ais+BisKiφCi，那么

(71)

可以寫成

(72)

(73)

定義：

(74)

通過使用引理2可知(53)成立。

為了便于更清晰地理解本文算法整體思想，見表1，給出了異步控制器具體設(shè)計(jì)求解的步驟。

表1 異步控制器求解過程Tab.1 Solving process of asynchronous controller

3 仿真驗(yàn)證

本章基于移動(dòng)舞臺(tái)機(jī)器人系統(tǒng)進(jìn)行了仿真研究，證明所提出方法的有效性。現(xiàn)在常用的移動(dòng)舞臺(tái)機(jī)器人系統(tǒng)一般采用輪式結(jié)構(gòu)，可以很方便的建立數(shù)學(xué)模型用來研究協(xié)同控制問題。

圖1 舞臺(tái)機(jī)器人系統(tǒng)結(jié)構(gòu)Fig.1 Structure of stage robot system

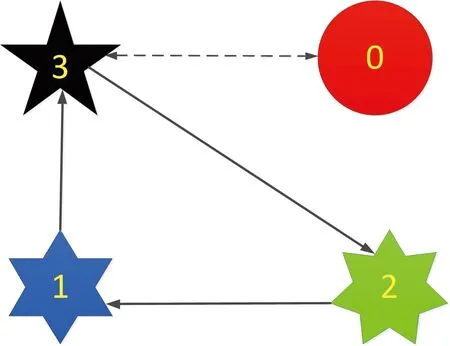
圖2 通信連接拓?fù)銯ig.2 Communication connection topology

(75)

其中{ai,bi,ci,di,ei}分別取值為{2,1,1,10,1}，{2,1,1,3,1}，{2,2,1,10,1}。領(lǐng)導(dǎo)機(jī)器人模型見式(76)。

(76)

假設(shè)3個(gè)跟隨機(jī)器人受到的干擾信號(hào)分別為0.5sin(k)，sin(k)，-sin(k)。根據(jù)式(10)可以計(jì)算得到：

(77)

正常情況下系統(tǒng)的采樣周期設(shè)定為T0=0.01，設(shè)定最大攻擊持續(xù)時(shí)間為2T0，DoS攻擊持續(xù)時(shí)長的概率轉(zhuǎn)移矩陣為

(78)

控制器和系統(tǒng)模態(tài)異步的概率轉(zhuǎn)移矩陣為

(79)

(80)

(81)

在仿真中，選擇初始條件為

(82)

DoS攻擊的觸發(fā)和控制器異步狀態(tài)分別見圖3、4，從圖5(位置跟蹤)和圖6(跟蹤誤差)可以看出異構(gòu)移動(dòng)舞臺(tái)機(jī)器人系統(tǒng)的一致性基本能夠被滿足。

圖3 系統(tǒng)狀態(tài)Fig.3 System state

圖4 控制器狀態(tài)Fig.4 Controller state

圖5 實(shí)時(shí)位置跟蹤Fig.5 Real-time location tracking

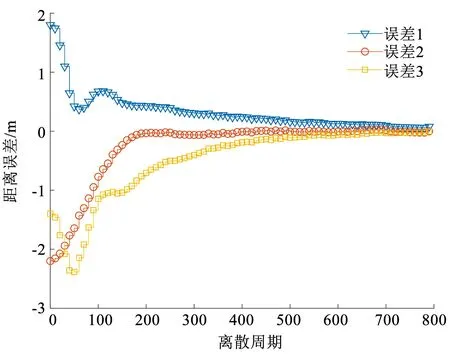
圖6 跟蹤距離誤差Fig.6 Tracking distance error

魯棒性是衡量系統(tǒng)性能的一個(gè)重要指標(biāo)，其體現(xiàn)了系統(tǒng)對(duì)抗外界干擾的能力，本文所設(shè)計(jì)的異步控制器具有較好的兼容性，包含了普通的模式獨(dú)立控制器和同步控制器。在完全相同的系統(tǒng)模型和初始條件下，分別采用普通的模式獨(dú)立控制器和同步控制器以及本文所設(shè)計(jì)的異步控制器，仿真計(jì)算得出其系統(tǒng)魯棒性系數(shù)γ分別為1.293 1、1.106 8和0.915 5。可以驗(yàn)證使用本文所設(shè)計(jì)的異步控制器時(shí)系統(tǒng)具有更好(小)的魯棒性能，表現(xiàn)為抗干擾能力更強(qiáng)，即系統(tǒng)魯棒性能更優(yōu)。

4 結(jié) 論

本文考慮了不確定DoS攻擊下由于系統(tǒng)模態(tài)獲取困難引起的控制器-系統(tǒng)模型異步問題。引入馬爾可夫過程來描述系統(tǒng)所遭受的攻擊以及與控制器之間的異步現(xiàn)象，給出了更為全面的系統(tǒng)建模方法，然后結(jié)合所設(shè)計(jì)的輸出反饋控制器通過解耦技術(shù)將原高維系統(tǒng)轉(zhuǎn)換為兩個(gè)低維的閉環(huán)誤差系統(tǒng)，并且通過應(yīng)用Lyapunov穩(wěn)定性理論得到了保證異構(gòu)多智能體系統(tǒng)輸出一致性的充分條件。進(jìn)一步，結(jié)合相關(guān)矩陣變換方法給出了通過求解一系列矩陣不等式來獲得控制器增益的方法。最后，通過基于移動(dòng)舞臺(tái)機(jī)器人系統(tǒng)的仿真研究驗(yàn)證了本文所提出方法的有效性。