基于壓力拱理論的雙洞隧道最小凈距彈塑性分析
宋 蕾 付晨濤
(1.西安科技大學高新學院城市建設學院,陜西 西安 710054;2.啟迪設計集團股份有限公司,陜西 西安 710054)
隨著我國隧道建設的飛速發展,單洞隧道已難滿足運輸需求,隧道由最初的小直徑單洞隧道發展至現在的超大直徑雙洞隧道,雙洞隧道之間的間距取值規范雖有明確,但是實踐表明,在目前某些特定的工況下規范的間距取值依舊過于保守,因此,選取雙洞隧道間的最優凈距是目前迫切需要研究的問題。
當前的研究中,凈距的取值多集中在利用數值模擬、現場實際量測和模型模擬方法。而在理論分析方面主要是運用復變函數Schwarz轉換的相關數學知識,推導出應力場,從而確定合理凈距。
本文以彈塑性理論為基礎進行分析,將雙洞隧道中間巖柱劃分成塑性區和中間核區,利用普氏壓力拱理論的相關原理,對雙洞隧道中間巖柱體應力分布進行合理化簡,從而確定出雙洞隧道最小凈距的計算公式。
1 雙洞隧道壓力拱理論
1.1 雙洞隧道壓力拱的形式
壓力拱的形成分以下兩種極限狀況[1]。
隧道開挖方式,中間巖柱體加固措施合理的情況下,會提高加固后的中間巖柱體承載能力,有效防止巖柱體上方土體的下沉,縮小了壓力拱的影響范圍,在該狀態下,雙洞隧道只能出現單側洞壓力拱,且左右隧道的壓力拱影響范圍互不干擾。
隧道開挖方式,中間巖柱體加固措施不妥的情況下,會導致中間巖柱體承載能力降低,隨著巖體上方土體的逐步下沉,這導致了左右洞室的壓力拱影響范圍逐漸擴大,直至最后在洞室上空兩個壓力拱相互重合,這就是極限壓力拱的形成。
本文采用第二種極限工況下的雙洞隧道受力形式,來分析探討雙洞隧道的重力荷載分布情況。
1.2 壓力拱高度的取值
普氏理論認為,在松散巖體中進行隧道開挖,隧道上方會形成一個拋物線壓力拱用于承受上部巖體的重力荷載,而作用在隧道支護結構上的圍巖壓力僅為壓力拱內巖體的自重。
2 雙洞隧道物理模型的建立
此處考慮側壓力系數為1的情況,由卡斯特納公式[2]可知,單洞隧道塑性區半徑如下:
式1
則單洞隧道塑性區范圍為:
式2
將雙洞隧道中間巖柱劃分成塑性區和中間核區,這里選取中間巖柱寬為s,高L=2ra為研究對象,如圖1所示。
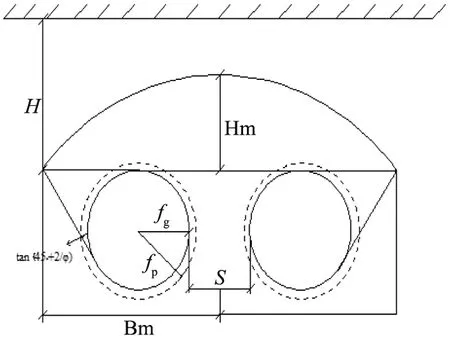
圖1 雙洞隧道物理模型
3 建立中間巖柱的力學模型
根據摩爾庫倫準則和靜力平衡方程得到無支護圓形洞室塑性區應力計算表達式[2]。
式3
根據式3中環向應力公式得在塑性區與中間核區的交界處的環向應力等于當r=rp時的環向應力值,中間巖柱核區邊界處所受豎向應力為。
式4
兩側隧道會對中間巖柱的應力大小產生影響,設中間巖柱塑性區的應力大小是從0線性增長到核心區巖柱所能承受的最大應力,且核心區應力大小保持不變。該應力分布如圖2所示。
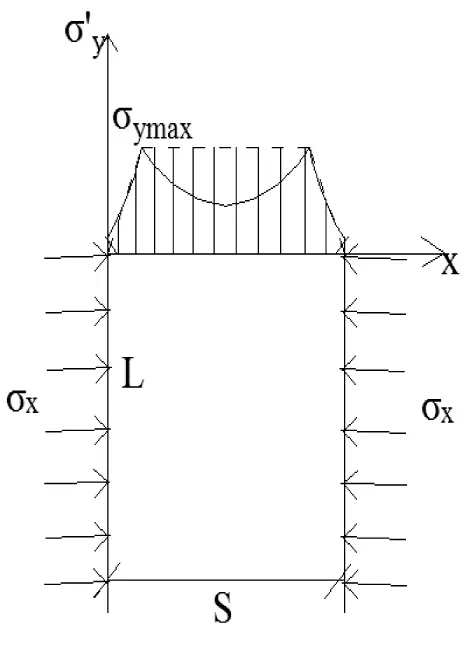
圖2 中間巖柱的應力分布圖
這里將圍巖壓力拱內的重力荷載分布簡化為矩形分布,當隧道開始開挖后,認為兩側隧道(各一半)的重力荷載將分配到中間巖柱上[3]。
4 雙洞隧道最小凈距公式的推導
由圖2中應力分布曲線可知,中間巖柱受力為:
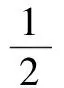
式5
利用普氏理論求得極限壓力拱高度為:
式6
通過荷載簡化,假定荷載在隧道拱頂呈矩形分布,中間巖柱所受的荷載高度為Hm,推導出中間巖柱所受重力荷載為:
式7
由式5和式7相等,賦值分析得雙洞隧道最小凈距為
式8

5 參數分析
本文以Ⅲ級圍巖常見的物理力學參數為例,分析式8中各個物理量對雙洞隧道最小凈距的影響關系,得到以下結論。
最小凈距隨重度的增大而非線性增大,但在Ⅲ級圍巖條件下基本呈線性關系且重度對最小凈距取值影響不大。
最小凈距隨粘聚力及內摩擦角的增大而呈非線性減小的趨勢,且該參數對隧道凈距的取值影響較大。
當計算內摩擦角逐漸增大時,最小凈距的變化呈非線性減小,且非線性變化并不明顯,所以該參數對雙洞隧道最小凈距影響較小。
隨著隧道埋深逐漸變大,最小凈距的變化成非線性增大,在Ⅲ級圍巖條件下非線性趨勢明顯。根據實際情況,在Ⅲ級圍巖條件下開挖雙洞隧道時,隧道凈距應取0.5D較為合理。
6 小 結
將中間巖柱分為塑性區和中間核區,基于壓力拱理論與彈塑性理論相結合,得到了雙洞隧道最小凈距確定公式8。
對式8中所涉及到的物理力學參數進行分析,分別得到最小凈距與各參數之間的關系;本文給出的推導利用了壓力拱理論,且考慮了埋深對凈距的影響使中間巖柱的尺寸更加優化,對提高經濟效益和隧道施工安全有著重要意義。

