大跨度人行橋舒適性分析和TMD減振設計

宋 ?

[上海市政工程設計研究總院（集團）有限公司，上海市 200092]

0 引言

隨著城市人行橋對景觀要求的提高，人行橋越來越多地向著輕柔和大跨度方向發展。為了避免共振，減少行人不安全感，我國《城市人行天橋與人行地道技術規范》中規定，人行橋結構豎向自振頻率不應小于3 Hz。而對于大跨度人行橋而言，自振頻率很難達到3 Hz 以上。若要滿足規范要求，就會造成材料的浪費,而且效果有限。另外，對于大跨度柔性結構的人行橋來講，橫向振動的問題也同樣突出，但是我國規范中也并未涉及。本文比較了各國人行橋舒適性評價標準和常用的減震措施，以一座百米級人行橋為例，按照《德國人行橋設計指南EN03》對橋梁進行舒適性分析并采用調諧質量阻尼器（TMD）進行減振。結果表明，有效提高了橋梁的舒適性。

1 國內外規范人行橋舒適性評價指標

我國《城市人行天橋與人行地道技術規范》中規定，人行橋結構豎向自振頻率不應小于3 Hz，使之避開人橋共振的敏感頻率范圍。研究表明，振動的位移、速度和加速度3 個要素中，影響人的生理和心理感受的最主要因素是加速度[1]。因此，國外規范在頻率難以滿足的情況下，增加了關于加速度的評價指標（見表1）。

表1 國外規范人行橋舒適性評價標準

上述國外規范基本采用了橋梁自振頻率限制與加速度限制相結合的方法。首先采用橋梁自振頻率進行評價，當不滿足頻率要求時，采用加速度指標進行評價。對比上述各規范可知，《德國人行橋設計指南EN03》最完善，不僅規定了豎向與橫向的加速度限制，還進一步劃分了從舒適到不可忍受4 個等級。因此，本文推薦采用《德國人行橋設計指南EN03》指標評價人行橋的舒適性。

2 TMD 減振設計

對于無法滿足舒適性要求的人行橋需要采用一定措施進行減振，TMD 具有簡單、有效、易更換等優點，因此被廣泛用于人行橋的減振控制。

2.1 TMD 減震原理

TMD 由固體質量、彈簧和阻尼器組成。TMD 系統為被動受力模式，當主結構振動時，子結構產生一個與振動方向相反的慣性力作用在主結構上，從而使主結構的振動減小。

2.2 TMD 參數設計

TMD 需要設計的參數主要包括質量比、頻率比和阻尼比。一般情況下，質量越大，減振效果越好，但是過大的質量會增加TMD 的施工難度，也會增加橋梁的恒載。因此，通常情況下，質量與控制模態的廣義質量比值取1%～5%[1]。最優頻率比和阻尼比的取值需要根據位移、加速度等不同的優化目標來選取不同的計算式。人行橋一般情況下的減振優化目標為加速度，此時最優頻率αopt比和最優阻尼比ξopt按式（1）、式（2）確定：

當確定了質量比、頻率比和阻尼比之后，便可按式（3）～ 式（6）計算TMD 的頻率fd、質量md、彈簧剛度kd、阻尼系數cd等參數。

式中：Mj為控制模態的廣義質量。

在實際設計當中，一般先通過上式計算得到合理的質量范圍，再選用常規的TMD 質量規格，反算得到廣義質量比μ，然后計算得到其他的設計參數。

3 實橋應用

3.1 項目概況

主橋上部結構為拱形鋼桁架，板桁結合體系。橋梁跨徑布置為2+100+2=104 m，橋寬11m，跨中桁高7.2 m。橋梁雙層設置，上層設置3 m 寬景觀步道，下層兩側各挑出4 m 寬人非道。橋梁總體布置和跨中斷面如圖1、圖2 所示。

圖1 橋梁總體立面圖（單位：m）

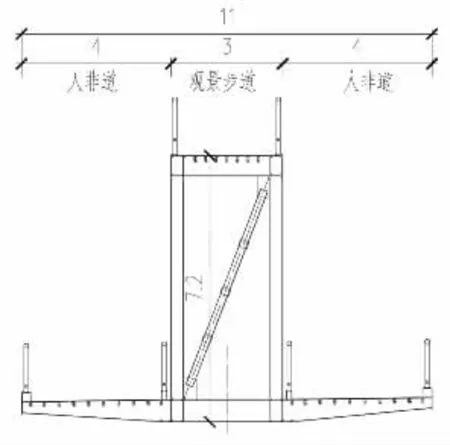
圖2 橋梁跨中斷面圖（單位：m）

3.2 橋梁動力特性

評價人行橋舒適性，首先需要計算橋梁動力特性，校核各模態頻率是否處于臨界范圍之內。若高于臨界頻率，則無須進一步計算，即可認為舒適性滿足要求；否則需要通過加速度來判斷橋梁的舒適度。本橋空間有限元模型采用了板殼單元和梁單元。其中，橋面板采用板單元，主桁桿件及橋墩、承臺采用梁單元，模型示意圖如圖3 所示。計算得到前10 階振型見表2。

圖3 空間有限元模型示意圖

表2 人行橋前10 階振動模態

根據《德國人行橋設計指南EN03》，人行橋頻率fi的臨界范圍是：一階豎向和縱向振動1.25 Hz≤fi≤2.3 Hz，二階豎向和縱向振動2.5 Hz≤fi≤4.6 Hz；水平振動0.5 Hz≤fi≤1.2 Hz，水平振動不受二階簡諧行人荷載影響。

由表2 可知：模態1 為頻率處于水平振動臨界范圍內，模態2、3、4 處于一階豎向和縱向振動臨界范圍之內或附近，模態5、7 振動處于二階豎向和縱向振動臨界范圍內。因此，模態2、3、5、7 需要考慮人行橋的豎向舒適度問題，模態1 需要考慮人行橋的水平舒適度問題。

3.3 荷載工況

因為本橋為空間桁架結構，雙層人行橋，大部分振型是多方向耦合，無法采用逐個模態驗算的方式，故采用時程法計算最大加速度響應。人行激勵荷載的作用方向根據所計算的振型形狀加載，如圖4 所示。

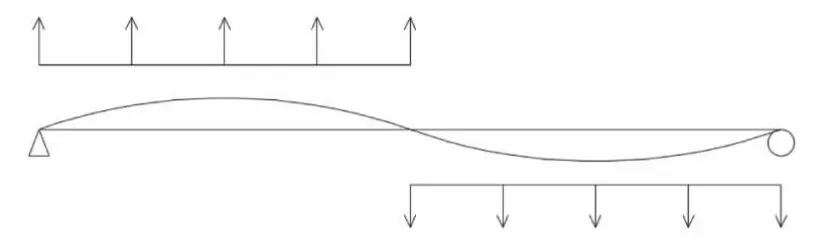
圖4 人行激勵荷載加載形式示意圖

人行激勵荷載模型取《德國人行橋設計指南EN03》提供的連續步行荷載（N/m2），如式（7）所示:

式中：P 為步行頻率為fs時，單個行人產生的荷載幅值，對側向激勵取35 N，對豎向激勵取280 N；fs按驗算工況所取模態的頻率取值；t 為時間；ψ 為考慮步頻接近基頻變化范圍臨界值的概率而引入的折減系數，本工程偏于安全的對一階人行荷載取1.0，對二階人行荷載取0.25；N＇為等效行人數，當人行密度小于1.0 P/m2時，

式中：ξ 為振型阻尼比，n 為總人數。

人行密度大于1.0 P/m2時，取

根據上文分析，共有5 個振型模態需要考慮舒適性問題，因此共建立5 個荷載工況進行計算分析，荷載參數取值見表3。

表3 荷載參數

3.4 舒適性評價

選取各工況對應振型位移最大點作為加速度觀測點，各工況觀測點位置及其加速度最大值見表4。

由表4 可知，本橋在工況4、工況5 下豎向加速度小于0.5 Hz，達到最佳舒適度標準；工況2 和工況3 下，豎向振動未達到最佳舒適度標準，需要采取措施進行振動控制；工況1 下，水平振動未能達到最佳舒適度標準，需要采取措施進行振動控制。

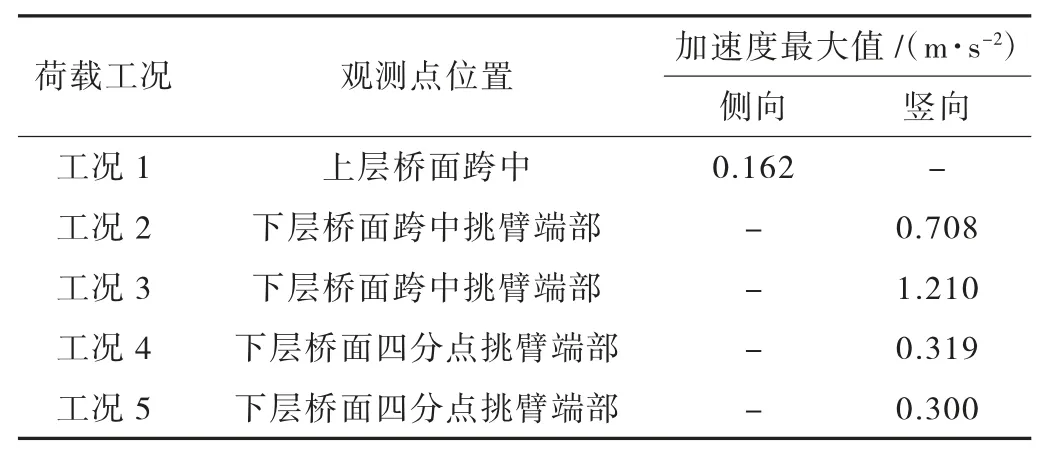
表4 各個工況下觀察點的加速度值

3.5 TMD 減振設計及效果

本橋采用TMD 進行減振設計。研究表明，TMD放置于位移最大處效果最明顯。根據振型1，放置1個TMD 于上層橋面跨中處，控制水平方向；根據振型2，放置2 個TMD 于跨中處兩側挑臂端部，控制豎向振動；根據振型3，放置2 個TMD 于跨中處桁架下弦桿處，控制豎向振動，共5 個TMD。其參數見表5，其布置圖如圖5 所示。

表5 TMD 參數

圖5 TMD 設置位置示意圖

布置TMD 后，重新對工況1、2、3 進行計算，測點在各個工況下的最大加速度值見表6。

表6 各個工況下觀測點的加速度值

TMD 減振效果采用減振率表示，其計算公式為：

各工況下觀測點的減振率見表7。

表7 各個工況下觀測點的減振率

采用TMD 減振措施后，橋梁豎向最大加速度為0.081 m/s2,小于0.5 m/s2，滿足豎向振動舒適性要求；橫向最大加速度為0.017 m/s2，滿足橫向舒適性要求，縱、橫向減振效率均達到了90%左右，效果顯著。

4 結語

（1）由于我國人行橋規范舒適性評價并不適用于大跨度橋梁，比較國內外各規范后，推薦采用《德國人行橋設計指南EN03》的指標來進行人行橋的舒適度分析。

（2）以一座百米級空間桁架人行橋為列，進行了舒適度分析，并結合橋梁的實際情況設計了TMD 的減振措施。分析結果表明，其減振效果顯著。