電力系統潮流計算的計算機程序設計
宋天祥
(重慶湘渝鹽化股份有限公司,重慶 萬州 404000)
電能在現代社會發展中發揮著越來越重要的作用,穩定可靠的電能供應是當代社會和生活中必不可少的因素。電力系統潮流計算是分析電力系統運行方式的三大基本計算之一,也是短路和穩定計算的基礎,是研究電網規劃和運行的基本工具。但是電力潮流計算過程十分繁瑣,在當前計算機技術發展的背景下,如何利用計算機輔助計算復雜電力系統潮流問題成為當前學術界關注的熱點問題。因此,在研究工作中進行潮流計算和相關運算分析,具有一定的迫切性。基于此,本文在MATLAB技術支持下對電力系統潮流計算的相關程序進行設計研究,以期能夠為電力系統的運行提供支持。
1 電力系統潮流計算基本概念
隨著社會的發展,能源成為當前社會進步和技術應用的關鍵,電能作為一種潔凈能源,能夠通過多種綠色方式產生,比如風能發電、水能發電等技術。這些資源的運用具有一定的地域性,如何將電能傳輸至用電區是解決電力分配的重要工作。電能的傳輸一直都是電力事業發展的重要領域,提高發電和輸電的效率是必要的,特別是在輸電過程中損耗較大,使得大量的資源和能源被無情地消耗掉。對電力系統中用電效率的提升,成為了當今科學家們所要研究的最為急切的問題。在電力系統正常運行過程中,系統中從電源到負荷各節點的電壓、電流的大小和方向以及功率的穩態分布,這個過程稱為電力系統的潮流分布,電力系統的潮流分配過程中,每一條線路、每一條母線所分得的功率是多少,這個過程叫做潮流計算過程。因此本文的研究對于電力系統的安全運營與維護具有重要參考意義。
2 潮流計算的基本方法
潮流計算的計算方法有很多,現階段比較成熟的方法是牛頓拉夫遜法、前推回代法和最小功率法等,在牛頓拉夫遜法的基礎上,通過簡化有功功率和頻率,無功功率和電壓的對應關系提出了PQ分解法等。在人工智能算法逐漸發展的今天,也有很多人工智能的黑箱方法用來潮流計算,但人工智能方法進行潮流計算準確度不高,在實際運行中,需要準確度較高的潮流計算方法。
2.1 高斯-塞德爾原理
在潮流研究中,首先必須解出非線性方程,對于每個節點有兩個未知變量。用高斯-賽德爾法(Gauss-Seidel Power Flow Solution)求解Vi,改寫為式(1-1)
(1-1)
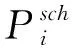
(1-2)
上述的公式包括輸電線路和接地之間產生的電導和電納。因為平衡節點在實際運行過程中和潮流計算過程中是給定電壓幅值和電壓相角參數的,因此,平衡節點規定的標幺值幅值為1,相角為0,他是屬于在潮流計算中的參考節點。在潮流計算實際運行的過程中,各個功率節點的實際功率大小要高于參考值,它們的相位要滯后于參考值功率節點電壓和相角的具體大小,取決于負荷的功率需求。并且與實際的運行狀態相關。
2.2 PQ分解法基本原理
計算潮流的PQ分解法。根據牛頓法對潮流程序進行改進和簡化的基礎上,提出了PQ分解法(又稱改進牛頓法)。它的主要思想是節點功率表示為一個方程在極坐標下的電壓矢量,理解基本矛盾,有功功率誤差作為電壓矢量角校正的基礎,和無功功率誤差作為電壓振幅校正的基礎。有功功率和無功功率是分離迭代。對于PQ解法下的方程式如下式:
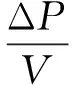
(1-3)
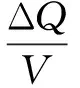
(1-4)
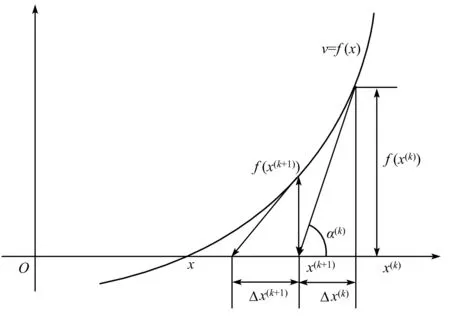
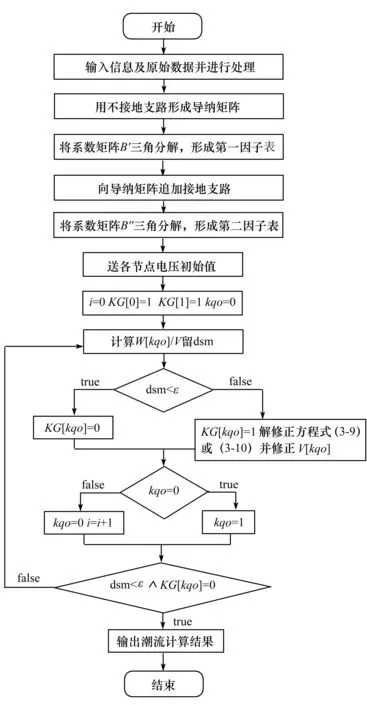
上述方程式是PQ解法的簡化形式,式中的V是電力系統中的節點電壓幅值,表示為一種對角矩陣形式。B′與B″之間有著階數的差異性,具體表現為B′為n-1階,則B″為 為了保持該方程式的收斂性,一般情況下將電力系統的導納矩陣為虛部,對此,在進行計算過程中一般采用以下形式進行: 忽略輸電線路充電容量以及充電電容對輸電線路整體參數的影響。公式進行相應的變換如下所示: (1-5) 式中V0為系統平均電壓。此外在程序中可以用導納矩陣中元素的虛部作為B′。快速分解法所建立的前提,是對原有的電力系統模型進行極限簡化和理想狀態簡化的方法基礎上進行的,實際的元件中電阻和電抗的大小,沒有辦法達到原來的假定情況,因此會造成系統在運算過程中迭代出現問題。 牛頓迭代法是取x0,在此基礎上,求出比x0更接近的方程的解,通常情況下,負載功率應用于每個總線是已知的,但每個節點的電壓是未知的(平衡節點除外)。根據網絡結構可以形成一個節點的電導矩陣,然后顯示出該節點的電導矩陣。通過電導矩陣和功率方程,可以將原始的問題轉化成對于非線性問題的求解,可以采用牛頓拉夫遜高斯方法,即通過每一節點的斜率作切線與橫軸相交的點,所對應的縱坐標為下一個球節點,通過一次又一次的迭代更新,分別在每一次迭代過程中形成初始值,將初始值代入功率方程進行不斷修正,經過三次到四次便可以得到所需要的求解值。 設節點總數為n,PV節點數為r,則潮流應包含n-1個有功方程和n-r-1個無功方程。 牛頓法的修正方程式為: (1-6) 設n維非線性方程組為 (1-7) 求解得到修正量,并對各變量修正得 (1-8) 很容易看到,修改后的雅可比矩陣方程的系數矩陣具有以下特點: 1)相量矩陣為矢量矩陣; 2)求解矩陣具有不對稱性; 3)雅可比矩陣在拓撲學意義上具有稀疏性。 牛頓法的圖形解釋如圖1所示。 圖1 牛頓拉夫孫法圖形解釋 現在把牛頓法推廣到多變量非線性方程組的情況。設有變量的非線性聯立方程組: (1-9) (1-10) 一般第k次迭代時的修正方程式為: (1-11) 上式可以簡寫為:F(X(k))=J(k)ΔX(k)。 從幾何意義上說,牛頓法就是切線法,是一種逐漸線性化的方法。 MATLAB起源于美國科學家Cleve Moler博士在線性代數教學領域的早期工作。當他在新墨西哥大學教授線性代數課程時,他構想并開發了MATLAB軟件,并在20世紀80年代早期由Mathworks公司銷售。它的出現開創了科學計算的新時代。它是由Math Works開發的一款商用數學軟件,Math Works是一種用于算法開發、數據可視化、數據分析和數值計算的高級技術計算語言和交互環境,主要包括MATLAB和Simulink。 MATLAB腳本節點是實現試驗室視圖和MATLAB之間互聯的橋梁。它是通過一個嵌入式的Active X控件通過Lab VIEW安裝的,與MATLAB服務器建立連接,與數據交互,通過調用命令和函數實現復雜而龐大的數值計算。MATLAB分析過程,使用MATLAB腳本節點的方法如下:在虛擬儀器功能面板,選擇數學>腳本和公式>腳本節點>MATLAB腳本,您可以添加一個MATLAB腳本節點的流程圖的左派和右派MATLAB腳本節點的各種類型的輸入或輸出參數可以單獨添加相應的配置。 MATLAB的功率分布編程過程是這樣的,首先在你點擊開始運行按鈕時,你所編寫的程序以字符轉換的形式轉換成為一系列的字符串,通過字符串發送給腳本文件進行執行腳本文件,通過所規定的算法和計算流程求解非線性方程來計算每一個節點的有功功率、無功功率和電壓相角等,耗時的計算和其它輸出功率流分布條件和數據分析。vi對節點的輸出參數進行處理,并在軟件操作界面中顯示。計算完成后,將出現計算完成對話框,同時使用Unset Busy.vi移動鼠標指針。未配置為忙。當需要保存計算結果時,單擊save data按鈕,程序將計算結果保存為Excel文件。 為了保障在MATLAB環境下系統能夠保持較高的計算速度,可以對計算方程進行矢量化。這樣可以是計算過程更加簡單,并且程序編寫也比較方便。以PQ分解法為核心的潮流計算方程如下式所示: (3-1) 式中Pi,Qi,Gij,Bij,δij分別為節點i處的有功,無功,電壓幅值,i、j節點間導納矩陣實部、虛部,i、j節點間相角差。修正方程表示為: (3-2) (3-3) 在這種潮流計算過程中,通過對矩陣的虛部進行計算,得到B′。B′在矩陣中的節點元素為0,對角元一般情況為1;方程中的B″則為矩陣的平衡節點,其對角元同樣為1,行和列元素為0。方程在n×n對稱矩陣中,同時將ΔP和ΔQ進行同樣的運算和處理。 ΔP和ΔQ為列向量,ΔP將平衡節點對應行置0,ΔQ則將平衡節點和PV節點對應行置0。由于節點功率可表示為: Si=Pi+jQi (3-4) 取上式實部和虛部即可方便的得到ΔPi,ΔQi, 則(3-1)式可以矢量化表示為: S=V*(Y*V) (3-5) ΔP=P-Re(S) (3-6) ΔQ=Q-Im(S) (3-7) 其中:.*表示向量與向量間對應元素相乘;Y,V分別表示導納矩陣、電壓矢量的共軛;S代表節點功率。MATLAB代碼如下: S=V.*(conj(Y*V)) dP=P-real(S) dQ=Q-imag(S) 通過MATLAB代碼我們也不難發現,其與潮流計算的形式十分類似,這樣的編寫形式能夠有效的提高編碼的編寫速度,并且符合程序的計算效率。 利用MATLAB Script節點,使用PQ速解法求解電力系統潮流分布的MATLAB程序流程圖見圖2。 圖2 基于MATLAB的求解流程 電力系統潮流計算方法經過不斷改進,正在逐步改進。每種方法都有其各自的應用領域和缺點。對于不同的情況,我們必須選擇合適的方法或者結合多種方法來更好的解決問題。當然,在實際應用中也會出現計算結果不收斂的情況。功率通量計算的求解方法還需要進一步的研究和改進。本文通過推導一個公式,可以根據目標對象的基數方程對迭代公式進行設置和更新,從而避免了復雜的微分過程,得到了一個適合于編制MATLAB程序的迭代公式。潮流計算是電力系統分析中最基本的電氣計算方法之一。本文編寫了一個基于PQ分解法的潮流計算程序,討論了如何利用MATLAB指令的功能快速創建迭代公式,進一步提高程序開發效率。最后給出了MATLAB的設計思想和方法。 本文研究中受到時間和精力限制,僅僅將PQ分解法利用MATLAB技術進行仿真實現,未能對牛頓-拉夫遜以及高斯-賽德爾兩種算法進行研究和實現MATLAB程序的編寫,在以后研究中,要對這三種算法下的程序進行設計與實現,并對比三種算法下的計算結果,得出最優的潮流計算方式,為電力系統的維護提供支持。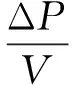
2.3 牛頓-拉夫遜原理
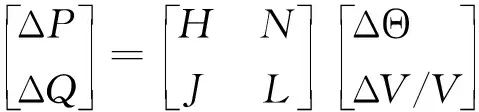
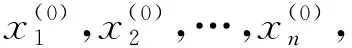
3 基于Matlab的潮流計算程序設計
3.1 MATLAB簡介
3.2 MATLAB Script節點技術
3.3 MATLAB編程實例
3.4 潮流公式矢量化
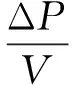
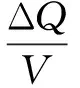
3.5 MATLAB編程算法
4 結 語

