點吸收式波浪能摩擦納米發電系統輸出性能的仿真研究

張 迪，林忠華,3*，楊紹輝,2,3，李 暉,2,3，蔣清山,3，肖國紅,3

（1. 集美大學 機械與能源工程學院，福建 廈門 361021；2. 福建省能源清潔利用與開發重點實驗室，福建 廈門 361021；3. 海洋可再生能源裝備福建省高校重點實驗室，福建 廈門 361021）

隨著全球化石能源的日益消耗，尋求新的能源獲取方式成為人們關注的焦點。傳統方式獲取機械能轉化為電能得到了飛速發展，但是波浪能發電技術卻發展緩慢[1]。波浪能開發利用方法根據收集原理可分為：點吸收式（振蕩浮子式）、筏式、振蕩水柱式、越浪式、擺式、點頭鴨式等[2]。目前國內研制的點吸收式波浪能發電裝置有：中山大學利用齒輪齒條傳動研制的一種點吸收波浪能發電裝置，山東大學研制的120 kW“山大一號”，中科院廣州能源所研制的岸式振蕩浮子發電站，中國海洋大學研制的10 kW組合型振蕩浮子波浪能發電裝置，浙江海洋大學研制的“海院一號”，集美大學發電研制的“集大一號”波浪能發電平臺，以及在“集大一號”平臺基礎上改進的，利用液壓系統進行能量傳遞的“集大二號”和新建造的半潛式“集大三號”波浪能發電平臺。國外點吸收式波浪能發電裝置主要有加拿大Finavera公司按照陣列布置設計并建成的42座Aqwa Buoy波浪能裝置，愛爾蘭研制的Wavebob裝置，美國俄勒岡州立大學研制的10 kW點吸收波浪能發電裝置，英國的阿基米德波浪擺（AWS）和丹麥的Wave Star陣列式波浪能發電裝置等[3-5]。波浪能轉換傳遞方式有機械齒輪式、液壓式、直線電機式和磁流體式等，上述能量轉換裝置結構的復雜性大大限制了波浪能裝置的小型化和微型化發展。2012年，王中林院士提出了一種新型發電方式——摩擦納米發電機（TENGs），相比于傳統的機械能捕獲方式，摩擦納米發電機具有結構簡單、成本低、綠色無污染、輸出電壓高等特點。另外，摩擦納米發電機是基于摩擦生電和靜電感應相結合的原理將機械能轉化為電能的新型發電方式，可有效地將波浪能轉化為電能[6-7]。

本文提出了一種基于點吸收的波浪能摩擦納米發電系統，該系統由振蕩浮子、具有納米摩擦層的連桿套筒和固定在海底的支架組成。摩擦納米發電機采用垂直滑動模式，其兩個摩擦層采用聚二甲基硅氧烷（PDMS）薄膜和鋁(Al)作為接觸摩擦的材料，并利用仿真模型分析了垂直滑動摩擦模式摩擦納米發電機（TENGs）的電能輸出特性，為該裝置的造波水槽實驗和實海況海試提供理論基礎。

1 理論模型

1.1 系統的結構介紹及工作原理

本文提出的理想模型是利用波浪能進行摩擦發電。如圖1 (a)所示，外部有4根腳架作為支撐固定到海底，采用垂直滑動摩擦方式進行發電，它采用套筒式連桿，上部較粗的套筒固定在上平板，下部較細的連桿連接浮子。在較細的連桿外壁先涂一層絕緣材料，然后在絕緣材料上鍍一層光滑的Al電極，在較粗的連桿內側也是先涂一層絕緣材料，再在絕緣材料上鍍一層光滑的石墨電極，最后在Al電極表面黏貼一層PDMS薄膜，再用導線把兩個Al電極連接到負載。在此裝置中Al電極不但作為電路電極，也作為摩擦層。圖1 (b)為裝置的三維圖。

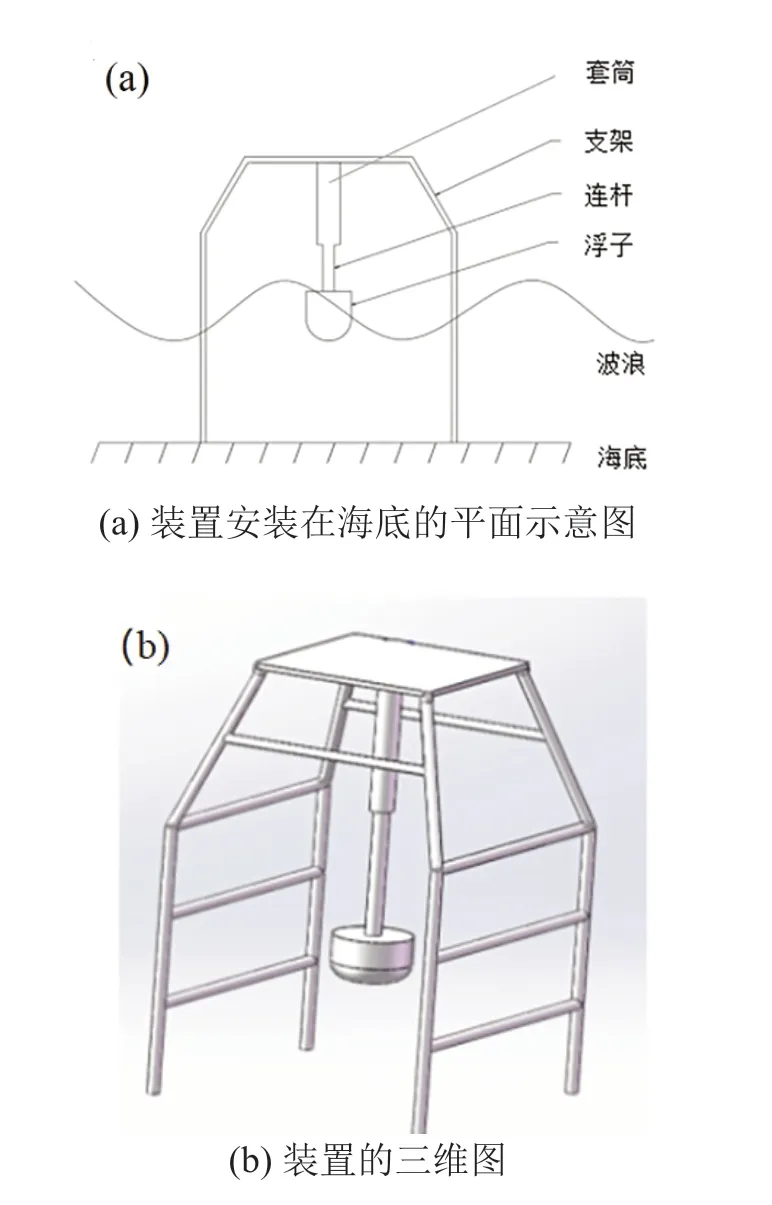
圖1 點吸收式波浪能摩擦納米發電機

該裝置通過腳架固定在海底，浮子受到波浪的作用進行上下振蕩，從而帶動連桿運動，浮子靜止在水面時套筒內的兩個摩擦層是重合的，如圖2(a)所示連桿上的電極1（Al電極）會在套筒內部的介電層（PDMS薄膜）進行往復性摩擦。如圖2(b)所示設極板和介電層在垂直方向長度均為l，垂直方向分離的距離為x，介電層的厚度為d。當浮子在波浪作用下向上運動時，電極1與介電層分離時，由于摩擦生電，在介電層分離區域的表面均勻分布著電荷密度為-σ的摩擦電荷，而電極1表面分布著極性相反且等量的電荷，因此在開路狀態下，電極2（石墨電極）的電荷總量為0，隨著浮子向上運動摩擦距離增大，電極1需要更多的正電荷來平衡接觸電場，所以當用導線連接外部負載電路時，電子會由電極1流向電極2，產生電流對外做功。當浮子往上運動到最頂點時，此時兩個電極的電勢差最大，電極1聚集的正電荷達到最大值，浮子從位移的最頂點慢慢往下運動時，摩擦層之間的接觸面積增大，電極1上聚集多余的正電荷，此時電子會從電極2流向電極1，兩個摩擦層重合時，電勢差為0。浮子繼續向下運動，由于摩擦發電只與摩擦的距離大小有關，所以以摩擦層重合時為對稱點，電極1向上運動和向下運動摩擦發電的情況是一樣的。

圖2 摩擦納米發電機內部構造圖

1.2 點吸收式波浪能振蕩理論

假設流體為理想不可壓縮的無粘性流體，當浮子振動時波浪運動無旋，如圖3所示H(t)為浮子重心的位移；h0為浮子在靜水平面以下的高度，浮子在波浪作用下上下振動，波浪假定為規則波，波浪的波面方程為：

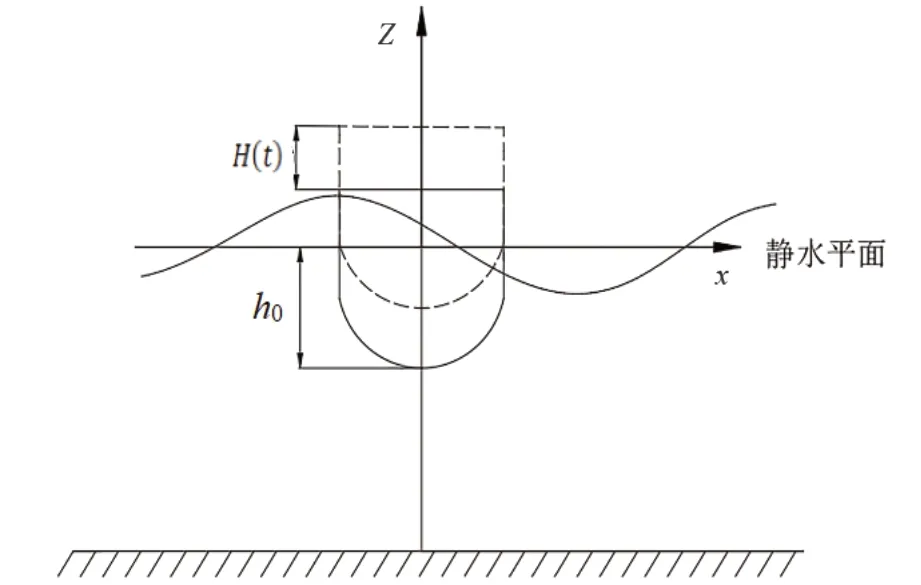
圖3 浮子升降示意圖

式中：A為波浪振幅；ω為波浪圓頻率，當浮子的直徑遠小于波浪長度L時，浮子對波浪場的運動形式的影響可以忽略不計，根據線性波理論，速度勢函數φ可以表示為[8]：

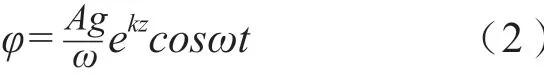
式中：k為波數，波傳播一個波長，水質點振蕩一周g為重力加速度。根據牛頓第二定律可得浮子的運動方程可以表示為[9]：

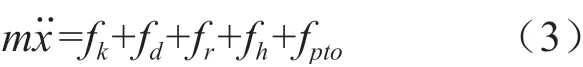
式中：m為浮子的質量；為浮子在垂直方向的運動加速度；fk為弗洛德-克雷洛夫力，即波浪入射力；fd為繞射力；其中入射力fk加繞射力fd等于波浪激勵力fe；fr為輻射力；fh為靜水恢復力；fpto是能量輸出裝置（PTO）產生作用于浮子的垂直負載。

在規則波中，波浪激勵力可以表示為：

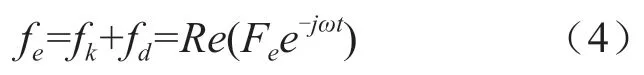
式中：Re表示取其實部，設{x,fe}=Re({X,Fe}e-jωt)，X、Fe為位移和波浪激勵力的復數模，由于浮子在X軸方向的尺寸遠小于入射波的寬度，根據文獻[10]Fe為波浪激勵力的振幅可大致表示為：

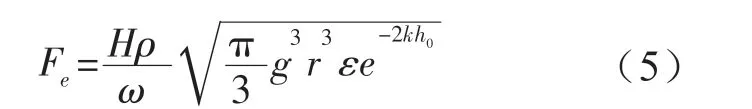
式中：H為自由波面高度；ρ為水的密度；ε為阻尼系數，r為浮子的半徑。

輻射力fr與浮子的運動加速度和速度有關，因此可以表示為：

式中：B是浮子在流體中由于運動而使得周圍流體一起運動產生的附加質量；C是關于波浪頻率的輻射阻尼系數；，分別為浮子在垂直方向的速度和加速度。輻射阻尼系數可近似表示為[10-11]：

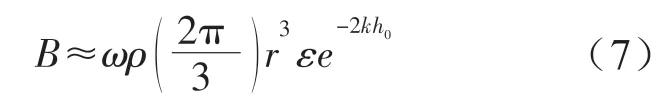
靜水恢復力fh是浮子排開液體的重量與自身重量之差，可以表示為：

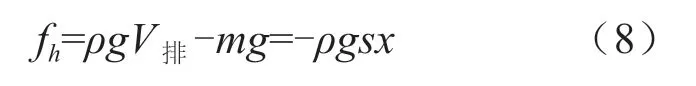
式中：V排為浮子排開液體的體積；s為浮子吃水線處的浮子截面面積。

由于本文所提出的點吸收式摩擦納米發電機能量輸出裝置（PTO）沒有液壓油缸等結構，只有摩擦層之間的摩擦力，所以fpto=–μN，μ為PDMS摩擦層的摩擦系數；N為PDMS摩擦層與套筒內側電極之間的正壓力。所以由公式（3）得：

由于套筒和連桿的尺寸是固定的，連桿外側的PDMS介電層和套筒內部的電極1之間處于剛好接觸到間隙配合之間，它們之間的正壓力N接近于0，所以PDMS介電層與電極1之間的摩擦力可以忽略不計。運動時電極之間產生電場，PDMS介電層隨著電極2一起運動，在電場作用下它靠近電極兩側會分布等量的異性電荷，其整體處于靜電屏蔽狀態，且不切割磁感線，即不會產生電磁阻尼力，所以浮子在垂直方向運動近似看作自由振蕩。所以公式（9）可以寫成：

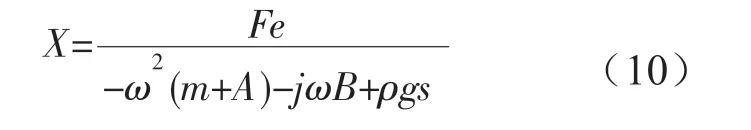
從式（10）可以看出浮子在垂直方向的自由振蕩與波浪激勵力、波浪頻率、浮子質量、附加質量、輻射阻尼系數、浮子吃水線處截面面積等有關。Jeffery基于傅里葉變換對波浪能發電裝置的浮子振蕩情況進行了時域分析，其運動方程為：

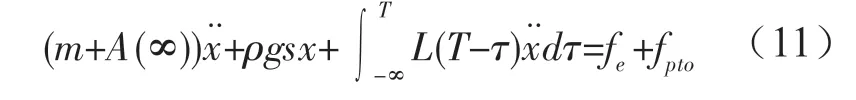
1.3 滑動式摩擦納米發電機理論

在推導垂直滑動模式TENGs的理論表達式時，考慮到實際情況l（極板和介電層長度）總是比d（介電層厚度）的數量級大得多，況且當兩個摩擦層完全分離后很難回到原來的狀態而不損壞介電層，所以在實際應用中垂直分離的距離x要小于等于0.9l，使得兩個介電層有個重疊區域，便于下次的往返運動；介電層的厚度與其長度相比小得多，只要兩個摩擦層沒有完全分離，總電容就由重疊部分區域的電容決定，設定d0為有效厚度常數，為相對介電常數，電容C的表達式為：

這里的ε0為空氣介電常數；w為PDMS介電層的寬度；x為電極1的位移也就是浮子的位移，取向上運動為正，向下為負，系統的摩擦發電只與電極1位移的大小|x|有關，與位移的方向無關。

如圖2(b)所示，對于電極2未重疊區域電荷密度為：

式中：σ代指電荷密度的數值。

對于電極2重疊區域電荷密度為：

對于電極1未重疊區域電荷密度為：

對于電極1重疊區域電荷密度為：

根據上面的式子可以推導出開路電壓Voc的表達式為：

短路時轉移電荷量為：

短路電流為：

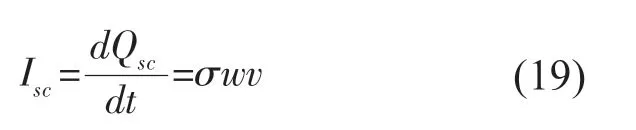
式中：v是|x|對時間t的導數。

連桿套筒之間的滑動摩擦是利用波浪的上下振動，設定波浪頻率為0.2 Hz，波浪高度分別為0.3 m、0.35 m、0.4 m、0.45 m、0.5 m，利用水動力軟件AQWA對浮子的上下振動位移進行仿真，為了確保仿真的可靠性，垂直分離的距離x的絕對值要小于等于0.9l。

2 仿真分析

2.1 點吸收波浪能裝置的振蕩仿真分析

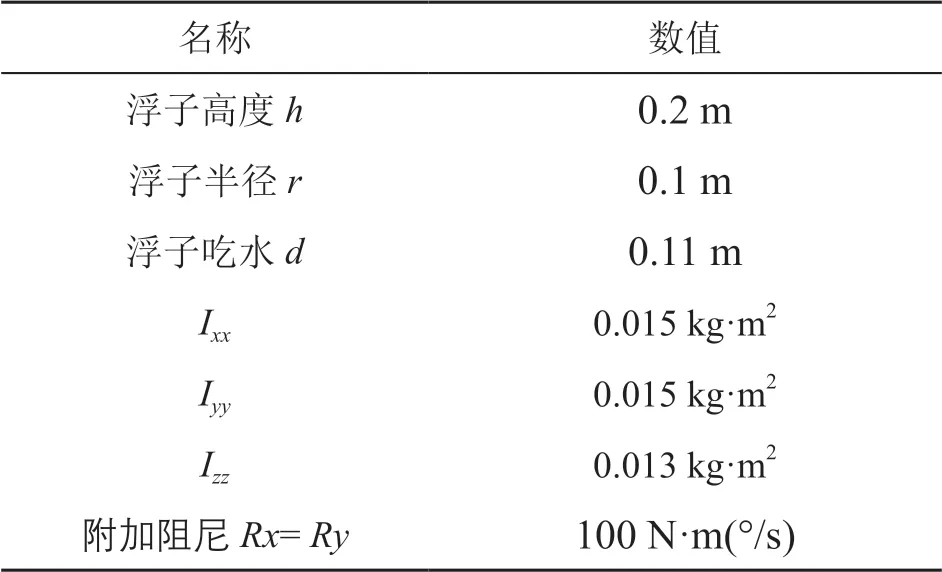
表1 用于浮子位移仿真的主要參數

對點吸收裝置進行簡化建模，只保留了浮子部分，浮子在z軸方向上下振動，浮子本身的質量為2.85 kg，浮子表面會受到入射波的影響，在浮子表面的壓強分布不一樣，如果沒有約束的話，浮子會產生翻滾現象，本文仿真只要求在垂直方向運動，所以在X軸設置旋轉的附加阻尼Rx=100 N·m(°/s)，在Y軸方向同樣設置旋轉阻尼Ry=100 N·m(°/s)，來防止浮子發生翻滾；由于能量輸出裝置（PTO）的摩擦阻力非常小，所以在垂直方向的PTO阻尼設置為0。具體建模過程如下。

（1）利用SolidWorks進行浮子的三維建模，并把模型轉化成XT格式；然后打開ANSYS中的workbench界面；（2）把建好的模型導入Design Modeler，按照吃水線把模型分割成兩部分，再進行抽殼，厚度設為0；（3）設置海域面積為S=100 m×100 m，水深15 m，重力加速度9.8 m/s2，浮子吃水深度0.11 m，計算浮子中心，設置中心位置；（4）設置附加阻尼Ry=Rx=100 Nm(/s)；（5）對浮子進行網格劃分，設置最大網格尺寸為0.01 m，最小繞射單元網格尺寸為0.004 m；（6）將AQWA頻域計算部分的波浪頻率設為100份，時域計算部分的規則波波高0.5 m，波浪周期5 s，計算時長為60 s，步長為0.05，波浪入射方向與x軸呈180°。

圖4所示為波浪頻率0.2 Hz時，不同波浪高度下的浮子位移，是以浮子重心為位移0點，向上位移為正，向下位移為負，由于是浮子的上下振動使得套筒內的摩擦層進行上下往復摩擦，所以下文中的摩擦位移與浮子位移是一致的。

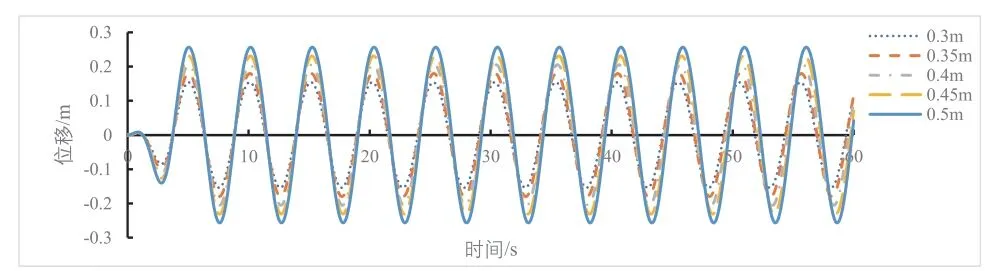
圖4 波浪頻率0.2 Hz，不同波浪高度下浮子的位移

2.2 不同波浪高度下TENGs輸出特性的仿真分析

將AQWA仿真得到的浮子位移數據導入數學仿真模型中，然后對摩擦納米發電機TENGs的輸出性能進行仿真分析，表2為摩擦納米發電機仿真時的具體參數。

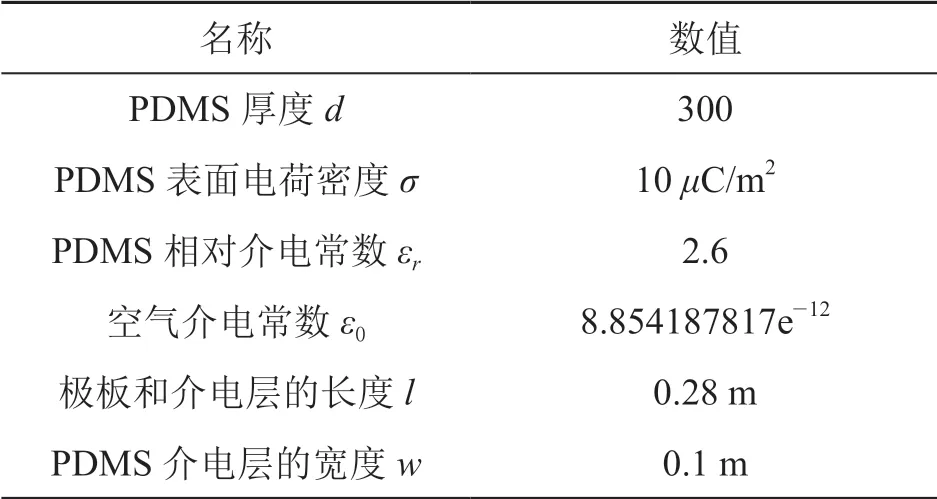
表2 摩擦納米發電機用于仿真時的各項參數[12]

浮子的上下振蕩情況就是摩擦納米發電機PDMS介電層和Al電極的相對運動情況，仿真分析結果顯示，不同波浪高度下的開路電壓、轉移電荷量、電容和短路電流的變化與絕對摩擦位移|x|的大小有對應，波浪高度影響到絕對摩擦位移|x|的最大值，當不同波浪高度下的絕對摩擦位移|x|相等時，開路電壓、轉移電荷量、電容和短路電流是一樣的，在圖5至圖7中，波浪高度0.3 m的數據會依次被波浪高度0.35 m、0.4 m、0.45 m、0.5 m的數據所覆蓋。根據開路電壓公式求得開路電壓與位移的關系，摩擦位移x有正有負，但是摩擦層只要有相對位移就能產生電壓，摩擦位移x向上為正，向下為負，當摩擦位移x值為正時，摩擦位移x從0到最大值（最高點）時，電極1需要更多的正電荷來平衡接觸電場，電流從電極2流向電極1。摩擦位移x從最大值（最高點）返回到0時，電極2的電勢高于電極1的電勢，電流從電極1流向電極2，當摩擦位移x為負時，發電情況和摩擦位移x為正時一樣，只與絕對摩擦位移|x|有關，從圖5可以看出絕對摩擦位移|x|值越大，相應的開路電壓越大。不同波浪高度下，只要絕對摩擦位移|x|相同，產生的開路電壓就相同，從圖2上解釋為電極1和PDMS介電層重疊的部分越小對應的開路電壓越大，且波浪高度越大，最大開路電壓也越大。從圖6可以看出波浪高度0.5 m時短路時轉移電荷量與位移呈正比關系，只要絕對摩擦位移|x|相同，轉移電荷量就相同，絕對摩擦位移|x|值越大，轉移的電荷量也就越大，且波浪高度越大，最大轉移電荷量也越大。圖7顯示電容隨絕對摩擦位移|x|變大而減小，位移為0時，也就是電極1與PDMS介電層完全重合時電容最大，最大為2.09 nF。從圖8可以看出浮子運動規律后，短路電流隨位移x的變化呈封閉曲線，在封閉曲線的內部是浮子從剛開始運動到還未達到穩定的周期性運動期間短路電流的變化，圖8的曲線對應的振蕩摩擦發電的順序是從坐標軸原點開始向外做順時針旋轉，波浪高度越大，浮子振蕩穩定后封閉曲線所包圍的面積越大，同樣在浮子振蕩穩定后，摩擦位移為0時，短路電流最大，摩擦位移達到波浪最大振幅時，短路電流為0。圖9(a)為浮子在振蕩穩定前的短路電流隨摩擦位移的變化情況，圖9(b)為浮子振蕩穩定后短路電流隨摩擦位移的變化情況。

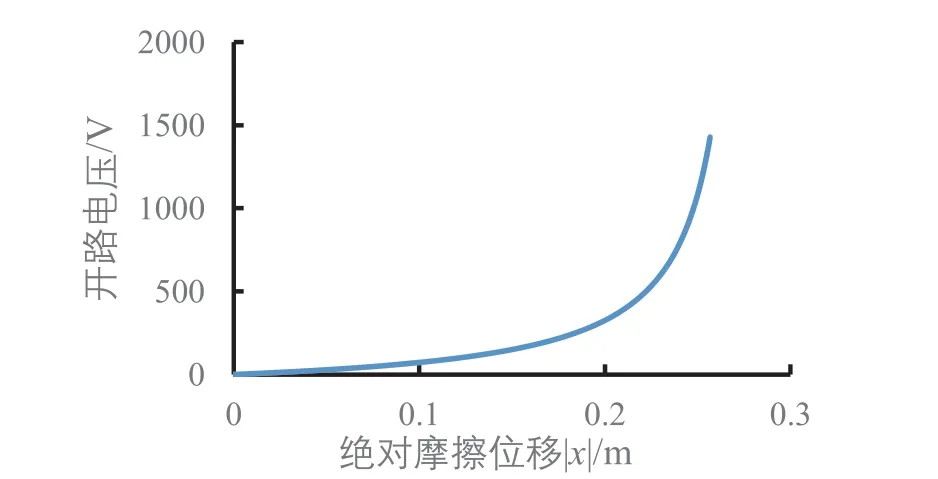
圖5 波浪高度0.5 m下開路電壓隨摩擦位移的變化

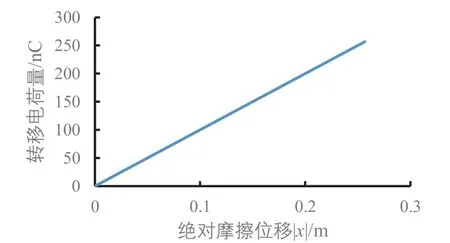
圖6 波浪高度0.5 m下短路時轉移電荷隨摩擦位移的變化

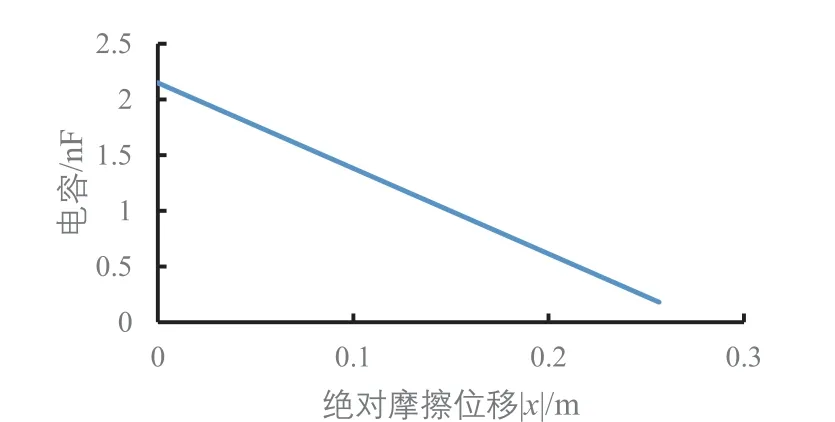
圖7 波浪高度0.5m下TENGs的電容隨摩擦位移的變化

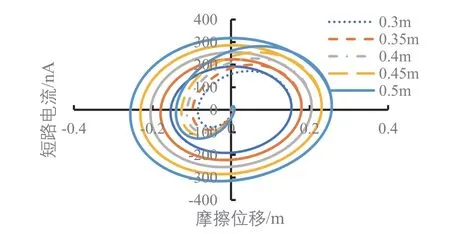
圖8 不同波浪高度下短路電流隨摩擦位移的變化

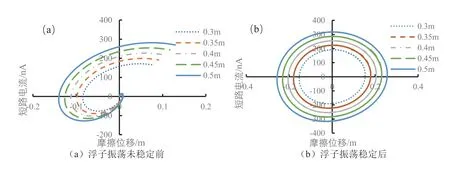
圖9 不同波浪高度下浮子振蕩的短路電流隨摩擦位移的變化情況

本文研究在波浪頻率為0.2 Hz、不同波浪高度下TENGs的輸出特性的隨時間的變化規律，從圖10可以看出，隨著波浪高度的增加，開路電壓也隨之增大，并且當浮子運動規律后，電壓輸出也呈現規律變化，并且頻率變為0.4 Hz，周期為2.5 s，是波浪周期的一半，原因是電極1與PDMS介電層重疊部分是l-|x|。圖10可以看出在波浪高度為0.3 m的基礎上每增加0.05 m，電壓輸出穩定后最大開路電壓增加量也會隨著波浪高度的增加而增加。圖11曲線對時間的導數就是圖12，轉移電荷量和短路電流都隨著波浪高度的增加而增加，它們的周期也和開路電壓一樣為2.5 s。圖13為不同波浪高度下電容隨時間的變化情況，可以看出在0～3 s內電容值曲線與后面的曲線不同，是因為浮子受自身慣性影響，還未達到規律的運動，浮子達到規律的運動后電容曲線也呈規律的周期變化。最大電容值不隨波浪高度的變化而變化，最大電容為電極1與PDMS介電層完全重合時，最大為2.09 nF，最小電容隨著波浪高度的增加而減小，是因為波浪高度增加電極1與PDMS介電層最大重疊距離l－|x|減小，所以最小電容減小。

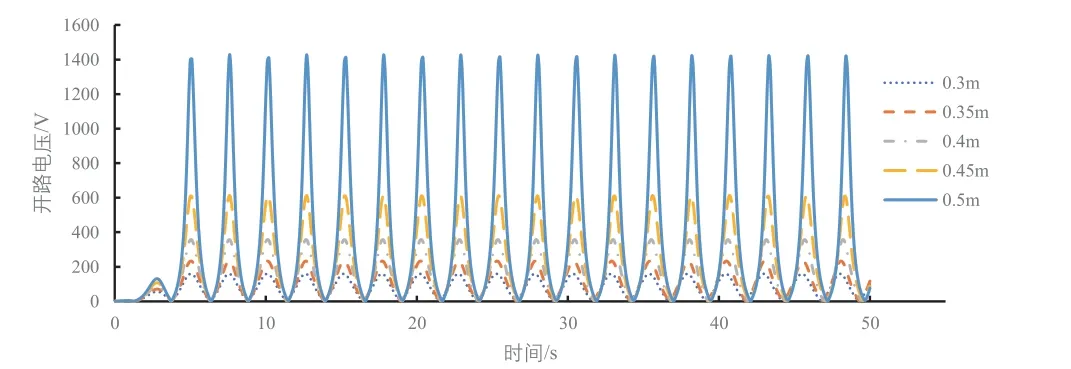
圖10 不同波浪高度下的開路電壓

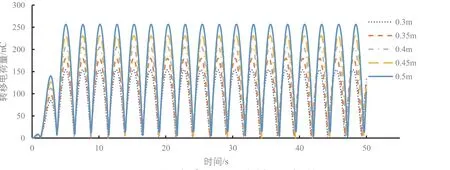
圖11 不同波浪高度下的轉移電荷量

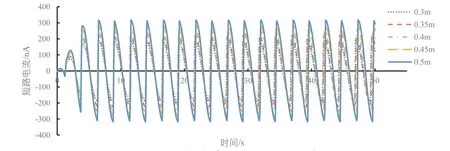
圖12 不同波浪高度下的短路電流

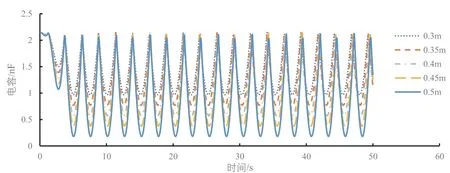
圖13 不同波浪高度下的電容

圖14至圖17是對圖10至圖13的圖形特征做了進一步分析。圖14顯示波浪高度增加時最大開路電壓呈拋物線趨勢增大。圖15和圖16規律一樣，最大轉移電荷量和最大短路電流隨波浪高度的增加基本呈線性增加。圖17直觀地顯示了最小電容隨波浪高度的增加呈線性減小。

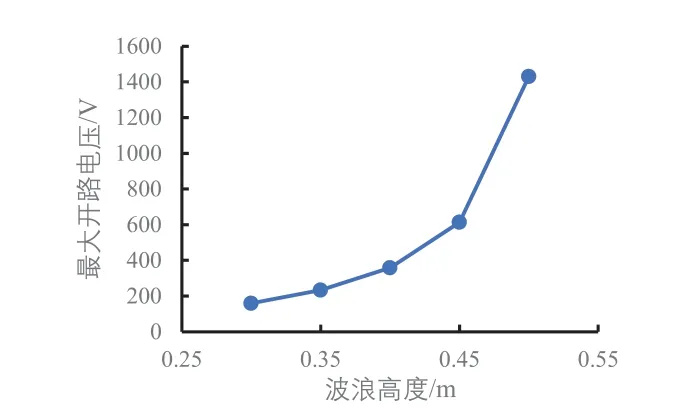
圖14 不同波浪高度下的最大開路電壓

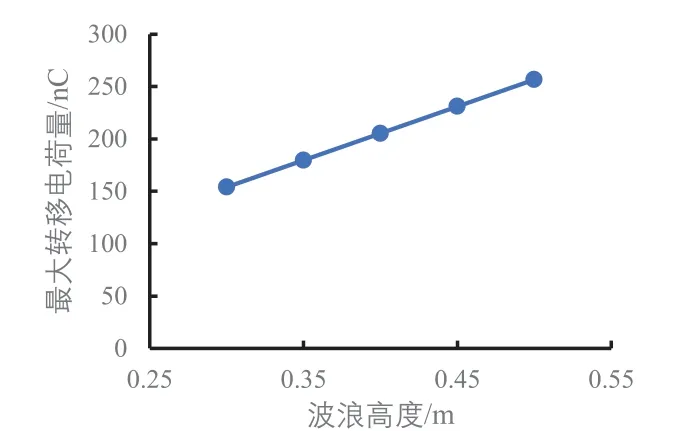
圖15 不同波浪高度下的最大轉移電荷量

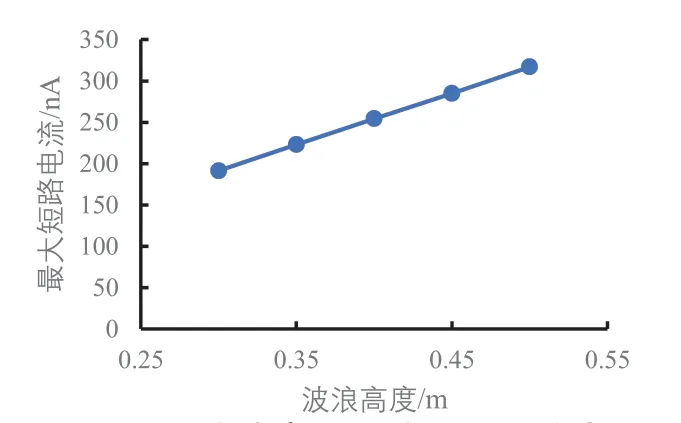
圖16 不同波浪高度下的最大短路電流

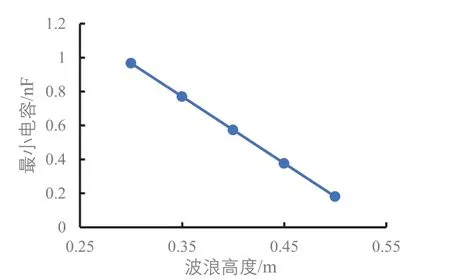
圖17 不同波浪高度下的最小電容

圖18為不同波浪高度下摩擦納米發電機在不同外接負載下峰值電壓和在峰值電壓下對應的功率與電流，從圖可以看出功率會隨著負載電阻的變化而變化，在109Ω附近會出現最大功率，并且功率曲線會隨著波浪高度的增加而變大。負載兩端會產生隨時間變化的電壓，最大電壓即峰值電壓會隨著負載的變大而逐漸變大，并且波浪高度的增加也會引起峰值電壓的變大。電流在數值上等于功率與峰值電壓的比值，電流整體是隨著負載阻值的增加呈下降趨勢，并且波浪高度對負載電流的影響不大。

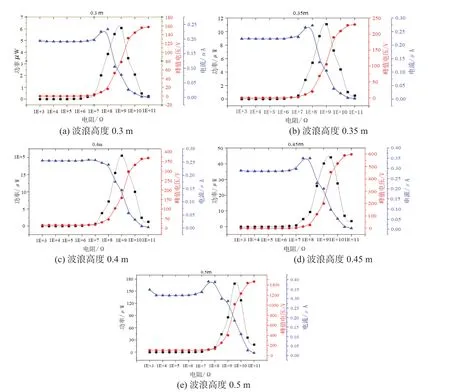
圖18 不同波浪高度下電能輸出特性隨負載阻值的變化

3 結 論

本文提出了一種點吸收式波浪能摩擦納米發電裝置，該裝置利用波浪驅動浮子進行上下振蕩，從而帶動連桿套筒內的納米摩擦發電機進行摩擦發電，通過對點吸收式摩擦納米發電機進行仿真分析，改變波浪高度和外接負載的阻值研究其電能輸出特性，研究結果表明。

（1）電能輸出穩定后，電容隨著絕對摩擦位移|x|的增加呈線性減小，轉移電荷量隨著絕對摩擦位移|x|的增加呈線性增加，而開路電壓隨絕對摩擦位移|x|的增加呈現拋物線似的增加。

（2）在波浪高度增加時，電能輸出穩定后開路電壓、短路電流和轉移電荷量也會相應增加，最大開路電壓增加量也會呈拋物線趨勢增加，最大轉移電荷量和最大短路電流隨波浪高度的增加基本呈線性增加。

（3）在波浪高度增加時，電能輸出穩定后電容的最大值不會隨波浪高度的變化而變化，最小電容隨著波浪高度的增加而呈線性減小。

（4）電能輸出穩定后，開路電壓、短路電流、轉移電荷量和電容的曲線周期變為波浪周期的1/2。

（5）負載兩端的功率和電壓會隨著波浪高度的增加而增加，并且負載兩端的峰值電壓隨阻值的增加而變大，功率會隨阻值的增加出現一個峰值，其最佳匹配電阻在109Ω左右，此時摩擦納米發電機的發電性能最佳，對應波浪高度為0.5 m時最大發電功率為173.6μW。

本文對點吸收式波浪能摩擦納米發電裝置進行了理論仿真研究，為下一步實驗提供了理論支持。摩擦納米發電機的材料屬性和裝置的防水性能是制約裝置發電因素，將是未來研究的方向之一。