基于風險及模式識別的電力系統支路重要性評估

趙一婕，辛 巍，范 楊，程 繩

（1.航宇救生裝備有限公司武漢創新中心，湖北 武漢 430000；2.國網湖北省電力有限公司檢修公司，湖北 武漢 430050）

0 引言

近年來，全球性極端自然災害不斷發生，可能導致電力系統出現從局部到大面積的停電事故［1-7］，嚴重威脅電網的安全運行。因此，國內外學術及工程界提出采用差異化規劃方法［8-9］構建核心骨干網架，以應對嚴重自然災害，保障重要負荷持續供電。電網核心骨干網架［10-11］構建的關鍵在于對網架支路的重要性進行評估、選擇與排序。文獻［12］提出了一種基于小世界拓撲模型的電網脆弱性評估方法，該方法側重于從網絡拓撲建模和網絡基本特征方面來尋找重要線路，但沒有從電網運行特性及約束條件方面考慮線路重要性。文獻［13］提出了一種基于電網生存性評估的關鍵線路識別方法，該方法采用平均最短電氣距離反映線路的重要性，融入了電氣元件的參數特征，但是很難考慮了拓撲結構變化的概率。文獻［14］提出了一種電力系統脆弱性的風險評估方法，該方法兼顧了事故概率以及事故后對整個電力系統的嚴重后果，對支路的重要性評估具有一定的啟發意義。

在電力系統風險評估領域，多風險指標的綜合方法一般采用加權形式，各種加權方法的區別主要在于各指標權重的確定［15-22］。文獻［23］中利用層次分析法再結合專家調查法實現指標權重的分配，該方法有很強的解釋性，但操作起來復雜。文獻［24］中暫態安全風險的綜合指標采用了范數加權的綜合方法，該方法的權重系數受主觀因素影響較大。目前，對于支路安全分級問題的研究還不夠深入，文獻［25］中將電壓安全分為5個等級，分級原則是根據風險計算指標值來人為均勻設定每一級的風險分類區間。這種分級方法簡單方便，但必須依托于綜合風險值的基礎之上，并且主觀性強。因此，需要尋找一種客觀的權重確定方法和新的分級方法，該分級方法能獨立于綜合風險值，并且能與綜合風險計算結果相一致。

本文提出了一種電力系統支路重要性排序和分級的新思路。設定事故集為單一支路退運，得到過負荷風險、低電壓風險和失負荷風險，并構成三維風險向量；采用迭代自組織數據分析算法（Iterative Selforganizing Data Analysis Techniques Algorithm，即ISODATA）將三維風險向量按照數據相似度聚類，實現每條支路風險等級初步自動評定；使用主成分分析方法對三維風險指標進行分析，將其投影到主方向軸線上就可以獲取能夠清晰分辨不同重要性等級的一維數據，完成綜合風險指標計算，對支路重要性進行排序，并將分級與排序結果進行對比，完善支路分級結果。本文從支路退運風險角度出發，提出了支路重要性評估的新方法，為核心骨干網架的構建奠定了理論基礎。

1 基于退運風險自組織的支路重要性分級

1.1 支路退運風險指標

定義電力系統的支路退運風險為支路退運的概率與退運后產生的后果的乘積，即：

式（1）中，P(Ei)是支路i退運的概率，一般服從泊松分布；f(Y|Ei，L)是支路退運后系統處于特定運行狀態的概率分布；Sev(Y)描述了在狀態Y時事故的嚴重度。

支路退運風險考慮了單一支路退運的概率，以及該支路退運后對整個系統中其他所有元件所造成的后果，以下3種指標可以分別從不同的角度比較科學全面地評估該支路在整個系統中的重要性。

1）過負荷風險

過負荷風險是電力系統事故后，導致其他未故障支路的有功功率超過其額定值的可能性和嚴重程度的結合，即：

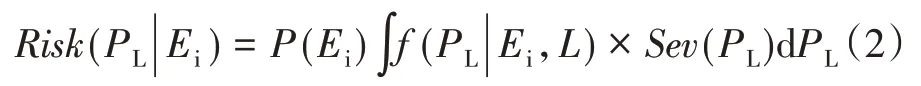
其中，過負荷嚴重度取決于事故后其他所有支路的潮流分布，嚴重度函數如式（3）所示，曲線如圖1所示。

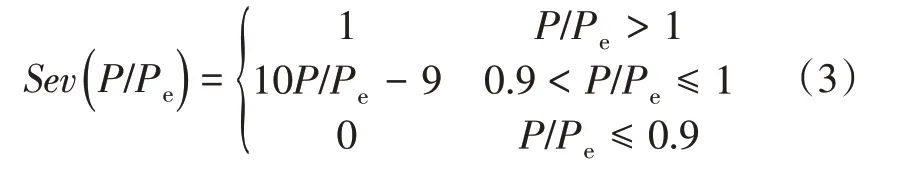
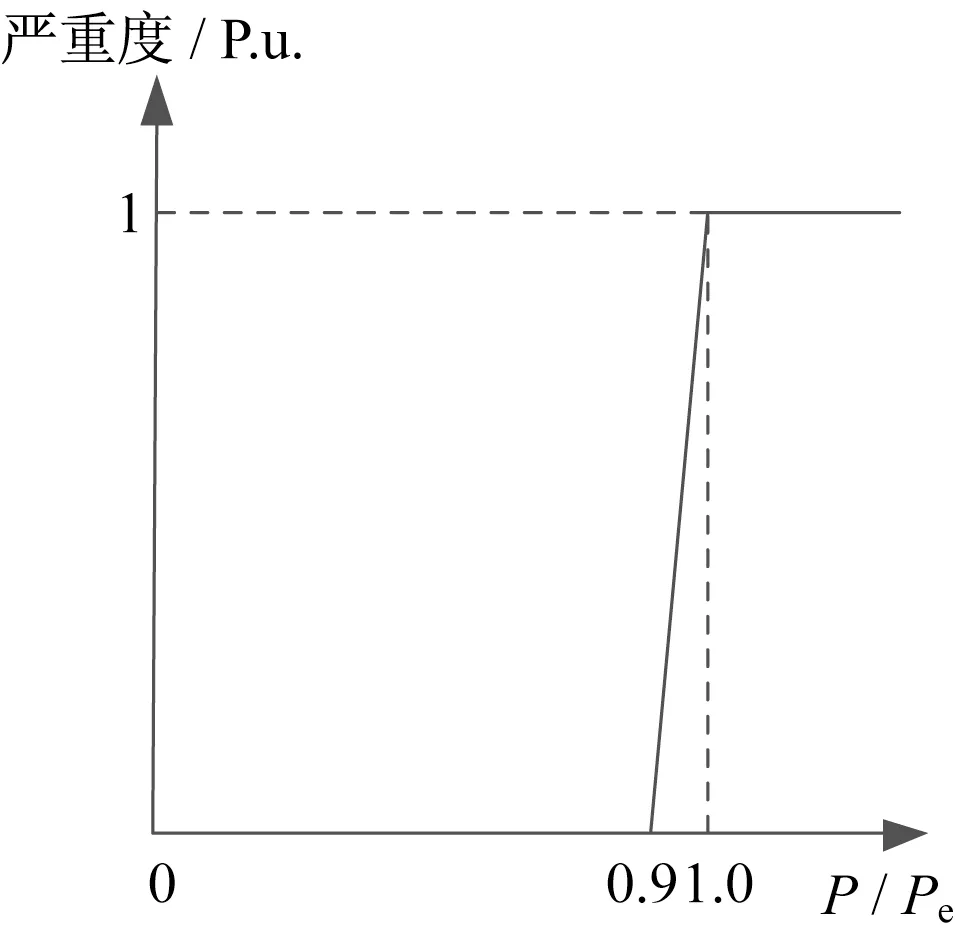
圖1 過負荷嚴重度函數Fig.1 Severity function of overload risk

2）低電壓風險

低電壓風險是電力系統事故后導致系統中節點電壓低于額定值的可能性和嚴重性的結合，即：

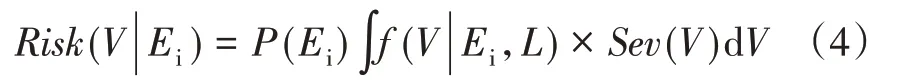
式（4）中，低電壓嚴重度取決于事故后節點的電壓，嚴重度函數如式（5）所示，曲線如圖2所示。

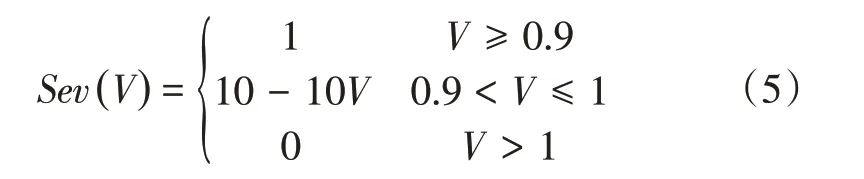
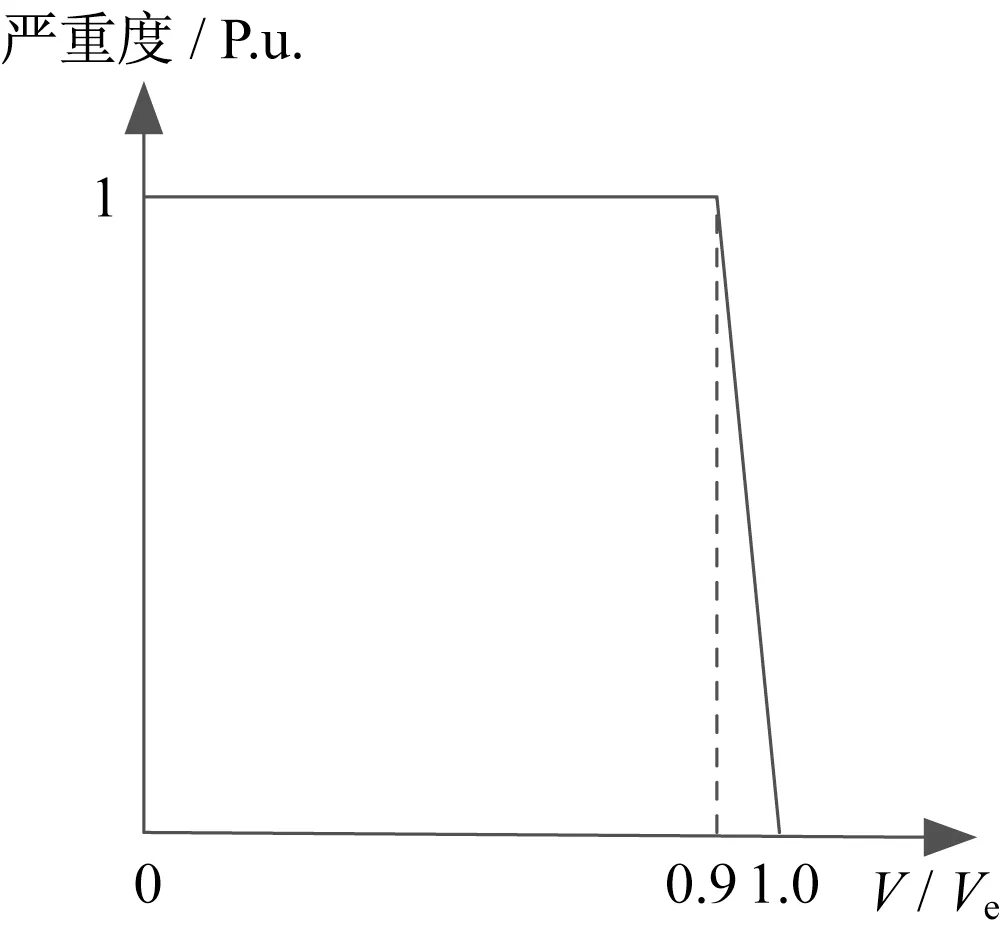
圖2 低電壓嚴重度函數Fig.2 Severity function of low voltage risk

3）失負荷風險

失負荷風險是事故后系統負荷節點失去負荷的可能性和嚴重程度的結合，即：

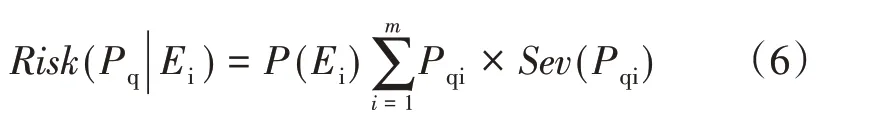
式（6）中，m為負荷節點數，Pqi為事故Ei后第i個負荷節點失去的負荷。

其中，失負荷嚴重度取決于失去負荷的比例，其嚴重度函數如式（7）所示，曲線如圖3所示。

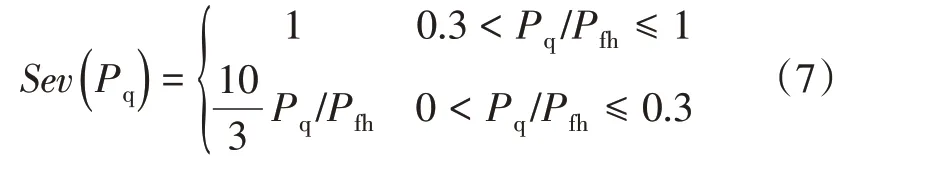
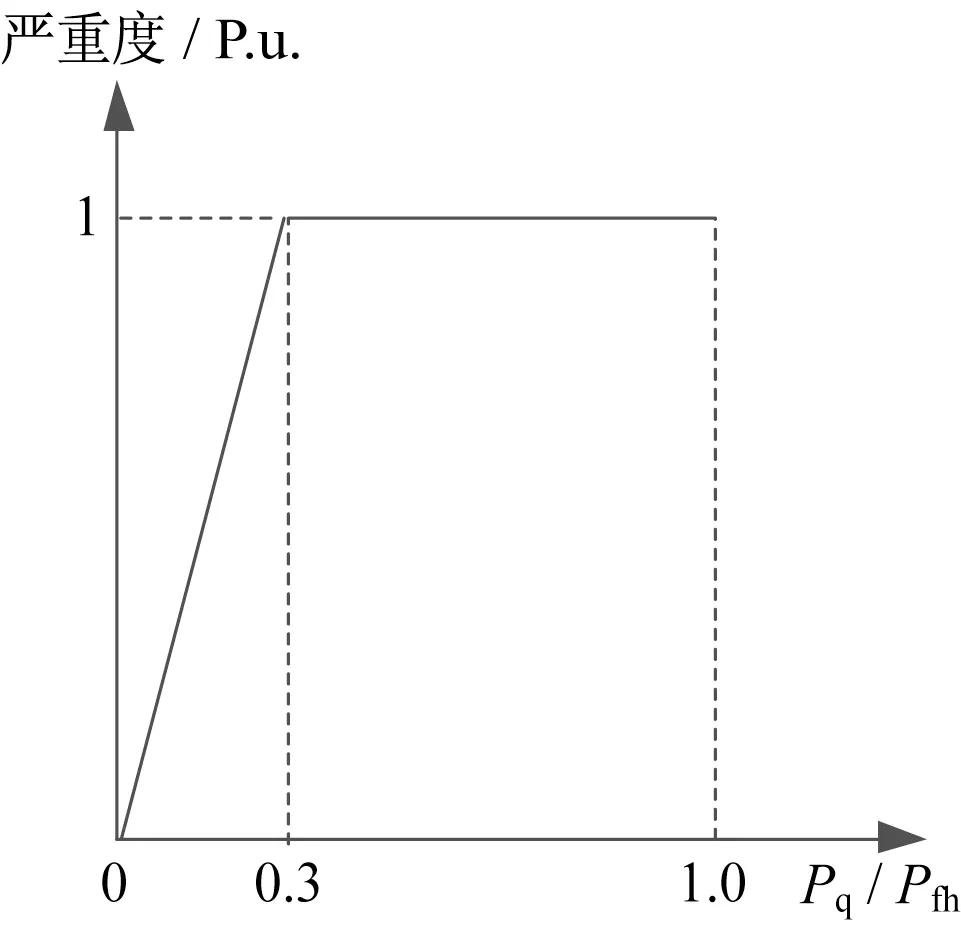
圖3失負荷嚴重度函數Fig.3 Severity function of lostload risk

1.2 基于ISODATA聚類的支路重要性分級

ISODATA聚類，即迭代自組織數據分析算法［26-28］，是一種非監督動態聚類算法的模式識別方法。ISODATA采用歐氏距離來分析數據本身的相似度，其核心思想是歐氏距離越小，相似度越大，將相似度高的數據自動聚集在一起。其基本步驟如下：

1）設置參數：待分類樣本xi；預期的聚類中心數目K；初始的聚類中心數目Nc；每一聚類域中最少的樣本數目θN；聚類域中樣本距離分布的標準差θS；兩聚類中心之間的最小距離θC；判斷循環停止的迭代運算的次數IP；兩聚類中心之間的距離Dij。

2）隨機選取Nc個樣本作為初始聚類的中心；

3）將樣本xi分配到最近的聚類Sj。規則為：若Dj=min(‖ ‖xi-Cj)，i=1，2，…，p，j=1，2，…，c，則將xi歸到聚類Sj。

4）計算各聚類的中心：

將新的中心值定為聚類的中心Ci=Zi。

5）分裂。若當前聚類的數目少于預期的聚類數目K，則開始進行聚類分裂。

6）合并。當兩個聚類的中心距離小于二者中心的最小距離θC時，兩個聚類合并為一個新的聚類。若全部聚類中心之間的距離Dˉij=‖ ‖Ci-Cj＜θC，就開始合并。新聚類中心為：

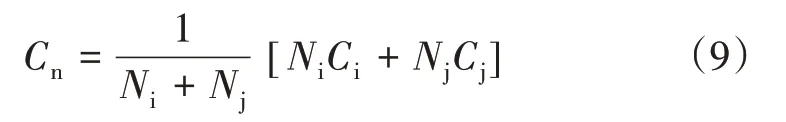
7）如果迭代次數達到最大迭代次數IP，或過程收斂，則迭代過程結束，否則IP=IP+1，回到步驟3。

支路重要性分級的思想即設定事故集為單一支路退運，分別計算出該退運線路的過負荷風險、低電壓風險和失負荷風險，將每條支路的三個風險值表示成一個三維風險向量，采用ISODATA算法將三維風險向量按照數據相似度聚類，得到每一級的聚類中心和支路編號，實現每條支路重要性等級初步自動分級。

2 基于PCA的支路重要性排序及分級調整

2.1 主成分分析PCA

主成分分析（PCA）方法［29-32］是一種廣泛應用于模式識別領域尋找多維數據主要特性的統計分析方法，其主要目的是將高維數據投影到低維空間，從多維數據中解析出主要成分，揭示多維數據有效信息，簡化分析復雜問題。

PCA的主要思想是對原N維列向量使用線性變換，得到按照重要性由高到低排序的新的N列向量。在得到的新列向量中選取重要性最大的M（M＜N）維子向量，作為原列向量的主成分。

記x1，…，xp為原始列向量的p個分量，設變換后列項的分量ξi，i=1，2，…，p，是原列向量子分量的線性組合，設定線性組合系數的模為1，即

這p個αi構成特征變換矩陣A。最優的正交變換A的每個分量αi使對應ξi的方差達到極值，數據將更加離散可分，相似性更低，也就代表了更多的信息。同時要求組成A的每個列向量兩兩正交，保證得到的新分量間兩兩不相關。此外，如果某維分量的方差越大，該分量就越重要，擁有更多的信息。

2.2 基于PCA的支路重要性排序及分級調整

以三維風險向量作為源數據，利用PCA方法對三維風險向量進行降維，保留源數據中的主要信息，得到所有三維風險數據的最大主方向，然后將三維風險向量投影到主方向軸線上就可以獲取能夠清晰分辨不同類別（即ISODATA自動分類結果）的一維數據，進而參照PCA降維結果來進行綜合風險指標計算。第一主成分ξ1即為綜合風險，計算公式如式（11）所示。

根據式（11）得到所有支路的綜合風險，根據綜合風險值進行支路重要性排序，綜合風險越大，該支路故障后對整個電力系統的影響越大，因此該支路越重要。

根據支路重要性排序結果，標注空間分級投影的上下邊界支路，如果相鄰兩重要級別支路的投影不存在交叉，則可以設定這兩級的分級點為該兩級的邊界支路的風險平均值；如果存在允許范圍內的交叉，則以重要等級高的邊界支路風險為準，落在邊界支路遠離原點方向的投影點均自動設定為偏重要等級，按照新的兩級邊界支路的風險平均值作為這兩級的分級點。設定分級交叉百分比為交叉支路數Njc占所有支路數Nz的百分比，如式（12）所示。

當分級交叉百分比滿足ψ＜10%時，可認為，采用第一主成分能夠綜合體現p個指標的三維空間分級信息，即分級交叉在允許范圍內。

3 基于模式識別的支路重要性評估

采用ISODATA聚類算法和PCA方法，完成了支路重要性評估，流程見圖4。

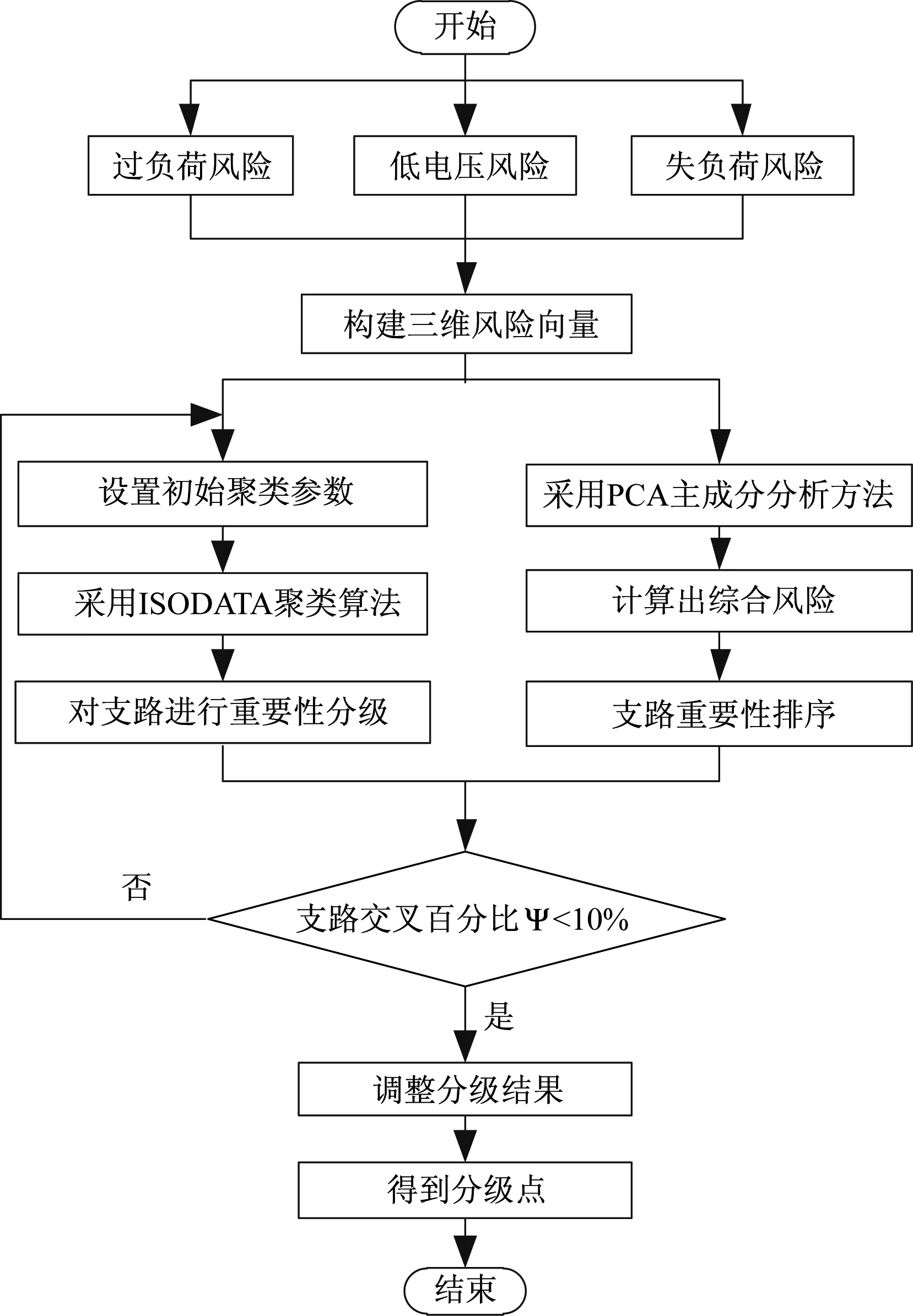
圖4 基于模式識別的支路重要性評估流程圖Fig.4 Assessment flowchart of branch importance based on pattern recognition

基于模式識別的電力系統支路重要性評估的具體流程分為四步：

第一步，計算所有支路的三種風險指標。設定故障為單一支路退運，分別計算出該退運支路的過負荷風險、低電壓風險和失負荷風險，將該支路的3個風險值表示成一個三維風險向量。同理，可以得到系統中其他所有支路的三維風險向量。

第二步，采用ISODATA算法對支路重要性進行分級。采用迭代自組織數據分析算法將所有支路的三維風險向量按照數據相似度聚類，實現支路退運風險等級初步自分級。以聚類中心與原點歐式距離的大小來判斷支路重要性等級。聚類中心距離原點越遠，該級別所包含的三維風險點距離原點越遠，因此這些風險點的風險就越大，其所屬重要性級別就越重要。

第三步，采用PCA方法對支路重要性進行排序。采用主成分分析方法對三維風險向量進行分析，得到能夠清晰分辨不同重要性級別的第一主成分，以此作為綜合風險指標綜合風險指標，從而完成支路重要性排序。

第四步，調整分級結果，得到分級點。將支路重要性分級與排序的結果進行比較分析，得到交叉支路，根據交叉支路百分比來判斷ISODATA聚類的可行性和科學性。若滿足判據，則對分級結果進行調整，找出新的分級邊界支路，確定每一級的分級點；若判據不滿足，則重新設定聚類參數進行支路重要性分級。

4 算例分析

4.1 算例設置

以IEEE39節點系統為例，設定負荷分配因數的波動為5%，并以此作為系統運行參數的變化。設預想事故集為系統中的每一條支路依次斷開，這些支路的年開斷率λy均是0.3。

根據骨干網架搜索的需要，設定支路重要性級別為三個等級，一級最為重要，二級其次，三級重要性級別最低。ISODATA算法的初始聚類中心為系統中任意三條支路的三維風險點。

4.2 支路重要性分級

經過仿真計算，得到過負荷嚴重度，低電壓嚴重度和切負荷嚴重度，對應的風險值即為所算得的嚴重度與故障發生概率的乘積，三維風險向量如圖5所示。采用ISODATA算法，對46條支路的三維風險進行重要性分級，分為一級、二級和三級，分別用*、+和·表示，每一類的聚類中心見表1和圖5所示。

從表1可以看出，一級支路聚類中心的三個風險值均大于二級支路的聚類中心風險值，同理，二級支路的大于三級支路的聚類中心風險值。因此，重要性級別越高，其聚類中心的三個風險值比低級別的聚類中心風險值越大，該級別的所有支路相對于低級別的支路就越重要。

表1 基于ISODATA算法的支路重要性分級結果Table 1 Classification result of branch importance based on ISODATA algorithm

4.3 支路重要性排序及分級調整

采用PCA方法分析支路退運的三維風險向量，得到所有三維風險向量的第一主成分，將所有三維空間風險點向對應于第一主成分的主方向軸作投影，如圖5所示，得到三維風險歸一化的權重系數向量為：

圖5 基于風險及模式識別的支路重要性分級圖Fig.5 Grade chart of branch importance based on risk and pattern recognition

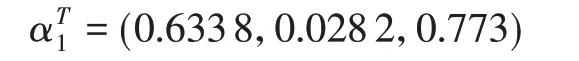
根據αT1和所有支路的三維風險向量，再結合式（11），可以計算出所有支路風險降維后的綜合風險值。選取不同重要性級別的邊界支路風險值列于表2所示。

對綜合風險進行降序排列，得到支路重要性排序圖，如圖6所示。

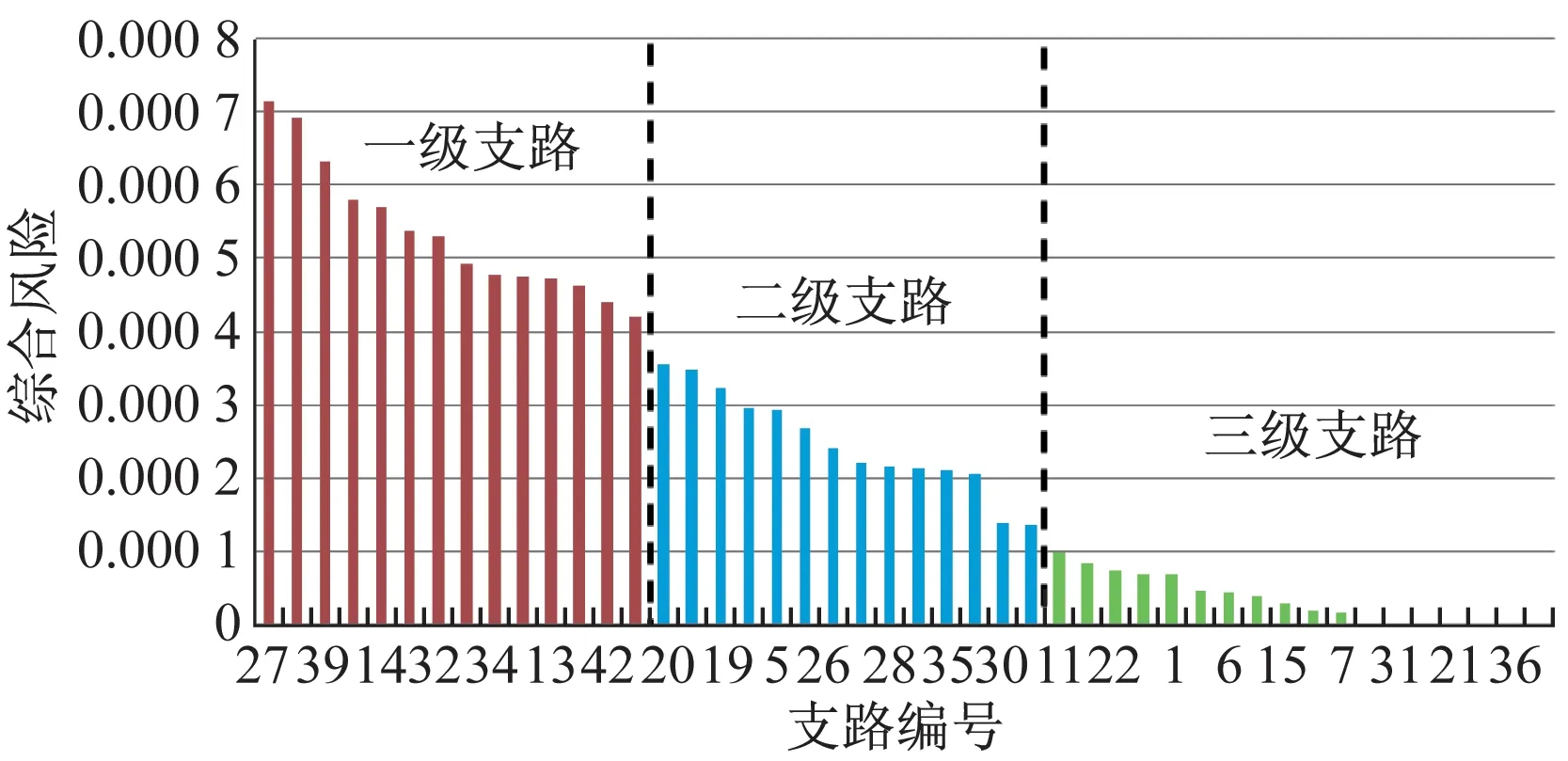
圖6 基于PCA方法的支路重要性排序及分級調整圖Fig.6 Rank and grade adjustment chart of branch importance based on PCA method

結合圖5和圖6可以看出，一級與二級的邊界支路風險落差大，兩級別不存在交叉支路，因此分級點為3.877×10-4。而二級與三級的邊界風險落差小一些，且存在交叉，分級交叉支路為L30（在表1中加粗標紅）。這是因為ISODATA聚類將相似三維風險向量聚為一類，雖然L8和L30的綜合風險很接近，但由于二級的聚類中心和L8的三維風險點均偏向軸Y（低電壓風險）的正方向，根據聚類的相似性特點可知，L8為二級支路是合理的。由于Nz=1，ψ=2.2%＜10%，在允許范圍內。以二級分界支路為準，L8為二級支路的下分界，L11為三級支路的上分界，因此該兩級別的重要性分級點為1.178×10-4，分級點如表2所示。

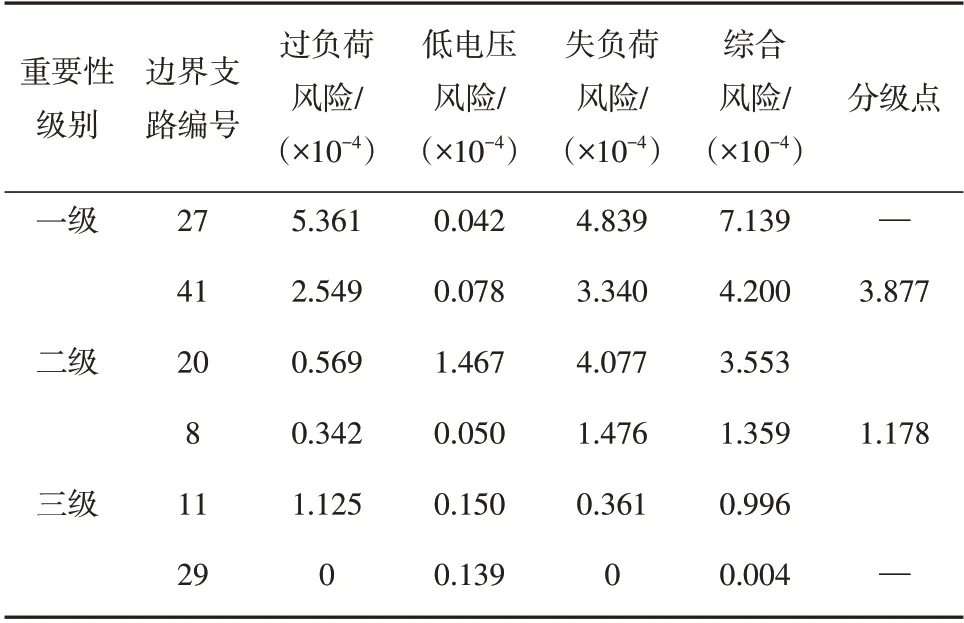
表2 邊界支路風險及分級點Table 2 Risk of boundary branches and Classification point

表2選取了支路分級的上邊界和下邊界支路進行羅列，各級別的綜合風險是依次降低的，各分指標總體上是降順排列的，但也存在特例，例如三級支路11的過負荷風險1.125大于二級支路8的過負荷風險0.342。由于L8比L11的失負荷風險大很多，因此L8比L11的綜合風險大，L8更重要是合理的。

采用聚類算法進行空間分類，以風險點距離最短為分類條件進行的風險指標值的分類，減少了人為因素的影響，更具有普適性，趨于智能分類結果。

5 結論

本文提出了電力系統支路重要性評估的新方法，采用ISODATA聚類算法，根據支路退運風險指標的相似性進行三維風險向量的初步自組織分級；采用PCA方法對電力系統的三維風險向量進行了降維分析，以所有風險向量第一主成分作為綜合風險值，對所有支路的綜合風險值進行排序，實現了電力系統支路重要性分級和排序。

以IEEE39節點系統為例進行仿真計算，仿真結果表明初步分級與重要性排序結果存在的交叉支路百分比ψ＜10%在允許范圍內，驗證了這種風險分級和綜合方法的有效性和可行性。該方法也適用于IEEE118節點系統，以及實際電網系統的支路重要性分級與排序。將ISODATA聚類算法與主成分分析方法相結合在電力系統支路重要性評估中的應用，為綜合指標的計算以及重要性支路的選取提供了一種有效且智能的方法，從而為構建核心骨干網架提供了理論支撐。