基于小樣本失效數據的復雜裝備可靠性評估研究進展與挑戰

李志強 汪新 陳宇奇 顧鈞元

摘 要： 隨著集機、電、液等技術于一體的復雜系統朝著高可靠性、長壽命、高成本等方向發展，在可靠性定時截尾試驗中經常出現小樣本失效數據，甚至無失效數據情況。在闡述整機級、系統級復雜裝備具有可靠性數據多源、數據信息不確定、連續性執行任務等特點的基礎上，分別從先驗信息、數據擴充和多源信息融合3個方面綜述了小樣本失效數據可靠性評估的研究現狀，概括分析現有研究存在的不足，展望了今后復雜裝備可靠性評估的發展趨勢和研究重點，提出了應用貝葉斯網絡表征復雜裝備不確定性量化過程的新思路，開展了基于可靠性評估的集群裝備選擇性維修優化研究。

關鍵詞：小樣本;可靠性評估;不確定性;貝葉斯網絡;選擇性維修

中圖分類號： TJ760.6+23; TB114.3? 文獻標識碼： A 文章編號：1673-5048（2021）03-0083-08

0 引? 言

高端武器裝備的可靠性水平是衡量綜合國力、凸顯國際競爭力的關鍵因素，因此，《中國制造2025》強調大力提高國防裝備質量、可靠性和壽命，增強國防裝備的實戰能力。

由于集機、電、液等技術于一體的航天飛機、大型艦船、運載火箭等復雜系統具有高可靠性、長壽命、高成本等特點，在可靠性定時截尾試驗中經常出現小樣本失效數據，甚至無失效數據情況，以致基于大數定理的經典可靠性評估方法難以適用[1-4]。雖然在復雜裝備的研制過程中進行了各種可靠性試驗以確保系統的可靠性水平，但是，大型武器裝備具有典型的訂單式生產特點，即品種少、數量少，研制階段可用于試航、試飛等試驗任務的裝備總量屈指可數。

根據試驗目的的不同，可靠性試驗可以分為環境應力篩選試驗、可靠性增長試驗、可靠性鑒定試驗、可靠性驗收試驗和可靠性測定試驗。對于成敗型復雜系統而言，大部分可靠性試驗具有一定的破壞性，因而無法開展大量試驗。此外，“經濟可承受性”的提出也要求在裝備的研制過程中充分考慮人力、物力、財力、安全性等因素。

因此，開展小樣本失效數據條件下的復雜裝備可靠性評估研究具有極為迫切的工程實踐需要，已逐漸成為近年來國內外的研究熱點。通過課題研究可以準確確定復雜系統的可靠性指標，改進設計和制造工藝，縮短裝備的研制周期，把握裝備性能退化規律，及時制定科學可行的維修決策，從而節約裝備運行和維護成本，推動傳統的定期維修模式向視情維修模式轉變。

1 小樣本失效數據裝備可靠性評估難點

小樣本失效數據指裝備在可靠性定時截尾試驗中只有少量失效事件發生或者沒有失效事件發生，數據信息樣本量小，以致無法采用基于概率理論的經典可靠性分析方法進行可靠性評估。由于整機級、系統級復雜裝備具有如下特點，目前難以利用單一來源的數據信息直接確定系統的可靠性指標，現以慣性導航系統為代表進行簡要分析：

（1） 慣性導航系統在研制、設計、生產、試驗、使用等各個階段，除了故障失效數據，還有加速壽命試驗數據、仿真數據、性能退化數據、狀態監測數據、專家經驗以及相似裝備歷史數據等信息，呈現出多源、多階段、多格式的特點。如果單一地使用某種數據信息，不僅造成其他數據資源的浪費，還會使得可靠性評估結果不夠客觀、準確，影響后續維修決策的制定。

（2） 慣性導航系統在技術選擇、冗余設計、參數擬定、材料篩選、方案規劃等各個環節都涉及到不確定信息，即不精確、不完整、甚至完全未知的信息，以致出現元件壽命分布模型不確定、模型參數不確定等情況。因此，在進行可靠性評估分析時還需要特別考慮不確定信息對裝備可靠性評估的影響，以確保評估結果的準確性和可信性。

（3） 隨著慣性導航系統功能日益強大、結構日趨復雜，出現故障的可能性越大，因而造成的風險和損失也就越大。此外，慣性導航系統的運行成本和綜合保障費用逐漸增長，“經濟可承受性”成為了一個新問題。傳統的“多維修、多保養”方式不僅導致了高額保障成本，也無法從根本上確保慣性導航系統的運行可靠性，反而影響了裝備連續性地執行任務。

可見，以慣性導航系統為代表的整機級、系統級復雜裝備具有可靠性數據多源、數據信息不確定、連續性執行任務等特點，使得基于小樣本失效數據的復雜裝備可靠性評估以及后續的維修決策優化成為了理論研究與工程實踐上的難題。

2 小樣本失效數據裝備可靠性評估方法

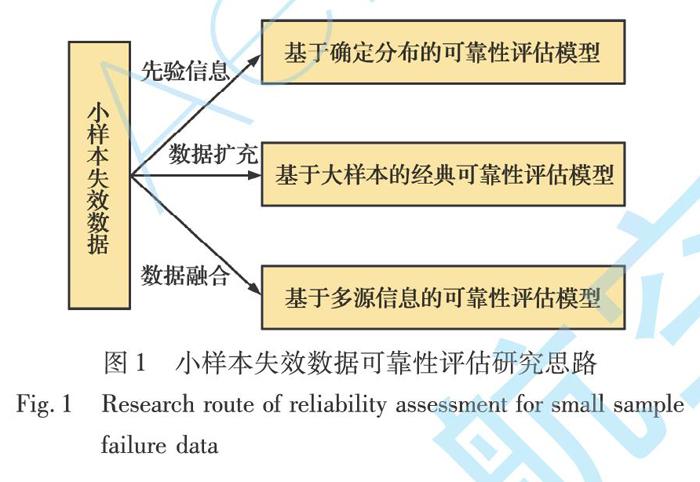
小樣本失效數據復雜裝備可靠性建模主要有三個思路[5-8]：（1）根據先驗信息建立可靠性評估模型;（2）擴充數據樣本，將小樣本問題轉化為大樣本問題處理;（3）融合退化數據、壽命數據和專家經驗等多源數據信息進行綜合分析，如圖1所示。

2.1 基于先驗信息的可靠性評估方法

基于先驗信息的可靠性評估方法一般根據專家信息進行模型構建[9-12]，即通過專家經驗給定裝備可靠性分析使用模型，如指數分布模型、正態分布模型、威布爾分布模型等，以可靠性預計數據或相似裝備故障數據作為先驗信息確定模型參數，進而根據元件故障失效數據或者性能退化數據確定裝備可靠度函數。文獻[13]應用最優置信限法、最小二乘估計確定了壽命服從指數型分布的MEMS傳感器在無失效數據條件下的可靠性指標;文獻[14]對壽命服從指數分布的串并聯系統進行了單元試驗時間、故障數向系統層級上的折算;文獻[15]將失效信息引入置信限分析中，通過參數估計與時間系數等效替換等方法確定了無失效數據機電產品的可靠度和平均故障間隔時間;文獻[16]提出了一種基于蒙特卡洛方差減少技術失效事件概率的快速計算方法，評估電力傳輸網絡中級聯失效稀有事件的發生概率，降低了傳統蒙特卡洛方法的仿真計算量與運行時間;針對多狀態節點條件概率值難以確定的問題，文獻[17-18]應用DS證據理論融合處理多個專家信息，確定了貝葉斯網絡中間節點的信任函數、似然函數，避免了單個專家推斷存在的片面性，同時降低了主觀因素引起的認知不確定度。

基于先驗信息的可靠性評估方法以長期積累的數據信息、專家經驗為前提，構建確定分布條件下的可靠性分析模型。該方法適用于改進型元器件，但對于缺乏數據信息和專家經驗的新研制元器件不適用。

2.2 基于數據擴充的可靠性評估方法

基于數據擴充的可靠性評估方法適用于小樣本失效數據裝備，無法應用于無失效數據裝備。對于壽命分布無先驗信息的產品，文獻[19]應用GM預測模型進行試驗樣本擴容，進而應用Bootstrap方法進行未知參數估計，該方法適用于威布爾分布模型、Gamma分布模型等;文獻[20]應用改進的Bootstrap方法對電氣設備小樣本數據進行擴容，進而根據形態相似距離進行曲線擬合，實現對電氣設備可靠性指標的預測估計;文獻[21-22]采用虛擬增廣原理擴充試驗數據，借助極大似然法估計樣本參數，進而應用Wiener過程描述了正態分布模型的可靠性指標退化過程;文獻[23]通過擬合壽命概率分布曲線確定了產品的可靠度點估計，又通過Bootstrap方法擴容確定了產品的可靠度置信區間;文獻[5]應用隨機過程構建了復雜系統性能退化模型，確定了系統性能分布、失效時間分布、可靠度等指標的表達式，該方法適用于無失效數據產品以及樣本數小于5的小樣本產品。

基于數據擴充的可靠性分析方法適用于有一定樣本量失效數據或性能退化數據的元器件。但是，對于失效數據極少的元器件，如單失效數據元器件，無法進行數據擴容。此外，對于缺乏數據信息的元器件，該方法也不適用。

2.3 融合多源數據信息的可靠性評估方法

對于復雜裝備可靠性評估而言，小樣本失效數據有兩種情況：（1）由于設計改良、新技術應用等因素，系統中只存在單個元件小樣本失效數據情況;（2）復雜系統中某個子系統或多個元件為新引入模塊，出現多個元件為小樣本失效數據情況。

2.3.1 單個元件小樣本失效數據裝備

只引入了單個新元件的復雜系統比較常見，其可靠性分析思路為：通過融合多源數據信息，確定新元件在小樣本失效數據條件下的可靠性指標，進而根據復雜系統的模型結構、失效模式、故障機理確定系統的可靠性參數。文獻[24]提出了一種基于動態故障樹的稀有事件仿真方法，該方法降低了傳統故障樹分析中蒙特卡洛方法的仿真量;文獻[25]應用經驗Bayesian方法構建了失效數據稀缺產品的可靠性評估模型，進而確定了點估計值和區間估計范圍;文獻[26]應用相關函數融合樣本數據和驗前數據確定了復雜系統中底事件的可靠度，在此基礎上，構建T-S模糊故障樹對多狀態系統進行了可靠性評估。

2.3.2 多個元件小樣本失效數據裝備

包含單個新元件的復雜系統可靠性試驗以新元件單獨試驗為主，較少以系統或者子系統的形式開展試驗。然而，包含多個新元件的復雜系統除了單個元件的可靠性試驗，還包括系統級或者子系統級的試驗。相對而言，包含多個新元件的復雜系統失效模式更加多樣、故障機理更加復雜，其可靠性分析更具有挑戰性。為了利用元件試驗數據彌補系統試驗數據的不足，文獻[14]引入定時截尾試驗方案下失效率的近似概率密度函數，將元件試驗的故障數據和試驗時間折合為系統試驗的等效故障數據和試驗時間;文獻[27]應用基于PHM技術的狀態監測系統，采集有線通信系統的性能狀態指標，根據系統可靠性分析結果提前制定優化的維修決策，從而避免不必要的停機;文獻[28]在文獻[29-31]中E-Bayesian估計理論基礎上，提出了一種不依賴于先驗信息的串聯、并聯系統可靠性指標確定方法;文獻[32-33]通過引入老化因子構建了處于退化階段的復雜系統性能衰退可靠性評估模型，描述了系統及元件性能指標隨時間的變化趨勢，并根據分析結果制定了相應的維修決策。

融合多源數據信息的可靠性分析方法綜合利用了元件在不同階段、不同運行環境積累的數據信息，可確保可靠性分析結果的客觀性、準確性。該方法的關鍵在于如何選取合適的方法從多源數據中篩選出合適的數據信息，既不浪費數據資源，又不影響評估結果的科學性、全面性。

3 發展趨勢與未來展望

由于以慣性導航系統為代表的整機級、系統級復雜裝備具有可靠性數據多源、數據信息不確定、連續性執行任務等特點，現有研究還存在以下不足：

（1） 現有的小樣本失效數據復雜裝備可靠性評估方法一般預先假設部件壽命服從某一分布，或者人為給出分布模型參數，忽略了不確定性的影響。在綜合利用退化數據、壽命數據、專家經驗、狀態監測數據等多源數據信息進行可靠性建模和評估時，缺少了不確定性量化過程。

（2） 在復雜裝備可靠性評估過程中，一般以區間函數方式分析部件的可靠性參數不確定性，忽略了不確定性在復雜系統中的傳播問題。此外，現有研究主要針對新裝備或者服役裝備在某一時刻的不確定性問題，缺少引入時間變量的動態可靠性分析過程。

（3） 當前，復雜裝備的選擇性維修主要針對串并聯系統，無法應用于橋式結構、網絡結構，而現有復雜裝備已不再只是簡單的串并聯結構。此外，相對于單裝備工作模式，越來越多的裝備以集群的方式開展工作，因此，集群裝備的選擇性維修已成為了一個突出問題。

上述三個方面的問題揭示了小樣本失效數據復雜裝備可靠性評估面臨的挑戰以及未來可能的發展趨勢。

3.1 引入不確定性的復雜裝備可靠性評估

在復雜裝備的研制、設計、生產、試驗、使用等各個階段，技術選擇、冗余設計、參數擬定、材料篩選、方案規劃等各個環節都涉及到不確定信息，即不精確、不完整、甚至完全未知的信息，具體包括：數據缺乏導致的不確定信息、不完全知識經驗導致的不確定信息、不同識別模式導致的不確定信息等[34-38]。從信息來源看，不確定性可以分為隨機不確定性和認知不確定性：前者來源于系統固有偶然性或變異性，無法避免;后者由知識的不完備性以及數據缺乏造成，受數據信息、知識經驗、試驗條件等影響[39-41]。

在傳統的可靠性分析研究中，通常應用概率理論和模糊集理論處理不確定問題，然而，在工程實踐中由于環境、技術、成本、時間等原因缺乏大量統計觀測數據，因此，傳統方法選用模型的參數概率分布和隸屬度函數難以確定，出現元件壽命分布模型不確定、模型參數不確定，進而影響了可靠性評估結果的準確性和科學性[42-43]。由于隨機不確定性無法避免，當前的不確定性研究主要針對認知不確定性展開。鑒于不確定信息難以用精確語言描述，國內外學者應用專家經驗量化、確信可靠性理論、區間集合理論、DS證據理論、貝葉斯網絡等方法對復雜裝備可靠性分析中涉及的不確定性開展研究[44-47]。作為可靠性分析領域的新方法，確信可靠性理論引入不確定測度描述系統的認知不確定性，應用概率論描述隨機不確定性，應用機會理論描述混合不確定性。

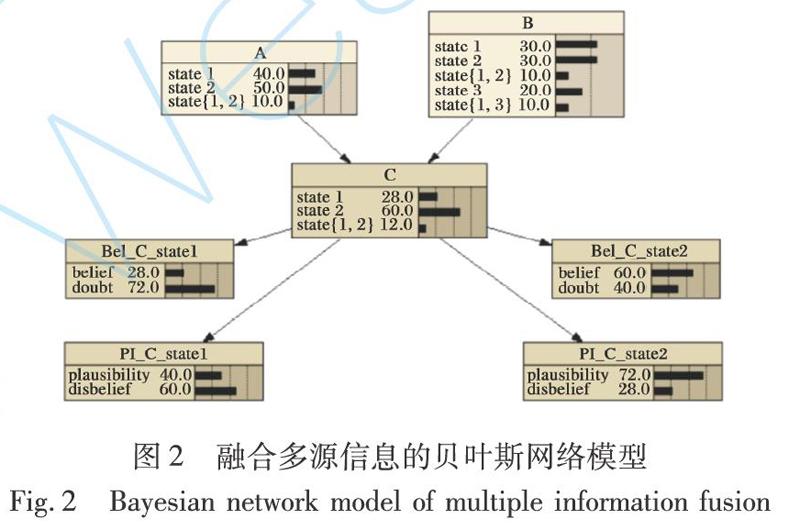
以貝葉斯網絡方法為例表達不確定性，如圖2所示，二狀態裝備C由二狀態元件A和三狀態元件B構成。由于不確定性的存在，貝葉斯網絡中節點A由兩個狀態拓展為三個狀態，包括一個不確定度狀態，節點B由三個狀態拓展為五個狀態，包括兩個不確定度狀態。由節點C延伸出兩個置信節點和兩個似然節點，分別表示節點處于狀態1和狀態2的置信度和似然度。應用MC仿真方法可以驗證所建模型的準確性。

3.2 基于貝葉斯網絡的復雜裝備可靠性評估

Bayesian方法在融合處理多源、多階段失效數據方面具有巨大優勢，已廣泛應用于裝備可靠性參數的確定中。然而，復雜裝備可靠性評估主要針對單元件裝備或結構簡單的串并聯系統，對于結構復雜的多元件裝備，Bayesian方法涉及復雜的多重積分，難以適用。鑒于貝葉斯網絡在復雜系統可靠性建模中的巨大優勢[48-55]，課題組擬采用Bayesian方法處理具有多源數據信息的元件，在此基礎上，應用貝葉斯網絡進行復雜裝備可靠性建模與分析，研究思路如圖3所示。對于具有失效數據、相似裝備數據、加速壽命試驗數據等多源數據信息的部件，在統計量相容性檢驗的基礎上，應用Bayesian方法進行數據融合，確定貝葉斯網絡根節點的可靠性指標;對于無數據信息的部分新研部件，充分利用專家經驗信息確定根節點可靠性指標置信范圍。貝葉斯網絡中間節點條件概率值通過布爾邏輯關系確定，對于難以確定的多狀態中間節點擬應用DS/AHP方法融合專家經驗信息確定[17]。

作為多源數據融合的基礎，t檢驗可以判斷多源數據是否服從同一分布，以可靠度總體服從正態分布的機電裝備零部件為例，t檢驗統計量表示為

t=X-μσxn-1（1）

式中：t為樣本與總體分布的離差統計量;X為樣本平均值;μ為總體平均數;σx為樣本標準差;n為樣本容量。

當設定α為顯著水平時，比較樣本離差t與臨界值t（n-1）a之間的大小關系。若t

根據復雜裝備的結構組成構建貝葉斯網絡模型，應用Bayesian方法、DS理論確定根節點處于各狀態的概率，借助DS/AHP方法確定多狀態中間節點條件概率值，進而利用貝葉斯網絡的前向推理確定裝備可靠性指標，清晰表達不確定性在模型中的傳播過程以及量化各個不確定性要素對系統性能指標的影響，量化過程如圖4所示。進而根據不同的不確定性來源合理分配資源，降低系統不確定性和管理風險。然而，在不確定性量化過程中面臨著如下主要挑戰：（1）復雜裝備元件多、數據多、結構多樣，如何進行模型不確定性降維;（2）個別輸入變量既包含隨機不確定性又包含認知不確定性，如何將二者有效分離，進而采取相應措施降低認知不確定性對輸出變量產生的影響;（3）如何在動態貝葉斯網絡中表征非線性變量、靜態節點以及非根節點與上一時間片中非根節點之間存在的依賴關系;（4）如何在貝葉斯網絡中表征共因失效、競爭失效。

3.3 基于可靠性評估的選擇性維修優化

選擇性維修指在任務間隔期對連續執行多個任務的復雜裝備中的老化或者失效部件進行維修，以確保后續任務的順利完成[56-60]，如圖5所示。選擇性維修受維修成本、維修時長、備件庫存、維修人員數量等因素的制約，在任務間隔期內選擇性地對部分裝備部件采取維修措施，從而最大程度地確保后續任務的完成。相比于事后維修、定期維修，選擇性維修屬于有限資源約束條件下的視情維修，具有如下特點：（1）部件維修選擇性，不一定是所有老化或者失效部件，不同的選擇性維修方案消耗不同的資源，獲得不同的維修效果;（2）維修時間限制性，只能在任務間隔期對裝備采取維修措施;（3）面向任務成功性，不同于以往的優化維修模型，選擇性維修追求有限資源約束條件下系統的最大任務成功概率;（4）維修決策動態性，由于復雜裝備系統及部件性能狀態隨時間變化，任務具有隨機性、模糊性，單裝備、集群裝備的選擇性維修策略需要動態調整。

與復雜裝備可靠性評估類似，選擇性維修現有研究主要圍繞串并聯系統的模型構建、維修程度選擇、維修資源優化、任務特性分析、智能優化算法五個方面展開，各方面又相互交叉[61-65]。隨著研究深入，選擇性維修也逐漸拓展到了集群裝備領域，如文獻[66]以費用為約束條件，構建了集群裝備任務成功概率最大化的選擇性維修優化模型，為降低計算量將非線性目標函數線性化近似處理;文獻[67]以階段性任務必須滿足的可靠度指標為約束條件，以所有關鍵子系統的有效剩余壽命為輸入變量，構建了集群裝備選擇性維修優化模型;文獻[68]在分析裝備結構、任務性質、競爭失效等因素模糊特性的基礎上，構建了集群裝備在競爭失效條件下的模糊多狀態系統選擇性維修模型。但是，隨著不確定性引入復雜裝備可靠性評估分析中，選擇性維修建模還需在如下方面進行完善：（1）如何構建橋式結構復雜系統選擇性維修優化模型;（2）如何構建網絡結構復雜系統選擇性維修優化模型;（3）如何構建不同裝備組成集群的選擇性維修優化模型;（4）如何在建模過程中引入共因失效和競爭失效。

4 結 束 語

融合多源數據信息的可靠性評估方法為小樣本失效數據復雜裝備，尤其是無失效數據復雜裝備的可靠性評估提供了思路和途徑，已逐漸在數控機床、風力發電場、航天飛機、大型艦船等領域得到應用。發展多源數據融合可靠性評估、不確定性量化、動態可靠性分析、選擇性維修優化等前沿理論，有助于解決小樣本失效數據的復雜裝備可靠性分析與維修決策優化這一工程難題，其研究成果能夠改進現有大型整機級、系統級復雜裝備的綜合保障模式，節約復雜裝備保障成本、時間和人力，為后續制定優化的維修決策提供理論指導。

參考文獻：

[1] 陳文華，賀青川，潘駿，等. 機械產品可靠性試驗技術研究現狀與展望[J]. 中國機械工程， 2020， 31（1）： 72-82.

Chen Wenhua， He Qingchuan， Pan Jun， et al. Reliability Test Technology of Mechanical Products-Overview and Prospect[J]. China Mechanical Engineering， 2020， 31（1）： 72-82. （in Chinese）

[2] Balesdent M， Morio J， Marzat J. Recommendations for the Tuning of Rare Event Probability Estimators[J]. Reliability Engineering & System Safety， 2015， 133： 68-78.

[3] Bourinet J M. Rare-Event Probability Estimation with Adaptive Su-pport Vector Regression Surrogates[J]. Reliability Engineering and System Safety， 2016， 150： 210-221.

[4] Yang J W， Wang J H， Huang Q， et al. Reliability Assessment for the Solenoid Valve of a High-Speed Train Braking System under Small Sample Size[J]. Chinese Journal of Mechanical Engineering， 2018， 31（3）： 189-199.

[5] Wu Q， Yang J Z， Wang J Y， et al. Reliability Analysis of Degradation with a New Independent Increment Process[J]. Journal of Mechanical Science and Technology， 2014， 28（10）： 3971-3976.

[6] Chen W H， Cui J， Fan X Y， et al. Reliability Analysis of DOOF for Weibull Distribution[J]. Journal of Zhejiang University：Science， 2003， 4（4）： 448-453.

[7] 陳文華，崔杰，樊曉燕，等. 單失效數據的可靠性統計分析[J]. 機械工程學報， 2003， 39（9）： 44-48.

Chen Wenhua， Cui Jie， Fan Xiaoyan， et al. Reliability Statistical Analysis of Data Only One Failure[J]. China Journal of Mechanical Engineering， 2003， 39（9）： 44-48. （in Chinese）

[8] 傅惠民，岳曉蕊，張勇波. 極少失效數據的可靠性評估和壽命預測[J]. 航空動力學報， 2010， 25（8）： 1855-1859.

Fu Huimin， Yue Xiaorui， Zhang Yongbo. Reliability Assessment and Life Prediction for Very Few Failure Data[J]. Journal of Aerospace Power， 2010， 25（8）： 1855-1859. （in Chinese）

[9] 王浩偉，滕克難，呂衛民. 導彈貯存延壽試驗關鍵技術及研究進展[J]. 含能材料， 2019， 27（12）： 1004-1016.

Wang Haowei， Teng Kenan， Lü Weimin. Review on Key Technologies for Missile Storage and Life-Extension Test[J]. Chinese Journal of Energetic Materials， 2019， 27（12）： 1004-1016. （in Chinese）

[10] 楊立健，趙敏，李強. 單臺件設備可靠性評估方法[J]. 水下無人系統學報， 2017， 25（3）： 288-292.

Yang Lijian， Zhao Min， Li Qiang. Reliability Evaluation Method for Single Equipment[J]. Journal of Unmanned Undersea Systems， 2017， 25（3）： 288-292. （in Chinese）

[11] 宋明順，魯偉，方興華. 基于小樣本失效數據的機械可靠性評估[J]. 工業工程， 2017， 20（5）： 87-93.

Song Mingshun， Lu Wei， Fang Xinghua. A Research on Mechanical Reliability Assessment Based on Small Sample Failure Data[J]. Industrial Engineering Journal， 2017， 20（5）： 87-93. （in Chinese）

[12] 郭銳，張榮兵，趙靜一，等. 單失效數據情形下蓄能器可靠性評估[J]. 中國機械工程， 2018， 29（16）： 1891-1899.

Guo Rui， Zhang Rongbing， Zhao Jingyi， et al. Reliability Evaluation of Accumulator in Single Failure Data[J]. China Mechanical Engineering， 2018， 29（16）： 1891-1899. （in Chinese）

[13] 佐磊，孫洪凱，何怡剛，等. 無失效數據的 MEMS 傳感器可靠性分析[J]. 電子測量與儀器學報， 2019， 33（6）： 69-75.

Zuo Lei， Sun Hongkai， He Yigang， et al. Reliability Analysis of MEMS Sensors with Zero-Failure Data[J]. Journal of Electronic Measurement and Instrumentation， 2019， 33（6）： 69-75. （in Chinese）

[14] 金俊坤，楊寧國，呂冬雪. 結合單元試驗數據的指數型串聯系統定時截尾試驗可靠性評估方法[J]. 兵工學報， 2019， 40（8）： 1756-1760.

Jin Junkun， Yang Ningguo， Lü Dongxue. Evaluation Method of Exponential Series System Reliability Based on Fixed Time Truncated Test and the Combination of System and Its Units Test Data[J]. Acta Armamentarii， 2019， 40（8）： 1756-1760. （in Chinese）

[15] 李海洋，謝里陽，李銘，等. 一種新的無失效數據可靠性評估方法研究[J]. 兵工學報， 2018， 39（8）： 1622-1631.

Li Haiyang， Xie Liyang， Li Ming， et al. Research on a New Reliability Assessment Method for Zero-Failure Data[J]. Acta Armamentarii， 2018， 39（8）： 1622-1631. （in Chinese）

[16] Cadini F， Agliardi G L， Zio E. Estimation of Rare Event Probabilities in Power Transmission Networks Subject to Cascading Failures[J]. Reliability Engineering & System Safety， 2017， 158： 9-20.

[17] 李志強，徐廷學，顧鈞元，等. 融合不確定信息的某型導彈控制系統可靠性分析方法[J]. 系統工程與電子技術， 2017， 39（12）： 2879-2886.

Li Zhiqiang， Xu Tingxue， Gu Junyuan， et al. Reliability Analysis of a Missile Control System by Fusing Uncertain Information[J]. Systems Engineering and Electronics， 2017， 39（12）： 2879-2886. （in Chinese）

[18] 徐廷學，李志強，顧鈞元，等. 基于多狀態貝葉斯網絡的導彈質量狀態評估[J]. 兵工學報， 2018， 39（2）： 391-398.

Xu Tingxue， Li Zhiqiang， Gu Junyuan， et al. Missile Condition Assessment Based on Multi-State Bayesian Network[J]. Acta Armamentarii， 2018， 39（2）： 391-398. （in Chinese）

[19] Xia X T. Reliability Analysis of Zero-Failure Data with Poor Information[J]. Quality and Reliability Engineering International， 2011， 28（8）： 981-990.

[20] 周凱，丁堅勇，田世明，等. 基于小樣本性能數據的電氣設備可靠性評估與預測方法研究[J]. 電網技術， 2018， 42（6）： 1967-1974.

Zhou Kai， Ding Jianyong， Tian Shiming， et al. Research on Assessment and Prediction of Electrical Equipment Reliability Based on Small Sample Performance Data[J]. Power System Technology， 2018， 42（6）： 1967-1974. （in Chinese）

[21] 張云，姜楠，王立平. 基于Wiener過程的數控轉臺極小子樣可靠性分析[J]. 清華大學學報： 自然科學版， 2019， 59（2）： 91-95.

Zhang Yun， Jiang Nan， Wang Liping. Reliability Analysis of NC Rotary Table Based on a Wiener Process for Extremely Small Samples[J]. Journal of Tsinghua University： Science and Technology， 2019， 59（2）： 91-95. （in Chinese）

[22] 張云，于廣，王立平，等. 基于性能退化數據的數控轉臺單子樣可靠性分析[J/OL]. 清華大學學報： 自然科學版， 2019. http：∥kns.cnki.net/kcms/detail/11.2223.N. 20191106. 20191540. 20191001. html.

Zhang Yun， Yu Guang， Wang Liping， et al. Performance Degradation Data Based NC Rotary Table Reliability Predictions Using a Single Sample[J/OL]. Journal of Tsinghua University： Science and Technology， 2019. http：∥kns.cnki.net/kcms/detail/11.2223.N.20191106. 20191540. 20191001. html. （in Chinese）

[23] Li H Y， Xie L Y， Li M， et al. Reliability Assessment of High-Quality and Long-Life Products Based on Zero-Failure Data[J]. Quality and Reliability Engineering International， 2018， 35（1）： 470-482.

[24] Ruijters E， Reijsbergen D， de Boer P-T， et al. Rare Event Simulation for Dynamic Fault Trees[J]. Reliability Engineering & System Safety， 2019， 186： 220-231.

[25] Quigley J， Bedford T， Walls L. Estimating Rate of Occurrence of Rare Events with Empirical Bayes： A Railway Application[J]. Reliability Engineering & System Safety， 2007， 92（5）： 619-627.

[26] 陸鳳儀，趙科淵，徐格寧，等. 基于多源信息融合及模糊故障樹的小子樣可靠性評估[J]. 工程設計學報， 2017， 24（6）： 609-617.

Lu Fengyi， Zhao Keyuan， Xu Gening， et al. Reliability Assessment of Small Sample Based on Multiple Source Information Fusion and Fuzzy Fault Tree[J]. Chinese Journal of Engineering Design， 2017， 24（6）： 609-617. （in Chinese）

[27] Lee J， Kown D， Kim N， et al. PHM-Based Wiring System Da-mage Estimation for Near Zero Downtime in Manufacturing Facilities[J]. Reliability Engineering & System Safety， 2019， 184： 213-218.

[28] Gholizadeh R， Londono S L M， Pereira M. Expectation Bayesian Estimation of System Reliability Based on Failures[J]. Methodo-logy and Computing Applied Probability， 2019， 21： 367-385.

[29] Han M. E-Bayesian Estimation of Failure Probability and Its Application[J]. Mathematical and Computer Modelling： An International Journal， 2007， 45（9/10）： 1272-1279.

[30] Han M. E-Bayesian Estimation and Hierarchical Bayesian Estimation of Failure Rate[J]. Applied Mathematical Modelling， 2009， 33（4）： 1915-1922.

[31] Han M. E-Bayesian Estimation of the Reliability Derived from Binomial Distribution[J]. Applied Mathematical Modelling， 2011， 35（5）： 2419-2424.

[32] Li Z Q， Xu T X， Gu J Y， et al. Performance Degradation Modeling for Multi-State Element Considering Aging Factor[J]. Mecha-nika， 2018， 24（2）： 260-267.

[33] 李志強，徐廷學，顧鈞元，等. 考慮老化因素的串聯系統不完全維修決策優化[J]. 控制與決策， 2019， 34（4）： 827-833.

Li Zhiqiang， Xu Tingxue， Gu Junyuan， et al. Optimal Maintenance Policies for Series Systems under Imperfect Repair Considering Aging Factor[J]. Control and Decision， 2019， 34（4）： 827-833. （in Chinese）

[34] 李志強，徐廷學，顧鈞元，等. 不確定條件下復雜系統可靠性建模與分析綜述[J]. 戰術導彈技術， 2018（6）： 13-19.

Li Zhiqiang， Xu Tingxue， Gu Junyuan， et al. Reliability Modeling and Analysis of Complex Systems under Uncertainty[J]. Tactical Missile Technology， 2018（6）： 13-19. （in Chinese）

[35] Nima K. System Safety Assessment under Epistemic Uncertainty： Using Imprecise Probabilities in Bayesian Network[J]. Safety Science， 2019， 116： 149-160.

[36] Hu L H， Kang R， Pan X， et al. Risk Assessment of Uncertain Random System-Level-1 and Level-2 Joint Propagation of Uncertainty and Probability in Fault Tree Analysis[J]. Reliability Engineering & System Safety， 2020， 198： 106874.

[37] Abrishami S， Khakzad N， Hosseini S M， et al. BN-SLIM： A Bayesian Network Methodology for Human Reliability Assessment Based on Success Likelihood Index Method （SLIM）[J]. Reliabi-lity Engineering & System Safety， 2020， 193： 106647.

[38] Kown Y C， Won J-H， Kim B J， et al. Uncertainty Quantification Using Bayesian Neural Networks in Classification： Application to Biomedical Image Segmentation[J]. Computational Statistics and Data Analysis， 2020， 142： 106816.

[39] Karanki D R， Rahman S， Dang V N， et al. Epistemic and Aleatory Uncertainties in Integrated Deterministic and Probabilistic Safety Assessment： Tradeoff between Accuracy and Accident Simulations[J]. Reliability Engineering & System Safety， 2017， 162： 91-102.

[40] Rahman S，? Karanki D R，? Epiney A， et al. Deterministic Sampling for Propagating Epistemic and Aleatory Uncertainty in Dynamic Event Tree Analysis[J]. Reliability Engineering & System Safety， 2018， 175： 62-78.

[41] Vincent C， Mathieu B， Jean-Marc B， et al. Reliability-Based Sensitivity Estimators of Rare Event Probability in the Presence of Distribution Parameter Uncertainty[J]. Reliability Engineering & System Safety， 2018， 178： 164-178.

[42] Zeng Z G， Kang R， Wen M L， et al. Uncertainty Theory as a Basis for Belief Reliability[J]. Information Sciences， 2018， 429： 26-36.

[43] Kabir S， Papadopoulos Y. Applications of Bayesian Networks and Petri Nets in Safety， Reliability， and Risk Assessments： A Review[J]. Safety Science， 2019， 115： 154-175.

[44] Lannoy A， Procaccia H. Expertise， Safety， Reliability， and Decision Making： Practical Industrial Experience[J]. Environment System and Decisions， 2014， 34（2）： 259-276.

[45] 彭文勝，張建國，張金洋，等. 混合不確定多態系統可靠性的EUGF分析方法[J]. 系統工程與電子技術， 2017， 39（12）： 2863-2868.

Peng Wensheng， Zhang Jianguo， Zhang Jinyang， et al. EUGF Analysis of Reliability of MSS Containing Hybrid Uncertainties[J]. Systems Engineering and Electronics， 2017， 39（12）： 2863-2868. （in Chinese）

[46] Li Z Q， Xu T X， Gu J Y， et al. Reliability Modeling of Redundant Systems Considering CCF Based on DBN[J]. Arabian Journal for Science and Engineering， 2019， 44（3）： 2567-2577.

[47] 于格，康銳，林焱輝，等. 基于確信可靠度的齒輪可靠性建模與分析[J]. 系統工程與電子技術， 2019， 41（10）： 2385-2391.

Yu Ge， Kang Rui， Lin Yanhui， et al. Reliability Modeling and Analysis of Gear Based on Belief Reliability[J]. Systems Engineering and Electronics， 2019， 41（10）： 2385-2391. （in Chinese）

[48] Mi J H， Li Y F， Yang Y J， et al. Reliability Assessment of Complex Electromechanical Systems under Epistemic Uncertainty[J]. Reliability Engineering & System Safety， 2016， 152： 1-15.

[49] 李志強，徐廷學，顧鈞元，等. 視情維修條件下的多狀態控制單元可用性建模與分析[J]. 兵工學報， 2017， 38（11）： 2240-2250.

Li Zhiqiang， Xu Tingxue， Gu Junyuan， et al. Availability Modeling and Analyzing of Multi-State Control Unit under Condition-Based Maintenance[J]. Acta Armamentarii， 2017， 38（11）： 2240-2250. （in Chinese）

[50] Mi J H， Li Y F， Peng W W， et al. Reliability Analysis of Complex Multi-State System with Common Cause Failure Based on Evidential Networks[J]. Reliability Engineering & System Safety， 2018， 174： 71-81.

[51] He R， Li X H， Chen G M， et al. A Quantitative Risk Analysis Model Considering Uncertain Information[J]. Process Safety and Environmental Protection， 2018（118）： 361-370.

[52] Li Z Q， Xu T X， Gu J Y， et al. Reliability Modelling and Analysis of a Multi-State Element Based on a Dynamic Bayesian Network[J]. Royal Society Open Science， 2018， 5（4）： 171438.

[53] 李志強，徐廷學，安進，等. 冗余系統共因失效動態貝葉斯網絡建模[J]. 儀器儀表學報， 2018， 39（3）： 190-198.

Li Zhiqiang， Xu Tingxue， An Jin， et al. Common Cause Failure Modeling for Redundant System Based on Dynamic Bayesian Network[J]. Chinese Journal of Scientific Instrument， 2018， 39（3）： 190-198. （in Chinese）

[54] Nguyen S， Chen S L， Du Y Q， et al. A Quantitative Risk Analysis Model with Integrated Deliberative Delphi Platform for Container Shipping Operational Risks[J]. Transportation Research Part E： Logistics and Transportation Review，? 2019， 129： 203-227.

[55] 何永昌，陳之光，王海鋒，等. 基于Netica的導彈故障診斷貝葉斯網絡模型研究[J]. 航空兵器， 2020， 27（1）： 89-95.

He Yongchang， Chen Zhiguang， Wang Haifeng， et al. Research on Bayesian Network for Fault Diagnosis of Tactical Missile Using Netica[J]. Aero Weaponry， 2020， 27（1）： 89-95. （in Chinese）

[56] Cao W B， Jia X S， Hu Q W， et al. A Literature Review on Selective Maintenance for Multi-Unit Systems[J]. Quality and Reliabi-lity Engineering International， 2018， 34（5）： 824-845.

[57] 王少華，張仕新，李勇，等. 不完全維修條件下復雜系統的選擇性維修決策方法研究[J]. 兵工學報， 2018， 39（6）： 1215-1224.

Wang Shaohua， Zhang Shixin， Li Yong， et al. Research on Selective Maintenance Decision-Making Method of Complex System Considering Imperfect Maintenance[J]. Acta Armamentarii， 2018， 39（6）： 1215-1224. （in Chinese）

[58] 王少華，張仕新，李勇，等. 有限任務間隔時間內的裝備選擇性維修決策研究[J]. 系統工程與電子技術， 2018， 40（11）： 2611-2616.

Wang Shaohua， Zhang Shixin， Li Yong， et al. Research on Selective Maintenance Decision-Making of Equipment Given Finite Mission Time Intervals[J]. Systems Engineering and Electronics， 2018， 40（11）： 2611-2616. （in Chinese）

[59] 陳一明，姜濤，劉宇. 選擇性維護決策的研究進展與挑戰[J]. 運籌學學報， 2019， 23（3）： 27-46.

Chen Yiming， Jiang Tao， Liu Yu. Selective Maintenance Optimization： Research Advances and Challenges[J]. Operations Research Transactions， 2019， 23（3）： 27-46. （in Chinese）

[60] Shahraki A F， Yadav O P， Vogiatzis C. Selective Maintenance Optimization for Multi-State Systems Considering Stochastically Dependent Components and Stochastic Imperfect Maintenance Actions[J]. Reliability Engineering & System Safety， 2020， 196： 106738.

[61] Liu Y， Chen Y M， Jiang T. On Sequence Planning for Selective Maintenance of Multi-State Systems under Stochastic Maintenance Durations[J]. European Journal of Operational Research， 2018， 268（1）： 113-127.

[62] 曹文斌，賈希勝，胡起偉. 共因失效條件下多狀態系統選擇性維修優化[J]. 航空學報， 2018， 39（2）： 164-178.

Cao Wenbin， Jia Xisheng， Hu Qiwei. Selective Maintenance Optimization for Multi-State Systems Subject to Common Cause Failures[J]. Acta Aeronautica et Astronautica Sinica， 2018， 39（2）： 164-178. （in Chinese）

[63] Chaabane K，? Khatab A，? Diallo C， et al. Integrated Imperfect Multimission Selective Maintenance and Repairpersons Assignment Problem[J]. Reliability Engineering & System Safety， 2020， 199： 106895.

[64] Jiang T， Liu Y. Selective Maintenance Strategy for Systems Executing Multiple Consecutive Missions with Uncertainty[J]. Reliability Engineering & System Safety， 2020， 193： 106632.

[65] Liu Y， Chen Y M， Jiang T. Dynamic Selective Maintenance Optimization for Multi-State Systems over a Finite Horizon： A Deep Reinforcement Learning Approach[J]. European Journal of Operational Research， 2020， 283（1）： 166-181.

[66] Schneider K， Cassady R. Evaluation and Comparison of Alternative Fleet-Level Selective Maintenance Models[J]. Reliability Engineering & System Safety， 2015， 134： 178-187.

[67] Yang D Z， Wang H C， Feng Q， et al. Fleet-Level Selective Maintenance Problem under a Phased Mission Scheme with Short Breaks： A Heuristic Sequential Game Approach[J]. Computers & Industrial Engineering， 2018， 119： 404-415.

[68] 逯程，徐廷學，李啟超，等. 競爭失效條件下的裝備選擇性維修優化方法[J]. 中國慣性技術學報， 2019， 27（2）： 272-280.

Lu Cheng， Xu Tingxue， Li Qichao， et al. Optimal Method for Selective Maintenance of Equipment Subject to Competing Failure[J]. Journal of Chinese Inertial Technology， 2019， 27（2）： 272-280. （in Chinese）

Research Advances and Challenges of Reliability Assessment of

Complex Equipment Based on Small Sample Failure Data

Li Zhiqiang1*，Wang Xin1，Chen Yuqi2，Gu Junyuan2

（1. Unit 91388 of PLA，Zhanjiang 524024， China; 2. Navy Aviation University， Yantai 264001， China）

Abstract： With the development of complex equipment which integrates mechanical， electrical， hydraulic and other technologies towards the direction of high reliability， long life and high cost， small sample failure data， even no failure data， appears in the reliability timing censoring test frequently. On the basis of explaining the characteristics of machine-level and system-level complex equipment with multi-source reliability data， uncertain data information， and continuous execution of tasks， this paper summarizes the research status of reliability evaluation of small sample failure data from three aspects of prior information， data expansion and multi-source information fusion. The shortcomings of the existing research are summarized， and the development trend and research focus of reliability assessment of complex equipment in the future are put forward. A new idea of applying Bayesian network to quantify the uncertainty in complex equipment is proposed， and the research of selective maintenance optimization on group equipment based on reliability assessment is carried out.

Key words： small sample; reliability assessment; uncertainty; Bayesian network; selective maintenance

收稿日期：2020-06-25

基金項目：國家自然科學基金項目（51605487）

作者簡介：李志強（1988-），男，四川宜賓人，工程師，博士，研究方向為武器裝備可靠性試驗與評估。