雙口形式的戴維寧定理在電路分析中的應用

梁永清, 龔文英, 李畸勇

(廣西大學電氣工程學院 廣西大學電氣工程國家級實驗教學示范中心， 廣西 南寧 530004)

0 引言

電網絡理論是電氣專業學生的必須掌握的分析工具。在電路分析中常用的方法有回路電流法、節點電壓法、疊加定理、戴維寧定理等，這些方法通常只針對單端口電路，對多端口網絡則較少涉及。隨著大規模電網絡的出現，常規求解方法已不能滿足需要。面對現代電子或電力技術中包含大量元件的大規模電路，矩陣分析法成為行之有效的分析手段。

單端口戴維寧定理描述為：任一線性含源單口電路，可等效為一個電壓源與電阻串聯的等效電路。電壓源的電壓Uoc等于端口開路電壓，電阻Req為電路獨立源置零后的等效電阻[1～2]。實際上可將戴維寧定理的應用推廣為雙口網絡。

網絡撕裂算法，包括支路撕裂法和節點撕裂法兩類。其基本思想是把復雜網絡分解成子網，對各子網在分割邊界處分別進行等值計算，求出分割邊界處的協調變量[1]。分塊計算可以提高計算效率。二端口網絡又稱雙口網絡，是多端口網絡中最常見的一種形式，電工電子技術中很多實際問題都可以利用雙口理論進行研究。本文基于支路撕裂法，探討雙口形式的戴維寧定理及其在電路分析中的應用，供大家參考。

1 基于雙口網絡的戴維寧定理

1.1 撕裂網絡

為敘述方便，本文討論的有源雙口網絡是指含獨立源的二端口網絡。無源雙口網絡是指不含獨立源的二端口網絡。用撕裂法將電路網絡分解為共地連接的有源雙口網絡N和無源雙口網絡L的組合形式，如圖1所示。構造為戴維寧定理雙口等效網[1～2]，如圖2所示。

圖1 雙口網絡

圖2 戴維寧定理雙口等效網絡

(1)

ZL為無源雙口負載阻抗，其Z參數為

(2)

1.2 雙口網絡的戴維寧定理的矩陣形式

由圖2，設端子A、B、M、N的對地電壓分別為UA、UB、UM、UN

則UA=ZL11IL1+ZL12IL2

(3)

UB=ZL21IL1+ZL22IL2

(4)

UM=-ZO11IL1-ZO12IL2

(5)

UN=-ZO21IL1-ZO22IL2；

(6)

UO1=UA-UM=(ZL11+ZO11)IL1+(ZL12+ZO12)IL2

(7)

UO2=UB-UN=(ZL21+ZO21)IL1+(ZL22+ZO22)IL2

(8)

(9)

即UO=(ZO+ZL)IL

(10)

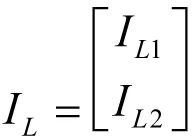
(11)

1.3 有源雙口網絡撕裂原則：

由圖1, 沿A、B處撕裂，撕裂后的有源雙口網絡N應滿足：

(1)各節點電流遵循KCL，各回路電壓遵循KVL定律。

(2)無伴電壓源(包括無伴受控電壓源)不能短路，無伴電流源(包括無伴受控電流源)不能開路。且受控源的控制量不能被消去。

(3)對于多電源電路，各無伴電壓源(包括無伴受控電壓源)不能并聯，各無伴電流源(包括受控電流源)不能串聯。

(4)ZL與N無耦合關系。

1.4 無源雙口阻抗參數

為求解方便，設ZL為不含受控源的雙口無源網絡。電路中常見的類型有T型網絡、V型網絡和Δ型網絡。

雙口T型網絡如圖3所示，其Z參數為：

(12)

雙口V型網絡如圖4所示，其Z參數為：

(13)

對于圖5所示的雙口Δ型網絡，可利用Y/Δ變換將其變換為雙口T型網絡，再求其Z參數。

圖3 T型網絡

圖4 V型網絡

圖5 Δ型網絡

2 雙口戴維寧定理在獨立電源電路中應用

算例1：計算圖6所示電路中電流IL1和流IL2

圖6 算例1原電路

解：將原電路(圖6)中由R1、R2、R3組成的T型電阻作為雙口負載阻抗，沿A、B處撕裂，分解為有源雙口網絡(圖7)和雙口負載阻抗(圖9)的組合。

1)計算開路電壓

由圖7得，UO1=136-2×3=130 V，UO2=50 V

(14)

(15)

2)計算有源雙口網絡的內阻抗Z參數

(16)

3)計算雙口負載阻抗的Z參數

(17)

4)列寫雙口網絡戴維寧定理的矩陣形式

由式(9)、(10),UO=(ZO+ZL)IL得

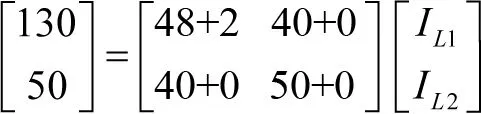
(18)

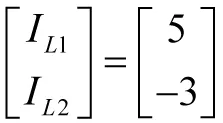
(19)

圖7 撕裂后有源雙口網絡

圖8 有源雙口網絡的內阻抗ZO

圖9 雙口T型負載阻抗ZL

3 雙口戴維寧定理在含受控源電路中應用

對于含受控源電路，除了遵循獨立電源電路的規則外，還應注意受控源的控制量不能為端口電流或電壓；求有源雙口網絡的內阻抗Z參數時，應將所有獨立電源置零(電壓源短路，電流源開路)，受控源應保留，其控制量不能被消去。

撕裂后的有源雙口網絡N與無源雙口內阻抗ZO應滿足的條件：

1)含有受控電壓源電路

①無伴受控電壓源不能與無伴電壓源并聯；②無伴受控電壓源不能短路，且控制量所在支路不能與之并聯。

2)含有受控電流源電路

①無伴受控電流源不能與無伴電流源串聯；②無伴受控電流源不能開路，且控制量所在支路不能與之串聯。

算例2：計算圖10所示電路中電流IL1和IL2

圖10 算例2原電路

解：本例屬于含有一個受控電壓源電路。將原電路(圖10)中由R1、R2組成的V型電阻作為雙口負載阻抗，沿A、B處撕裂，分解為有源雙口網絡(圖11)和雙口負載阻抗(圖13)的組合。

1)計算開路電壓

由圖11得，I=9-17=-8 A，UO2=-16 V，

(20)

UO1=UO2+33I=-280 V，

(21)

(22)

2)計算有源雙口網絡的內阻抗Z參數

將圖11有源雙口網絡中獨立電源置零，受控源保留，得圖12。

圖11 撕裂后有源雙口網絡

圖12 有源雙口網絡的內阻抗ZO

當I2=0，UI=2I+33I=35I，

(23)

I1=I，U2=2I

(24)

(25)

當I1=0，I2=I，UI=35I=35I2，U2=2I=2I2

(26)

(27)

(28)

3)計算雙口負載阻抗的Z參數

(29)

圖13 雙口V型負載阻抗ZL

4)列寫雙口網絡戴維寧定理的矩陣形式

由式(9)、(10)，UO=(ZO+ZL)IL得

(30)

(31)

4 結語

戴維寧定理作為經典理論，在電學中的地位舉足輕重。本文基于雙口網絡的戴維寧定理，通過算例嘗試性地進行了分析與探討。本方法并不針對所有電路，只適用于滿足約束條件的電路網絡。要成功運用該方法，必須遵循撕裂原則。通過撕裂法，合理地分解網絡并正確求出其參數是關鍵，否則會造成無解。負載之所以選擇V型或T型雙口網絡，是因為撕裂后的網絡“破壞性小”，而且計算簡單。特別是含受控源電路，控制量耦合關系復雜，既要解出撕裂后有源雙口網絡的開路電壓，又要解出無源雙口網絡的Z參數。該方法對豐富電路理論知識，提高學生分析問題的能力是有所幫助的。