振動磨機環扇形激振板的橫向振動與穩定性分析
楊勇強,張 曼
(陜西科技大學機電工程學院,陜西 西安 710021)
1 引言
振動磨機是一種礦產試樣破碎加工的主要設備。振動磨機的原理是利用特殊研磨介質和礦料之間的相互碰撞、擠壓和摩擦將礦料制成粉狀。國內外學者對振動磨機進行了一定的研究。文獻[1]采用有限元法進行了振動磨機的振動特性分析,得到了振動磨機整體的工作頻率控制方法。文獻[2]建立了離散磨介群動力學模型,計算獲得研磨介質質點的速度、加速度以及應力應變的變化情況。文獻[3]以振動強度和撞擊力最大,研磨介質體積最小為優化目標,采用多目標遺傳算法對立式振動磨機關鍵結構參數進行了多目標優化設計。上述研究主要針對振動磨機整機工作及研磨介質進行了分析,對其激振機構的研究較少。一種小型立式振動磨機,其核心部位為環扇形機構,如圖1所示。該環扇形機構高速旋轉產生激振力促使缽體產生振動,實現磨料工作。立式振動磨機的激振力、振動頻率和振幅等參數與環扇形機構的結構和運動速度等因素有關[4],環扇形激振機構的橫向振動對振動磨機的整機運轉產生較大影響,因此研究振動磨機環扇形機構的運動穩定性具有重要的理論意義。
近年來,許多學者對環扇形板橫向振動問題進行了一定的研究分析。文獻[4]利用有限元法分析了功能梯度扇形板的非線性自由振動問題。文獻[5]在建立統一旋轉結構動力學模型的基礎上,分析了復雜邊界條件下扇形板和類扇形板的自由振動問題。文獻[6]在平面線彈性理論基礎上,建立了環扇形板面內自由振動運動方程,并計算獲得其自由振動的無量綱固有頻率。以上動力學研究均未研究旋轉角速度對環扇形板橫向振動的影響,事實上,旋轉角速度對其橫向振動影響較大。基于此,本文以振動磨機的環扇形激振板為研究對象,對其在一定旋轉角速度情況下的橫向振動進行分析,并研究其運動穩定性問題。
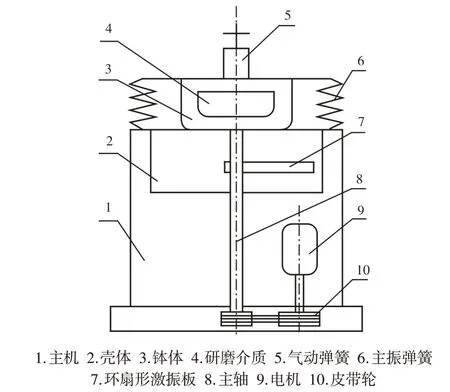
圖1振動磨機示意圖Fig.1 Sketch of Vibration Mill
2環扇形板運動微分方程的建立
該小型振動磨機的環扇形激振機構,如圖2(a)所示。其結構可簡化為環扇形板,如圖2(b)所示。圖中:h—環扇形板的板厚為,b—外半徑,a—內半徑,?—扇形角,Ω—旋轉角速度。
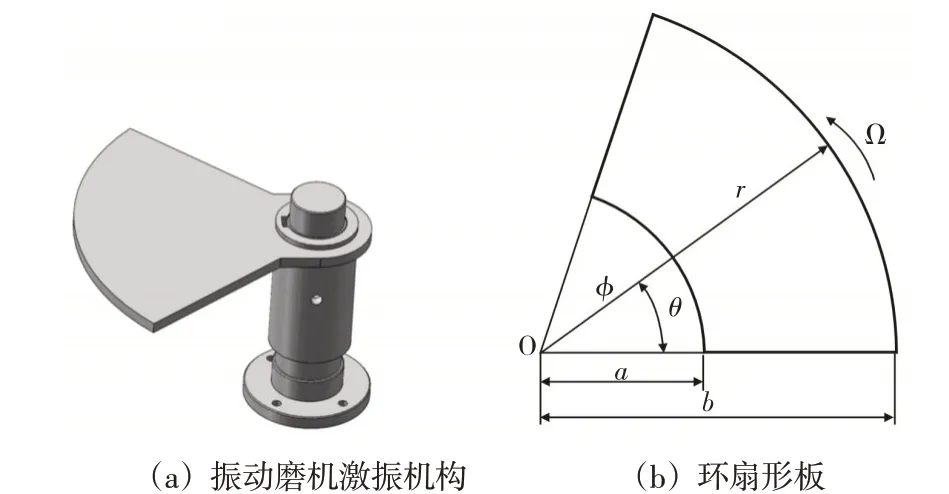
圖2振動磨機環扇形激振板Fig.2 Annular Sector Excitation Plate of Vibration Mill
根據哈密頓原理,環扇形板橫向振動運動微分方程為[7]:
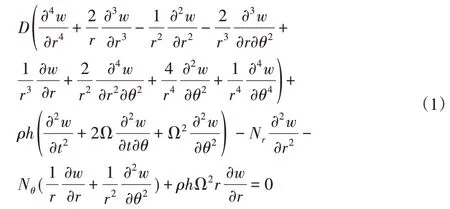
式中:w—橫向撓度,抗彎剛度,E—彈性模量,μ—泊松比,N r和Nθ—環扇形板單位寬度的徑向和環向拉壓力,ρ—材料密度。
根據彈性小撓度薄板理論,利用平衡微分方程、物理方程和相容方程可得[8]:

式中:u r—環扇形板中面的徑向位移;A和B—積分常數,與環扇形板的邊界條件有關。外徑邊界條件為自由,即。根據邊界條件計算A和B,得到環扇形板拉壓力分別為:
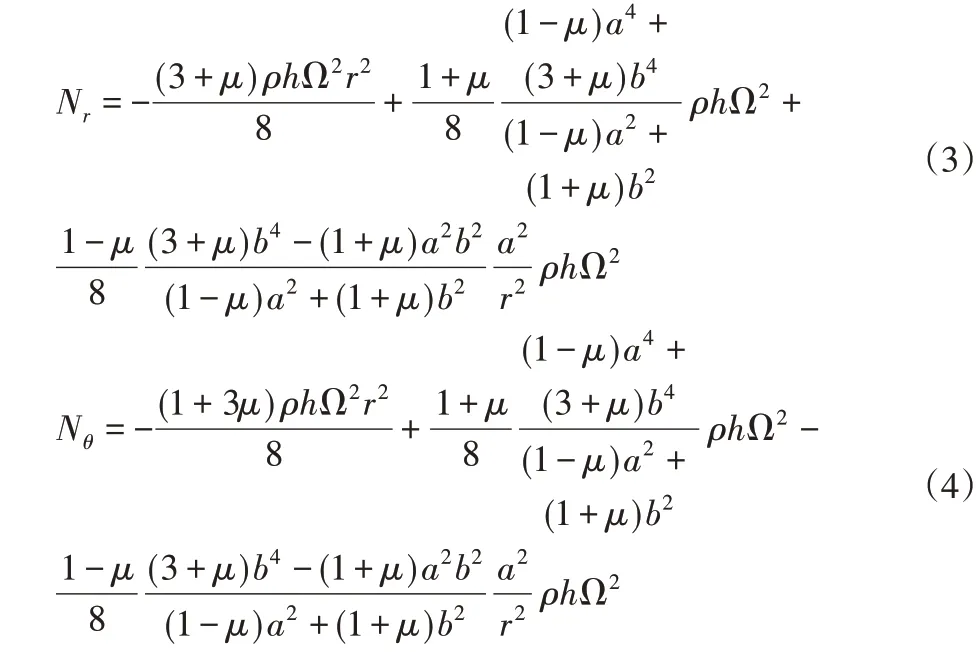
3運動微分方程及邊界條件無量綱化
引入下列無量綱量:
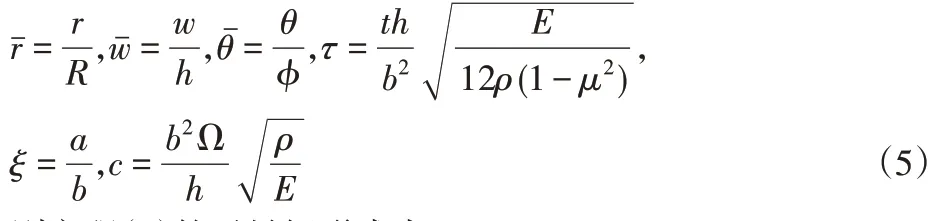
則方程(1)的無量綱形式為:
環扇形板拉壓力無量綱化分別為:
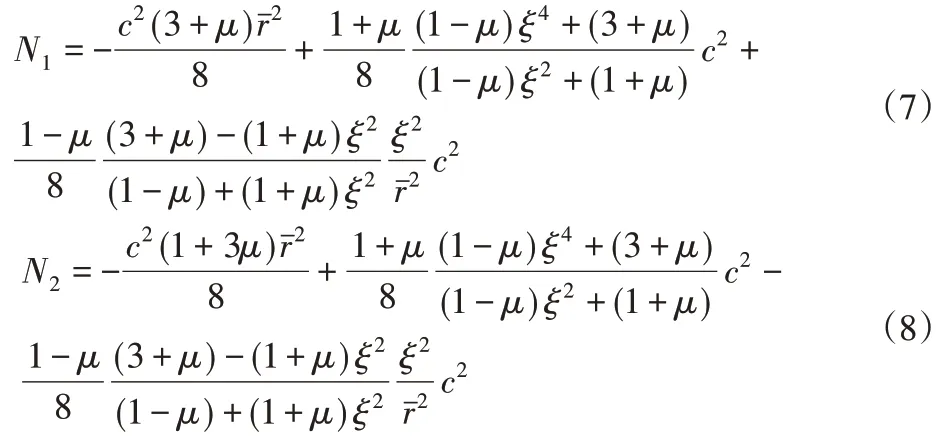
設方程(6)的解為:

式中:ω—無量綱振動頻率,j= -1。
將式代(9)入方程(6),得到環扇形板的運動微分方程為:
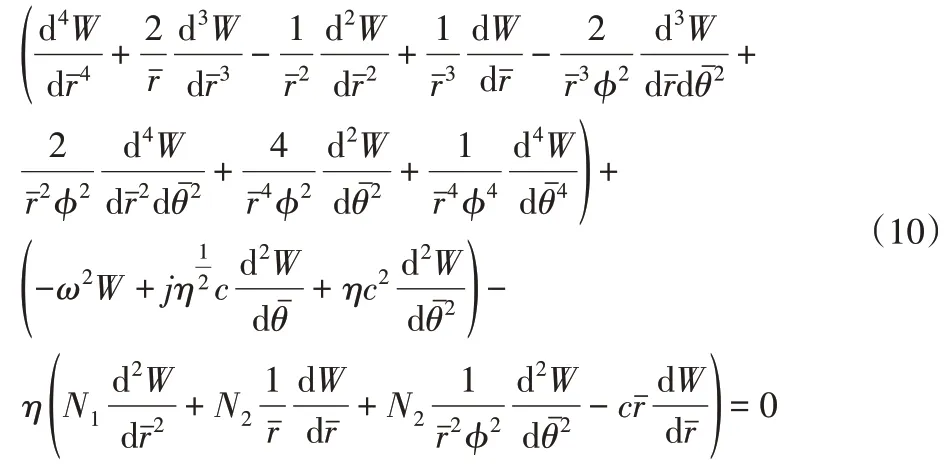
環扇形板內外徑處的無量綱邊界條件為:

4 微分求積法求解
利用微分求積法在環扇形板的徑向和環向區域內取若干節點,則節點的橫向振動函數值W及其各階導數可用其函數值加權求和來表示。徑向節點劃分采用節點替代法(即δ法)進行非均勻劃分,其計算公式為:
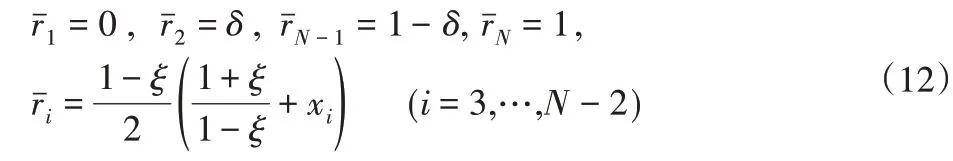
根據參考文獻[9-10],徑向一階導數權系數
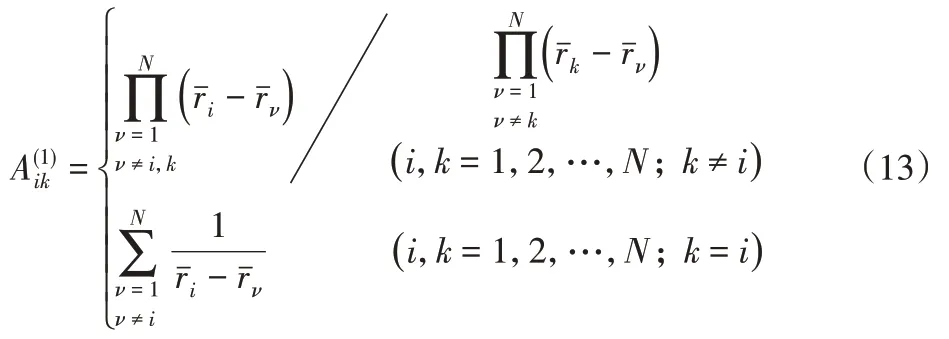
徑向高階導數的權系數可以通過矩陣相乘求得,即:

環向節點劃分及函數各階導數B(kmj)權系數矩陣與上述徑向情況類似,這里省略。采用微分求積法法離散化振動方程(10),其微分求積法形式為:
式(15)和(16)的微分求積形式聯立得到的矩陣形式為:
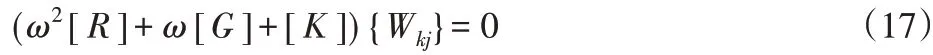
其中,矩陣[R],[G]和[K]中含有環扇形板的半徑比、扇形角以及無量綱角速度等參數,式(17)構成了廣義特征值問題。因此,振動磨機環扇形板的特征方程表達為:

5 無量綱復頻率隨無量綱角速度變化的數值計算與分析
根據磨料工況不同,該小型振動磨機環扇形板的半徑比為ξ=0.25,0.305(內半徑為55 mm,外半徑為220mm,180mm),扇形角?分別為π4和π2。以下對不同半徑比和扇形角情況下的環扇形板無量綱復頻率進行計算分析。
當半徑比ξ=0.25,扇形角?=π4時,旋轉環扇形板前四階模態無量綱復頻率隨無量綱角速度的變化情況,如圖3所示。由圖3可知,當無量綱角速度c=0,環扇形板自由振動的無量綱固有頻率ω為實數。隨著無量綱角速度c的增加,前四階無量綱復頻率Re(ω)實部為正值,虛部Im(ω)保持為零,表明板處于穩定狀態。當c=0.72時,第1階模態復頻率實部Re()ω=0,而虛部Im()ω分為正負兩個分支,說明環扇形板出現第1階模態發散失穩。無量綱臨界角速度c=0.72即為第1階臨界發散角速度。當c=0.96時,板又恢復穩定。當c=1.44時,第1階和2階模態發生顫振耦合;當c=0.90時,第3階和4階模態也發生顫振耦合。c=1.44和c=0.90分別為第1、2階臨界顫振角速度和第3、4階臨界顫振角速度。

圖3 前四階無量綱復頻率隨無量綱角速度變化曲線(ξ=0.25,?=π4)Fig.3 First Four Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed(ξ=0.25,?=π 4)
當半徑比ξ=0.305,扇形角?=π4時,旋轉環扇形板前四階模態無量綱復頻率隨無量綱角速度的變化情況,如圖4所示。由圖4可知,當c=1.04時,環扇形板出現第1階模態發散失穩,第1階臨界發散角速度c=1.04大于圖3所示的第1階臨界發散角速度。當c=1.22時,板又恢復穩定狀態。與ξ=0.25,?=π4情況不同在于,環扇形板并沒有發生第1階和2階顫振耦合失穩,僅僅出現了第3、4階模態耦合失穩,相應的第3、4階臨界顫振角速度為c=0.48。
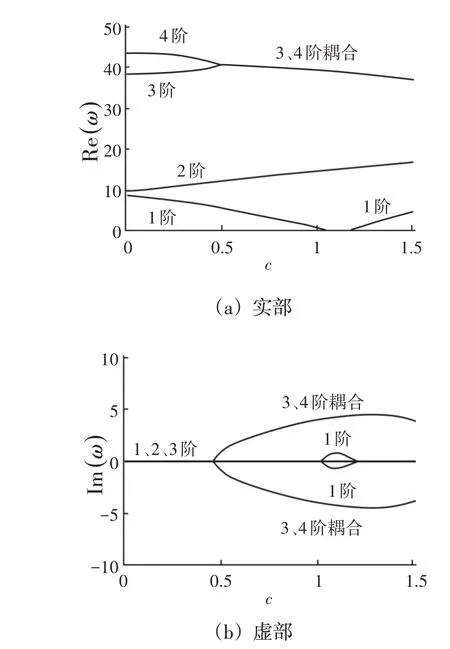
圖4 前四階無量綱復頻率隨無量綱角速度變化曲線(ξ=0.305,?=π4)Fig.4 First Four Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed(ξ=0.305,?=π4)
當半徑比ξ=0.25,0.305,扇形角?=π4時,旋轉環扇形板前三階模態無量綱復頻率隨無量綱角速度的變化情況,如圖5和6所示。由圖5、圖6可以看出,隨著無量綱角速度c的增加,環扇形板均發生第1階發散失穩現象以及第2階和3階顫振耦合現象。對比圖5、圖6,在半徑比ξ=0.305,扇形角?=π4情況下,當c=0.98時,旋轉環扇形板第2和3階模態的無量綱復頻率實部Re(ω)分為兩支,虛部Im(ω)為零,說明板在發生顫振耦合失穩之后又重新恢復穩定。同時,ξ=0.305情況下的第1階臨界發散角速度大于ξ=0.25情況下的第1階臨界發散角速度
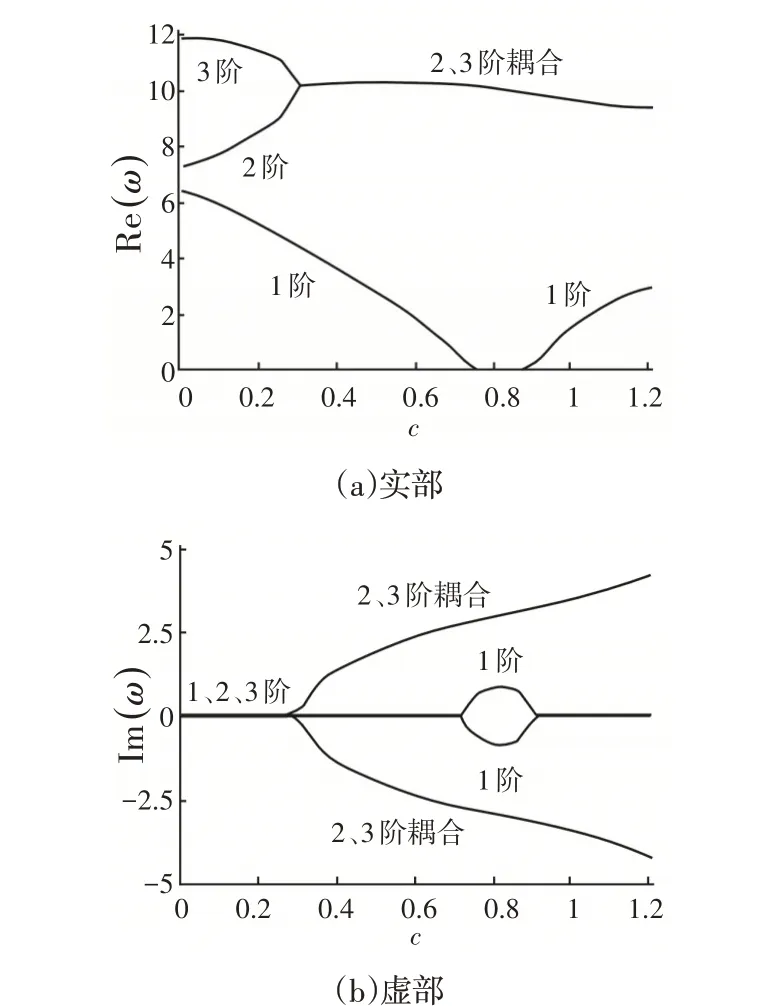
圖5 前三階無量綱復頻率隨無量綱角速度變化曲線(ξ=0.25,?=π2)Fig.5 First Three Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed(ξ=0.25,?=π 2)
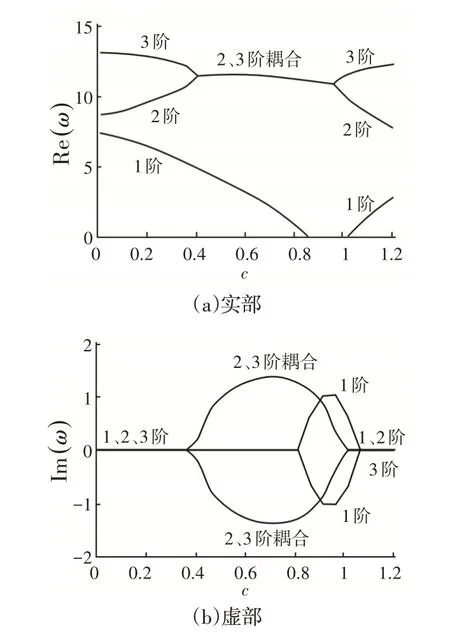
圖6 前三階無量綱復頻率隨無量綱角速度變化曲線(ξ=0.305,?=π2)Fig.6 First Three Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed(ξ=0.305,?=π2)
6 結論
采用微分求積法對振動磨機旋轉環扇形激振板的橫向振動和穩定性問題進行了分析,得到了旋轉環扇形板的前三(或四)階復頻率的實部和虛部隨旋轉角速度的變化情況。分析結果表明,隨著無量綱角速度的增加,振動磨機環扇形板發生第1階模態發散失穩現象和其它階模態的顫振耦合失穩現象,顫振耦合失穩現象發生的模態階數與環扇形板的半徑比和扇形角有關。上述結果為振動磨機激振系統的設計與研究提供了一定的參考依據。

