基于單純形優化算法的火箭彈增程研究

張 斌，陳國光，王 捷

（1.中北大學，山西太原 030051；2.西南技術物理研究所，四川成都 610041）

為滿足當前遠距離、精確化、大威力的現代戰爭作戰要求，火箭彈增程技術當前已成為當前研究的熱點之一。目前，火箭彈增程方法有提高發動機總沖、改良火箭彈結構以及增添舵機控制的滑翔增程等。單就結構和推進劑的改良而言，增程效果并不佳。依據彈道修正彈彈道特性分析，采用舵機控制的滑翔增程方法不僅能有效增加射程，還能減少因火箭彈增大射程而帶來的散布問題。

滑翔增程是通過調整舵翼偏轉來控制火箭彈的升力，使火箭彈緩慢下降，進而延長飛行時間，達到增程的目的。這種增程方法是基于彈箭飛行特性提出的，對制導控制及彈道修正有著重要指導意義。經查閱文獻了解，目前增程方案有：分析增程原理和彈道特點，控制重力法向方向始終平衡的方案；采用控制火箭彈法向過載最優的方案；采用數值解算最大升阻比的思想建立滑翔段模型；以能量法研究滑翔彈道，最小能量損失的彈道設計；對滑翔段進行分段控制，保證舵偏角在每1小段都不變，探究分段次數與增程的關系；依據氣動力參數，擬合最大升阻比下的攻角隨馬赫數的變化曲線及攻角隨時間的函數，實現滑翔增程；以射程為優化變量，采用序列二次規劃優化算法，進行數值仿真；采用現代優化算法，對彈道進行全局約束搜索最優攻角方案。

目前，多采用地面雷達監測及發射指令的方式修正彈道，對于高速短時作戰的彈藥而言，這種方法存在時間誤差和預測偏差等問題，修正效果并不理想。

基于此，本文從能量法角度分析并提出了1種基于彈載計算機實時優化的改進單純形優化算法，在SIMULINK 中建立彈道模型，并將優化算法模塊化，嵌套在仿真程序中，跟隨彈道解算過程對攻角進行實時優化。通過該算法，能快速找到當前彈道諸元（速度、高度、彈道傾角等）下的最優控制量。通過仿真分析驗證了算法有效性。

1 模型建立

本文的研究對象是某型制導火箭彈，其采用雙通道舵機，卷弧尾翼。三維彈體模型，如圖1所示。

圖1 制導火箭彈模型Fig.1 Guided rocket model

對于雙通道控制舵機，升降舵和方向舵是分開控制的：升降舵主要控制火箭彈在縱向平面的射程修正；方向舵則控制水平面的偏差量修正。本文主要研究火箭彈在縱向平面的增程問題。

1.1 滑翔增程彈原理

制導火箭彈通常在彈道前期無控飛行，飛行到彈道頂點附近打開舵機，通過電機驅動舵翼偏轉，調整彈體的升力，減小或平衡彈丸在速度矢量法向方向的重力分量，從而延長飛行時間，增加飛行距離。

在彈道縱向平面內，火箭彈沿速度矢量方向的受力分析，如圖2所示。

圖2 火箭彈在速度矢量方向的受力分析Fig.2 Force analysis of rocket in the direction of velocity vector

從能量角度分析，因高度降低所產生的勢能轉化成動能和克服空氣的阻力，動能的增加勢必加快高度的降低，這對增程而言是不利的。因此，將勢能盡可能地用來克服空氣阻力，維持動能不變或緩慢減小是1種增加射程的有效方法。

由圖2受力分析可知，速度是由切向合力控制，高度的降低是由空氣作用力和重力兩者的合力控制。控制速度變化的切向合力最小，以及控制彈道傾角變化的法向合力最小，即可達到緩慢下降及速度緩慢減小的目的。將上述理論轉化為數值表達式，為更易實現這一方法，采用標量的合力之和來替換矢量合力。為避免各合力出現負值的情況，對各合力做絕對值運算。整合以上理論，如式（1）：

式（1）中：

X

為空氣阻力；

Y

為空氣升力；

m

為火箭彈質量；

θ

為彈道傾角；

g

為當地重力加速度，與高度

y

有關。

式（2）中：

ρ

為空氣密度；

X

為空氣阻力；

Y

為空氣升力；

S

為彈丸特征面積；

C

為零升阻力系數；

C

為誘導阻力系數；

C

′為升力系數導數；

α

為攻角。火箭彈受力隨飛行位置不斷發生變化，受飛行穩定性及修正裝置等的限制，此處的合力最小為優化問題，須通過優化方法獲取。為此，本文提出實時優化的算法以解決這一問題。將優化算法嵌套在彈載計算機程序中，每隔

T

時刻，接收并處理火箭彈的位置及速度信息，求解出采樣時刻的最優攻角值，再轉化成修正指令，控制舵翼偏轉，實現增程目的。

1.2 彈道模型及方程建模

通過對火箭彈增程原理分析，結合原火箭彈特點，總結滑翔增程火箭彈彈道特點如下。

1）主動段。該段彈丸受重力、空氣動力及發動機推力作用，受推進劑燃氣推動作用，彈丸做加速運動。發動機停止工作后，彈丸達到最大速度。

2）被動段。該段彈丸僅受空氣動力和自身重力作用，與無控彈的彈道解法一致。

3）控制段。在彈丸到達彈道頂點附近時，打開舵機。在電機驅動下，舵翼按照舵機指令進行偏轉，空氣作用力隨之發生改變，進而達到調整姿態、修正彈道的作用。

根據以上彈道特點描述，飛行彈道特性模擬圖，如圖3所示。

圖3 滑翔增程火箭彈彈道模擬圖Fig.3 Ballistic simulation diagram of glide extended range rocket

依據前文分析，本文只研究有控彈箭在縱向平面的運動，由于采用卷弧尾翼，彈丸旋轉速度會降低，飛行至控制段時近似看作無旋運動，即忽略彈箭繞質心的轉動，只研究彈箭質心的運動。由此，縱向平面可操縱質點方程組如下：

2 優化算法建模

2.1 基于單純形的攻角優化建模

單純形法（Simplex）是1962 年由Spendley、Hext和Himsworth 提出，再由Nelder 和Mead 于1965 年改進，故又稱為NM 算法。它是1 種不使用導數求解無約束極小化問題的直接搜索方法。相比最優化方法中的解析法，此法僅需要相關函數值信息，就可尋找最優解。不同于其他優化的算法，它從最初構造的單純形，不斷替換最大值點，構造更適合尋優的新單純形。基本原理如下：

在

n

維空間中，以

n

+1 個頂點構成一個單純形(

x

,

x

,

x

,…,

x

)。并將單純形中各頂點代入到目標函數中求解函數值。記各函數值中最小值為

f

(

x

)，最大值為

f

(

x

)。并求除最大值以外各點的重心，及最大值頂點關于重心的反射點，依據反射點函數值的大小選擇延伸、收縮或壓縮，得到新的較好頂點并替換原單純形中最大值頂點，構造新的單純形。通過反復求解較小點來替換新單純形中最大值頂點，迭代單純形，逼近極小值點。單純形中重心、反射點、延伸點、收縮點、壓縮點以及精度的計算公式如下：

式（4）中：

x

為單純形頂點；

x

為最大值頂點；

x

為最小值頂點；

x

為重心；

x

為反射點；

x

為延伸點；

x

為收縮點；

x

為壓縮點；

h

為反射系數；

β

為延伸系數；

γ

為收縮系數；

δ

為壓縮系數；

ε

為計算精度。

2.1.1 選取設計變量

依據公式（1）分析，為獲取采樣時刻最優攻角，實時彈道優化以采樣時刻彈道諸元作為優化輸入量，以平衡攻角為優化變量。隨采樣時刻的更新進行實時優化。設計變量

Γ

見式（5）。

式（5）中：

y

為火箭彈采樣時刻高度；

v

為采樣時刻速度；

θ

為采樣時刻彈道傾角；

ρ

為采樣時刻空氣密度；

g

為采樣時刻的重力加速度；

α

為采樣時刻待優化的攻角。

2.1.2 建立目標函數

基于公式（1）分析，將采樣時刻的位置和速度信息作為優化輸入量，以采樣時刻合力最小值為目標函數。結合式（1），目標函數

F

見式（6）：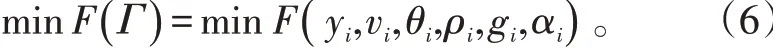

2.1.3 添加參數約束

攻角的取值，取決于彈箭物理參數及舵機的修正能力，更重要的是不能影響飛行穩定性，這限制了攻角只能在一定范圍內變化，見式（7）：

式（7）中：

α

為攻角最小值；

α

為攻角最大值。

2.1.4 算法終止條件

單純形算法優點是尋優效率高，能快速迭代到最優解附近；缺點是在最優點附近收斂速度較慢。而實時修正的核心即時效性，短時多修，因此對于精度要求并不是很高。為了更好滿足實時解算要求，縮短算法終止時間，本文在原算法基礎上再增添終止條件，以連續3 次輸出迭代優化值之差小于迭代誤差

ε

作為終止條件。雙重終止條件能有效縮短迭代時間。迭代誤差

ε

見公式（8）：

式（8）中：

ε

為迭代誤差；

x

為第

i

次迭代結果；

x

為第

i

-1次迭代結果。

2.1.5 單純形法優化攻角流程

1）設定控制段采樣時刻

T

=0.1 s，獲取采樣時刻的火箭彈位置和速度信息。統一設定待優化的攻角初始值為0。并設定優化函數中的參數值：初始步長、反射系數、收縮系數、壓縮系數及計算精度。

2）將初始攻角值及采用初始步長獲取的新攻角值代入插值函數中，分別插值計算出當前攻角及馬赫數下的氣動力參數，并將氣動力參數值代入目標函數中，求解當前目標函數值。

3）將2）中得到的目標函數值返回到優化算法中，確定最小值頂點

x

及最大值頂點

x

，并計算重心、反射點。4）通過對反射點的函數值求解，選擇延伸處理、收縮處理或壓縮處理。使目標函數更小的點為新的單純形頂點，返回并替換步驟3）中的

f

( )

x

，重新確定新單純形的最大值頂點及最小值頂點，重復以上步驟，反復迭代新單純形，直至滿足計算精度為止。

5）將優化算法得到的攻角值與式（6）比對，將不在攻角設定范圍的攻角值進行輸出限制或替換。最后輸出攻角，作為當前火箭彈飛行的控制量。直至得到下1 個最優攻角。通過這種交替優化解算方法，獲取控制全段的最優攻角值。

2.2 SIMULINK建模仿真

工程上常用C語言求解彈道，這對編程能力要求高。SIMULINK 是將MATLAB 的相關函數進行模塊化封裝，對使用者來說要求低、易上手，對于所有設定的參數均可實時讀取，通用性高，可視性強，已成為學者和工程師求解彈道的常用軟件。本文采用SIMULINK 仿真平臺進行滑翔增程火箭彈模型建立與仿真分析。

依據滑翔增程彈的彈道特性，整個彈道模型由彈道初始模塊、氣象標準模塊、氣動力模塊、彈道方程組模塊、優化算法模塊組成。各模塊內部以子模塊或函數組成。滑翔增程火箭彈彈道解算框圖，如圖4所示。

圖4 滑翔增程火箭彈彈道解算框圖Fig.4 Diagram of ballistic calculation for glide extended range rocket

2.2.1 彈道初始化模塊

在SIMULINK中設置滑翔增程火箭彈的參數，見表1。

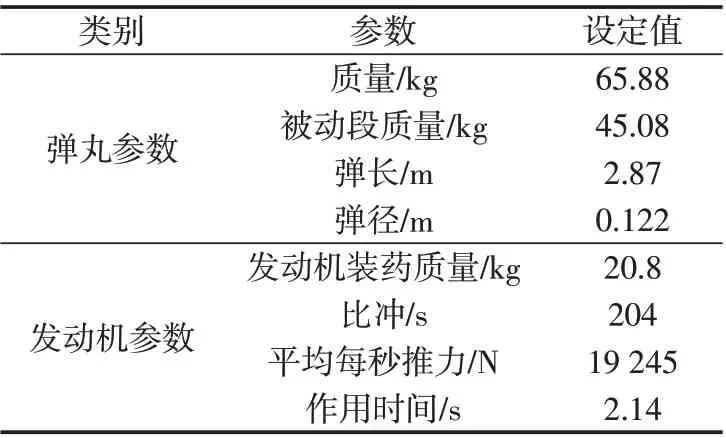
表1 火箭彈參數Tab.1 Rocket parameters

2.2.2 NM優化算法模塊

依據算法，將函數的所有輸入的參數封裝到函數模塊中，該函數模塊包括3 個函數：氣動力插值函數，目標函數及單純形優化函數。NM子模塊中的單純形優化算法函數模型，見圖5所示。

圖5 單純形優化算法函數模塊Fig.5 Function module of simplex optimization algorithm

本文火箭彈模型，依據舵機修正能力及飛行穩定性，設定攻角取值范圍為[0 °,8°] 。單純形優化算法是一種無約束優化，對于優化結果超出優化變量約束范圍的，將以攻角最值輸出。也就是優化結果大于8°則取8°，小于0°則取0°。

2.2.3 氣動力參數模塊

本文采用DATCOM 軟件獲取滑翔增程火箭彈的氣動參數。將建好的滑翔火箭彈模型的彈體參數（見表1）及舵機參數編制文件，設定不同馬赫數和攻角值，分別計算原火箭彈氣動參數，以及添加舵機后的滑翔火箭彈的氣動參數。根據滑翔增程火箭彈彈道特點，在主動段和被動段使用無舵翼氣動力參數，打開舵機后使用有舵翼的氣動力參數。

3 仿真結果及分析

由于滑翔增程彈的舵機是在頂點附近打開的，因此彈道的主動段和被動段均與原火箭彈相同。忽略無控段受外部隨機干擾造成的攻角變化，采用零攻角仿真無控段。本文采用SIMULINK 自帶算法（ode45），四階龍格庫塔解算彈道。

設定滑翔增程火箭彈初始條件是：

θ

=50°，

v

=50 m/s，

x

=0，

y

=0。將初始條件設置到SIMULINK模塊中，設置積分步長與采樣時刻同為0.1。設置程序終止條件為

y

＜0。優化函數算法中各參數取值分別為：初始步長

h

=2，延伸系數

β

=2，收縮系數

γ

=0.5，壓縮系數

δ

=0.5，計算精度

ε

=0.05，迭代終止精度

ε

=0.001。

考慮到火箭彈飛行中受到（風等）擾動，以及彈載計算機獲取的位置坐標誤差及地磁測量姿態誤差等因素，轉化各種誤差因素為攻角的響應白噪，即在實時優化后的攻角值上隨機添加[ ]-0.2°,0.2° 的偏差量。

圖6為零攻角下原火箭彈的彈道曲線。圖7為有噪與無噪的優化彈道對比圖。圖8為有噪和無噪的優化攻角對比圖。圖9 為實時攻角下的優化目標函數值。圖10是在原單純形算法下，對不同采集時刻的彈道信息分別進行實時優化的迭代次數與優化攻角的對比圖。

圖6 零攻角火箭彈彈道Fig.6 Ballistic curve of the rocket at zero angle of attack

圖7 實時優化后的彈道Fig.7 Ballistic curve of the rocket after real-time optimization

圖8 實時優化后的火箭彈攻角Fig.8 Angle of attack of the rocket after real-time optimization

圖9 實時優化下的目標函數值Fig.9 Objective function value under real-time optimization

圖10 不同時刻下迭代次數與優化結果Fig.10 Number of iterations and optimization results at different moments

圖6、7 對比表明，在射角50°、零攻角下的原無控火箭彈的射程僅22 000 m。而采用本文提出的改進單純形優化算法解算實時攻角，無噪射程為38 344.87 m ，有噪射程為38 205.04 m ，偏差僅139.83 m，無噪下增程率達到74.3%。說明此優化方法能有效增加火箭彈的射程。

圖7～9表明，在相同初始條件下，無噪和有噪解算結果相差甚小，實時解算具有較高的抗噪性。實時解算的最優攻角變化平穩，并無大的突變，對于舵機修正而言，易于實現。此改進算法能有效地應用于彈載計算機上。

圖10 表明，雖然達到原算法的計算精度，但迭代次數較多，耗時較長，不利于快速多次的實時修飛理念。

通過表2 的數據比對，原算法實時求解的時間較長，從而使舵機修正的時間間隔延長。而隨著修正間隔時間的增加，精度必然降低。采用改進后的算法，迭代次數更少，而且優化結果與原算法相差較小。改進算法能有效地縮短間隔時間，增加修正次數，更能滿足實時解算的要求。

表2 原算法和改進算法尋優結果對比Tab.2 Comparison of optimization results between the original algorithm and the improved algorithm

4 結論

針對火箭彈增程問題，在理想滑翔狀態理論基礎上，分析并提出了基于改進單純形算法的實時優化攻角的增程方法，通過在SIMULINK仿真平臺上建立彈道模型并仿真分析，得出以下結論：

1）與無控火箭彈射程相比，基于改進單純形優化算法的增程方案使得火箭彈增程率達到74.3%；

2）改進后的單純形優化算法更適合彈載計算機實時優化。