供應中斷風險下制造商應對策略研究

孔 進， 李 芳

（上海理工大學 管理學院，上海 200093）

在經濟全球化的進程中，供應商的選擇越來越多元化，供應鏈成員之間的關系網絡也日益復雜，此時供應鏈整體網絡容易受到各種不可控因素的影響。例如，新冠疫情使得諸多外貿行業的供應鏈發生中斷，疫情嚴重時期本土的供應鏈也難以幸免，供應鏈風險管理變得愈加重要，當供應鏈發生中斷時，企業需要快速作出決策以應對供應鏈中斷帶來的損失。

有關時間敏感性供應鏈的研究中，Ivanov等[1]以澳大利亞乳制品為例來研究供應中斷產生的連鎖反應對時間敏感性供應鏈的影響。Palaka等[2]對時間敏感性供應鏈進行了研究，得到了產品價格和實際交貨期的優化決策模型。Zhang等[3]對時間敏感性供應鏈中產品的定價策略進行研究，提出了分類定價策略。李煥之[4]對云環境下的供應鏈資源共享進行了博弈分析，建立了云環境下時間敏感性資源的中斷恢復策略的博弈模型，通過模型分析發現，制造商合適的援助策略能夠縮短供應恢復時間。張雪梅等[5]考慮市場需求量具有網絡渠道交付時間敏感性，并在此基礎上研究單渠道和雙渠道的定價策略問題。謝祥添等[6]考慮市場需求量具有承諾交貨時間敏感性和隨機性，并以此建立了M/M/1決策模型。朱玉煒等[7]分析了網絡直銷渠道和傳統渠道的定價策略與時間敏感系數的關系。有關供應中斷應對策略的研究中，Iyer等[8]建立了恢復成本取決于產能恢復速度的模型，以此研究單供貨方-多需求方的供應中斷恢復問題。Kumar等[9]在供應中斷背景下，分析了零售商不同采購策略對供應鏈的影響。Li等[10]對制造商存在后備供應商的情況進行研究，分析不同程度的供應中斷風險下，制造商是否以及如何使用雙源采購策略。Berger等[11]運用決策樹模型對供應中斷風險下制造商的采購策略進行研究，研究發現，當中斷風險較低時，雙源供應模式相比單源供應模式更優。Burke等[12]比較了供應不可靠條件下的單源采購與多源采購策略。Gupta等[13]采用博弈分析的方法，對2個供應商和1個零售商在供應商出現供應中斷情況下的模型進行分析，具體分析了替代產品定價決策的變化。徐蓉[14]建立國外主供應商、國內備用供應商的雙源供應模型，并在其中引入良品率這一概念，研究國外供應商的供應中斷對供應鏈各節點產生的影響。王靜等[15]驗證了供應中斷下保留冗余產能、儲備庫存及啟用備選制造商等應對方案的可行性。李姍姍等[16]考慮發生供應中斷時，市場應對中斷可能采取以下幾種措施：自動留存訂單、等待制造商應急完成訂單、安全庫存完成訂單、取消訂單，在此情況下構建了中斷負面影響最小的最優控制模型。張廣勝等[17]基于期權理論，考慮單源主供應商、應急雙源采購及單源備用供應商3種策略。何青等[18]考慮供應鏈存在供應中斷風險，在此基礎上對制造商的后備采購策略和改善努力策略進行了比較分析。顏榮芳等[19]分析由1個制造商和1個零售商組成的雙渠道供應鏈中，在需求中斷下具有提前期的雙渠道供應鏈的風險規避問題。何璐等[20]在碳稅背景下考慮供應中斷對制造/再制造企業最優策略的影響，結果表明，平均總成本隨中斷概率的增加而變大。李新軍等[21]對由制造商、戰略供應商、備用供應商組成的供應鏈進行研究，得出使用備用供應商的臨界值。陳崇萍等[22]分析了在需求與供應不確定下的雙源供應，考慮供應商產出隨機或供應商存在中斷且產出隨機的情況，建立制造商和供應商的博弈模型。

以上有關時間敏感性供應鏈的研究多集中于定價決策，較少分析時間敏感性供應鏈的供應中斷問題，有關供應中斷方面的研究主要集中在價格敏感性供應鏈中（市場需求受價格影響），對時間敏感性供應鏈研究較少。李煥之[4]進行了時間敏感性供應鏈（市場需求受價格和時間影響）的供應中斷恢復研究，但研究是針對單供應商、單制造商的供應鏈中斷恢復。本文在上述已有研究的基礎上[1-2,4,8]，對2個制造商和2個供應商的時間敏感性供應鏈進行研究，研究發生供應中斷時，制造商1和制造商2采取何種策略更優。

1 模型與基本假設

三級供應鏈系統如圖1所示，其中，制造商1采用供應商A單源供應，制造商2采用雙源供應（無中斷風險時采用供應商A供應，中斷發生時可能啟用備用供應商B），考慮主供應商A以一定概率由于緊急事件而發生供應中斷，研究此時制造商1和制造商2應對供應中斷而采取的最優策略。

圖1 結構示意圖Fig. 1 Structure diagram

基于上述模型，假設：

a. 制造商、供應商、備用供應商均處于云環境之中，制造商1、制造商2、供應商A、供應商B信息共享。

b. 考慮制造商1和制造商2均為供應商A的重要客戶，因此，供應商A會在完成所有訂單后同一時間將貨物發送給制造商1和制造商2。

c. 制造商生產的產品具有時間敏感性，即市場需求量同時受產品價格和制造商交貨時間影響。制造商1和制造商2的需求量分別為D1(p1,T)=α1-μp1-βT，D2(p2,T)=α2-μp2-βT,μ＞0,β＞0。其中，μ為價格敏感系數，β為時間敏感系數，p1為制造商1零售價格，p2為制造商2零售價格[23]，T為產品實際進入市場的時間，α1，α2分別為制造商1、制造商2的潛在市場需求量。

d. 本文僅考慮制造商的采購成本，不考慮生產運營成本。

e. 供應商A具有產品價格低、可靠性低的特點，供應商B具有產品價格高、完全可靠的特點。

f. 供應商A發生中斷時，實際交貨時間延遲造成的損失由供應商A承擔。

g. 供應商A與制造商1和制造商2存在長期合作關系，當發生供應中斷時供應商A會主動采取措施恢復產能。

h. 考慮制造商2采用備用供應商B時，供應商B的交貨時間與供應正常情況下供應商A的約定交貨時間相同。

參數設置：

ρ表示主供應商A的供應中斷的概率，0＜ρ＜1；r表示商品的殘值，r＜w1＜w2；

c1表示供應商A的生產成本；

c2表示供應商B的生產成本；

w1表示制造商向供應商A購買產品的批發價格；

w2表示制造商向供應商B購買產品的批發價格；

c(t)表示供應商A在無援助情況下付出的供應鏈恢復成本，c(t)=t2-2Ht+F，H為供應商A允許大成本[23]；的最長交貨時間，F為供應商A可能付出的最

t表示供應商A實際交貨時間；

t0表示供應中斷發生時間；

t1表示正常情況下供應商A與制造商1、制造商2約定的交貨時間；

t2表示制造商1和制造商2生產時間，本文不考慮制造商1和制造商2生產時間差異；

(i=M,N;j=O,M,N)表示制造商1和制造商2不同策略下，供應商A的期望收益；

(i=M,N;j=O,M,N)表示3種策略下，主要供應商A的期望收益；

(i=M,N;j=O,M,N)表示3種策略下，備用供應商B的期望收益；

其中，i=M表示制造商1采用供應商A供貨但不采取援助措施，i=N表示制造商1采用供應商A供貨并采取援助措施，j=O表示制造商2采用備用供應商供貨，j=M表示制造商2采用供應商A供貨但不采取援助措施，j=N表示制造商2采用供應商A供貨并采取援助措施。

2 模型的建立與求解

發生突發事件時，供應商A產能陷入癱瘓，供應鏈發生中斷。云環境下，供應商A將中斷實際情況告知制造商1和制造商2并承諾會盡可能早地恢復生產，并征求制造商1和制造商2的意見。參考李煥之[4]關于供應鏈中斷時制造商與供應商策略的分析，同時結合本文模型，考慮當供應商A發生供應中斷時，制造商1可以采取2種策略：a. 采用供應商A供貨但不援助供應商A；b. 采用供應商A供貨并援助供應商A。制造商2可以采取3種策略：a. 采用備用供應商B供貨；b.采用供應商A供貨但不援助供應商A；c. 采用供應商A供貨并且援助供應商A。

2.1 制造商1采用供應商A供貨但不采取援助措施且制造商2采用備用供應商B供貨情形（策略1）

制造商1表示愿意繼續采用供應商A供貨但不會采取援助措施，制造商2表示將放棄供應商A并采用備用供應商B供應，制造商1和制造商2的各節點時間如圖2所示。T1=t1+t2；T2=t+t2。

圖2 時間節點示意圖1Fig.2 Schematic 1 for time node

T1表示無供應中斷情形下產品投入市場的時間，T2表示策略1中制造商1生產產品實際投入市場的時間。

考慮制造商1、制造商2、供應商A之間勢均力敵，此時供應商A、制造商1、制造商2的期望利潤函數：

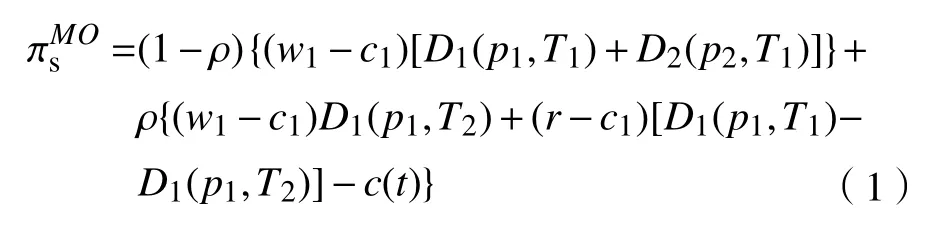
命題1存在納什均衡解，(tMO*,p1MO*,p2MO*)使得供應商A、制造商1、制造商2各自收益最大。

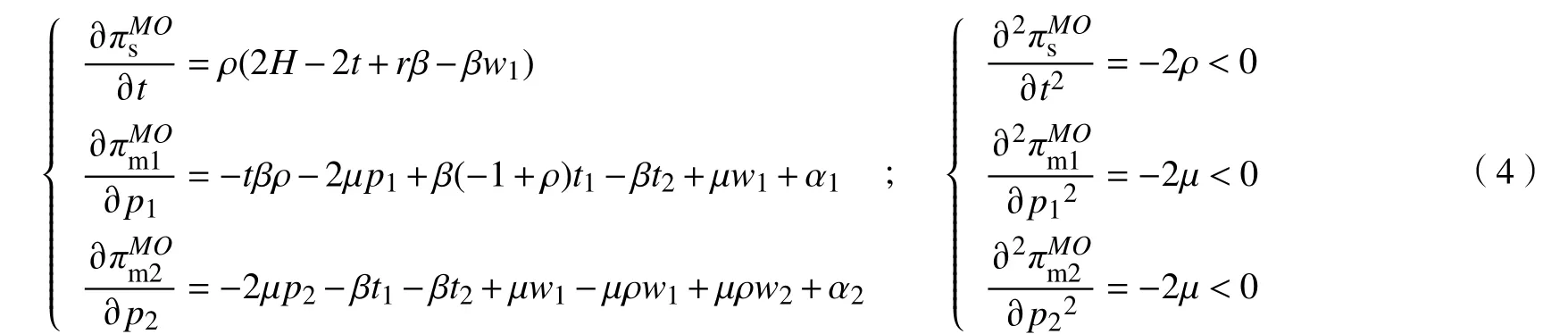
證明由式（4）可知，存在t*（在無援助策略時，tMO*=t*）使得供應商A的期望利潤最大，存在p1MO*使得制造商1的期望利潤最大，存在p2MO*使得制造商2的期望利潤最大。

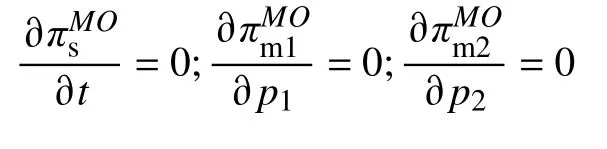
同時將代入，tMO*p1MO*p2MO*，可得

2.2 制造商1采用供應商A供貨但不采取援助措施且制造商2采用供應商A供貨但不采取援助措施情形（策略2）

制造商1表示愿意繼續采用供應商A供貨但不會采取援助措施，制造商2表示愿意繼續采用供應商A供貨但也不會采取援助措施，制造商1和制造商2的各節點時間如圖3所示。T2=t+t2。

圖3 時間節點示意圖2Fig.3 Schematic 2 for time node

考慮制造商1、制造商2、供應商A之間勢均力敵，供應商A、制造商1、制造商2的期望利潤函數：

命題2存在納什均衡解使得供應商A、制造商1、制造商2各自收益最大。

證明方法如命題1所示，本文不在作詳細證明，可得

2.3 制造商1采用供應商A供貨但不采取援助措施且制造商2采用供應商A供貨并采取援助措施情形（策略3）

制造商1表示愿意繼續采用供應商A供貨但不會采取援助措施，制造商2表示愿意繼續采用供應商A供貨并承諾援助總資金G來幫助供應商A能盡早完成生產，假設 δ為獲得援助后主供應商A的生產產能恢復系數，即此時主供應商A的實際交貨期變為tMM=(1-δ)t，制造商的實際交貨期變為，設當制造商援助資金為0 時，δ=0，最大調整系數為1/3[4]，制造商1和制造商2的各節點時間如圖4所示。

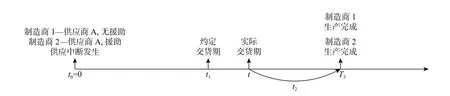
圖4 時間節點示意圖3Fig.4 Schematic 3 for time node

考慮制造商1、制造商2、供應商A之間勢均力敵，供應商A、制造商1、制造商2的期望利潤函數：

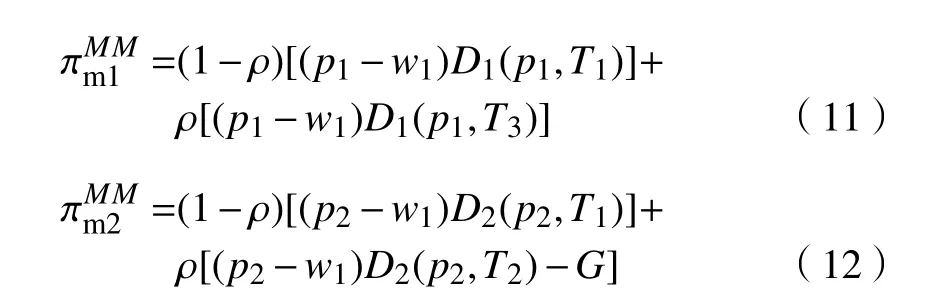
命題3存在納什均衡解使得供應商A、制造商1、制造商2各自收益最大。

證明

由式（13）可知，存在t*使得供應商A的期望利潤最大，存在p1MO*使得制造商1的期望利潤最大，存在p2MO*使得制造商2的期望利潤最大，令所以，

將tMM*代入p1MM*，p2MM*可得

2.4 制造商1采用供應商A供貨但并采取援助措施且制造商2采用備用供應商B供貨情形（策略4）

制造商1表示愿意繼續采用供應商A供貨并承諾援助總資金L1來幫助供應商A能盡早完成生產，制造商2表示將放棄供應商A并采用備用供應商B供應，假設ψ1為獲得援助后主供應商A的生產產能恢復系數，即此時主供應商A的實際交貨期變為tNO=(1-ψ1)t，制造商的實際交貨期變為，設，當制造商援助資金為0時，ψ1=0，最大調整系數為1/3[4]，制造商1和制造商2的各節點時間如圖5所示。

圖5 時間節點示意圖4Fig.5 Schematic 4 for time node

考慮制造商1、制造商2、供應商A之間勢均力敵，供應商A、制造商1、制造商2的期望利潤函數：

命題4存在納什均衡解使得供應商A、制造商1、制造商2各自收益最大。

證明方法如命題3所示，本文不作詳細證明，可得

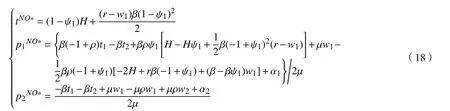
2.5 制造商1采用供應商A供貨并采取援助措施且制造商2采用供應商A供貨但不采取援助措施情形（策略5）

制造商1表示愿意繼續采用供應商A供貨并承諾援助總資金L2來幫助供應商A能盡早完成生產，制造商2表示將繼續使用供應商A供貨，假設ψ2為獲得援助后主供應商A的生產產能恢復系數，即此時主供應商A的實際交貨期變為tNM=(1-ψ2)t，制造商的實際交貨期變為T5=tNM+t2，ψ′(L2)＞0，設當制造商援助資金為0時，ψ2=0，最大調整系數為1/3[4]，制造商1和制造商2的各節點時間如圖6所示。

圖6 時間節點示意圖5Fig.6 Schematic 5 for time node

考慮制造商1、制造商2、供應商A之間勢均力敵，供應商A、制造商1、制造商2的期望利潤函數：

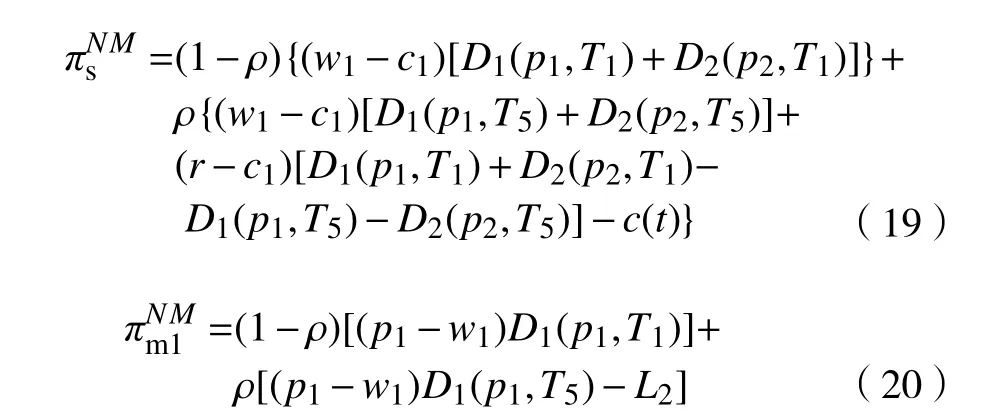
命題5存在納什均衡解使得供應商A、制造商1、制造商2各自收益最大。

證明方法如命題3所示，本文不作詳細證明，可得

2.6 制造商1采用供應商A供貨并采取援助措施且制造商2采用供應商A并采取援助措施情形（策略6）

圖7 時間節點示意圖6Fig.7 Schematic 6 for time node

考慮制造商1、制造商2、供應商A之間勢均力敵，供應商A、制造商1、制造商2的期望利潤函數：

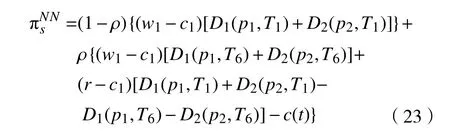
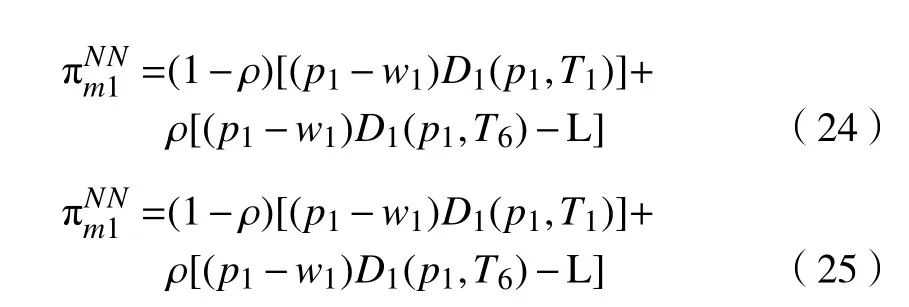
命題6存在納什均衡解使得供應商A、制造商1、制造商2各自收益最大。

證明方法如命題3所示，本文不作詳細證明，可得

2.7 模型分析

命題7當制造商1采用供應商A供貨但不采取援助措施時，制造商2不同策略下供應商A實際交貨時間滿足如下關系：

根據命題7可知，當制造商1采用供應商A供貨但不采取援助措施時，對比制造商2采用備用供應商B供貨和制造商2采用供應商A供貨但不采取援助措施的策略，采用供應商A供貨但不采取援助的策略的實際交貨時間更短，這是由于制造商2選擇供應商A供貨使得供應商A對未來盈利能力更為樂觀，此時供應商A愿意付出成本加快恢復供應鏈的正常運作。對比制造商2的3種策略，當制造商2愿意對供應商A進行援助時，只有當援助達到一定力度時，才能對供應鏈的恢復起到正向作用（表現為實際交貨時間的縮短），援助力度較小時反而會損害供應鏈的恢復，甚至制造商2采用供應商A供貨并采取援助措施策略的實際交貨時間大于制造商2采用備用供應商B。

命題8當制造商1采用供應商A供貨并采取援助措施時，制造商2不同策略下供應商A實際交貨時間滿足如下關系：

命題8、命題9的證明方法與命題7相同，本文不作具體證明。根據命題8可知，在不考慮備用供應商B供貨策略時，與命題7結論相似，當制造商1采取一定援助措施后，制造商2采取合適的援助措施能夠幫助供應商加快供應鏈中斷的恢復（表現為供應商A實際交貨時間的縮短），當援助力度較小時，制造商2的援助策略反而使得供應商A實際交貨時間延長。

命題9當制造商2采用3種不同策略時，制造商1不同策略下供應商A實際交貨時間滿足如下關系：

命題9表明，無論制造商2為了應對供應中斷采取何種策略，當制造商1采取合適的援助措施（援助系數大于閾值）都能夠加快供應鏈恢復。

3 算例分析

考慮云環境下2個制造商、2個供應商組成的時間敏感性供應鏈，供應商A存在供應中斷風險時制造商1和制造商2的策略選擇問題，參考相關文獻[4]，具體設置參數如表1所示。相關參數設置滿足文章基本假設，當w1=8時，w2＞8.1，結論恒成立。

表1 相關參數取值Tab.1 Values of relevant parameters

3.1 策略3～6中期望收益與恢復系數關系的數值算例分析

策略3中制造商2對供應商A采取援助措施，此時援助成本由制造商2決定，策略4，5中制造商1對供應商采取援助措施，此時援助成本由制造商1決定。策略6中制造商1、制造商2同時采取援助措施，此時援助成本由兩者共同決定。出于公平考慮，本文考慮制造商1和制造商2平均承擔援助成本。

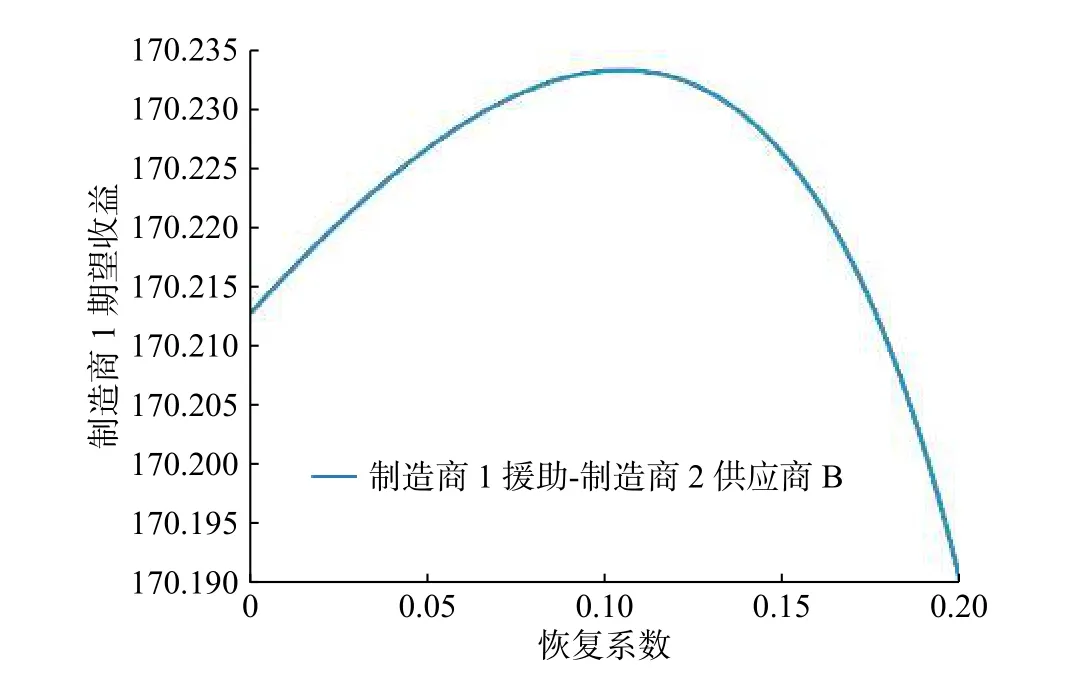
圖9 策略4中援助系數與制造商1期望收益的關系Fig. 9 Relationship between recovering coefficient and manufacturer 1 expected revenue in strategy 4

圖10 策略5中援助系數與制造商1期望收益關系Fig. 10 Relationship between recovering coefficient and manufacturer 1 expected revenue in strategy 5

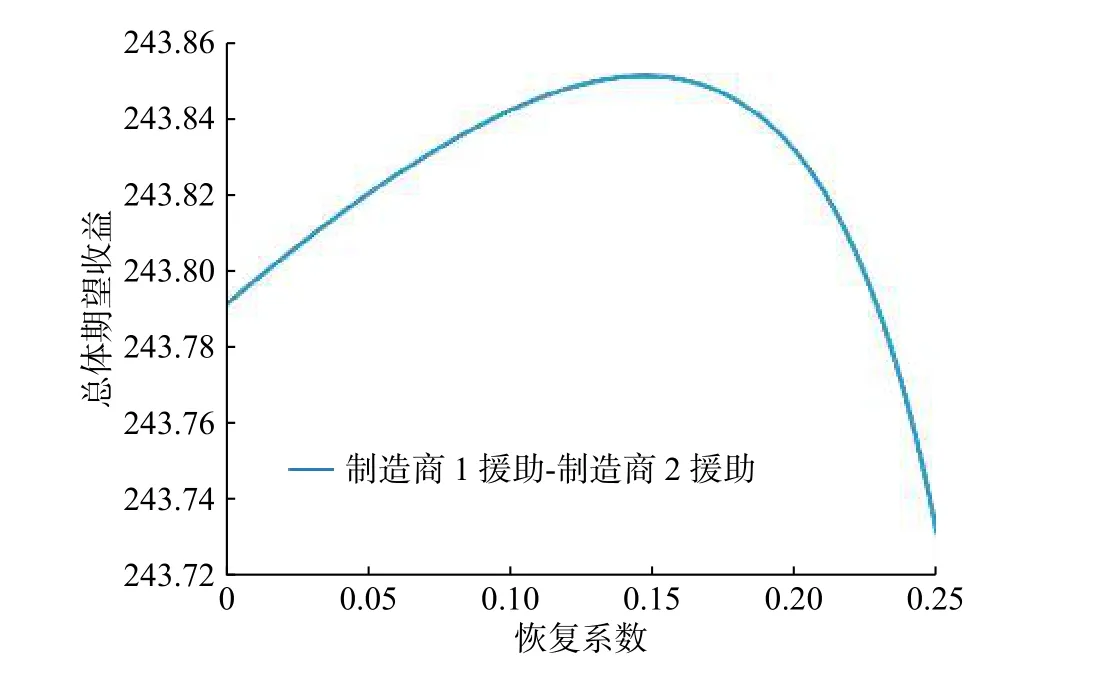
圖11 策略6中援助系數與總體期望收益的關系Fig. 11 Relationship between recovering coefficient and overall expected revenue in strategy 6

根據圖8～11可知，當中斷概率一定時（圖8～11中的中斷概率為0.1），制造商1的期望收益、制造商2的期望收益和總體期望收益均隨著恢復系數的增加而增大。恢復系數達到一定值后，制造商1的期望收益、制造商2的期望收益和總體期望收益均隨著恢復系數的增大而減小。這表明制造商1或制造商2單獨進行援助措施時，合適的援助措施能夠提高其自身的利潤。這是因為援助措施能夠引起零售價格和實際交貨時間的變動。當制造商1或制造商2采取合適的援助措施時，這種變動帶來的收益大于援助成本；當援助成本過高時，這種變動到來的收益低于援助成本，從而導致制造商1或制造商2利潤的下降。有關制造商1和制造商2均采取援助措施情形的分析與上文相似，此處不再作具體分析。

圖8 策略3中援助系數與制造商2期望收益關系Fig. 8 Relationship between recovering coefficient and manufacturer 2 expected revenue in strategy 3

將策略3、策略4、策略5和策略6在不同中斷概率下進行仿真，可知當0＜ρ＜1時，策略3中最優恢復系數為0.032，策略4中最優恢復系數為0.1，策略5中最優恢復系數為0.09，策略6中最優恢復系數為0.146。恢復系數精確至0.001，期望收益精確至0.000 1，最優恢復系數滿足任意中斷概率，算例分析中均使用最優恢復系數。

3.2 關于制造商生產完成時間數值算例分析

根據表2可知，當供應商A發生供應中斷時，制造商1和制造商2均采取援助措施時，供應商A的實際交貨時間最短。對比T3與T5可知，制造商1（單獨援助時）援助措施相對制造商2（單獨援助時）對供應商A供應恢復更為有效。因為，制造商1的產品市場需求量更大，采取的援助力度也會更大。

表2 最優恢復系數下實際交貨時間Tab.2 Actual delivery time under optimal assistance factor

3.3 關于制造商2的3種策略數值算例分析

3.3.1 制造商1不援助時制造商2的3種策略數值算例分析

根據表3可知，當制造商1采用供應商A供貨但不采取援助措施時，此時制造商2采取策略3（采用供應商A供貨并采取援助措施）獲得的收益最大，且隨著中斷概率的不斷增大，策略3相對其他2種策略的優勢更加明顯。

表3 制造商1不援助時制造商2的3種策略期望收益與中斷概率的關系Tab.3 Relationship between expected revenue and the probability of interruption in three strategies of manufacturer 2 when manufacturer 1 does not assist

3.3.2 制造商1援助時制造商2的3種策略數值算例分析

根據表4可知，當制造商1采用供應商A供貨并采取援助措施時，此時制造商2采取策略5（采用供應商A供貨但不采取援助措施）獲得的收益最大。對于策略6（采用供應商A供貨并采取援助措施），本文考慮制造商1和制造商2平均分攤援助成本，由于制造商1市場需求大于制造商2的市場需求。因此，制造商1以及供應商A會受益于制造商2的援助，但制造商2的收益反而會下降。對于策略4（備用供應商策略），由于備用供應商B批發價格昂貴，因此，制造商2選擇此策略期望收益遠低于另外2種策略，此時制造商采取策略5較為合適。

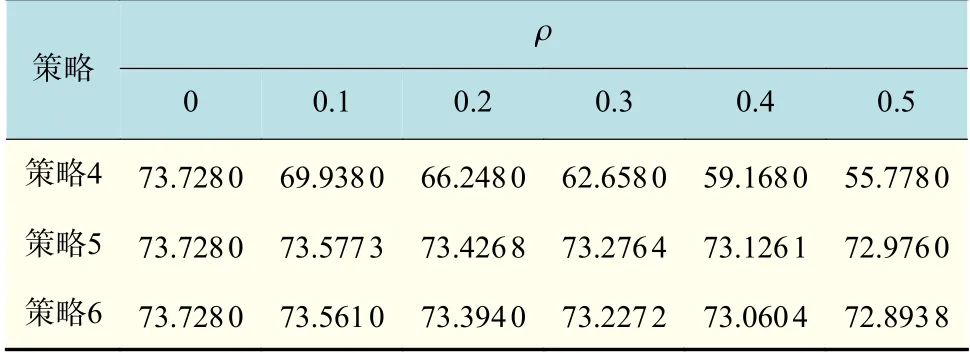
表4 制造商1援助時制造商2的3種策略期望收益與中斷概率的關系Tab.4 Relationship between expected revenue and the probability of interruption in three strategies of manufacturer 2 when manufacturer 1 assists

3.4 關于制造商1的2種策略數值算例分析

3.4.1 制造商2采用備用供應商B時制造商1的2種策略數值算例分析

根據圖12可知，當制造商2采用備用供應商B時，此時制造商1采取援助策略能夠獲得更多的收益，且中斷概率越大，制造商1援助策略獲得的超額收益越多。

圖12 策略1和策略4中制造商1的期望收益對比Fig. 12 Comparison of expected revenue of manufacturer 1 in strategy 1 and strategy 4

3.4.2 制造商2采用供應商A但不援助時制造商1的2種策略數值算例分析

根據圖13可知，當制造商2采用供應商A供貨但不采取援助措施時，此時制造商1采取援助策略能夠獲得更多的收益，且中斷概率越大，制造商1援助策略獲得的超額收益越多。

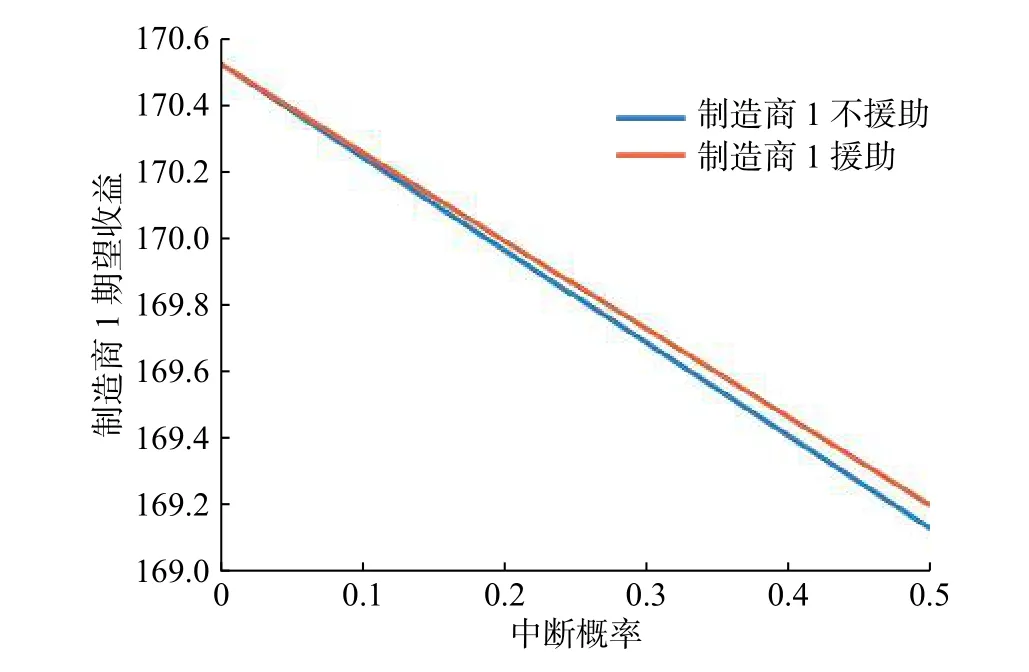
圖13 策略2和策略5中制造商1的期望收益對比Fig. 13 Comparison of expected revenue of manufacturer 1 in strategy 2 and strategy 5

3.4.3 制造商2采用供應商A并援助時制造商1的2種策略數值算例分析

根據圖14可知，制造商2選用供應商A并采取援助措施時，當供應中斷風險較低時，此時制造商1采取援助措施，相對不援助策略，制造商1能夠獲得更高的收益。但當供應中斷風險變大時，此時制造商采取援助措施反而會使得自身的收益下降。因此，制造商1應當充分評估供應中斷風險大小，及時采取不同的應對策略。

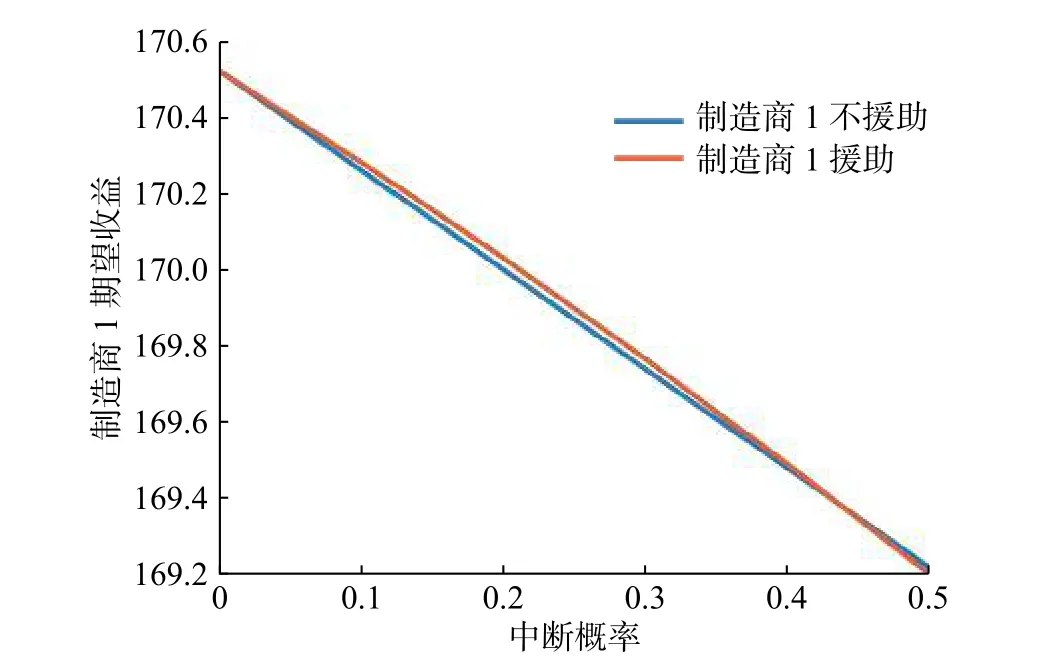
圖14 策略3和策略6中制造商1的期望收益對比Fig. 14 Comparison of expected revenue of manufacturer 1 in strategy 3 and strategy 6

4 結論與展望

對二階時間敏感性供應鏈進行研究，制造商1采用供應商A單源供應，制造商2采用供應商A供貨且擁有備用供應商B。當供應商A發生供應中斷時，制造商1可以采取2種應對策略（采用供應商A供貨但不采取援助措施，采用供應商A供貨并采取援助措施），制造商2可以采取3種應對策略（采用供應商B供貨，采用供應商A供貨但不采取援助措施，采用供應商A供貨并采取援助措施），建立制造商的期望利潤方程并通過算例對其進行分析，得到相關結論（制造商1和制造商2采取援助策略時的援助措施均為最優）：

a. 當供應商A發生中斷時，制造商1（或制造商2）單獨采取援助措施時，合適的援助成本能夠使制造商1（或制造商2）獲得更高的收益。

b. 當供應商A發生中斷時，制造商1和制造商2共同援助時，供應商A實際交貨時間最短。當制造商1的市場需求量相較于制造商2更大時，制造商1（單獨援助時）的最優援助措施相對制造商2（單獨援助時）對供應中斷恢復更為有效。

c. 當制造商1采用供應商A供貨但不采取援助措施時，制造商2采用供應商A供貨并采取援助措施時的期望收益相對其他策略更高；當制造商1采用供應商A供貨并采取援助措施時，制造商2采用供應商A供貨但不采取援助措施時的期望收益相對其他策略更高。

d. 當制造商2采用備用供應商B供貨或采用供應商A供貨但并不采取援助措施時，制造商1采用供應商A供貨并采取援助措施時的期望收益均高于其他策略；當制造商2采用供應商A供貨并采取援助措施時，制造商1策略選擇的優劣與中斷概率大小有關，當中斷概率較小時，制造商1選擇供應商A供貨并采取援助措施相對其他策略能夠獲得更高的收益，當中斷概率較大時，制造商選擇供應商A但不采取援助措施時相對其他策略能夠獲得更高的收益。

在今后的研究中，可以構建多制造商、多供應商的模型，對時間敏感性供應鏈中的供應中斷問題進行分析。