指向理性思維培育的活動設計

○于蓉

（作者單位：江蘇省揚州市育才小學東區校）

教學中，學生借助于某類事物的感性材料進行比較、歸納和初步抽象活動，并未能實現對事物間內在聯系的理性認識。隨著認識的不斷深入，需重視深層的理性思維活動，引導學生逐漸把握事物間的內在聯系，發展思維能力。數學活動，是小學生理性思維培育的重要外在形式。

指向理性思維培育的活動設計，應遵循數學活動設計的要求，進行學情調研、分析教學內容，開發活動資源，豐富活動材料，將活動目標轉化為問題，尋求符合兒童學習生活特點的情境，發揮數學學科對于培育學生理性思維的價值。

一、在核心處設計，凸顯概念本質，引發求真意識

高斯曾經指出：“在數學中重要的不是符號，而是概念。”教師應厘清知識點中核心的概念是什么，核心概念的本質屬性是什么，再通過設計活動讓學生感悟概念的豐富內涵。

【教學案例】在《認識垂線》這一課中會出現垂線、垂直線段、距離、垂足、互相垂直等較多知識點，教師在教學中一般是講完垂線，再講垂直線段、垂直，接著認識距離，熟記每段文字的內容，學生學得是百無聊賴。

【問題分析】一節課有較多知識點時，如果糾纏于每個知識點的具體內容，必然是咬文嚼字，遠離數學學科的育人目標。在認識線段時，學生已知兩點之間線段的長度是兩點間的距離，本節課是點到直線的距離，將問題進行轉化，在直線上找到一個點，這兩點間的線段長度就是點到直線的距離。這個點怎么找，就成為學生探索的目標。

【活動設計】

活動目標：點P到直線的距離是多少？

活動材料：在一個點上固定一把尺，尺可以繞固定點旋轉。

活動步驟：1.在點P外畫一條直線，在直線上點幾個點，并分別連接點P。

2.猜一猜：哪條線段最短？再驗證一下，它真的最短嗎？

3.想一想：這條線段是特殊而唯一的嗎？

4.說一說：點P到直線的距離是多少？說說你的理由。

活動中，學生用可以轉動的直尺量出每條線段的長度，并且在轉動中感受到垂直線段具有特殊性與唯一性，因此給予特別命名。在此基礎上再來認識垂足與距離，學生較容易接受和理解概念的內涵。

圍繞概念本質設計活動，需要教師將具體內容進行提升，成為指向本質概念的問題，從而發揮聚合作用，將零散的、孤立的知識點整合起來，促進學生的理解，引導學生求真。

二、在聯結處設計，豐富思考視角，引發求聯意識

數學知識是一個不可分割的整體，各個部分之間相互聯系。根據數學知識結構體系和學生已有的認知基礎設計數學活動，便于學生形成整體分析的視角，發揮這部分內容的育人價值。

【教學案例】在《分數乘分數》的教學中，教師常借助圖形幫助學生理解分數乘分數的計算規則。但一個班級的學情檢測數據表明，學生并未真正理解算理。

班里一共42名學生，有35人都不知道怎么寫，只有7人能畫出正確的結果。

問題二：你知道為什么分數乘分數時用分母相乘的積作分母嗎？

【問題分析】從“后測”可以看出，學生知道積的分母、分子與乘數的分母、分子的對應關系，但并未理解“為什么可以這樣做”。一是教材中都是真分數與真分數相乘的直觀模型，未涉及真分數與假分數相乘的直觀模型，學生對分數乘分數的理解具有局限性；二是學生還沒有將分數乘法與整數乘法的算理建立聯系。

【活動設計】在《分數乘分數》的練習課中進行整體設計。

活動一：計數單位相乘，會怎樣呢？

10×10 1×1 0.1×0.1 0.1×0.01

學生計算后交流，計數單位相乘，結果有可能變大，也有可能變小。

思考：分數單位相乘會怎樣呢？畫一畫，想一想。

活動二：算一算，比一比，有什么發現？

活動三：比一比，說一說可以怎樣比較？

a×b○a

整數乘整數、小數乘整數、分數乘整數的計算一直是合并與累加的過程，本質上仍是連加的計算。活動中引導學生發現分數乘分數就是先求出計數單位是多少，再求有多少個這樣的計數單位，使學生體悟到整數、小數、分數計算規則的一致性。活動三是讓學生進行分類思考，在比較中清晰地認識到整數、分數的計算規則具有一致性，但也具有各自的特點。

聯結處不僅是在數學內部尋找，還應在數學與其他學科、生活、學生的已有經驗中尋找，在求聯中感受數學的統一與和諧。

三、在易錯處設計，促進深度理解，引發求證意識

學生的易錯處是數學活動設計中需考慮的問題之一，教師應注意收集、分析原因，并根據學生年齡特點設計活動，有助于學生對學習內容有深入的理解，并在問題解決中有清晰的思路。

【教學案例】如圖，比較圖形①和圖形②的周長時，有近一半的學生認為圖形②的周長更長。即使在教師干預后，也有近30%的學生并不認可教師的觀點。

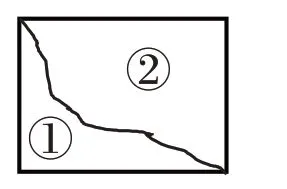
【問題分析】平面圖形的周長與面積是學生容易混淆的概念。周長是圍成的平面圖形一周邊線的長度；面積指圖形一周邊線圍成的平面的大小。兩者都和邊線有關，學生容易將面的大小與邊線的長短相混淆。

【活動設計】

活動目標：畫一條線，把長方形分成周長相等的兩部分。

活動材料：方格紙上有6個一樣的長方形。

活動一：把一個長方形分成兩個周長相等的圖形。

由于學生認知的局限性，畫出的圖形都是對稱的圖形。

活動二：把長方形分成兩個周長相等的圖形，還可以怎么分？畫一畫，再說一說。

由于有方格紙，學生可以通過數格子確定圖形的周長是多少。學生會看到圖形的長和寬沒有變，分割圖形的這條線段是公共邊，不管怎么畫，都不會影響兩個圖形周長的關系。

活動三：連接兩個相對的頂點，畫出的線把長方形分成的兩個圖形周長一樣嗎？說一說為什么？

活動中，學生會逐步打開自己的思維，不再局限于對稱的圖形周長相等，而是借助于格子數比較周長，在比較中優化比較的方法，在說一說中厘清思考的依據，進一步理解周長的內涵。

因數學的抽象性與兒童認知發展的漸進性、局限性存在沖突，學生在學習中出現錯誤是不可避免的。教師需關注學生在哪里出錯，分析錯誤的原因，進而設計活動觸及認知盲區，使學生逐步形成面對問題時審慎的態度和求證的意識。

四、在常規處設計，提升思維品質，引發創生意識

教師要善于在教學常規中挖掘提升學生理性思維的空間，通過尋求可以設計的活動元素，激活學生的思維。

【教學案例】教學《圓的周長》時，教師會花大量的時間讓學生測量、計算，獲得圓周率的近似值。課后訪談中卻發現，部分學生認為圓周率與3.14是相等的關系。學生不僅對圓周率沒有正確的認知，也未感受到圓周率讓眾多數學家與數學愛好者癡迷的魅力。

【問題分析】學生通過閱讀了解到圓周率與3.14有關系，通過測量感悟到圓周率是3多一些。但由于圓周率是無限不循環小數，學生只能看到一部分數字，并未理解圓周率表示的是周長與直徑的關系，是一個確定的數。由此，教學中讓學生感悟到圓周率是一個確定的數，則成為培育理性思維的一個契機。

【活動設計】

活動一：猜想——圓的周長與直徑可能有怎樣的關系？

學生形成猜想：圓周長與直徑的比值比2大，但比4小，是3多一些。

活動二：驗證——圓的周長與直徑的比值是3多一些嗎？

活動要求：

1.兩人合作，測量出所給不同圓的直徑和周長，填入表格。

2.用計算器計算出周長除以直徑的商（除不盡的得數保留兩位小數），并把結果填入表格。

3.根據算出的商寫下你的發現。

在學生測量的基礎上得出結論：不一樣的圓，它們的周長與直徑的比值都是3多一些。

疑問：比3多多少呢？測量是有誤差的，怎樣能讓數據更有說服力？

活動三：尋找——數學家用怎樣的方法確定圓周率是多少呢？

學生閱讀教師提供的資料，并觀看視頻，了解數學家研究圓周率的方法與歷程。

對于圓周率的探索，了解其意義只是目標之一，重要的是在探索圓周率的過程中感悟人類對未知的好奇與探索精神。活動中，引導學生在初步猜想的基礎上，通過測量確定猜想的準確性，再去尋求數學家的研究方法，感受數學家的嚴謹、求真與創新精神，從而激發學生對問題的探索與創生意識。

指向理性思維培育的活動設計，需要教師用心觀察學生的學習過程，找到學生學習中的障礙與盲區，將問題與學生經驗建立聯系；也需要教師深入理解數學內容本身，提煉出核心問題，在此基礎上盡可能地尋找符合兒童認知特點的活動背景，提供學習材料，達成學生在活動中積累理性思維經驗、提升數學素養的目標。