基于測距測角信息的DG-IEKF相對導航算法

劉梓軒，孫永榮，曾慶化，趙科東

(南京航空航天大學自動化學院導航研究中心，南京 210016)

0 引言

2015年，X-47B型無人機首次實現了自主空中加油。目前，在預對接前的會合編隊過程中，加油機與受油機間依賴于低延時戰術瞄準網絡技術數據鏈完成信息交互，通過傳播雙機的INS／GPS等導航信息實現高精度的相對位姿估計。在機間數據鏈中斷情況下，常規的相對導航策略無法滿足自主空中加油相對導航要求[1]，空中加油技術會合階段作為典型的合作目標相對導航問題實際上轉換為在沒有通信條件或者目標未配置主動傳感器的情況下的非合作目標相對定位問題[2]。對于中遠距離的無通信空中加油相對導航，通過態勢感知傳感器對未知環境進行目標識別與引導[3]，保證實時、高可靠、高精度的相對狀態估計是本文研究的重點。

在通信中斷的情況下，無人機常用的相對導航測量傳感器包括：以波達角度(Angle of Arrival，AOA)為量測的傳感器，如光電傳感器、紅外搜索跟蹤系統(Infrared Search and Track，IRST)等；以波達距離(Range of Arrival，ROA)為量測的傳感器，如激光測距儀等[4]；兼具AOA／ROA的傳感器，如激光雷達、合成孔徑雷達等[5]。選擇合適的態勢感知傳感器對未知環境進行探索是非常關鍵的。

對于非線性系統，擴展Kalman濾波(Extended Kalman Filter，EKF)是目前適用范圍最廣的非線性狀態估計濾波算法[6-7]。但在線性化過程中，EKF對非線性函數的Taylor級數進行了一階截斷處理，忽略了其高階項[8]。這種線性化處理在一些強非線性的情況下可能會使系統產生較大的誤差，使得濾波收斂速度緩慢[9]。為了進一步提高算法性能，迭代擴展Kalman濾波(Iterated Extended Kalman Filter，IEKF)得以發展[10-11]。IEKF可以看作是Gauss-Newton法在最大似然估計求解近似問題上的應用[12]，利用可充分信任的量測信息不斷迭代修正相對狀態，但在迭代初值或協方差誤差較大時，IEKF算法容易陷入局部極值點，明顯降低了濾波器的精度[13]。IEKF的迭代更新過程實際是對最優問題的求解，在最優問題求解中，每一步迭代都希望可以使目標函數值降低。信賴域狗腿(Dog-Leg，DG)算法作為一種Gauss-Newton算法與梯度下降算法的混合算法[14]，從迭代初值開始先劃定一個可以信賴的最大范圍，再以當前的工作點作為原點在預設的最大范圍內求解目標函數的最優解[15]，兼具了Gauss-Newton法與梯度下降法的優點。

本文在受油機與加油機間數據鏈中斷的情況下，通過綜合多個態勢感知傳感器提供的觀測信息，以雙機之間的直線距離、視線俯仰角與視線方位角作為傳感器輸出估計雙機間的相對狀態。同時，對于非線性系統的狀態估計算法，考慮到IEKF算法在狀態變量初始誤差較大時濾波收斂不理想的問題，本文借鑒了DG算法的優化思想，將信賴域求解最優解過程引入IEKF算法中的迭代更新過程，提出了一種DG-IEKF(Dog-Leg Iterated Extended Kalman Filter)算法。最后，通過與EKF、IEKF算法的對比分析驗證了本文算法的有效性。

1 測距測角信息下的相對導航系統模型

1.1 非合作目標CA模型

在地心地固坐標系下，定義受油機絕對位置坐標向量為Xf＝[xfyfzf]， 加油機絕對位置坐標向量為Xl＝[xlylzl]， 狀態變量為x＝[ΔXΔX′ ΔX″]T。其中，ΔX＝Xl－Xf為受油機與加油機之間的相對位置， ΔX′和ΔX″分別為受油機與加油機之間的相對速度和相對加速度。在雙機加油過程中，加油機一般在指定空域中進行勻速直線運動，而受油機一般以高于加油機的速度接近加油機，雙機速度都較為穩定且機動較小。因此，在相對導航目標為非合作目標的情況下，選取勻加速(Constant Acceleration，CA)模型作為相對運動模型。離散化狀態方程為

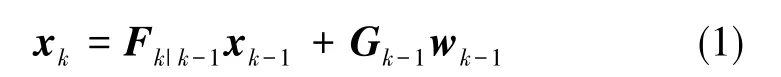
式(1)中，Fk｜k－1和Gk－1分別為狀態轉移矩陣和系統噪聲矩陣，wk－1為3×1維的相互獨立的零均值Gauss白噪聲向量。其中，Fk｜k－1和Gk－1滿足

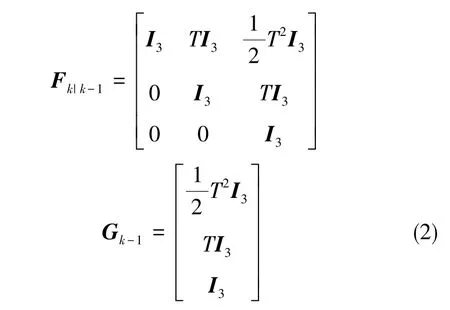
式(2)中，I3為三階單位矩陣，T為采樣間隔。

1.2 測距測角信息下的量測方程

根據非合作目標定位原理，可以得到相對空間幾何模型。本文相對導航的目的就是利用受油機上配置的主被動傳感器測得與目標之間的距離與角度信息[ραβ]，計算出受油機與加油機之間的相對位置ΔX＝Xl－Xf＝[xl－xfyl－yfzlzf]T。 如圖1所示，可得地心地固坐標系下受油機與加油機之間的空間幾何關系

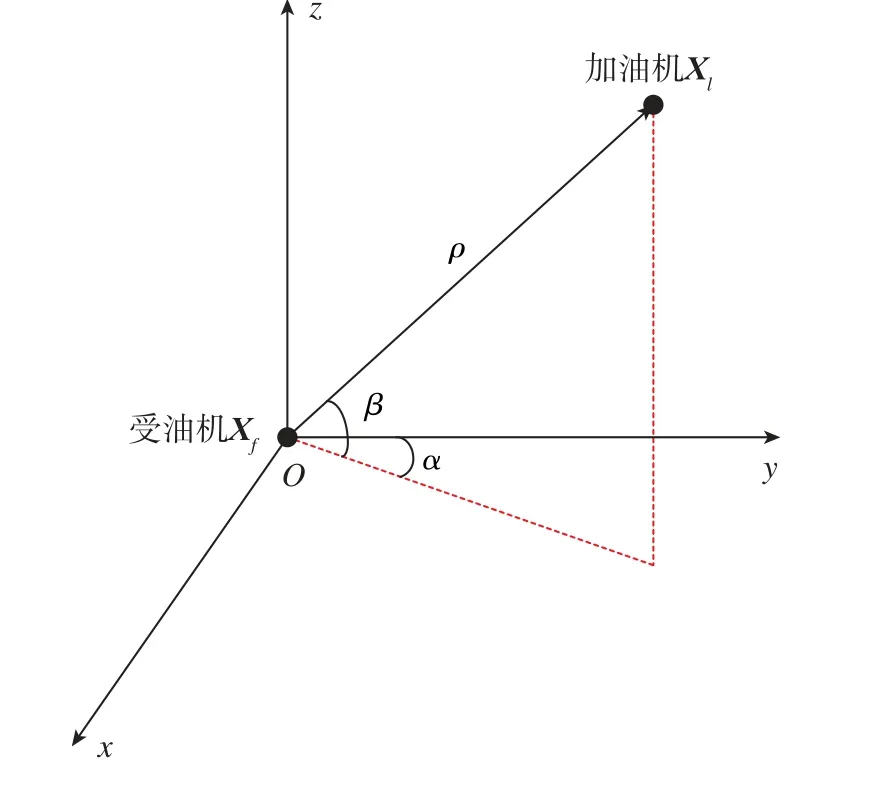
圖1 相對導航空間幾何關系示意圖Fig.1 Schematic diagram of relative navigation geometry

由式(3)可以建立在測距測角信息下的相對導航系統量測方程

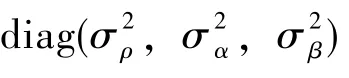
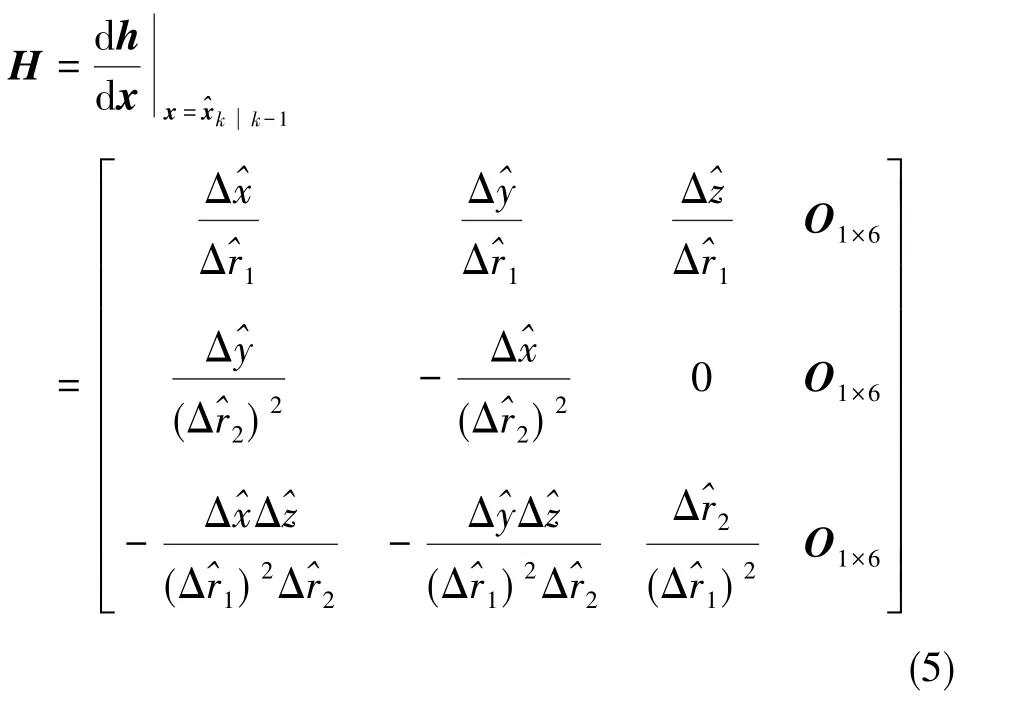
2 基于信賴域狗腿算法優化的IEKF算法

2.1 IEKF算法與Gauss-Newton算法的一致性分析

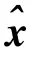
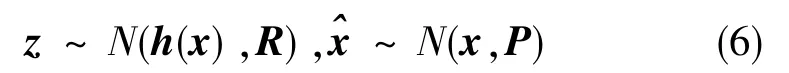
式(6)中，P為狀態變量協方差陣。將量測與狀態變量估計值組合構造一個偽觀測量，并對量測矩陣也進行相應的構造

根據式(7)可得

用最大似然函數L(x)表示Z關于狀態變量x的概率密度，有

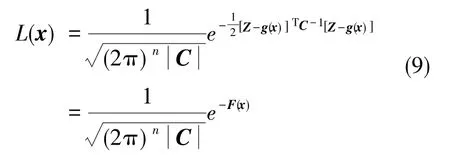
定義

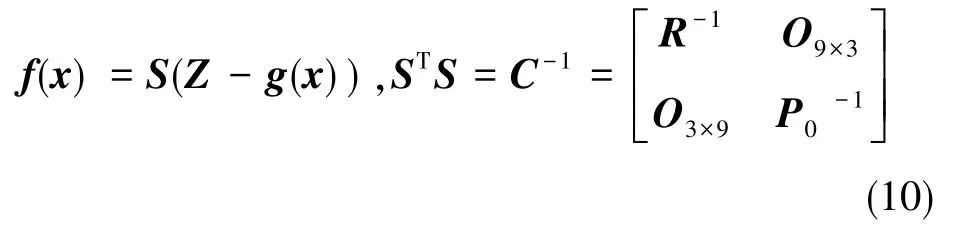
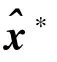
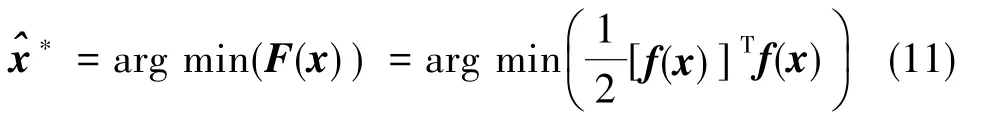
由式(11)可得，IEKF迭代更新的最大似然目標函數與非線性最小二乘問題的目標函數是等價的。至此，將IEKF的量測更新過程轉化為求解非線性最小二乘問題。

Gauss-Newton算法對式(11)的解為

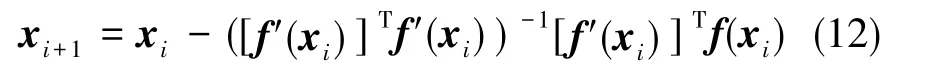
對式(12)進行整理，可得

式(13)中，根據矩陣逆的性質可得

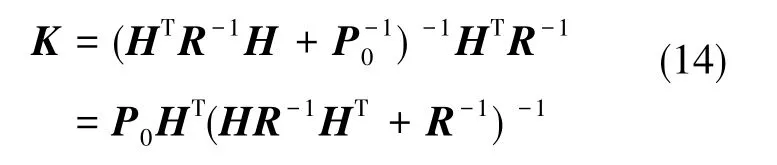
式(13)與IEKF狀態遞推公式完全一致，IEKF算法可以看作Gauss-Newton算法在最大似然估計求解近似問題上的應用。而Gauss-Newton算法只有在滿足一定局部性條件的情況下才能穩定收斂，這也解釋了IEKF算法在初始誤差較大情況下可能失效的原因。因此，作為一種Gauss-Newton算法的改進顯式信賴域算法，將狗腿算法引入IEKF算法，可以有效優化IEKF算法中的狀態變量迭代更新過程，增強算法的收斂性與穩定性。

2.2 信賴域狗腿算法

信賴域算法是一種最優化方法，能夠保證目標函數最優化總體收斂。本文的信賴域狗腿算法為梯度下降算法與Gauss-Newton算法的混合算法，在求解函數極小值的最優化算法中，每一次迭代都要求目標函數是下降的，從初始點開始先劃定一個可以信賴的最大位移量，在預設的最大范圍內求解目標函數的最優解，并根據實際的下降量自適應地劃定信賴域范圍。信賴域狗腿算法的基本思想是：通過比較梯度下降算法的迭代步長、Gauss-Newton算法的迭代步長與劃定的信賴域范圍來計算迭代增量。在迭代初值誤差較大時，通過接近梯度下降算法的迭代步長快速下降，有助于快速收斂；在接近最優值時，通過接近Gauss-Newton算法的迭代步長逼近最優值，避免了梯度震蕩。由此，減少了函數陷入局部極小值的情況。

假設非線性最小二乘的目標函數為

定義

根據式(12)，可得Gauss-Newton算法的迭代步長為

根據梯度下降算法的原理，迭代下降方向為

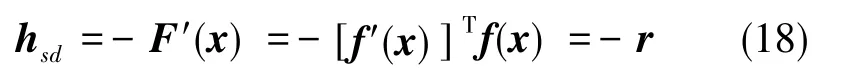
選取合適的步進長度，從而得到最大程度的迭代下降。

假設f(x+τhsd)≈f(x)+τ[f′(x)]Thsd， 代入式(15)可得

結合式(18)與式(20)，可得梯度下降算法的迭代步長為

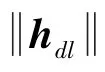
因此，Δ、τhsd、hgn與hdl的關系示意圖如圖2所示，通過比較Δ、τhsd、hgn來確定DG算法最終迭代步長hdl

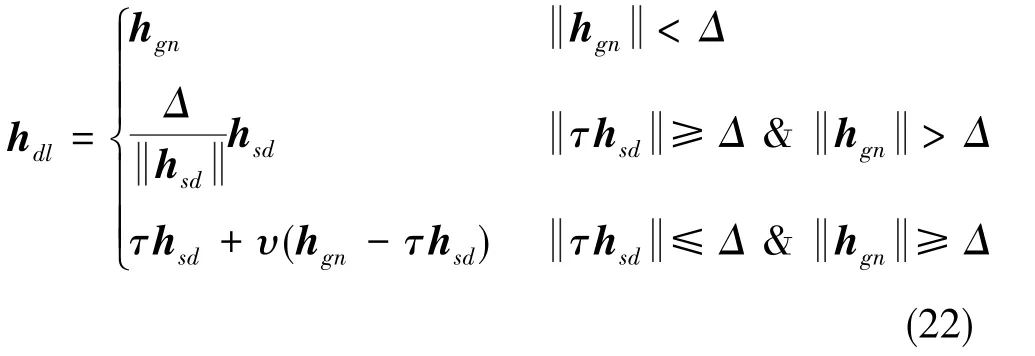
在計算出DG算法迭代步長后，還需衡量近似模型對于真實模型的準確性，使用預測下降量與實際下降量的比值進行評判，并對信賴域Δ進行自適應調整。

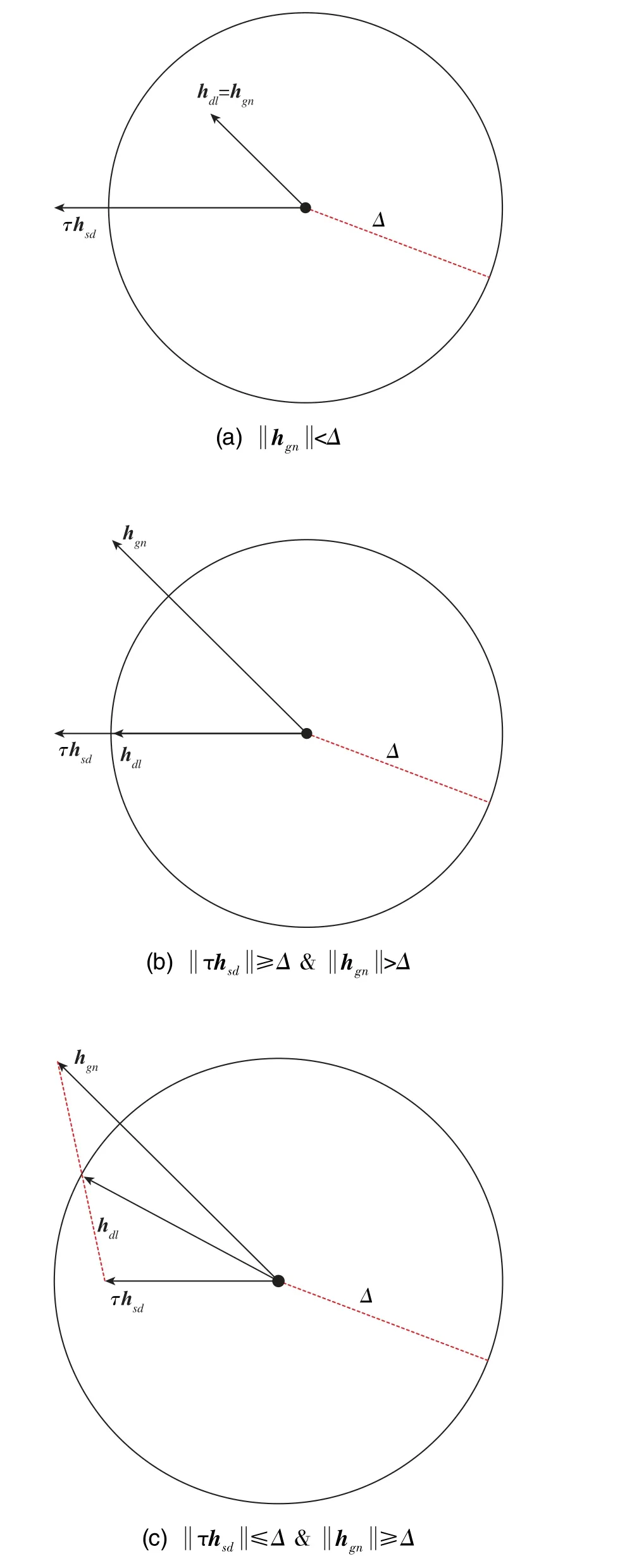
圖2 迭代步長關系示意圖Fig.2 Diagram of iteration step relationship

近似模型的下降量為

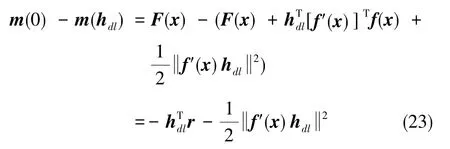
定義比值

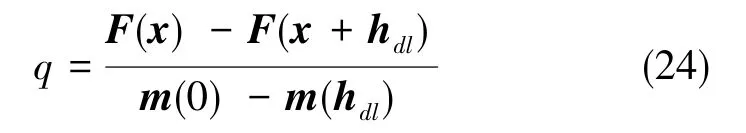
式(24)中，阻尼因子q用于衡量二次模型與目標函數的逼近程度。

根據所得到的q來進行DG算法的迭代更新，并自適應調整下次迭代的信賴域半徑Δ：

1)當q≤0時：xi+1＝xi

當前迭代步長不合理，縮小信賴域半徑，使得Δi+1＝Δi／2， 重新計算試探當前迭代步長。

2)當q＞0時：xi+1＝xi+hdl

若q＞0.75，二階近似效果較好，可適當擴大信賴域半徑，使得Δi+1＝2Δi。

若0.25≤q≤0.75，保持信賴域半徑不變，使得Δi+1＝Δi。

若q＜0.25，二階近似效果較差，可適當縮小信賴域半徑，使得Δi+1＝Δi／2。

2.3 DG-IEKF狀態更新方程與協方差更新方程的推導

通過借鑒DG算法的思路，并分析IEKF算法狀態變量的迭代更新過程，推導DG-IEKF算法的狀態更新方程與協方差更新方程。

結合式(12)與式(16)，可得

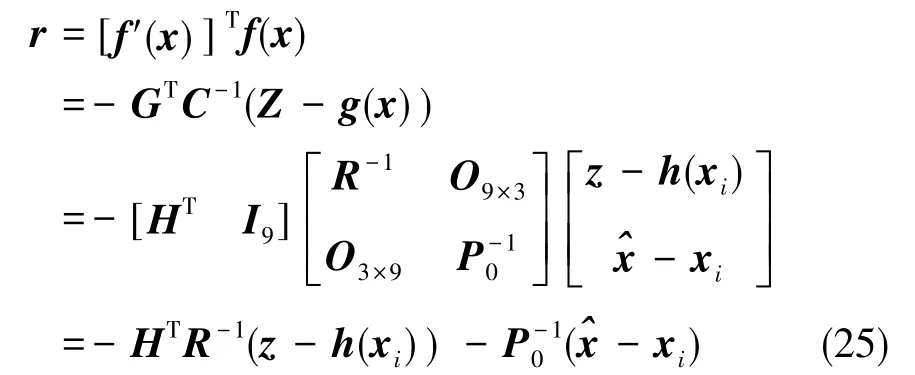
結合式(17)與式(25)，可得

結合式(21)與式(25)，可得

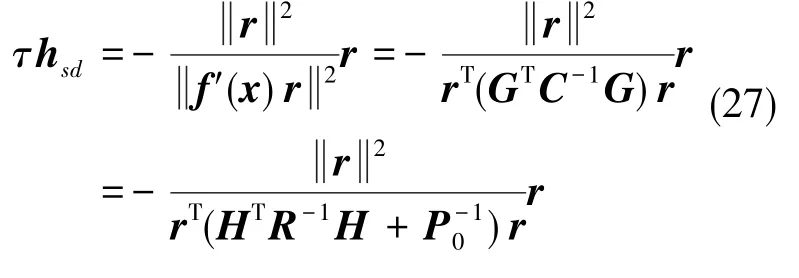
根據式(22)，可確定DG-IEKF算法的迭代步長hdl。計算阻尼因子q來衡量二次模型的近似程度，來判斷步長的有效性

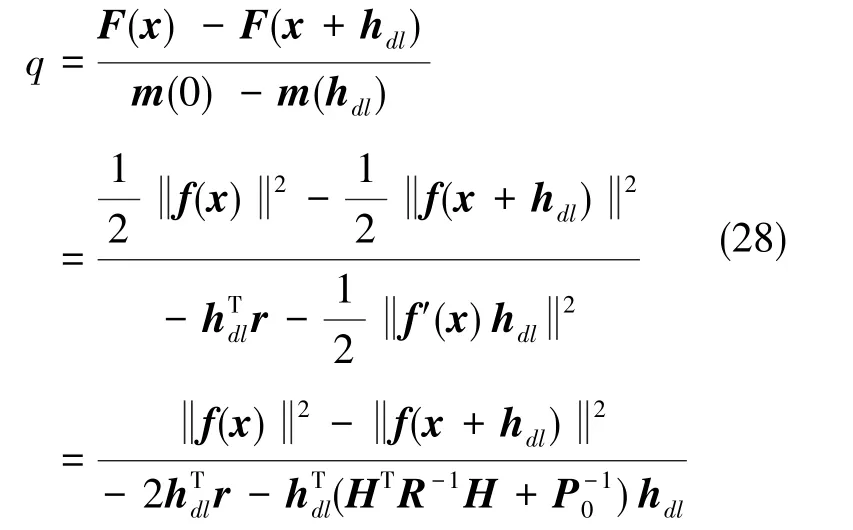
結合式(22)與式(28)，可得DG-IEKF算法的狀態更新方程

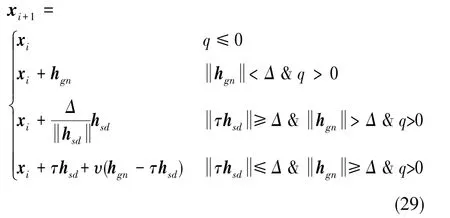
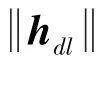
根據式(15)，令F′(x)＝0， 求取極值點，可得

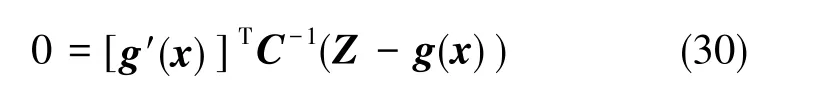
由線性一階近似可得

將式(31)代入式(30)，可得

整理可得

由式(9)可知：Z－g(x)～N(O12×1，C)， 可得DG-IEKF算法的協方差陣更新方程

2.4 DG-IEKF算法流程

根據上文推導的DG-IEKF算法的狀態更新方程與協方差更新方程，可得DG-IEKF算法流程如圖3所示。其中，迭代終止門限值μ、η和最大迭代次數γ依賴于實際經驗設定。

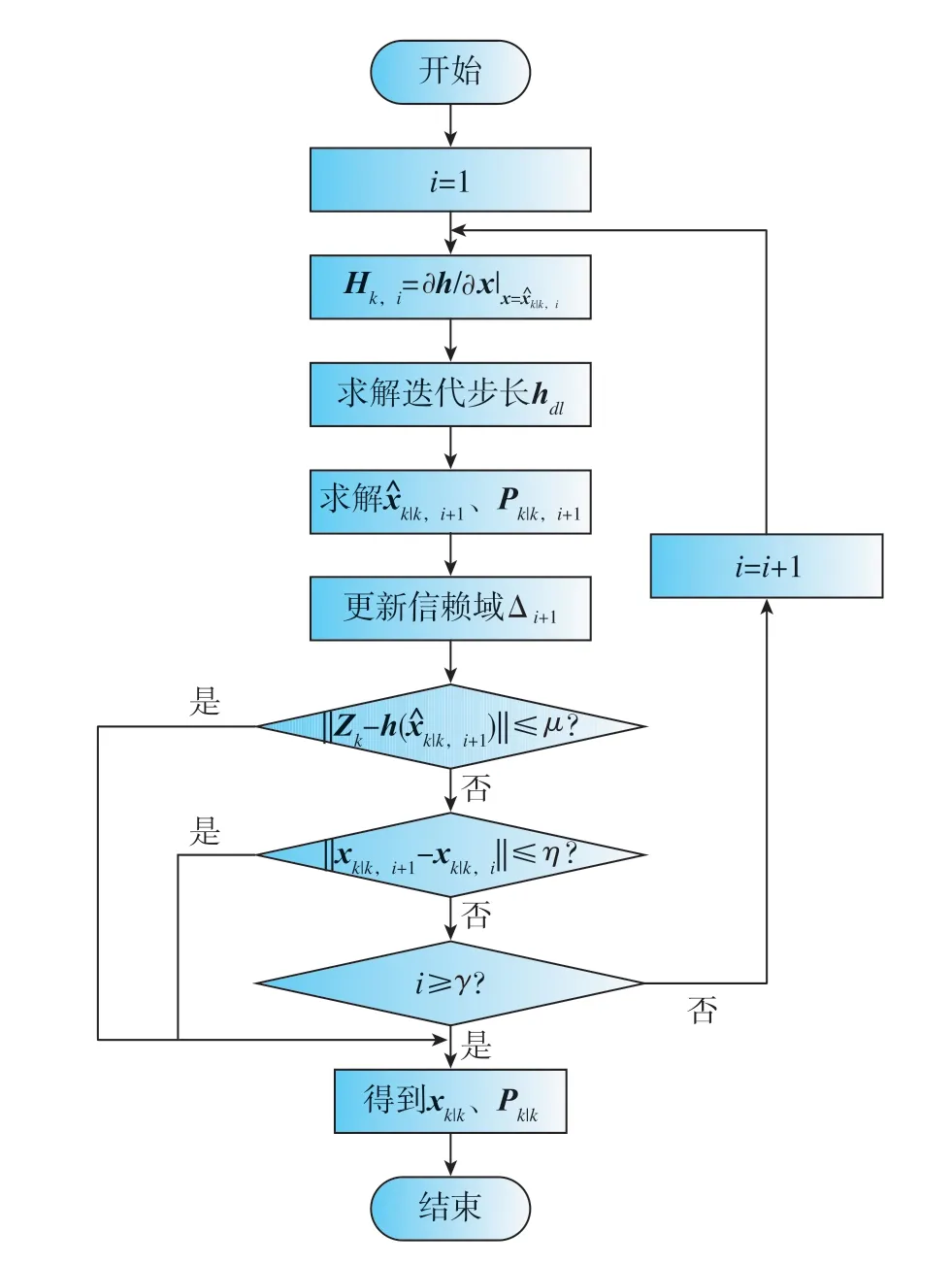
圖3 DG-IEKF算法流程圖Fig.3 Flowchart of DG-IEKF algorithm

3 實驗與分析

為了驗證DG-IEKF算法的有效性，本文采用Monte-Carlo方法開展仿真驗證，共進行了100次仿真。與EKF算法、IEKF算法進行了比較，通過應用平均絕對誤差(Mean Absolute Error，MAE)和均方根誤差(Root Mean Square Error，RMSE)來評價算法精度。

3.1 仿真條件

設置仿真時間為300s，設置測距測角傳感器精度[σρσασβ]T為[30m 2mrad 2mrad]T，傳感器量測更新頻率為2Hz，采樣頻率為2Hz；受油機初始位置為[118° 31.8649° 8000m]T，機體系下初始速度為[0m／s 50m／s 0m／s]T，初始加速度 為[0m／s20m／s20m／s2]T， 初 始 姿 態 為[0° 0° 0°]T；加油機初始位置為[118.0225°31.8640° 7795.35m]T，機體系下初始速度為[0m／s 50m／s 0m／s]T，初始加速度為[0m／s20m／s20m／s2]T，初始姿態為[0° 0° 0°]T。加油機向東勻速直線飛行，受油機在機體系下的飛行軌跡參數如表1所示。地心地固坐標系下，雙機相對運動軌跡如圖4所示。

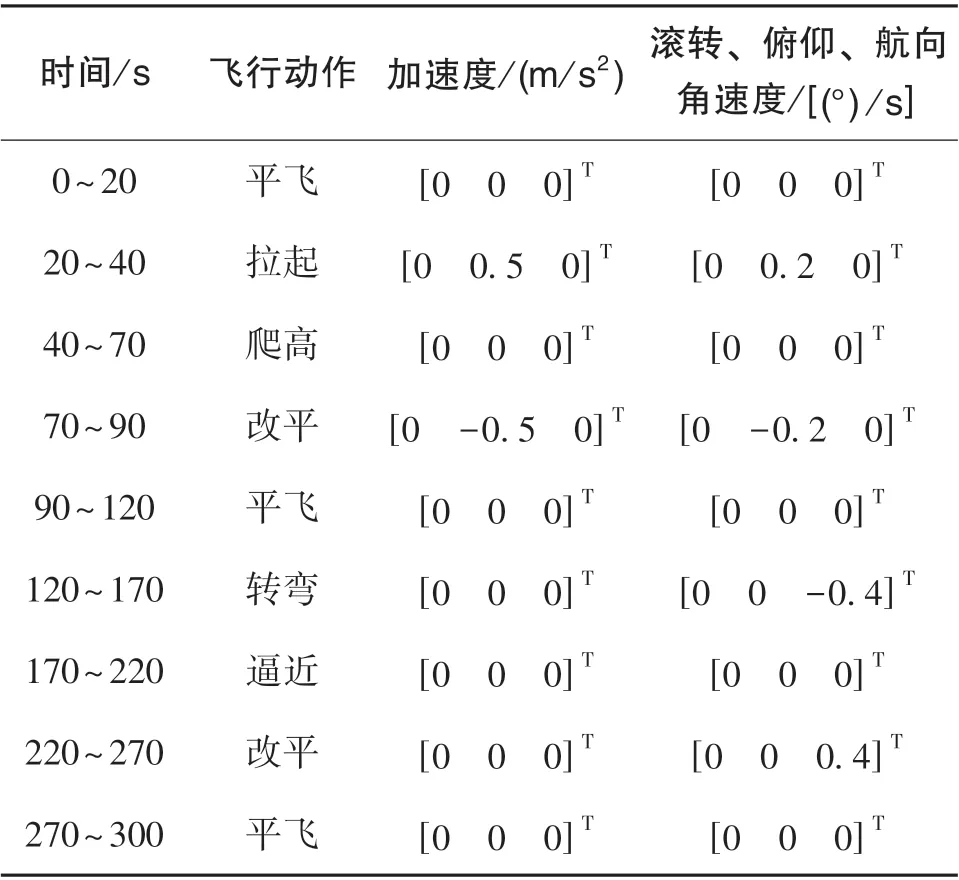
表1 受油機飛行軌跡參數Table 1 Parameters of oilreceiver flight trajectory

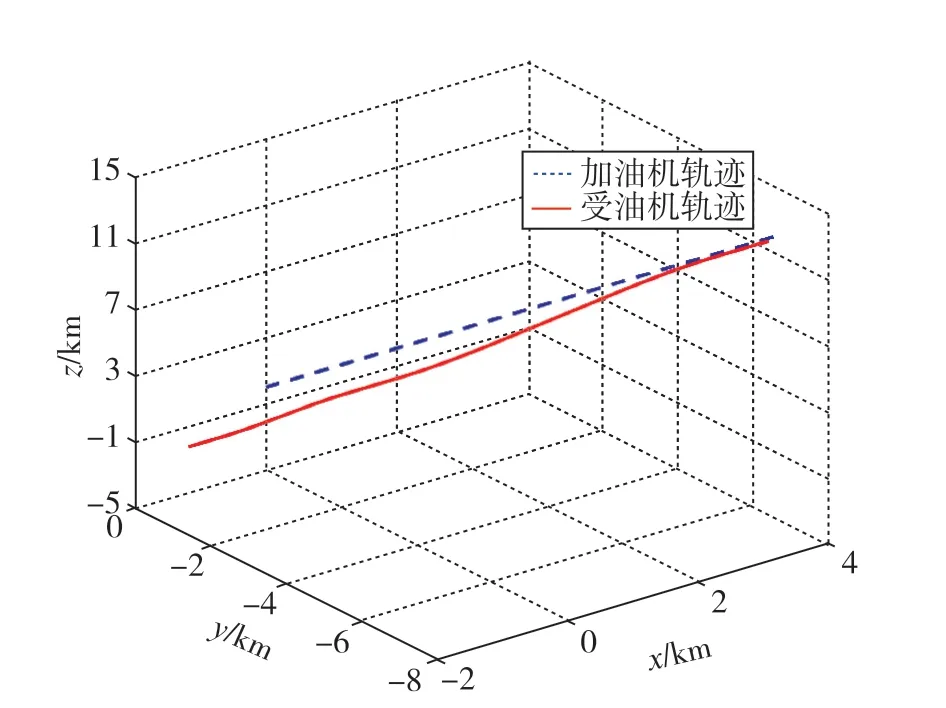
圖4 雙機相對運動軌跡Fig.4 Diagram of two aircrafts'relative motion trajectory

3.2 仿真結果分析

采用Monte-Carlo方法統計這100次的仿真結果。通過對每次采樣的100組數據取平均值繪制曲線，相對位置誤差曲線如圖5(a)所示，相對位置RMSE曲線如圖5(b)所示；相對速度誤差曲線如圖6(a)所示，相對速度RMSE曲線如圖6(b)所示。

圖5 相對位置誤差與相對位置RMSE對比示意圖Fig.5 Comparison diagram of relative position error and relative position RMSE

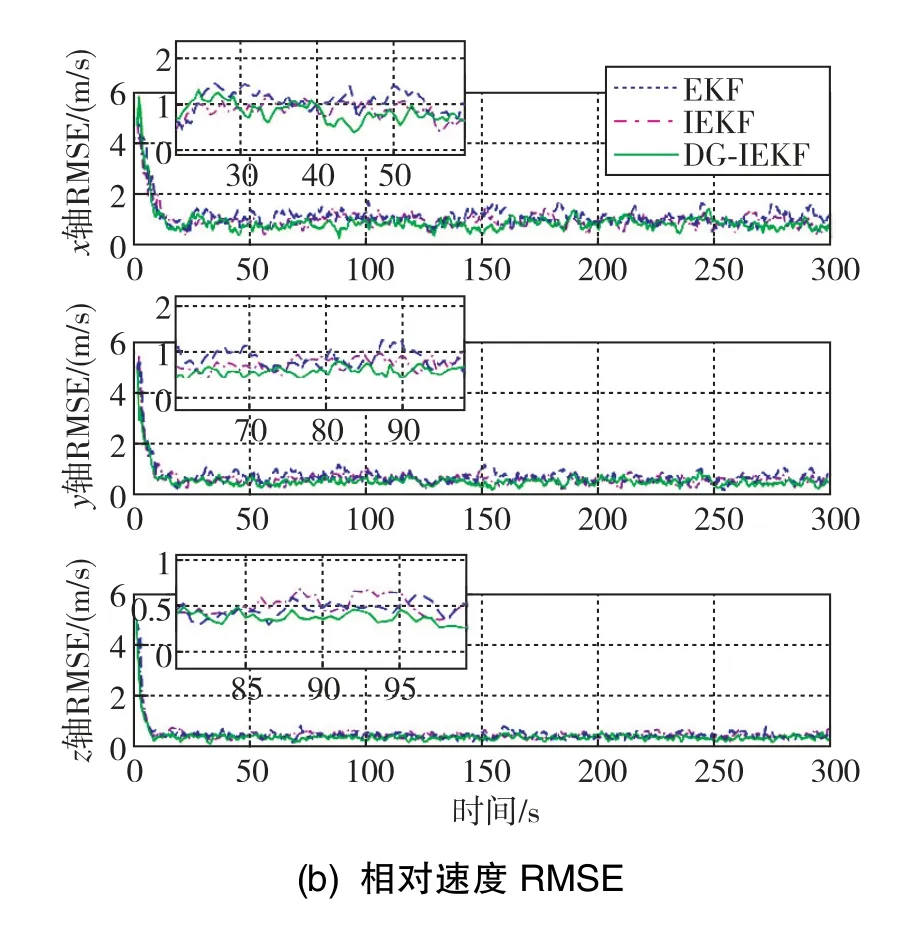
圖6 相對速度誤差與相對速度RMSE對比示意圖Fig.6 Comparison diagram of relative speed error and relative speed RMSE

由圖5(a)、圖6(a)可知，在相對導航信息初始對準存在較大誤差時，本文的DG-IEKF算法能夠更有效、更準確地逼近相對位置真實值，具有更快的收斂速度。在受油機軌跡發生較大變化的50s～100s內，EKF算法出現了數次較大的毛刺，而DG-IEKF算法則相對更加平穩，避免了陷入局部極值點的情況。圖5(b)、圖6(b)分別為相對位置與相對速度的RMSE對比曲線，代表DG-IEKF算法的綠色曲線在全仿真階段的誤差總體上低于EKF算法與IEKF算法，對比可知DG-IEKF算法具有較好的穩定性。綜合圖5、圖6可以看出，在相對位置與相對速度方面，DG-IEKF算法要優于EKF與IEKF算法。

表2為三種算法對相對導航狀態的誤差統計，分別計算了三種算法在綜合MAE與綜合RMSE下x軸、y軸與z軸的相對狀態精度。綜合RMSE基于L2范數計算，對偏差的敏感性更高。與EKF算法相比，DG-IEKF算法在x軸、y軸、z軸上的相對位置MAE精度分別提高了21.17%、20.42%、18.42%，相對位置RMSE精度分別提高了37.18%、36.05%、33.42%；相對速度MAE精度分別提高了12.55%、11.76%、11.33%，相對速度RMSE精度分別提高了20.57%、18.84%、18.19%。

表2 MAE與RMSE誤差統計對比Table 2 Comparison of MAE and RMSE error statistics

4 結論

針對相對導航數據鏈中斷的情況，本文提出了一種在測距測角信息下基于狗腿算法優化的DGIEKF狀態估計算法，通過態勢感知傳感器輔助雙機進行相對導航，接續常規相對導航策略完成相對導航任務。該算法借鑒信賴域優化思想改進IEKF中狀態迭代更新過程，以提高相對導航濾波器的精度與可靠性。仿真實驗結果表明，本文的DG-IEKF算法與現廣泛使用的非線性濾波EKF算法相比，在RMSE方面，相對位置綜合精度提高了35.55%，相對速度綜合精度提高了19.20%，能夠在常規導航策略失效時穩定可靠地完成相對導航任務。