考慮三源不確定性的Wiener過程航空發動機剩余使用壽命預測

趙廣社，趙春濤

(1.西安工程大學 電子信息學院，陜西 西安 710048；2.西安交通大學 電子與信息學部，陜西 西安 710049)

0 引 言

航空發動機作為飛機的核心部件，其可靠性和安全性至關重要。但是，航空發動機不僅結構復雜，而且運行環境復雜多變，因而航空發動機的故障具有易發生、模式多、多故障模式同時存在等特點。預測與健康管理(prognostics and health management, PHM)是一種降低故障率、保證飛行安全的有效方法[1]，其中RUL預測是PHM中的關鍵技術之一。RUL可以定義為系統或部件可繼續正常使用的時間長度[2]，即當前時刻與失效時刻之間的時間間隔。RUL預測通過分析監測數據或建立合適的性能退化模型對系統或部件的RUL進行預測。

現有RUL預測方法分為3類：基于經驗的預測方法[3]、數據驅動的預測方法[4]和基于物理失效模型的預測方法[5]。基于經驗的預測方法易理解、易實現[6]，但其預測精度有限，并且依賴大量歷史數據。基于物理失效模型的預測方法具有預測精度高的優點[7]，但需要構建準確的物理失效模型，對航空發動機這種復雜系統來說極難實現。基于數據驅動的預測方法通過挖掘退化數據內在的信息[8]，以表現系統自身變化及工作環境影響導致的系統失效，它避免了復雜的物理失效模型的構建過程，且準確率較高。因此，本文主要研究的是基于數據驅動的航空發動機RUL預測。

目前，基于數據驅動的RUL預測是研究的熱門，并且擁有大量成熟的退化模型，如隨機系數模型[9]、隨機過程模型[10]和濾波模型[11]等。在基于隨機過程的退化模型中，常常采用Wiener過程退化模型。WANG提出了基于EM算法的退化模型未知參數估計方法[12]。劉君強等通過實驗證明了航空發動機的退化過程可以劃分為幾個不同的退化階段[13]。黃亮等建立了多階段Wiener過程性能退化模型，并實現航空發動機的RUL預測[14]。然而，對于發動機這種復雜系統，在退化過程中還普遍存在三源不確定性，即時變不確定性[15]、個體差異不確定性[16]、測量不確定性[17]。現有關于三源不確定性的文獻較少。ZHENG等首次將三源不確定性引入到線性Wiener過程退化模型中[18]，然而，該文獻并沒有考慮退化過程中的非線性性，WANG等同時考慮了非線性性和三源不確定性，并且證明了考慮三源不確定性可以有效提高預測精度[19]。DONG等利用粒子濾波實現了對鋰電池的RUL預測[20]。王璽等同時考慮三源不確定性和非線性實現對航空發動機排氣溫度裕度的預測[21]。然而，上述考慮三源不確定性的研究中，在考慮測量不確定性時都假設測量誤差服從正態分布，但正態分布不適合用來描述極端值(測量誤差較大)出現概率較大的情況。

對于目前航空發動機RUL預測存在的問題，本文建立了考慮三源不確定性的非線性Wiener過程性能退化模型，將三源不確定性引入退化模型并且假設測量誤差服從Logistic分布。提出一種基于最大熵無跡粒子濾波和條件期望最大化算法的參數估計方法。最后，采用大型渦輪風扇發動機數據集C-MAPSS進行仿真實驗,驗證本文方法的有效性。

1 三源不確定性的剩余壽命預測方法

1.1 模型描述

性能退化過程{X(t),t>0}被標準Brown運動B(t)驅動，那么一般的非線性Wiener過程可表示為

(1)

式中：λ為漂移系數；σB為擴散系數；ρ(τ，θ)為時間t的非線性函數；θ為未知參數；x0為初始退化狀態，x0=0。如果ρ(τ，θ)=ρ那么該式就變成線性退化模型，可見該退化模型不失一般性。

從實際角度出發，個體差異不確定性是指同型號同批次的航空發動機，受到不同的外部工作環境和內部因素的影響，不同個體的性能退化過程也是存在差異的。因此，在退化模型中引入個體差異不確定性是必要的。根據文獻[22],假設漂移系數λ為隨機參數，來表現個體間差異的不確定性，建立參數λ的更新機制為

λn=λn-1+γ

(2)

受到傳感器精度、外部運行環境噪聲等因素的影響，測量誤差是不可避免的。因此，有必要在建立退化模型時引入測量誤差不確定性。為了表示這種測量誤差，令測量過程{Y(t),t>0}為

Y(t)=X(t)+ε

(3)

式中：ε為測量誤差。為了更好地擬合測量誤差極端值出現概率較大情況下的退化過程，假設ε服從Logistic分布。

Logistic分布與正態分布形狀相似，其概率密度函數為

(4)

式中：v為位置參數；s為尺度參數。由式(4)可以算出Logistic分布的超額峰度系數為1.2。通過超額峰度系數可知Logistic分布具有尖峰、厚尾的特征，因此Logistic分布比正態分布適合描述測量誤差極端值出現概率較大的情況，Logistic分布也就常被用來在統計推斷中增加推斷的可靠性。同時，假設ε、λ和B(t)是相互獨立的。

可以得出性能退化數據X(x1,x2,…,xn)的考慮三源不確定性的非線性Wiener過程性能退化模型的狀態空間模型為

(5)

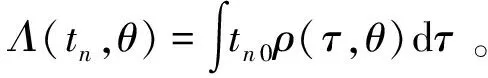
至此，已經在非線性退化模型中引入了三源不確定性。將性能退化狀態xn和隨機參數λn作為“隱含”狀態，進一步整理式(5)可得退化模型的狀態空間模型：

(6)

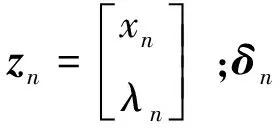
1.2 關鍵檢測參數選取

實際上，每一個監測參數對退化過程造成的影響不同，為了進行準確的RUL預測，要篩選出對退化過程影響大的監測參數[23]。航空發動機的退化過程是必然發生且不可逆轉的，對發動機退化過程貢獻大的參數應具有單調性的特點。文獻[24-25]采用定性分析監測參數的單調性來篩選關鍵參數，但該方法只是定性分析，并沒有對參數的變化趨勢進行量化，不能區分不同參數的變化程度。因此，采用Spearman系數計算各個監測參數的單調趨勢，可表示為

(7)

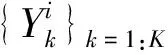
由式(7)可以看出，Spearman系數的取值范圍為[-1,1]。當參數值是常數或者隨時間變化隨機變化時，那么Spearman系數值為0；參數值隨時間變化增加時，Spearman系數值大于0，參數值隨時間變化的單調增加趨勢越，Spearman系數值越接近于1，當參數值隨時間完全單調增加時，Spearman系數值為1 ；參數值隨時間變化的單調減少趨勢越明顯，Spearman系數值越接近于-1，當參數值隨時間完全單調減少時，Spearman系數值為-1。

基于上述分析，為了使選取的監測參數擁有明顯的單調性同時能夠盡量全面地表現航空發動機的退化過程，選取趨勢值超過閾值0.5的參數進行后續的航空發動機RUL預測。

1.3 最大熵無跡粒子濾波算法

用監測數據Y0:n估計的zn的期望和協方差分別為

(8)

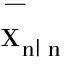
一步前向的期望和方差為

(9)

根據上述假設，可以用最大熵無跡粒子濾波算法聯合估計性能退化正態和隨機參數組成的zn。

根據式(6)，基于監測數據Y0:n，RUL的概率密度函數可表示為

(10)

式中：

2 實例驗證

2.1 數據來源

為驗證所提方法的有效性，在C-MAPSS數據集上進行航空發動機RUL預測實驗。該數據集是美國航空航天局預測中心提供的一組C-MAPSS工具模擬產生的由正常運行到失效的過程數據集。該數據集包含4組不同工作環境與不同故障模式下的數據集，包括引擎單元號、時間戳、3種配置以及 21 個傳感器讀取的數據，其中21個傳感器數據和3個工作環境配置參數用來記錄發動機的整個性能退化過程。每個數據集包括訓練集、測試集和RUL預測子集。第1組訓練集數據是在同一種運行環境下發生的單一故障的集合，包含100個發動機的監測樣本，本文選取單一故障模式的第1組數據進行后續實驗。

2.2 關鍵參數選取

根據1.2的分析，選擇FD001中監測數據樣本進行實驗，計算Spearman系數得到如圖1所示的參數變化趨勢結果圖。

圖 1 參數變化趨勢Fig.1 Parameter variation trend

從圖1可以看出，數據集里的21個傳感器參數有常數(Spearman系數為0)、單調增加(Spearman系數為正)與單調減少(Spearman系數為負)3種情況。為便于后續計算，選取擁有單調遞增趨勢的參數，但本文方法不會受到監測數據單調趨勢的影響。符合單調遞增的參數序號為2、3、4、8、11、13、15、17，其趨勢值如表1所示。

2.3 航空發動機RUL預測

由航空發動機的歷史性能退化數據建立考慮三源不確定性的航空發動機性能退化模型。首先，利用Spearman系數對21個監測參數進行篩選。其次，在確定了關鍵參數的基礎上，利用最大熵無跡粒子濾波和ECM算法，進行參數先驗分布的估計。最后，在獲得新的性能退化數據后通過模型參數的在線更新得到參數后驗分布。RUL預測的具體步驟如圖2 所示。

圖 2 RUL預測流程圖Fig.2 Flow chart of remaining useful life time prediction

為驗證所提方法的有效性，選取M1方法進行對比實驗[19]，實驗分為3個方面進行：首先，將本文方法與M1方法分別對航空發動機性能退化數據進行RUL預測，對比2種預測方法的預測精度；然后，使用M1中卡爾曼濾波與ECM算法相結合的模型參數估計方法估計模型的未知參數，分別采用本文模型與M1模型進行航空發動機RUL預測；最后，分別用最大熵無跡粒子濾波與ECM算法相結合的參數估計方法和M1中卡爾曼濾波與ECM算法相結合的參數估計方法對退化模型的未知參數進行估計，使用本文模型作為航發動機的退化模型進行航空發動機RUL預測對比實驗。

M1方法：同時考慮三源不確定性和非線性性，但其假設測量誤差服從正態分布，不能很好地反應測量出現極端值的情況。并且，在參數估計過程中，模型參數一旦確定，就不會再隨退化數據的累積而更新。

為更好地衡量比較結果，本文選取RUL預測領域常用的MSE作為指標，該指標可以很好地表現RUL預測的精度和不確定性，計算公式為

(11)

圖3給出了2種預測方法在航空發動機從出廠到失效的所有觀察點的MSE對比結果。

圖 3 本文方法與M1方法的MSE對比圖Fig.3 MSE comparison between the method in this paper and the M1 method

從圖3可以看出，在25個飛行循環之前本文預測方法的誤差明顯高于M1方法。這是因為，由于本文方法退化模型的初始參數是隨機的，因此在監測初期性能退化數據較少時，本文方法的MSE高于M1。在第25個飛行循環與第60個飛行循環之間，本文預測方法的MSE值與M1方法的MSE值接近。這是因為，隨著飛行循環的增加、監測數據的增多，本文預方法的模型參數自適應更新使模型參數更加貼合實際情況。在過了65個飛行循環之后本文預測方法的預測誤差明顯低于M1預測方法，整體上看，本文預測方法的MSE值為13.25，M1預測方法的MSE值為16.12，說明本文預測方法有更高的預測精度，驗證了它的有效性。

在此基礎上，為驗證所提模型的有效性，在2種模型上均采用M1方法估計未知參數，并進行航空發動機RUL預測，實驗結果如圖4所示。

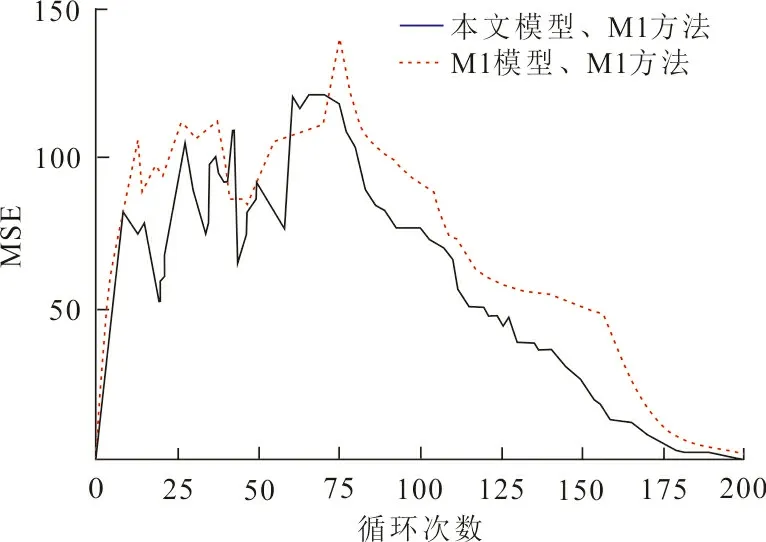
圖 4 方法相同時2種模型的MSE對比圖Fig.4 MSE comparison diagram of the twomodels when the methods are the same

從圖4可以看出，在前10個飛行循環2種模型的預測精度接近，但10個飛行循環之后本文退化模型比M1模型具有更好的預測效果。應注意的是，在75個飛行循環附近，2種模型的預測誤差均出現了上升趨勢，這是因為在75個飛行循環附近，監測數據出現了異常值，影響了預測精度。但本文模型的預測精度高于M1模型的預測精度，說明本文模型能夠有效地減弱監測數據異常值對預測精度的影響。從整體來看，本文模型比M1模型具有更高的預測精度，說明本文模型可以有效提高預測準確性。

接下來，為驗證本文參數估計方法的優越性，采用本文模型作為退化模型，參數估計方法分別采用M1方法和本文方法，實驗結果如圖5所示。

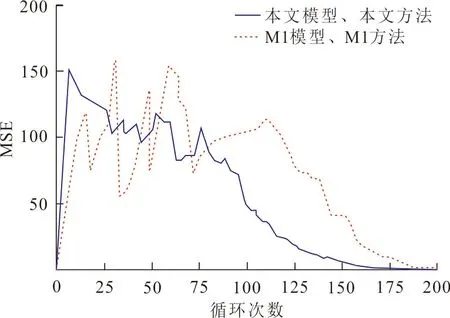
圖 5 模型相同時2種參數估計方法的MSE對比圖Fig.5 MSE comparison diagram of the twoparameter estimation methods when the models are the same

從圖5可以看出，在退化模型相同時，使用本文參數估計方法進行RUL預測，具有更高的預測精度，同時，可看出本文參數估計方法可以提高預測模型的收斂速度和魯棒性。

3 結 語

本文提出了一種考慮三源不確定性的Wiener過程航空發動機RUL預測方法。該方法將三源不確定性引入退化模型,且假設測量誤差服從Logistics分布，能對測量誤差較大的情況進行更好的擬合。在進行航空發動機RUL預測時，使用基于Spearman系數的關鍵參數篩選方法，篩選出對退化過程貢獻更大的參數。然后，將基于最大熵無跡粒子濾波與ECM算法結合估計模型參數。在C-MAPSS數據集上的仿真實驗，證明了該方法可以提高預測的準確性，可以提高航空發動機的使用率和可靠性。航空發動機的退化過程不僅普遍存在三源不確定性和非線性性，還存在多階段的特點，在下一步研究中，應考慮航空發動機退化過程的多階段性。